一种改进的彩色图像去马赛克总变分模型

刘铭丽， 王希云

太原科技大学应用科学学院，山西 太原 030024

去马赛克问题自提出以来得到了人们的广泛关注与研究.杨斌等[1]提出的彩色图像的扩展联合稀疏表示模型，有效地减少了传统模型恢复图像中出现的锯齿现象，但不能很好地保留细节和边界的信息；刘巧珍等人[2]提出的一种基于残差平面超分辨重建的CFA插值方法，有效地保持了图像中的纹理和边缘信息，但容易出现传统插值问题中的锯齿现象；而由Rudin，Osher和Fatemi[3]提出的总变分正则化模型(ROF模型)，由于其正则项具有分段光滑的特性，使得总变分模型能够在图像恢复过程中有效保留图像边缘，从而得到更好的恢复效果，因此这一模型被广泛应用于求解彩色图像的去马赛克问题.

在ROF模型[3]的基础上，Laurent Condat[4]将彩色图像的离散总变分模型表示为

(1)

其中，Ω∈R3n2，A为马赛克算子即彩色滤波阵(选用BayerCFA[5])，a为观察到的马赛克彩色图像.B为离散梯度算子，x为待求彩色图像，μ1>0为正则化参数.文献[4]中，模型的求解算法如下：

其中γ>0,λ>0.

本文考虑到彩色图像三通道融合的情况，选择在传统的总变分模型(1)的基础上引入彩色图像的灰度化项作为正则化项第二项.另外由于亮度色度空间中信息的无关性，将彩色图像由RGB映射到亮度色度空间，利用原始对偶不动点算法(PDFP)在亮度色度空间求解探索彩色图像去马赛克质量的情况.数值实验表明，本文模型比传统模型得到了更好的恢复图像.

1 模型的建立及其求解

传统的彩色图像去马赛克总变分正则化模型，例如模型(1)，仅考虑彩色图像三通道分离的情形，这样忽略了三通道间的相关性，显然会降低图像复原的效果.而彩色图像灰度化的加入将三通道融合的情况考虑进去，因此会达到更好的效果.

1.1 彩色图像的灰度化

灰度化，在RGB模型中，如果R=G=B时，彩色表示一种灰度颜色，其中R=G=B的值叫灰度值，因此，灰度图像每个像素只需一个字节存放灰度值，灰度范围为0～255.一般有分量法、最大值法、平均值法和加权平均法四种方法应用于灰度化彩色图像.其中，平均值法和加权平均法较为常用.

平均值法.将彩色图像中的三分量亮度求平均得到一个灰度值，可以按公式[6]:

加权平均法.根据重要性及其他指标，将R、G、B三个分量以不同的权值进行加权平均,可以得到比较合理的灰度图像.由于人眼对绿色的敏感度最高，对蓝色的敏感度最低，可以按公式[6]:

f(i,j)=0.30×R(i,j)+0.59×G(i,j)+0.11×B(i,j)

1.2 模型的建立

设Sx=f，结合模型(1)可知，本文建立的模型为

(2)

1.3 模型的求解

虽然总变分模型能够有效保留图像边缘，但因其具有非光滑性，直接求解难以获得最小值，而原始对偶不动点算法是求解图像非光滑凸优化问题的一种有效算法，其变量是全分裂的参数范围小，容易选取，因此适用于数量级较大的模型问题.所以本文考虑用原始对偶不动点算法(PDFP)[7,8]求解该模型.

对于目标函数

(3)

利用原始对偶不动点算法[7,8]求解式(3)的步骤如下

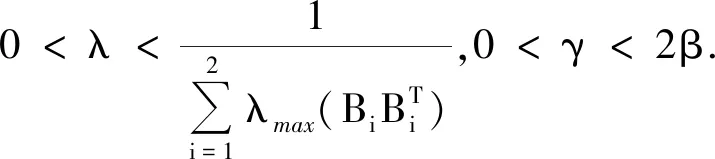
(1)取：

则求解模型(1)的原始对偶不动点算法步骤为

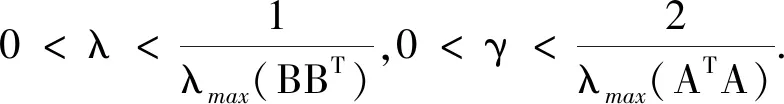
(2)取：

则求解模型(2)的原始对偶不动点算法步骤为

2 数值实验

为了验证本文提出的彩色图像去马赛克模型的有效性，以Matlab2015a为编程工具，实验数据采用7幅像素大小为500×500的彩色柯达图像(Kodak PhotoCD dataset)，分析灰度项参数μ2不同值对实验结果的影响，取μ2∈[0.00,0.11]以0.01为步长，从得到的复原结果中选择最好的结果对应的μ2作为实验最终取值(图1)；对比不同的彩色图像灰度化方法对实验结果的影响(表1)，选取了对实验效果更好的灰度化方法.为了更好地比较去马赛克后的细节信息，且考虑到篇幅影响，用框选出了2幅彩色图像的局部作为实验对比所用的部分(图2)，并选择文献[4]的模型及算法[9]进行对比实验,分别从图像恢复的视觉效果以及峰值信噪比(CPSNR)来主客观地评价所提出模型的性能.

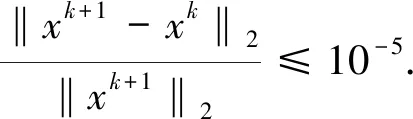
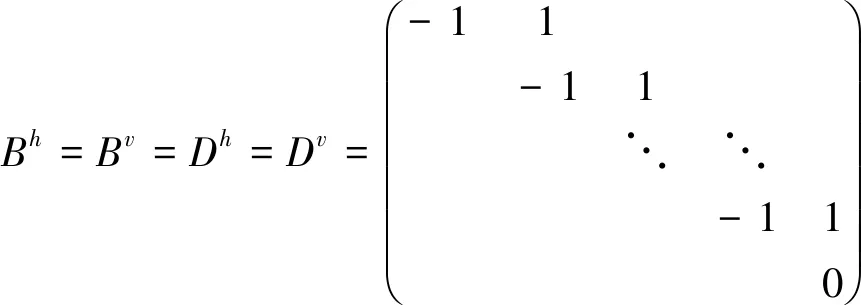
图1 μ2 值对实验结果(CPSNR)的影响Fig.1 The effection on experimental results of the value of μ2表1 不同灰度化方法对实验结果的影响Tab.1 The effection on experimental results of different gray methods

图2 柯达图
Fig.2 kodak image

(a) macaws(b)Windows

图3 实验结果对比图
Fig.3 Collation map of experimental results

主观上，图3中(a)～(b)从左上角到右下角分别为：原图、文献[4]结果图([4])、文献[4]利用PDFP算法结果(下文简称[4]+PDFP)以及本文模型利用PDFP求解结果(下文简称[4]+灰度+PDFP).从图3可以看出文献[4]模型的实验结果出现了色彩失真和边界模糊的现象，由于此模型只考虑了三通道分离的正则化，没有充分利用三通道融合的信息从而使得结果失真.而本文的模型在文献[4]模型的基础上加进去彩色图像的灰度化图像，将三通道融合的信息考虑进去，较好地保留了图像的细节信息，从而使得去马赛克后的图像细节部分更接近原图.并且利用PDFP算法求解文献[4]模型所得图像较文献[4]算法结果更清晰，保留了图像的细节信息.从而说明了此模型和算法的有效性.

客观上，为了检测图片还原质量的好坏，采用峰值信噪比(CPSNR)作为图片质量的评价标准,CPSNR可描述为

表2(黑体表示较好的效果)分别表示文献[4]与本文模型结果的CPSNR值，从表2比较结果可以看出本模型的每幅图像的CPSNR值都比文献[4]高约2 dB.主观和客观评价都显示了本文模型的优越性.

3 结语

本文提出了一种改进的彩色图像去马赛克总变

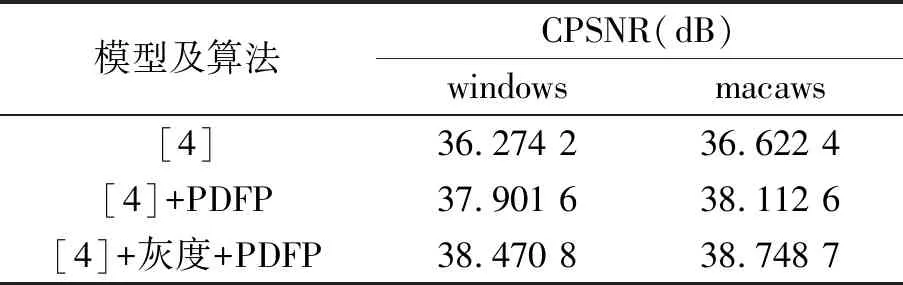
表2 图像恢复结果的信噪比CPSNRTab.2 The CPSNR of image restoration results

分正则化模型.将彩色图像的灰度化图像引入传统模型中，利用原始对偶不动点算法处理该模型.实验结果表明，与文献[4]中的模型相比较，用本文提出的模型恢复的彩色图像有较高的信噪比，能有效地保留图像边缘，提高图像的恢复质量.计算时因矩阵维数大导致对电脑配置要求较高，效率低，因此对本文所用算法还有待改进的地方，比如降维方面的改进，是当前正在进行的研究工作.