弱不可约严格α-对角占优矩阵的表征及应用
邢 峰
1 引言与定义
利用矩阵的对角占优性给出非奇异H-矩阵的判定是许多学者关注的问题,文献[2]-[4]给出了利用Ostrowski定理及连对角占优性判定非奇异H-矩阵的最新成果,文献[1]又利用按环路α-连对角占优矩阵的理论,给出了若干判定非奇异H-矩阵的条件,本文继文献[1]之后,也是利用按环路α-连对角占优矩阵的理论,给出若干实用的判定非奇异H-矩阵的新条件,改进了以往的某些结果,并用实例说明其有效性。
设A=(aij)∈Cn×n是n阶复矩阵,N={1,2,…,n},记
本文用Γ(A)表示A的方向图,用V(A)表示Γ(A)的顶点集合,用C(A)表示Γ(A)中所有非平凡环路的集合,并且约定,若Γ(A)的某个顶点i在环路v中,则记i∈v
本文对任意固定α∈[0,1]还记
VC(A)={i∈V(A)|i∈v∈C(A)}
定义1[1]设A=(aij)∈Cn×n,若V(A)=VC(A),则称A为弱不可约矩阵,记作A∈WI
定义2[1]设A=(aij)∈Cn×n∩WI,若对某α∈[0,1]有C(A)=JC(A),则称为弱不可约严格α-对角占优矩阵,记作:A∈WDα
定义3[1]设A=(aij)∈Cn×n,若|aii|>Pi(∀i∈N),则称A为严格对角占优矩阵,记作A∈D;若存在正对角矩阵X,使AX∈D,则称A为非奇异H-矩阵。记作A∈H。.
当A=(aij)∈Cn×n时,记
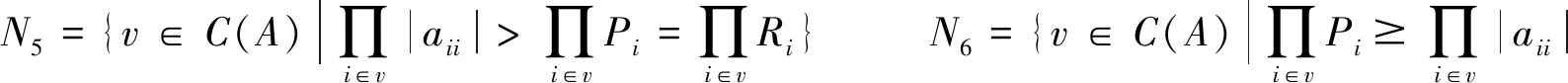
则有C(A)=N1∪N2∪N3∪N4∪N5∪N6
为书写方便,本文特约定

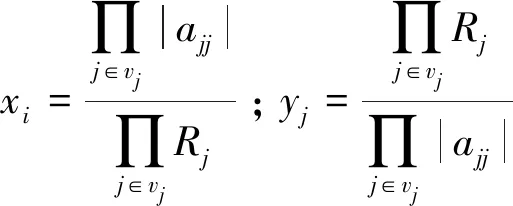
则知αi>1;βi>1;xj>1;yj>1。
2 基本结果
引理1[1]设A=(aij)n×n∈WDα,则A∈H。
定理1 设A=(aij)n×n∩WI,则A∈WDα的充分必要条件为N6=φ,且∀vi∈N1,∀vj∈N2有
logαiβiβi+logxjyjyj<1 ,
(1)
证明 充分性,由(1)式得 logxjyjyj<1-logαiβiβi,
因为αi>1,βi>1,则αiβi>βi,由此知0 则知存在充分小的正数ε,使0 logxjyjyj<1-(logαiβiβi+ε), (2) 令α=logαiβiβi+ε,知0<α<1,且有 α>logαiβiβi, (3) 再由(2)式又有 logxjyjyj<1-α 综上,再由N6=φ知A∈WDα。 必要性,若A∈WDα,则易见N6=φ,且由∀vi∈N1 由此得 logαiβiβi (4) 由此得 logxjyjyj (5) 把(4)和(5)式两端分别相加即得(1)式。 推论1 设A=(aij)n×n∩WI,则A∈WDα的充分必要条件为N6=φ,且∀vi∈N1,∀vj∈N2有 logαiβiαi+logxjyjxj<1 证明 因为∀vi∈N1,∀vj∈N2有以下等式成立 logαiβiαi+logαiβiβi=1 logxjyjxj+logxjyjyj=1 则知logαiβiαi+logxjyjxj<1的充分必要条件为logαiβiβi+logxjyjyj<1 则根据定理1知结论成立。 定理2 设A=(aij)n×n∩WI,N6=φ,若∀vi∈N1,∀vj∈N2有 logαiβiβi+logxjyjyj<1,则A∈H. 证明 由定理1的充分性知A∈WDα,再由引理1知A∈H. 推论2 设A=(aij)n×n∩WI,N6=φ,若∀vi∈N1,∀vj∈N2有 logαiβiαi+logxjyjxj<1 则A∈H。 证明 由推论1知A∈WDα,再由引理1知A∈H。 定理3 设A=(aij)n×n∩WI,若N1∪N6=φ,则A∈H。 证明 若N2≠φ,因为∀vj∈N2,有xj>1;yj>1 则xjyj>xj,故0 (xjyj)α<(xjyj)logxjyjxj=xj 综上知A∈WDα。 若N2=φ,则知C(A)=N3∪N4∪N5,自然有A∈WDα,则A∈H。 定理4 设A=(aij)n×n∩WI,若N2∪N6=φ,则A∈H。 证明 若N1≠φ,因为∀vi∈N1,有αi>1;βi>1,则αiβi>βi,故0 综上知A∈WDα.。 若N1=φ,则知C(A)=N3∪N4∪N5,自然有A∈WDα,则A∈H。 这里|a11|=3,|a22|=2.5,|a33|=2;P1=3,P2=2.5,P3=1.5;R1=3,R2=1.5,R3=2.5 综上知A∈WDα,则由引理1知A∈H。 但文献[1-5]中的一些主要定理却不能判定A是非奇异H-矩阵。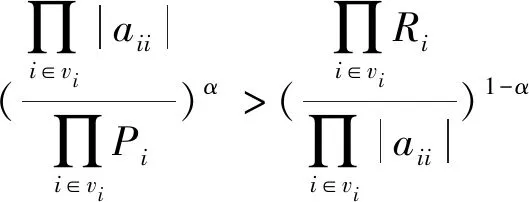

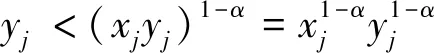









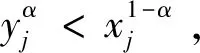
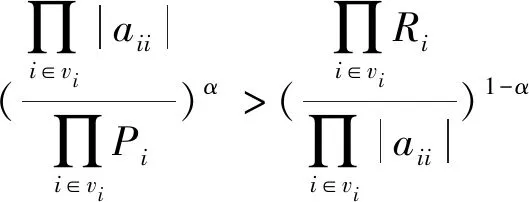



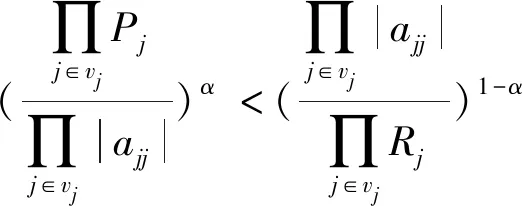
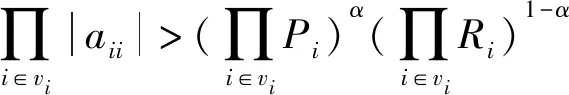

3 数值实例



