借一道真题析全国大学数学竞赛题的教学启示

王成强

全国大学数学竞赛活动每年举办一届，有预赛与决赛之别，每年十月份进行预赛，预赛中表现优异者参与次年举办的决赛[1]。全国大学数学竞赛试题分为数学专业类与非数学专业类，它们的命制角度新颖，趣味性浓郁，创新性充分，能增加大学生学习数学的兴趣，能为数学学习提供有效的课后补充，能丰富学生检视学习效果的手段、为教师提供检验教学效果的手段，能为大学数学试题的设计提供示范。 大学数学竞赛试题的研究对大学数学的学习与授课都有重要的启发性意义。本文旨在以一道竞赛题为例，探析中国大学生数学竞赛题对教学的启示。本文的研究对象是第十届(2018年)大学数学竞赛数学专业类第四题[2]，即

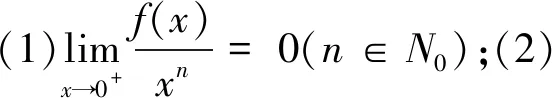
本文拟从“设计特点”、“解法分析”、“教学启示”三方面展开对问题(*)的研究。

1 设计特点研究

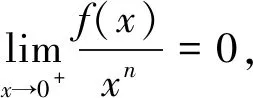
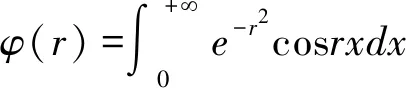
第(1)小问简单，第(2)小问比较复杂，第(1)小问对第(2)小问的解答有一定启发性作用，第(2)小问又依赖于第(1)小问。 总体上，问题(*)难度层层增大，小问题之间关系紧密，共同构成一个“有机”整体，具有高度的统一性与完整性。

2 解法研究

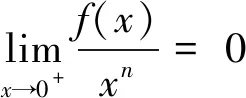
此解法的思路来自于竞赛组委会提供的答案，其解答想法直接且思路简单易懂。

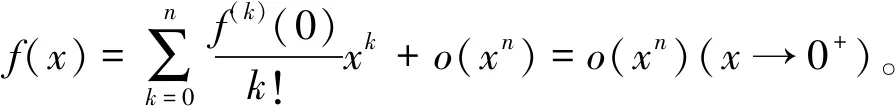
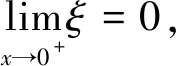
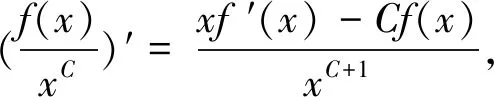
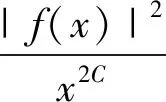
于是当x∈(0,1]时，有|f(x)|2≤0·x2C=0。 又f(0)=0，故在[0,1]上，恒有f(x)=0。

3 教学启示

中国大学生数学竞赛已经举办10届，其办赛宗旨是帮助任课教师提高大学生学习数学的兴趣，帮助高校培养人才、服务教学、促进高等院校数学类课程的教学改革，帮助国家和社会发现、甄别、选拔数学创新人才，为青年学子展示其数学能力的舞台[5]，经研究发现，中国大学生数学竞赛在这些方向已经取得了不错的成效[6-9]。 非数学专业类试题主要考察应试者对微积分理论知识的掌握，数学专业类试题由高等代数、数学分析、解析几何三大知识模块构成，这些试题对大学数学类课程(如数学专业的高等代数、数学分析、解析几何等课程)的教学有重要的启示。

3.1 大学数学教学要重视数学思想方法的渗透

“授之以鱼，不如授之以渔”。 学习数学的最主要目的是借其解决数学问题。 因此，大学数学的教学既要重视概念、性质、典型例题、解题技巧等的讲授，也要重视渗透理解数学概念、性质的多种视角的思想，重视渗透发现处理数学问题方法的思想，重视渗透数学技巧背后隐藏着的数学本质。

数学思想的渗透，要以具体的数学问题为背景。课程教学过程中，教师切忌脱离实例传授数学思想，而是在理论知识讲授或者例题示范的过程中，将课前精心准备好的问题审题、问题分析与问题解答展示给学生，将无形的思想寓于有形的具体问题与其解答过程中，让学生更具象地感知到问题中蕴藏着的数学思想。 例如，在验证满足问题(*)条件的函数f(x)在区间(0,1]上总成立着f(x)=0的过程中，用到了“为验证函数f(x)≡0可微可通过验证m(x)f(x)≡0，其中m(x)恒不为零”“为验证非负函数m(x)f(x)≡0可通过验证supm(x)f(x)≡0”“为确定出supm(x)f(x)可通过对函数m(x)f(x)求导、找出单调区间加以完成”。 这些思想仅凭语言极难描述，只有通过思索问题(*)的解答或阅读问题(*)的解题过程，并结合自己的解题经验，心才能有所得；这些思想对学生的数学学习大有裨益，能帮助学生强化活用“为验证f(x)≡0可通过验证f′(x)≡0且fmax≡0来完成”这一思想的意识。

数学思想的渗透，要结合教材知识体系安排来开展。数学类课程教材的编著者一般是教学科研经验丰富的相关邻域的专家，他们会有意识地将数学思想科学合理地“寄存”在教材的例题、课后习题等内容中。 数学教师课前要认真把握教材，课程教学中要引领学生在适当的时间、在正确的“地点”将“寄存”好的思想“取走”。 教师在什么时候、什么知识模块渗透什么数学思想，应最大程度地遵照教材的先后顺序。 教师在备课阶段不要漏掉教材中的数学思想，在课程教学中不要随意发挥、更不要试图集中讲完所有数学思想。 做到这几点，教材就会得到充分利用，学生就会在感知到一种数学思想之后，通过动手做题，加深对此数学思想的认识，并为感知并接受下一种数学思想做好准备。在给定的课时内，教师引领学生“取”完所有的数学思想，这就意味着该门课程的教学任务的完成。

数学思想的渗透，可结合真实的数学历史趣闻。数学思想的感知活动也曾真实地发生在许多数学家身上，结合发生在数学家身上的真实故事渗透数学思想，教师通过其语言描述，让学生“置身”于数学历史人物与数学历史情景中，引导学生了解一种数学思想的产生背景、产生过程以及它的局限性，帮助学生加深对该数学思想的认识。

数学思想的渗透，要调动学生的主观能动性与课堂参与的热情。数学思想无形，学生只有与授课教师共同参与问题的阅读、分析、解答等全过程，通过师生之间思想的沟通，学生才能对其有所感知。数学思想无形，只有通过适量的随堂练习与充分的课后练习加深对其的认识。因此，教师需要激发学生的课堂参与的热情以确保学生感知到数学思想，需要调动学生的主观能动性以确保学生真正地掌握数学思想。

3.2 大学数学教学要重视培养学生的数学能力

大学数学的教学在帮助学生构建数学知识体系的同时，也要重视帮助学生养成从问题出发(结合已知条件)寻找解决关注问题的思路与线索的能力。一般地，数学能力包括逻辑推理能力、科学计算能力、转化划归能力、抽象思维能力等。

数学能力的培养，要遵循循序渐进的原则。数学能力的养成不能一蹴而就，是靠学生经过大量习题训练之后逐渐积累的，任课教师要遵循事物发展的规律，在适当地时候帮助学生提升特定的数学能力，切勿操之过急。例如，在学习L’Hpital法则阶段，就要求学生掌握正确运用L’Hpital法则验证极限恒等式的能力，在学习Taylor多项式理论阶段，就要求学生掌握正确借助于Taylor多项式验证极限恒等式的能力，在期末复习或考研复习阶段，就要求学生掌握正确运用L’Hpital法则和借助于Taylor多项式验证极限恒等式的能力。

数学能力的培养，要采用科学合理的课程学习评价方式。为动态监测学生数学能力的提升，科学合理的课程学习评价方式应既要注重过程性评价，又要重视课程考试的卷面成绩所反映出的数学应试能力。 现目前各高校普遍采用的一种评价方式是将平时表现所得成绩与期末卷面成绩的加权平均作为学生课程学习的综合评价成绩。此法比较省事，顾及到了过程性评价，兼具学生的课程学习的定性评判与定量分数，它是一种科学合理的课程学习评价方法。诸如高等代数、解析几何、数学分析等课程的平时表现所得成绩可适当考虑学生在数学竞赛等活动中的表现，这有助于更多地体现对学生数学能力的评价。

3.3 大学数学教学要重视培养学生的创新意识与热爱探索的品质

接受大学数学教育，是为大学毕业之后的工作和学习中的科研做准备。科研需要参与者的创新意识与热爱探索的品质。事实上，创新意识与热爱探索的品质在解答数学问题中也必不可少，例如，在问题(*)中，从学习微分方程xf′(x)=Cf(x)的经验中探索出，需要在分不等式|xf′(x)≤C|f(x)|的两端同时乘以x-C-1，换言之，在这里就将常微分方程的积分因子法创新地用到了微分不等式中。

数学创新意识与热爱探索数学的品质表现为热爱做数学题、喜好挑战高难度数学题、热衷于对一道数学题给出多种求解策略、喜欢参与课堂学习等。为培养大学生的数学创新意识与热爱探索数学的品质，任课教师在教授课程时要随时关注学生的数学创新意识与热爱探索数学的品质的表现，给学生正反馈，逐步培养出学生的创新意识与热爱探索的品质。

3.4 大学数学教学要重视引导学生感受到数学蕴藏的趣味性

大学数学规定要完成的学习内容多，课程教学时间又十分有限，参与课程的学生的数学基础还参差不齐，大学学习相较中小学学习的氛围较宽松，所有这些都要求大学数学课程的教学需要充满趣味性，俗话说，“兴趣是成功之母”，只有课堂气氛活跃、数学蕴藏的趣味性展示在学生面前，才能激发学生学习数学的主观能动性，进而才能保质保量地完成教学任务。大学数学的任课教师可借助于大学生数学竞赛题目帮助其增强课堂的趣味性。大学生数学竞赛题趣味性浓郁，它们虽源于书本，但难度远超出书本难度，容易引起学生挑战的意愿。

4 结 语

本文从设计特点、解法分析、教学启示三个视角研究了第十届(2018年)全国大学生数学竞赛数学专业类预赛第四题〔即问题(*)〕，并基于此给出中国大学生数学竞赛试题对大学数学教学的启示。 经研究发现该题来源于教材而高于教材，能力立意突出，趣味性浓郁。从解法的研究过程中觉察到，该题难度层层增大，各小问之间相互依赖，具有高度的统一性与完整性。从研究设计特点与解法分析的过程得到四点启示：大学数学教学要重视数学思想方法的渗透、要重视培养学生的数学能力、要重视培养学生的创新意识与热爱探索的品质、要重视引导学生感受到数学蕴藏的趣味性。