分形空间中的广义预不变凸函数与相关的Hermite-Hadamard型积分不等式
孙文兵
(邵阳学院理学院,湖南邵阳422000)
函数凸性在经济数学、管理科学、工程和优化等领域有非常重要的应用。目前,很多学者展开了对函数凸性推广的研究。WEIR等[1-2]提出了预不变凸函数的定义:
定义 1设A⊆Rn,若存在一个向量函数η:Rn×Rn→Rn,对任意x,y∈A,0≤λ≤ 1,有
则称A是不变凸集。
定义2设A⊆Rn是一个关于η:Rn×Rn→Rn的不变凸集。f:A→R是一个函数。若对任意x,y∈A,0≤λ≤ 1,有

则称函数f是预不变凸的。
显然,当式(1)中,取η(x,y)=x-y时,f便是一个凸函数,因此凸函数是一个关于η(x,y)=x-y的预不变凸函数,而预不变凸函数是凸函数的一种推广。关于预不变凸函数的性质,可参阅文献[3-4]。
Hermite-Hadamard不等式的推广研究是与函数凸性紧密相关的,该不等式叙述如下:
令f:I⊆R→R是一个凸函数,其中a,b∈I,a<b,则

如果f是凹的,则不等式反号。根据不同的凸性定义,涌现了许多Hermite-Hadamard不等式的新研究结果[5-8]。自提出预不变凸函数定义以来,相继出现了Hermite-Hadamard不等式与预不变凸函数相关的研究[9-12]。NOOR[9]证明了关于预不变凸函数的Hermite-Hadamard不等式。
定理1令f:K=[a,a+η(b,a)]→(0,∞)是区间K∘上的一个预不变凸函数(K∘是K的内部),a,b∈K∘且a<a+η(b,a)。则有
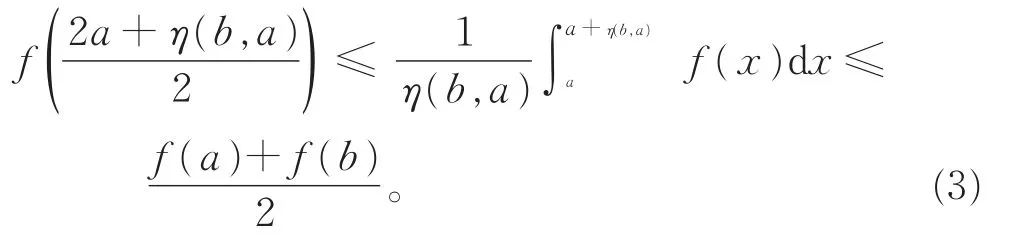
注1若η(x,y)=x-y,不等式(3)变成了不等式(2),即不等式(3)是经典的Hermite-Hadamard不等式的推广。
BARANI等[10]推广了函数导数绝对值是预不变凸函数的Hermite-Hadamard型积分不等式,得到:
定理 2设A⊆R是一个关于θ:A×A→R的开的不变凸集,f:A→R是一个可微函数。如果|f′|在A上是预不变凸的,那么对每一个a,b∈A且θ(b,a)≠ 0,有
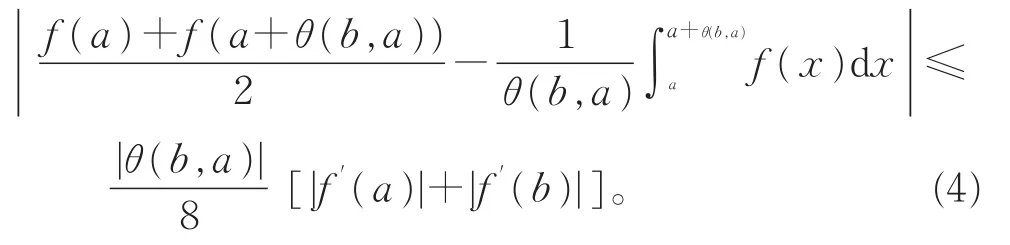
定理3设A⊆R是一个关于θ:A×A→R的开的不变凸集,f:A→R是一个可微函数。假设p∈R且p> 1,如果|f′|p/(p-1)在A上是预不变凸的,那么对每一个a,b∈A且θ(b,a)≠0,有

近年来,分形理论广受关注,因为许多微积分方程描述的物理现象往往涉及一些连续不可微函数,而经典微积分并不能处理这类函数,此类函数被称为分形曲线。于是,越来越多的研究者将所研究的问题推广到分形空间。YANG等[13-14]系统阐述了一种分形集理论并定义了该空间中的分形微积分,称为局部分数阶微积分。MO等[15-16]根据这一理论将函数经典凸性和S-凸函性推广到分形空间并证明了分形空间中的广义Hermite-Hadamard不等式。
定义 3[15]设f:I⊆R→Rα,对任意x1,x2∈I且λ∈[0,1],若有
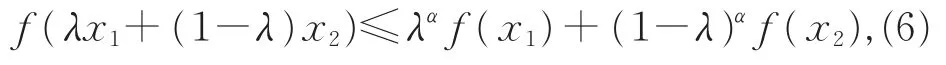
则称f为定义在I上的广义凸函数(不等号反向,则称f为广义凹函数)。
定理 4[15]令f(x)∈I(α)x[a,b]为区间[a,b]上的一个广义凸函数,a<b,则
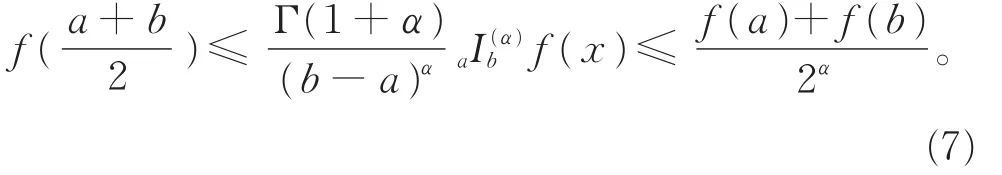
文献[17]提出了分形空间Rα(0<α≤1)中的广义调和凸函数的定义,并证明了相关的Hermite-Hadamard型不等式。关于分形空间中积分不等式的一些新研究结果可参阅文献[18-22]等。
在YANG提出的分形集理论以及局部分数阶微积分理论基础上,本文提出了分形空间上广义预不变凸函数的定义,并建立了与广义预不变凸函数相关的Hermite-Hadamard型积分不等式。文中所得推广了文献[9-10]中的一些结果。
1 预备知识
根据YANG的分形集理论,令Rα(0<α≤1)为分形实线的α型集合,是一个维数为α维的分形集,其运算律规定义如下[13]:
若aα,bα,cα∈Rα,则
(a)aα+bα∈Rα,aαbα∈Rα,
(b)aα+bα=bα+aα=(a+b)α=(b+a)α,
(c)aα+(bα+cα)=(a+b)α+cα,
(d)aαbα=bαaα=(ab)α=(ba)α,
(e)aα(bαcα)=(aαbα)cα,
(f)aα(bα+cα)=aαbα+aαcα,
(g)aα+0α=0α+aα=aα且aα1α=1αaα=aα,
(h)|aα|-|bα|≤ |aα+bα|≤ |aα|+|bα|,
(I)(a-b)α=aα-bα。
引理1[13]
局部分数阶导数和局部分数阶积分的定义可参阅文献[13],文献[15-22]中也有介绍,此处只介绍下文将要用到的几个记号:
(1)f(x)在区间[a,b]上局部分数阶连续,记为f(x)∈Cα[a,b];
(2)f(x)在区间[a,b]上α阶局部分数阶可导,记为f(x)∈Dα[a,b];
(3)对f(x)在区间[a,b]上α阶局部分数阶积分 ,记 为aI(α)bf(x)。 若 对 任 意x∈[a,b],有aI(α)xf(x)存在,则记为f(x)∈I(α)x[a,b]。
引理2[13]
(1) 若f(x)=g(α)(x)∈Cα[a,b],则

(2) 若f(x),g(x)∈Dα[a,b],且f(α)(x),g(α)(x)∈Cα[a,b],则

引理3[13]

引理4[13](广义Hölder不等式)令,则
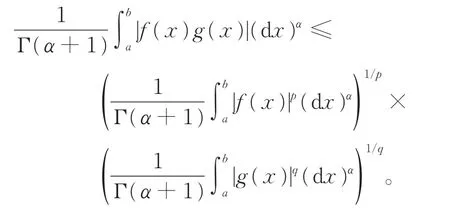
2 主要结果
下面给出分形空间Rα(0<α≤1)中广义预不变凸函数的定义。
定义4设A⊆Rn是一个关于η:Rn×Rn→Rn的不变凸集。f:A→Rα是一个函数。若对任意x,y∈A,0≤λ≤ 1,有

则称函数f是关于η的广义预不变凸函数。函数f是广义预不变凹函数当且仅当-f是广义预不变凸函数。
注 2在式(8)中,当η(x,y)=x-y时,f便是一个广义凸函数(定义3),因此广义凸函数是一个关于η(x,y)=x-y的广义预不变凸函数,而广义预不变凸函数就是广义凸函数的推广。
下面关于双重函数η(·,·)的讨论中,需要给出以下假设[4]:
条件C令I⊂R是一个不变凸集,对任意的x,y∈I,t∈[0,1],双重函数η(·, ·)满足

注 3对每个x,y∈I,t1,t2∈[0,1],由条件C,有η(y+t2η(x,y),y+t1η(x,y))=(t2-t1)η(x,y)。
定理5(广义预不变凸函数的Hermite-Hadamard不等式)令f:K=[a,a+η(b,a)]→Rα(α∈(0,1]),是区间K∘上的一个广义预不变凸函数(K∘是K的内部)且a,b∈K∘,a<a+η(b,a)。若f(x)∈I(α)x[a,a+η(b,a)],双 重 函 数η(·, ·)满 足条件C,则

证明由f:K=[a,a+η(b,a)]→Rα是区间K∘上的一个广义预不变凸函数,在不等式(8)中,取λ=则对所有的x,y∈K∘,有

令x=a+tη(b,a),y=a+(1-t)η(b,a), 并代入上式,可得
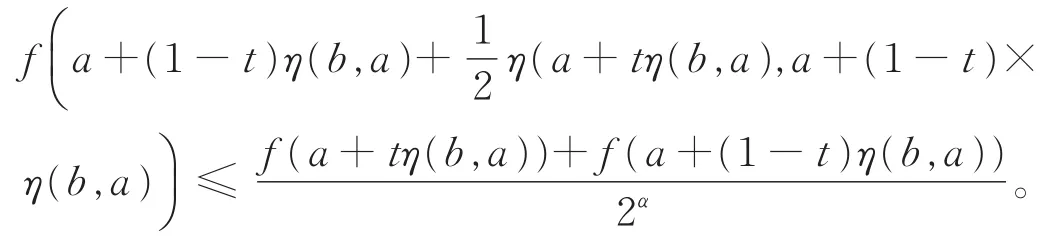
由条件C的注3,有
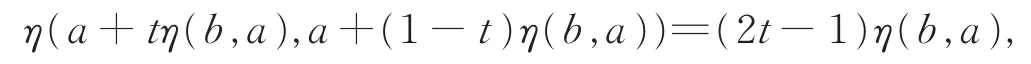
于是由上式可得

上式两边对t在[0,1]上局部分数阶积分,可得
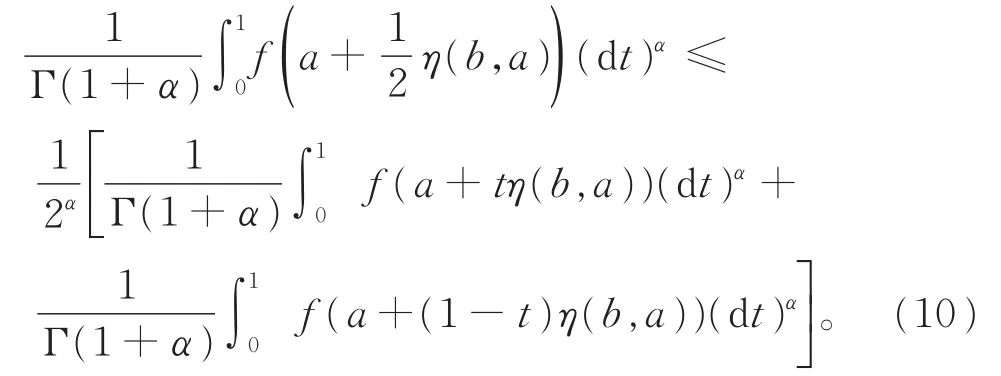
由引理3和引理1,有
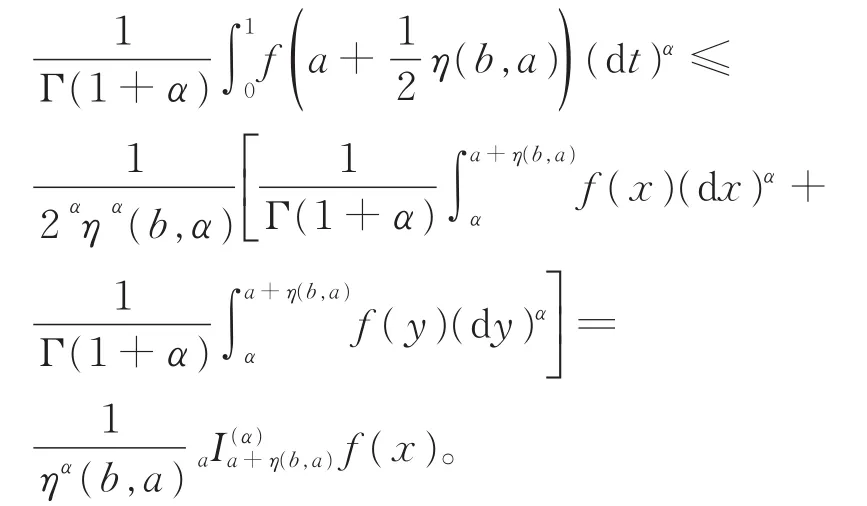
另一方面,
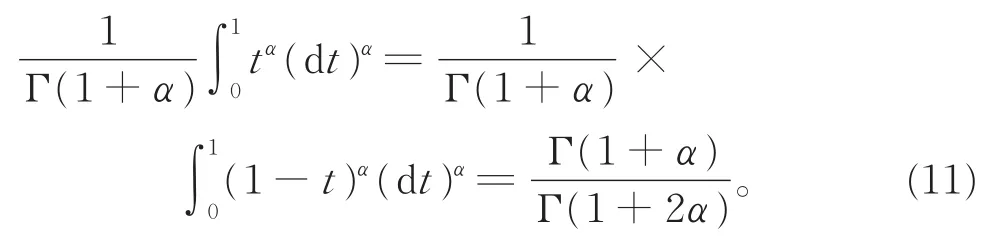
由于f是一个广义预不变凸函数,令x=a+tη(b,a),t∈[0,1],由式(11),有

由式(10)和(12),可知定理成立。证毕。
注4 定理 5中,取α=1,则由不等式 (9)可得不等式(3)。
推论 1定理 5中,取η(b,a)=b-a且a<b,有以下类似于定理4的局部分数阶积分不等式:

注5推论1中,取α=1,则由不等式 (13)也可得到经典的Hermite-Hadamard不等式(2)。
引理 5令I⊆R是关于η:I×I→R的一个开的不变凸集,a,b∈I,η(b,a)≠ 0。如果f:I→Rα(α∈(0,1])使 得f∈Dα(I)且f(α)(x)在η- 路 径Pav,v=a+η(b,a)上局部分数阶可积,则
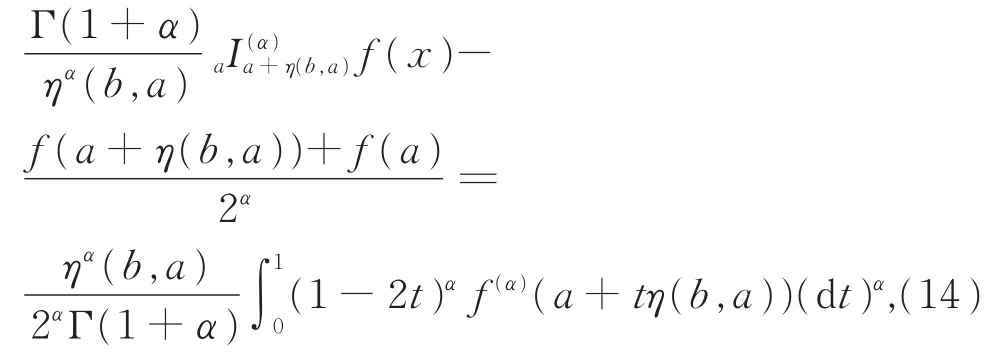
其中,η-路径Pav:={z|z=a+tη(b,a),t∈[0,1]}是连接a与v=a+η(b,a)之间的路径[10]。
证明设a,b∈I,因为I是关于η的不变凸集,对每一个t∈[0,1],有a+tη(b,a)∈I。由局部分数阶分部积分,可得

其中用到换元x=a+tη(b,a)。证毕。
定理 6令I⊆R是关于η:I×I→R的一个开 的 不 变 凸 集。如果f:I→Rα(α∈(0,1])使得f∈Dα(I) 且f(α)∈Cα[a,a+η(b,a)], 其中a,b∈I,a<a+η(b,a);|f(α)| 在区间 [a,a+η(b,a)]上是广义预不变凸函数。则对所有的x∈[a,a+η(b,a)],有

证明设a,b∈I,因为I是关于η的不变凸集,对每一个t∈[0,1],有a+tη(b,a)∈I。式(14)两边取模,由 |f(α)|在区间[a,a+η(b,a)]上是广义预不变凸函数,则有
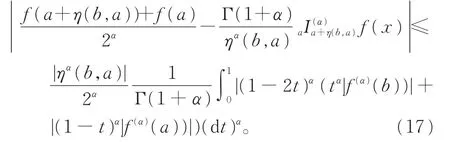
由分形集中元素运算律(I)以及引理3,有
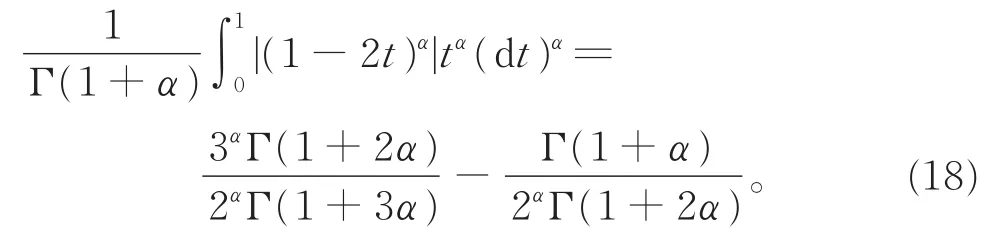
同理可得
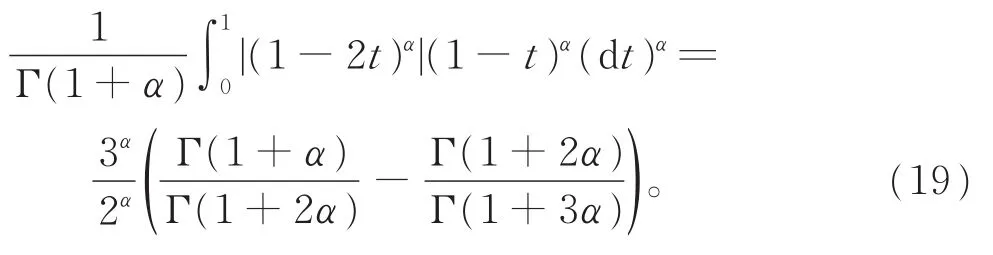
将式(18)、(19)代入式(17),可得式 (16),定理得证。
注 6定理6中,取α=1,则由不等式(16)可得到定理2中的不等式(4)。
推论2定理6中 ,取η(b,a)=b-a且a<b,则有
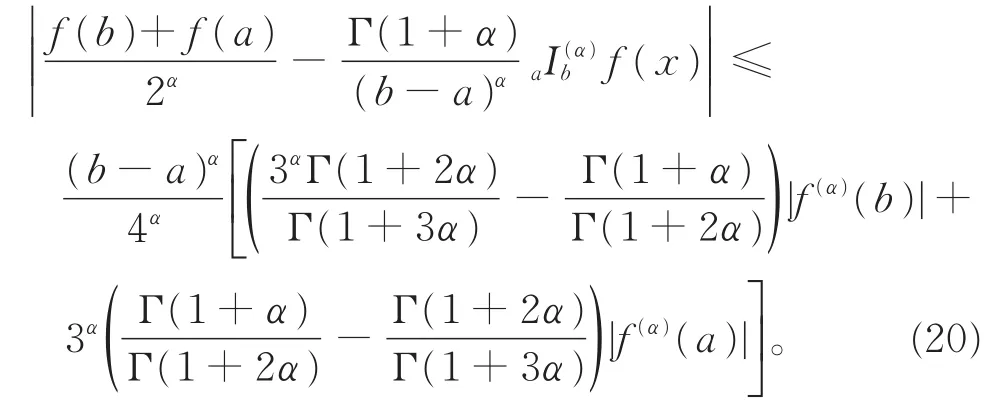
定理 7令I⊆R是关于η:I×I→R的一个开的不变凸集 。 如果f:I→Rα(α∈(0,1])使 得f∈Dα(I)且f(α)∈Cα[a,a+η(b,a)],其中a,b∈I在区间[a,a+η(b,a)]上是广义预不变凸函数,其中p>1。则对所有的x∈[a,a+η(b,a)],有

证明设a,b∈I,等式(14)两边取模,由广义Hölder不等式,有

由引理3,计算可得
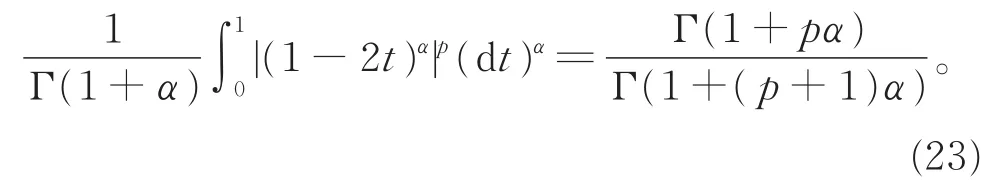

将式 (23)、(24)代入式(22),可得不等式(21),定理得证。
注7定理7中,取α=1,则由不等式 (21)可得定理3中的不等式(5)。
推论3定理7中,取η(b,a)=b-a且a<b,则有
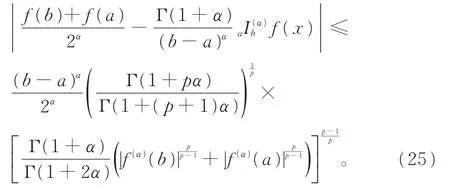
定理 8令I⊆R是关于η:I×I→R的一个开的不变凸集。如果f:I→Rα(α∈(0,1])使得f∈Dα(I)且f(α)∈Cα[a,a+η(b,a)], 其中a,b∈I,a<a+η(b,a);|f(α)|q在区间[a,a+η(b,a)]上是广义预不变凸函数,其中q≥1。则对所有的x∈[a,a+η(b,a)],有
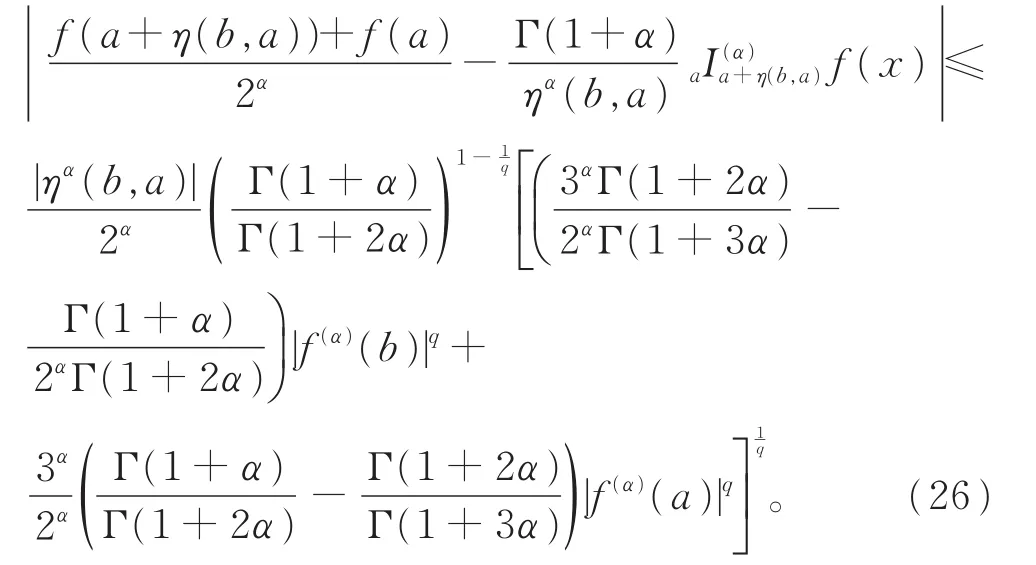
证明设a,b∈I,式(14)两边取模,由广义幂均不等式[23]以及 |f(α)|q在区间 [a,a+η(b,a)]上是广义预不变凸函数,可得
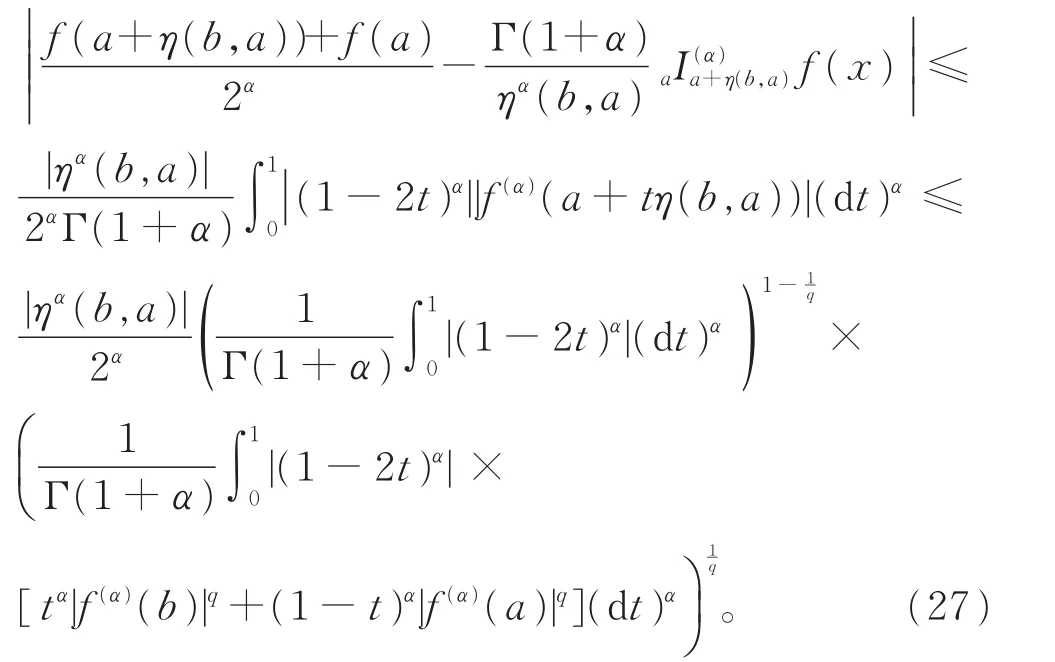
由引理3,经计算可得

将式(18)、(19)、(28)代入式(27),可得不等式(26),定理得证。
注 8定理8中,取q=1,则由不等式(26)可得到定理6中的不等式(16),因此定理8又是定理6的推广。
推论4定理 8中,取η(b,a)=b-a且a<b,则有

推论5定理 8中,取α=1,则由不等式(26),有
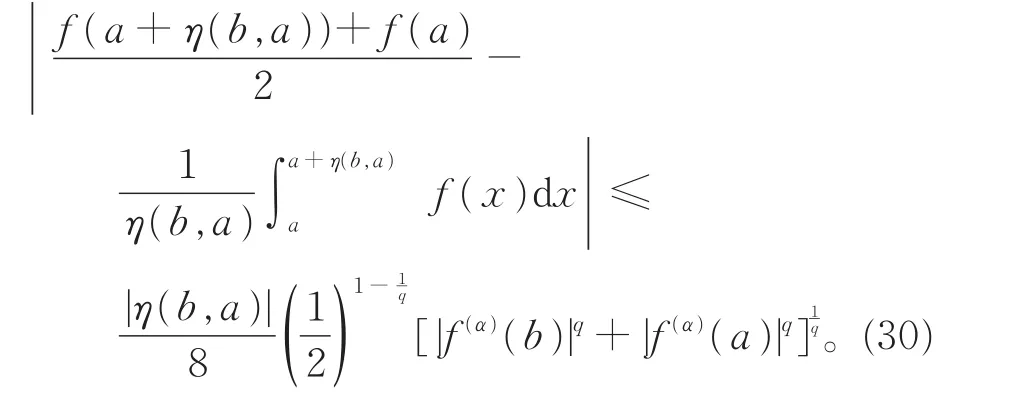
注 9推论5中,取q=1,则由不等式(30)可得到定理2中的不等式(4)。

