二元体相分离模型的静态分歧

闫东明

（浙江财经大学数据科学学院，浙江杭州310018）

0 引 言

一个具有A和B2种组元的复合物质称为二元体，如溶液合金、聚合物等。当二元体冷却到一定温度后可能发生相分离，即原来浓度均匀分布的A和B出现不均匀分布。为了研究二元体合金系统在三相点处的相分离现象，CAHN等[1]导出了如下形式的Cahn-Hilliard/Allen-Cahn偏微分方程组（记为CH/AC)：

其中，未知函数u是一个守恒量，表示一种组元的浓度，v是一个序参数。此外，h是一个代表晶格间距的正参数，α代表相图中的系统位置。Δ是拉普拉斯算子，Ω⊂Rn(1≤n≤3)是有界区域,并且式(1)是一个包含 Cahn-Hillard方程和Allen-Cahn方程的耦合系统。显然，当u=1/2时式(1)退化为Allen-Cahn方程；当v=0时式(1)退化为Cahn-Hillard方程。对于Allen-Cahn方程以及Cahn-Hillard方程，无论是适定性还是稳定性，学者们均做了广泛研究[2-7,12-13]。特别是MA等[12-13]对Cahn-Hillard方程的分歧做了深入研究，得到了Cahn-Hillard方程有吸引子分歧存在的结果。

对二元体合金相分离现象的CH/AC模型研究已取得一些进展。BROCHET等[8]得到了CH/AC系统最大吸引子的存在性。NOVICK-COHEN[9]研究了CH/AC系统的长时间渐近行为。GOKIELI等[10]研究了约束条件下的 CH/AC系统，获得了CH/AC系统全局吸引子的存在性，并证明了初始值ω-极限集的任何元素均为CH/AC系统相应静态问题的解。GOKIELI等[11]给出了一种求解CH/AC系统的数值方法，并给出了CH/AC系统相应静态问题解的数值模拟图像，这些数值模拟结果为理解和研究二元体合金相分离现象提供了直观认识。对于具有更一般非线性项的CH/AC系统，即具有梯度流结构的演化方程，闫东明[14]给出了一些适定性和稳定性的结果。

对CH/AC系统的理论和数值研究均取得了重要进展。然而，这些研究对诸如二元体何时发生相分离、影响二元体相分离的因素有哪些等问题均未给出很好的回答。本文试图通过对CH/AC系统静态分歧的研究，就上述问题给出一些回答。

研究如下问题：

其中，h,α＞0如式(1)所示，Δ是拉普拉斯算子，Ω⊂Rn(1≤n≤3)是有界区域。研究当参数λ变化时的分歧情况。

运用非线性分歧理论以及零指标Fredholm算子的相关性质，证明了二元体相分离模型的静态方程(2)当参数λ超过某个临界值时有分歧发生，即该方程从平凡解(u,v)=(1/2,0)分歧出非平凡解，意味着2种物质的均匀分布状态失去稳定，达到另一种非均匀分布的平衡态，此时对应的二元体有相分离现象发生。另外，得到的临界值与代表晶格间距的正参数h与该模型线性问题第一特征值有关，意味着影响二元体相分离现象发生的主要因素有晶格间距以及二元体所在的区域大小及其形状。更进一步的分析表明，晶格间距越小或者二元体所在区域直径越大，二元体越容易发生相分离现象。

1 预备知识及引理

本文工作空间如下：

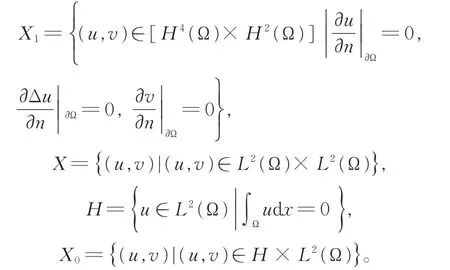
首先，考虑式(2)在平凡解(u,v)=(1/2,0)处的线性特征值问题，即

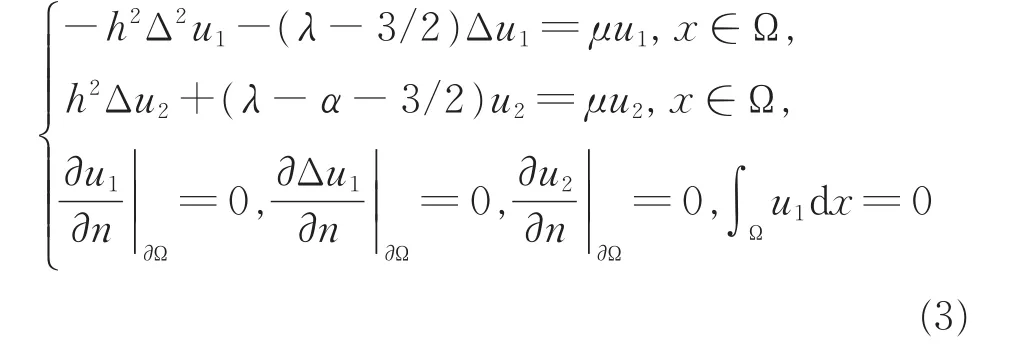
的特征值和特征函数。

令ρk和ek是

的特征值和特征函数，则有

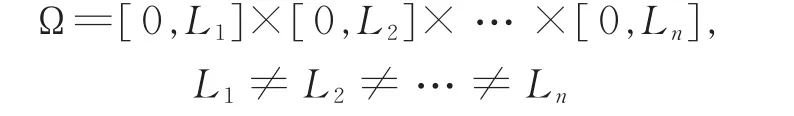
时，式(4)的特征值和特征函数为

其中，

对于线性特征值问题(3)，有以下引理：

引理1若线性特征值问题(3)的特征值为(λ)(j=1,2,k=1,2,…)，则(λ)是 实 的 ，且满足

其中λ0=h2ρ1+3/2。 并且，特征值(λ)对应的特征函数为

其中ek如式(4)所示。

注1由线性稳定性理论，引理1意味着当λ＜h2ρ1+3/2时，式(1)的平衡态(u,v)=(1/2,0)是稳定的，即对初始值的任何小扰动,系统 (1)随时间的演化最终回到平衡态(u,v)=(1/2,0)，此时二元体仍然处于2种物质均匀分布的状态；当λ＞h2ρ1+3/2时，式 (1)的平衡态(u,v)=(1/2,0)是不稳定的，即对初始值的任何小扰动，系统(1)随时间的演化到达异于(u,v)=(1/2,0)的另一个平衡态，该平衡态是静态方程(2)的非平凡解，此时二元体有相分离现象发生。

证明设μ是式(3)的特征值，且其对应的特征函数为(u1,u2)。由 Fourier级数展开，存在 {an}和{bn}，使得

将式(8)代入式(3)，方程两边乘以ek，并在区域Ω上积分，可得

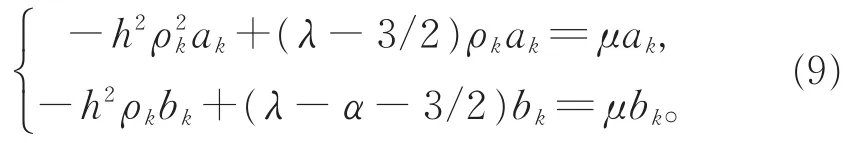
令Mk(λ)矩阵为

则式(9)等价于：

因此 ，式 (3)的特征值μ:=(λ)(j=1,2,k=1,2,…)由矩阵Mk(λ)的特征值给出，即

其对应的特征函数为

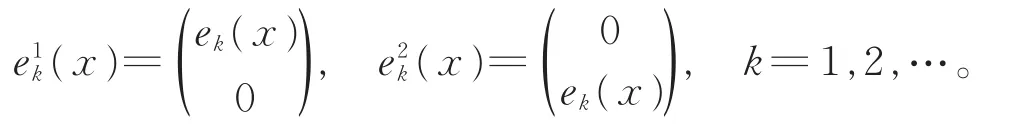
由式(10)易得引理其他结论。引理1证毕。

下面给出一个关于参数化非线性算子方程解集结构的结果。此结果是本文将要用到的主要研究工具。

假设X1,X0为Banach空间。令F:X1×R→X0为非线性可微映射，考虑抽象方程

在参数λ变化时的分歧。以下用N(L)和R(L)分别表示线性算子L的核空间和值域空间；FU表示F关于U的 Fréchet偏导,FλU表示F关于U和λ的Fréchet混合偏导。

引理2[15]令V是X1×R的连通开子集，(U0,λ)∈V，F:V→X0是连续可微映射。假设以下条件成立：

（i）F(U0,λ)=0, (U0,λ)∈V。

（ii）FλU(U,λ)存在，且在 (U0,λ0)关于 (U,λ)连续。

（iii）FU(U0,λ0)是零指标 Fredholm 算子，且dimN(FU(U0,λ0))=1。

（iv）FλU(U0,λ0)[ω0]∉R(FU(U0,λ0)), 其 中ω0∈X0，且N(FU(U0,λ0))=span{ω0}。

令Z是span{ω0}在X0中的补空间。则存在开区间I1=(-ε,ε)以及连续函λ:I1→R,h:I1→Z,使得λ(0)=λ0,h(0)=0,如果对s∈I1有

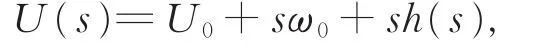
则F(U(s),λ(s))=0,并且在(U0,λ0)附近F-1{0}由曲线U=U0和Γ={(U(s),λ(s)):s∈I1}组成。

2 主要结果及证明

本节将运用引理2进一步研究当参数λ变化时的式(2)的分歧情况。

定理 1假设式(5)中的ρ1是简单的，其对应的特征函数为e1。则方程(2)在(u,v,λ)=(1/2,0,h2ρ1+3/2)附近有唯一的单参数非平凡解簇：

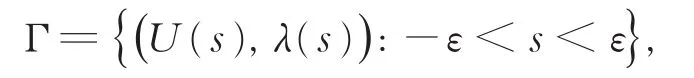
即存在ε以及从 (-ε,ε)到X1×R的C∞函数s↦ (U(s),λ(s))满足

其中h1(0)=h2(0)=0。

注2当二元体所在区域为长方体时，即当

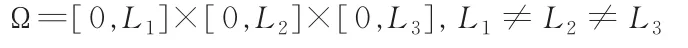
时，由式(7)易见第一特征值ρ1是简单的，条件是自动满足的，这意味着ρ1的简单条件在实验中易被实现。

注3线性稳定性分析指出：当λ＞h2ρ1+3/2时，式(2)有非平凡解存在的可能性。定理1进一步说明式(2)的确有非平凡解存在，并且还给出了该非平凡解的具体表达式式(12)。当Ω为一维区间时，由非平凡解的具体表达式得到的二元体物质分布的图像和文献[11]数值模拟得到的图像是一致的。这意味着定理1很好地回答了二元体什么时候发生相分离的问题，并且还给出了二元体相分离后的具体状态。

注4条件λ＞h2ρ1+3/2中涉及的值h与晶格间距有关，而ρ1与二元体所在的区域大小及其形状有关，且与区域直径成反比。由此可知，影响二元体相分离的主要因素为晶格间距和二元体所在的区域。进一步，由定理1以及条件λ＞h2ρ1+3/2知，h越小，式(2)越容易发生分歧，ρ1越小，式(2)越容易发生分歧，这意味着晶格间距越小或者二元体所在区域直径越大，二元体越容易发生相分离。

证明定义非线性映射F:X1×R→X0×R：

则式(2)等价于

显然，F(1/2,0,λ)=0，并且F是连续可微的，即满足引理2中条件(i)。下面分2步验证引理2中其他条件成立。

第1步证明FU(1/2,0,h2ρ1+3/2)是零指标的Fredholm算子，并且

其中U=(u,v)。

直接计算可得

定义算子B,C:X1→X0×R：

则有

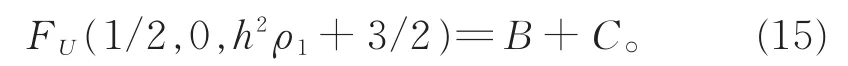
易见C:X1→X0×R是线性紧算子。由紧扰动不会改变Fredholm算子指标的事实，以下只需证明B:X1→X0×R是零指标的Fredholm算子。

易证B:X1→X×{0}是零指标的Fredholm算子。事实上，令D,E:X1→X×{0}为：

则有

易见D:X1→X×{0}是可逆算子，其逆为D-1:X×{0}→X1。式(16)两边同乘D-1，可得

显然

是恒等算子。由椭圆算子的正则性估计以及Sobolev空间紧嵌入定理，有

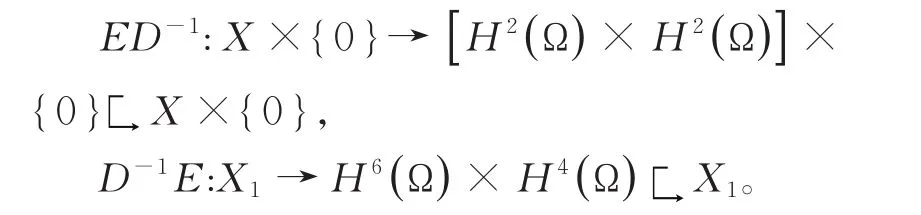
从而ED-1,D-1E都是线性紧算子。恒等算子与紧算子的和是Fredholm算子，所以由式(17)和 (18)，可推出BD-1,D-1B都是Fredholm算子，从而有

显然有

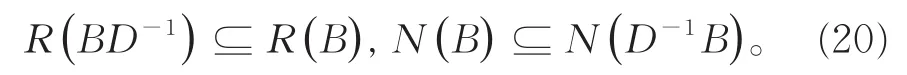
由式(19)和 (20)，得

因此，B:X1→X×{0}是Fredholm算子。又B的共轭B*=B，由Fredholm算子指标的性质，有

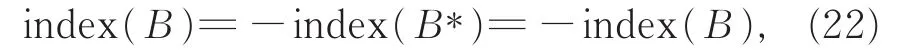
这意味着B:X1→X×{0}是零指标Fredholm算子。由此可得

其中W是X×{0}的一个闭子集，且满足

从而有

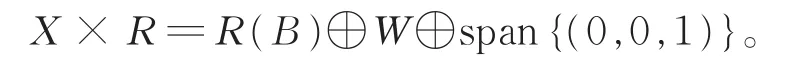
又B:X1→X0×R。所以有

其中，

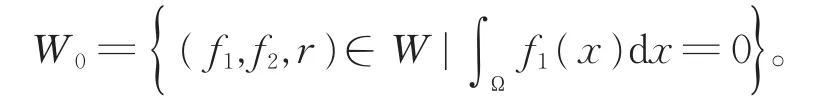
因此，

所以有

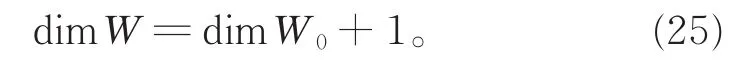
由式(23）～（25)，可推出R(B)在X0×R中的余维数满足:

这意味着B:X1→X0×R是零指标Fredholm算子。从而，由C的紧性以及式 (15)，推出FU(1/2,0,h2ρ1+3/2)是零指标的Fredholm算子。另外，由ρ1简单的假设条件以及引理1，可推出

从而

因此，引理2中条件(iii)被满足。

第2步证明

笔者称R(FU(1/2,0,h2ρ1+3/2))具有以下特征：

事实上，若

则存在(φ1,ψ1)∈X1，使得

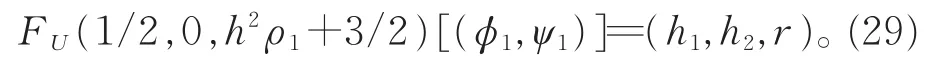
定义L:X1→X0：

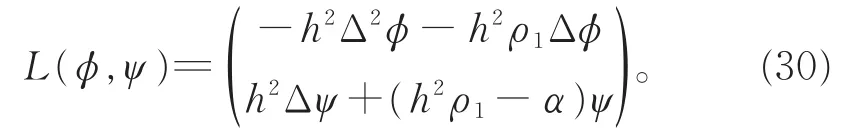
则L*=L。 由式(26)和(29)，有

从而有

由此可知，若

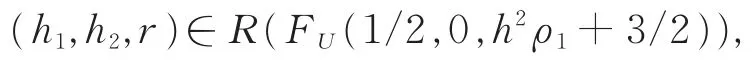
则有

这意味着

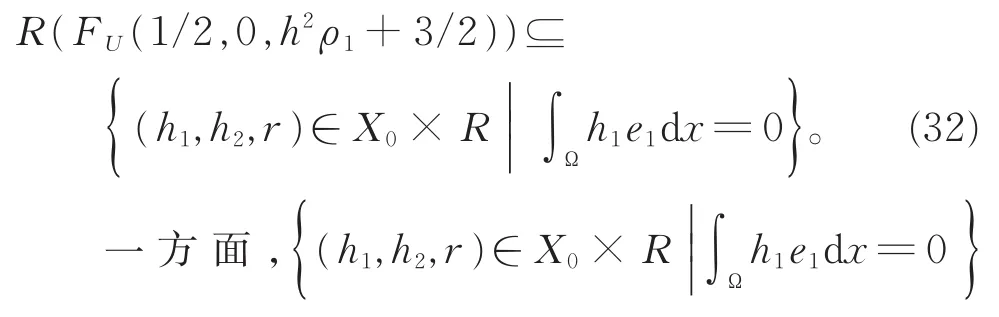
定义了X0×R中的一个余维为1的集合。另一方面，由FU(1/2,0,h2ρ1+3/2)是零指标的 Fredholm算子以及式(27)，有

因此，由式(32)和(33)，可推出式(28)成立。

易见

而由式(5)，有

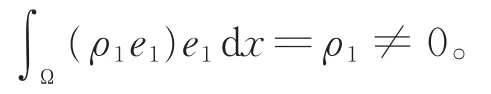
因此

即引理2中条件(ii)和(iv)被满足。

综上，引理2的所有条件均被满足。定理1的结论可由引理2推出。定理证毕。