弱拉回平坦序S-系对序幺半群的刻画

梁星亮，龙斌，徐盼盼

（陕西科技大学文理学院，陕西西安710021）

半群及其S-系形成了半群的S-系理论，该理论已广泛应用于代数自动机理论、数学语言学、密码学等数学学科[1-2]。S-系理论的中心问题之一是研究半群S的同调分类。为了研究序幺半群的融合问题，FAKHRUDDIN[3]引入了S-系的序代数理论——序S-系理论(其中S是序幺半群)。SHI等[4]利用序同余给出了张量积的新定义，并给出了序同余类以及序关系的具体刻画。随后，基于文献[5-9]，序S-系逐渐发展成为比较成熟的理论体系，并得到了广泛应用。

强平坦性质是S-系范畴中重要的同调性质之一，SHI[5]于2005年将该性质推广至序S-系范畴，给出序幺半群S的理想是强平坦的等价刻画。ERSHAD等[6]进一步研究了强平坦覆盖，给出每一个序S-系有强平坦覆盖的序幺半群的代数结构。受S-系范畴中同调理论的启发，赵梅梅[7]在序S-系范畴中推广了强平坦性质，引入了弱拉回平坦性，并利用Rees商序S-系的这一性质研究了序幺半群的同调分类问题。本文将进一步研究弱拉回平坦序S-系，首先，刻画序S-系的直积保持弱拉回平坦性质的序幺半群类，其次，讨论序S-系的弱拉回平坦性质与条件(P)、投射性一致的序幺半群的结构，最后，研究序S-系具有拉回平坦覆盖的条件。通过序S-系的弱拉回平坦性质,刻画了一些新的序幺半群的结构,推广了已有结果。本研究是对序S-系理论在序半群中应用的深化,对于揭示序S-系理论与S-系理论的区别与联系，探索平坦性质在序S-系中的应用具有重要意义。

方便起见，首先给出文中所要用到的一些基本概念。假设S是序幺半群，1是其单位元。

设A是一个带有偏序≤的非空集合。若存在映 射f:A×S→A，(a,s)↦as，满足对任意的a,a′∈A和s,t∈S，有

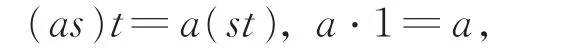
以及

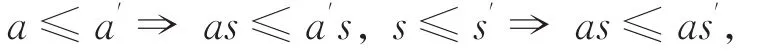
则称(A,f)为一个序右S-系，通常简记为AS。 类似地，可定义序左S-系SA。

设A,B是序右S-系，若对任意的a,a′∈A，s∈S，有

则称映射f:A→B为从A到B的序S-同态。所有序右S-系以及序右S-系之间的同态构成一个范畴，称之为序右S-系范畴。在序右S-系范畴中，一簇右S-系{Ai|i∈I}的直积和余直积分别为卡氏积和不交并，分别记为和

若AS满足条件：

则称序S-系AS是强平坦的。

若AS满足条件 (P)和条件 (E′)：

则称序S-系AS是弱拉回平坦的。因为每一个满足条件(E)的序S-系满足条件(E′)，所以，每一个强平坦序S-系是弱拉回平坦的。但由文献[8]中的定理1以及下面的推论1知，反之不然。

若对任意s,t∈P,存在p∈P,使得ps=pt(sp=tp),则称序幺半群S的一个序子幺半群P是左(右)collapsible 的[8]。显然，含有左(右)零元的序幺半群是左(右)collapsible的。若对任意s,t∈P,z∈S,当sz=tz时,存在p∈P使得ps=pt,则称序幺半群S的一个序子幺半群P是弱左collapsible的。显然，S的每一个左collapsible序子幺半群都是弱左collapsible的，反之不然。例如：正整数集N*关于数的乘法做成了一个序幺半群，其上的序关系为自然序。容易验证N*是弱左collapsible而非左collapsible。

1 基本性质

讨论关于弱拉回平坦序S-系的一些基本性质。首先，利用序S-系的强凸性质给出了弱拉回平坦序S-系关于余直积封闭。

命题1设其中Ai是AS的强凸序S-子系，i∈I，则AS是弱拉回平坦的当且仅当每一个Ai是弱拉回平坦的。

证明必要性。假设AS是弱拉回平坦序S-系。则AS满足条件(P)和条件(E′)。下证Ai满足条件 (P)和条件(E′)，i∈I。

设在Ai中 ，as≤a′s′，a,a′∈Ai,s,s′∈S，则as≤a′s′也在AS中成立。因为AS满足条件 (P)，所以存在a″∈A,u,v∈S使得a=a″u,a′=a″v,us≤vs′。由a∈Ai，必有a″∈Ai，否则存在某个j≠i，j∈I,使得a″∈Aj，从 而a=a″u∈Aj，矛盾。因此，Ai满足条件(P)。类似地可证Ai满足条件(E′),故Ai是弱拉回平坦的。

充分性。设每个Ai是弱拉回平坦的，i∈I。若as≤a′s′,a,a′∈Ai,s,s′∈S，则a,a′属于AS的同一个强凸序S-子系Ai,i∈I。否则，存在j∈I,i≠j，有a∈Ai,a′∈Aj，从而as∈Ai,a′s′∈Aj，由Aj的强凸性可知，as∈Aj，显然矛盾，故a,a′∈Ai。又因为Ai满足条件 (P)，所以存在a″∈Ai,u,v∈S，使得a=a″u,a′=a″v,us≤vs，而a″∈Ai⊆A，说 明AS满足条件(P)。类似可证AS满足条件(E′)。因此，AS是弱拉回平坦的。

下面的命题给出了弱拉回平坦性质保持有向上极限，关于序S-系有向上极限的定义和相关性质请参考文献[9]。

命题2弱拉回平坦序右S-系的正向系统有向上极限是弱拉回平坦的。

证明假设(Ai,φi,j)是关于有向集I的弱拉回平坦序右S-系的正向系统，(A,αi)是其有向上极限。下证A满足条件(P)和条件(E′)。

若a,a′∈A和s,s′∈S满足as≤a′s′，则存在i,j∈I,ai∈Ai,aj∈Aj使得a=αi(ai),a′=αj(aj)。因为I是有向集，所以存在k≥i,j，使得φi,k(ai)s≤φj,k(aj)s′在Ak中成立。又由于Ak满足条件 (P)，所以存在a″∈Ak，u,v∈S，使得φi,k(ai)=a″u,φj,k(aj)=a″v,us≤vs′。从而αkφi,k(ai)=αk(a″)u，αkφj,k(aj)=αk(a″)v，即a=αi(ai)=αkφi,k(ai)。类似地，a′=αk(a″)v。因此，A满足条件(P)。类似可证A满足条件(E′)。故A是弱拉回平坦的。

在序S-系范畴中，强平坦性质严格推出弱拉回平坦性质，下面的命题给出了在右collapsible序幺半群条件下，此2性质一致。

命题3设S是右collapsible序幺半群。则每一个弱拉回平坦的序S-系是强平坦的。

证明由定义容易证得，此略。

2 序幺半群的同调分类

主要利用序S-系的弱拉回平坦性质研究序幺半群的同调分类问题。首先刻画弱拉回平坦性质从直积转移到每个分量上的序幺半群的结构。

推论1一元序S-系={θ}是弱拉回平坦的当且仅当S是弱右reversible和弱左collapsible序幺半群。

证明由文献[7]中的推论1.1以及文献[8]中的定理1直接可得。

定理1设S是序幺半群，则以下条件等价：

(1)对任意的一簇序右S-系若是弱拉回平坦的，则每一个Ai是弱拉回平坦的，i∈I；

(2)一元序S-系是弱拉回平坦的；

(3)S是弱右reversible和弱左collapsible序幺半群。

证 明(1)⇒(2)。 因为如果AS是弱拉回平坦的，那么ΘS也是弱拉回平坦的。

(2)⇒(3)。由推论1可得。

(3)⇒(1)。假设对任意的一簇序右S-系是弱拉回平坦的。则AS满足条件 (P) 和条件(E′)。设ais≤a′it，ai，a′i∈Ai，s,t∈S，因为S是弱右reversible序幺半群，所以存在u1,v1∈S使得u1s≤v1t。考虑固定元素aj∈Aj,j≠i，令

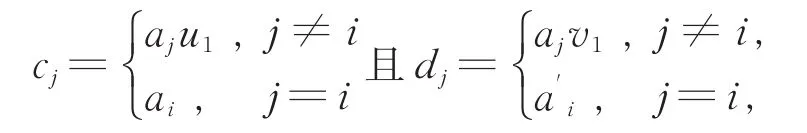
则(cj)Is≤(dj)It。又由于AS满足条件(P)，所以存在(a″j)I∈A，u,v∈S，使得 (cj)I=(a″)j Iu，(dj)I=(a″j)Iv，us≤vt。显然ai=a″iu,a′i=a″iv，因此Ai满足条件(P)。类似可证Ai满足条件(E′)。

自然地，下面考虑弱拉回平坦序S-系关于直积封闭的序幺半群的结构。

定理2对于任意的序幺半群S，以下叙述等价：

(1)对任意的一簇弱拉回平坦序S-系是弱拉回平坦的；

(2)对每一个非空集I，SI是弱拉回平坦的；

(3)对任意的a,b∈S，非空集L(a,b)={(u,v)∈S×S|ua≤vb}是一个循环序左S-系，且非空集l(a,b)={s∈S|sa≤sb}满足：若存在z∈S使得(a,b)∈ρz，则l(a,b)是S的一个主左理想。

证明(1)⇒(2)显然。

(2)⇒(3)。假设对每一个非空集I，SI是弱拉回平坦的，则SI满足条件(P)和条件(E′)。由文献[10]中的定理3.3，对任意的a,b∈S，非空集L(a,b)是一个循环序左S-系。现假设存在z∈S，使得(a,b)∈ρz，并且用集合I来标记l(a,b)，即其中的第i个分量是si。则≤且az=bz。由于SI满足条件(E′)，所以存在ˉ∈SI,u∈S使得ˉ=,ua≤ub。于是u∈l(a,b),si=ziu，其中zi是ˉ的第i个分量，说明l(a,b)是S的一个主左理想。

(3)⇒(1)。假设Ai(i∈I)是弱拉回平坦序S-系。由文献[10]中的定理 3.3 知满足条件(P)。下证满足条件 (E′)。

假设 (xi)Ia≤ (xi)Ib,az=bz，(xi)I∈a,b,z∈S。则对每一个i∈I，xia≤xib,az=bz。因 为 每 一 个Ai满足条件(E′)，所以存在zi∈Ai,ui∈S，使得xi=ziui,uia≤uib。显然l(a,b)≠∅，且(a,b)∈ρz。根据假设条件，对每一个i∈I，存在u∈l(a,b)，使得ui∈Su。因此，ua≤ub，且存在wi∈S，使得ui=wiu。从而有(xi)I=(ziui)Iu，故满足条件 (E′)。

接下来考虑利用循环序S-系的弱拉回平坦性质刻画序幺半群的结构。

引理1设ρ是序幺半群S上的序右同余，循环序右S-系S/ρ是弱拉回平坦的当且仅当S/ρ满足条件 (P)，且

证明充分性。根据弱拉回平坦的定义，只需证S/ρ满足条件 (E′)。假设 [x]s≤ [x]s′,sz=s′z,则 [xs] ≤ [xs′],xsz=xs′z。 由假设条件知，存在u∈S，使得uρ1,uxs≤uxs′。 从而 [x]=[1]x=[u]x=[1]ux,(ux)s≤ (ux)s′。 故S/ρ满足条件(E′)。

必要性 。假设s,s′,z∈S,[s]≤ [s′],sz=s′z。由条件(E′)知 , 存在x,u′∈S使得 [1]=[x]u′,u′s≤u′s′。令u=xu′，则uρ1,us≤us′。

引理2设ρ是序幺半群S上的序同余，若循环序S-系S/ρ是弱拉回平坦的，则R=[1]ρ是S的一个弱右reversible和弱左collapsible序子幺半群。

证明 因为弱拉回平坦序S-系满足条件(P)，所以由文献[6]中的引理1.3知，R=[1]ρ是S的弱右reversible 序子幺半群。现假设sz=s′z，s,s′∈R,z∈S，则有sρs′，由引理 7，存在u∈S使得uρ1,us≤us′。显然u∈R, 即R=[1]ρ是S的弱左collapsible序子幺半群。

根据弱拉回平坦序S-系的定义，每一个弱拉回平坦序S-系均满足条件(P)，反之不然。下面的定理给出了对于循环序S-系，条件(P)与弱拉回平坦性质一致的序幺半群的刻画。

定理3对任意的序幺半群S，以下条件等价：

(1)所有满足条件(P)的循环序S-系是弱拉回平坦的；

(2)S的每一个凸的弱右reversible序子幺半群P满足条件(C)：对任意的u,v∈P，若uz≤vz,z∈S，则存在w∈P，使得wu=wv。

证明(1)⇒(2)。假设P是S的一个凸的弱右reversible序子幺半群，且ρ=θ(P×P)。由文献[6]中的引理2.1，S/ρ满足条件(P)。根据假设条件，S/ρ是弱拉回平坦的，由引理8知，[1]ρ是S的弱左collapsible序子幺半群，从而[1]ρ满足条件(C)。

下证P满足条件(C)。设s,t∈P和z∈S满足sz≤tz。因为P⊆[1]ρ，所以存在r∈[1]ρ，使得rs=rt。 由于rρ1，所以存在u1,v1,w1∈P使 得u1≤v1r≤w1。由P的凸性可知，v1r∈P，从而有(v1r)s=(v1r)t。因此P满足条件(C)。

(2)⇒ (1)。设S/ρ满足条件 (P)，且P=[1]ρ。则P是一个弱右reversible序左单式子幺半群。故P是一个凸的弱右reversible序子幺半群。根据假设条件，P满足条件(C)。现假设[s]≤[t],sz=tz。因为S/ρ满足条件(P)，所以存在u,v∈P，使得us≤vt，从而u(sz)≤v(tz)。进一步，由于P满足条件 (C)，所以存在r∈P，使得ru=rv。因此，(ru)s≤(rv)t=(ru)t，故S/ρ是弱拉回平坦的。

下面的定理给出了循环序S-系投射性与弱拉回平坦性一致的序幺半群的刻画。

定理4设S是一个含有右零元的序幺半群，则以下条件等价：

(1)所有的弱拉回平坦循环序右S-系S/ρ是投射的；

(2)所有的强平坦循环序右S-系S/ρ是投射的；

(3)S的每一个凸的左collapsible序子幺半群含有一个左零元；

(4)S的每一个凸的弱右reversible和弱左collapsible序子幺半群含有一个左零元。

证明(1)⇔(2)。由命题3可得。

(2)⇔(3)。即文献[6]中的命题2.4。

(3)⇔(4)。因为S是一个含有右零元的序幺半群，所以S的每一个弱左collapsible序子幺半群都是左collapsible的。而每一个左collapsible序子幺半群又是弱右reversible的，因此，结论成立。

为了刻画循环序S-系具有弱拉回平坦覆盖的序幺半群的结构，需给出

引理3设P⊆S是弱右reversible序子幺半群，且ρ=θ(P×P)，则

(1)P⊆ [1]ρ；

(2)[s]≤[t]当且仅当存在u,v∈P使得us≤vt；

(3)S/ρ满足条件(P)；

(4)设S是一个含有右零元的序幺半群。若P是S的一个弱左collapsible序子幺半群，则S/ρ是弱拉回平坦的。

证明(1) ～(3)即为文献[6]中的引理2.1。

由命题3以及文献[6]中的引理2.2即可得(4)。

定理5设S是一个含有右零元的序幺半群，则以下条件等价：

(1)循环序右S-系S/ρ具有弱拉回平坦覆盖；

(2)循环序右S-系S/ρ具有强平坦覆盖；

(3)[1]ρ包含一个左collapsible序子幺半群R，使得对任意的u∈[1]ρ，uS∩R≠；

(4)[1]ρ包含一个弱右reversible和弱左collapsible序子幺半群R，使得对任意的u∈[1]ρ,uS∩R≠。

证明(1)⇒(2)。由命题3可得。

(2)⇔(3)。即文献[6]中的命题3.4。

(3)⇒(4)。因为S是一个含有右零元的序幺半群，所以S的每一个弱左collapsible序子幺半群都是左collapsible的。而每一个左collapsible序子幺半群又是弱右reversible的，因此，结论成立。

(4)⇒(1)。由引理3以及文献[6]中的引理3.1和推理3.3可得。

推论2设S是一个含有右零元的序幺半群，则一元序S-系ΘS具有弱拉回平坦覆盖当且仅当存在一个弱右reversible和弱左collapsible序子幺半群R⊆S，使得对任意的u∈S，存在s∈S，满足us∈R。

最后给出一元序S-系具有条件(P)覆盖与强平坦覆盖的序幺半群的等价刻画。

推论3一元序S-系ΘS具有条件(P)覆盖当且仅当存在一个弱右reversible序子幺半群R⊆S，使得对任意的u∈S，存在s∈S，满足us∈R。

证明由文献[6]中的命题3.4可得。

推论4一元序S-系ΘS具有强平坦覆盖当且仅当存在一个左collapsible序子幺半群R⊆S，使得对任意的u∈S，存在s∈S，满足us∈R。

证明由文献[6]中的命题3.5可得。

3 小 结

在S-系范畴中利用弱拉回平坦性质刻画了序幺半群的结构。主要研究了弱拉回平坦性质关于直积封闭的序幺半群类，刻画了弱拉回平坦性质与条件(P)、投射性一致的序幺半群的结构，给出了循环序S-系具有弱拉回平坦覆盖以及一元序S-系具有条件(P)覆盖和强平坦覆盖的序幺半群的结构。特别地，在本文主要结论中，若将序S-系的偏序和序幺半群的偏序取为平凡序，就可以得到S-系理论的诸多经典结果，如本文中定理3的平凡序形式即为文献[11]中的定理10。