随机时滞微分方程的随机线性θ方法的均方指数稳定性
赵 梅 兰光强
(北京化工大学 理学院, 北京 100029)
引 言
随机时滞微分方程可用于刻画有重要应用并与时间相关,且依赖于过去状态的过程。近年来,关于这类方程数值解稳定性的研究取得了很大进展。Higham[1]研究了线性随机微分方程对应的随机θ方法的渐近稳定性; Zong等[2]研究了非线性方程对应的随机θ方法的均方指数稳定性;Wu 等[3]得到了中立型随机时滞微分方程相应数值解的指数稳定性;Lan等[4]得到了带马氏切换的中立型随机时滞微分方程的数值解指数稳定的充分条件。当扩散系数不满足线性增长条件时, Huang[5]通过研究随机线性θ方法平凡解的渐近稳定性,证明了特定条件下随机线性θ(1/2≤θ≤1)方法的均方渐近稳定性,但是并没有给出收敛速度。
本文研究当扩散系数高度非线性时随机线性θ方法的均方指数稳定性,在给出随机时滞微分方程的随机线性θ方法和两种稳定性定义的基础上,证明了给定条件下随机线性θ方法的均方指数稳定性(从而几乎处处指数稳定),完善了文献[5]中的结论。
1 基本假设和定义
对于一个抽象的全集Ω,F是Ω的子集类,P表示概率测度,令(Ω,F,{Ft}t≥0,P)是一个完全概率空间,σ代数流{Ft}t≥0满足基本条件(即单增、右连续且F0包含所有零测集)。定义期望E为Ω上随机变量关于P的积分。W(t)是定义在概率空间上的标准布朗运动。
考虑以下形式的随机时滞微分方程

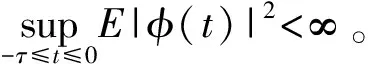
考虑随机线性θ方法(SLT方法),即划分格子点0=t0 (1) 注意到当θ>0时式(1)是隐式方法,为使式(1)有定义,通常需要使系数f满足特定条件(如单边Lipschitz条件)。 定理1假定式(1)有定义,若系数f、g满足 2〈u,f(t,u,v)〉+|g(t,u,v)|2≤-C1|u|2+C2|v|2,C1>C2>0 (2) 证明:定理1的证明分5步进行。 ① 方程(1)可变换为 (3) ② 证明存在0 (4) 事实上,有 (5) 又由式(2)可得 移项后,式(4)得证。 ③ 将式(4)代入式(3),有 |Fn+1|2≤(1-CΔ)|Fn|2+C2Δδ|yn-m+1|2+C2Δ(1-δ)|yn-m|2+Mn 又由于对任意的A>1,都有 A(n+1)Δ|Fn+1|2-AnΔ|Fn|2≤A(n+1)Δ[(1-CΔ)|Fn|2+C2Δδ|yn-m+1|2+C2Δ(1-δ)|yn-m|2+Mn]-AnΔ|Fn|2≤A(n+1)Δ(1-CΔ-A-Δ)|Fn|2+A(n+1)ΔC2Δδ|yn-m+1|2+A(n+1)ΔC2Δ(1-δ)|yn-m|2+A(n+1)ΔMn≤R1A(n+1)Δ|Fn|2+R2A(n+1)Δ|yn-m+1|2Δ+R3A(n+1)Δ|yn-m|2Δ+A(n+1)ΔMn (6) 式(6)中,R1=1-CΔ-A-Δ,R2=C2δ,R3=C2(1-δ),R2+R3=C2。 对式(6)从n=0到n=k-1求和,得 (7) 注意到R1|Δ=0=0,且 R′1(Δ)=-C+A-ΔlnA (8) 当1 (9) 所以有 (10) 将式(10)代入式(7),有 整理得 (11) 式(11)中 (12) (13) 将式(12)、(13)代入式(11),有 合并系数得 (14) 式(14)中 (15) ④ 证明AkΔE|Fk|2有界。 考虑式(15)中k1+k2Aτ+Δ+k3Aτ+Δ的正负。 首先考虑R1(C1θ-Aτ+ΔC2θδ)的正负。 由0 eC-C2Aτ+Δ>A (16) 在式(16)的条件下,有C-C2Aτ+Δ≥lnA,进而C-C2Aτ+Δ≥A-ΔlnA。 (17) 对式(17)两边取期望得 由此得到了AkΔE|Fk|2的有界性。 整理式(9)得 故有 (18) 对式(18)两边乘AkΔ并取期望,得 记 则有AkΔE|yk|2≤b+q1A(k-m+1)ΔE|yk-m+1|2+q2A(k-m)ΔE|yk-m|2。 令ak=AkΔE|yk|2,有递推式ak≤b+q1ak-m+1+q2ak-m,从而得到 (19) 式(19)中显然式(19)最后一个不等式中a的下标均小于等于0。 即 第⑤步证明完成。至此,得到了随机线性θ方法数值解的均方指数稳定性,定理1得证。证毕。 本文参考文献[4]中θ-EM数值格式的方法,研究了随机时滞微分方程随机线性θ方法的均方指数稳定性。与文献[5]相比,本文处理了更为复杂的滞后项,并在相同条件下得到了随机线性θ方法的均方指数稳定性(1/2<θ≤1),从而几乎处处指数稳定,比文献[5]中的结论更完善。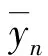



2 主要结果和证明


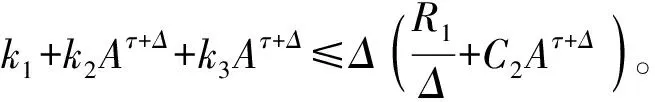


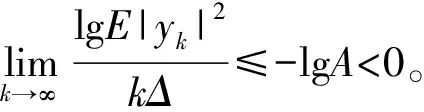
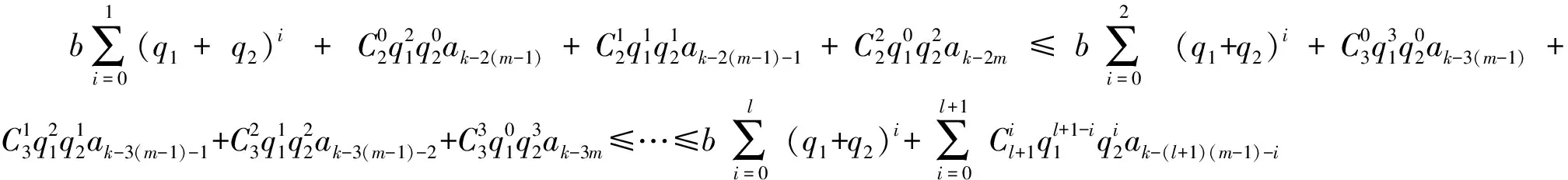
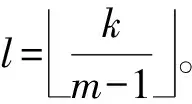

3 结束语

