基于自适应动态时间规整(DTW)的GA- FCM多阶段间歇过程故障诊断

梁秀霞 陈娇娇 严 婷 周 颖 张 燕

(河北工业大学 人工智能与数据科学学院， 天津 300130)

引 言

间歇生产是重要的工业生产过程，由于具有体积小、价值高的优点，广泛应用于发酵工程、半导体制造等批量生产中[1-3]。近年来，间歇过程在工业化、集成化生产中所占的比例逐年升高，因此其安全性与可靠性也备受关注。

间歇过程的生产特点使得生产过程中会出现数据不等长问题，Nomikos等[4]为解决该问题提出最短长度法，即将所有批次数据长度统一为众多批次中数据长度最短的那批数据的长度，该方法虽然简单，但是会造成数据的丢失，使数据之间的相关性降低；Cho等[5]实时计算待测生产过程中已知的测量数据与历史过程数据相对应的那一部分距离，选择距离最小的值所对应的批次，将该批次的过程数据用于数据填充，但是该方法计算量过于复杂且单纯地把距离作为选取标准也不能代表实际生产过程中的一些潜在关系和特点。

间歇过程还存在一个固有特性—多阶段特性，即随着生产过程的进行，控制目标和主导变量会随之发生改变[6-8]。目前，多向核主元分析(MKPCA)方法在间歇过程中的应用较为常见[9]，但传统的MKPCA方法一般会使用整个批处理数据来构建模型，而忽略掉生产过程中的局部特征。针对多阶段特性，梁小凡等[10]提出基于模糊C-均值算法的分时段过程监控算法实现间歇过程的阶段划分，但是模糊C均值算法对初始聚类中心比较敏感，初始聚类中心选取不当会使阶段划分不准确，进而影响过程监测的准确性。张成等[11]提出了一种模糊有序聚类算法，将模糊策略引入阶段划分中，但其只针对单独的批次数据进行聚类，最后才整合数据，准确度不高。

针对上述间歇过程研究方法的不足，本文提出自适应动态时间规整(DTW)算法以解决数据不等长问题，实现了N个批次数据时间长度一致的目标。针对间歇过程多阶段特性，采用遗传算法与模糊C-均值聚类(FCM)算法相结合的方法(GA- FCM)对间歇过程进行阶段划分，之后用MKPCA对每个子阶段分别建立模型并完成故障检测。

1 多向核主元分析故障诊断模型

间歇生产的过程数据可以表示为三维矩阵X(I×J×K)，I代表采样批次，J代表过程变量，K代表采样时刻。在建模时需要先将三维数据展开成二维数据，展开方式主要有批次展开和变量展开[12-14]，数据展开后MKPCA的建模过程与核主元分析(KPCA)相同。

KPCA的基本思想是首先通过非线性映射将输入空间映射到特征空间，然后提取该特征空间中的主要分量。设输入样本集Xh={x1,x2,…,xN}，其中xk∈Rm，N为样本数。通过非线性映射φ将输入数据从输入空间投影到KPCA空间，记为φ(xk)。定义核矩阵K=[Kβγ]，其中

Kβγ=k(xβ,xγ)=〈φ(xβ),φ(xγ)〉

(1)

引入核函数可以避免同时执行非线性映射和计算特征空间中两个向量内积的问题。对于任意测试向量x的主要分量t可按式(2)计算

(2)

式中，k=1,2，…,p，p为保留主元数，α为归一化后的核矩阵的特征向量。T2和SPE统计量及控制限可参考文献[15]来计算。

2 自适应DTW算法

针对间歇生产过程中数据的不等长问题，采用一种时间长度自适应DTW算法，使采集的批次时间长度保持一致。本文采用欧氏距离计算两轨迹A、B之间的点- 点距离，从而可以获得a×b组局部距离。若设a×b中第λ个局部距离为d(μ(λ),η(λ))，则

d(μ(λ),η(λ))={A[μ(λ),:]-B[η(λ),:]}W{A[μ(λ),:]-B[η(λ),:]}T

(3)

式中，μ(λ)、η(λ)表示样本的时标，W是权矩阵，W=E，E是单位矩阵，A[μ(λ),:]表示A中第μ(λ)个行向量；B[η(λ),:]表示B中第η(λ)个行向量。在进行DTW算法同步化时求取的是两轨迹之间的最短距离，在最短距离的基础上实现数据的处理。

用自适应DTW算法解决数据不等长问题时，计算采集的N批实验数据平均时间长度L，选取N批里时间长度最接近L的批次Nq作为参考轨迹。当LNlLNq(l≠q)时进行非对称式同步化，得到同步化后的N个批次数据；将N个批次数据进行平均化得到参考轨迹Rref，平均化方式如式(4)

(4)

得到参考轨迹后，将N批原始数据分别与Rref进行对称式DTW算法或非对称式DTW算法同步化，得到时间长度一致的N个批次数据。

将得到的N个批次的数据先按批次展开，然后进行标准化处理，将标准化后的数据再重新排列回X(I×J×K)的形式，然后再按变量展开，展开后沿时间轴方向将数据切割为K个时间片矩阵Tk(I×J)，计算每个时间片矩阵Ti与其他时间片矩阵Tj的相似度，并将相似度矩阵S(S∈RK×K)作为聚类算法的输入进行聚类分析。相似性度量的计算公式为

(5)

3 GA- FCM聚类算法的阶段划分

3.1 FCM算法

FCM算法是一种用0～1间的隶属度来确定每个样本点属于各个组的程度的模糊聚类方法[16]。隶属度在归一化条件下满足

(6)

FCM算法是一种最小化价值函数的迭代优化算法，价值函数定义为

(7)

式中，ugh∈(0,1)，cg为组g的聚类中心，w为模糊系数，dgh=‖cg-sh‖为第g个聚类中心与第h个数据点间的欧氏距离。使式(7)达到最小的必要条件为

(8)

(9)

FCM算法的缺点是对初始值较为敏感，初始值如果选取不合适会使聚类效果变差，因此本文使用遗传算法对初始聚类中心进行参数寻优，改善FCM的聚类效果。

3.2 GA- FCM算法

遗传算法是一种强大的随机算法，它通过选择目标函数将其与最优性概念联系起来，进而求得最优解。遗传算法是从代表问题可能解的一个种群开始的，并通过一些遗传操作(如选择、交叉和变异)有概率地修改种群，以寻求问题接近最优的解决方案。

3.2.1种群初始化

Smin是相似性矩阵S每一维的最小值向量，Smax是相似性矩阵S每一维的最大值向量。首先通过随机的方式在[Smin,Smax]区间内产生一代包含H个体的初始种群M1，该种群的计算方式为

M1=

(10)

式中，M1为第一代群体，是一个H行1列的向量组，每一行是一个1×2 400的向量，代表一个个体，由2 400个染色体构成，每个染色体是一个十进制编码的参数优化值，rand(0,1)则是0,1之间的随机数。

3.2.2选择

选择操作采用轮盘赌法，个体选择概率为

(11)

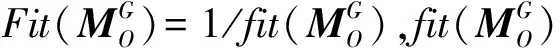
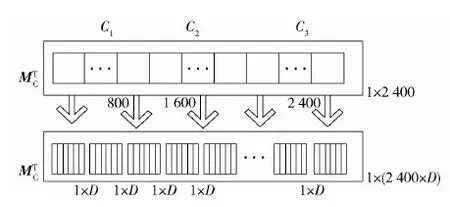
图1 编码过程Fig.1 Coding process

3.2.3适应度计算

首先对当代种群的个体进行解码，将二进制数转换为十进制，再将各个个体的聚类中心从一维矩阵转换为二维矩阵，如图2所示。

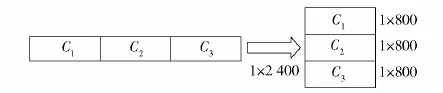
图2 矩阵的转换Fig.2 Matrix conversion

适应度计算公式为

(12)

式中，D1为类内距离，表示同一模式点集内各样本间的均方距离，计算式为

(13)

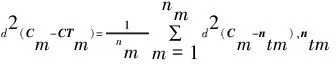
D2为类间距离，表示模式类之间的距离，计算式为

(14)

式中，Cr表示第r类样本集的聚类中心，Ce表示第e类样本集的聚类中心。

选取迭代过程中适应度最小的聚类中心作为遗传算法的解输出，将输出的聚类中心作为FCM算法的初始值代入式(7)～(9)，进行FCM的聚类过程，实现阶段划分。

改进FCM算法流程图如图3所示。

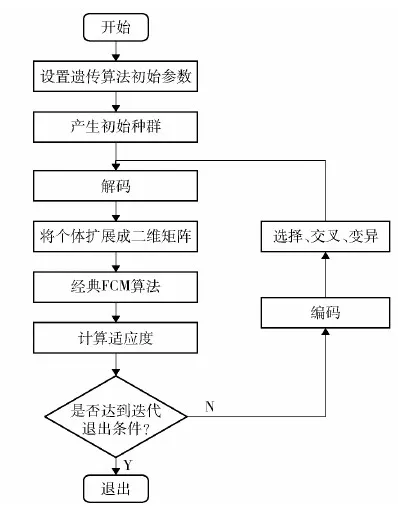
图3 改进FCM算法流程图Fig.3 Flow chart of GA- FCM algorithm

4 仿真结果

本文采用的间歇过程是青霉素生产的模拟补料分批发酵过程，此生产过程具有非线性和多阶段的特征。根据工艺菌体生长周期，青霉素发酵过程一般可以分为菌体生长、青霉素合成、菌体自溶3个阶段。PenSim2.0是青霉素生产的模拟软件，为检测青霉素的生产提供了标准平台，本文实验数据均通过此软件获得。

4.1 聚类有效性

聚类有效性可用类内距离与类间距离之比来衡量，即

(15)

D1数值越小，聚类效果越好；D2数值越大，聚类效果越佳。将两个指标结合起来，则F值越小代表聚类效果越好。

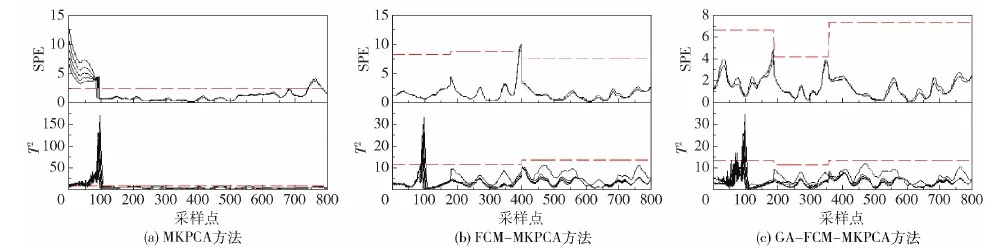
图5 正常批次仿真图Fig.5 Results of normal batch simulation

经式(15)计算可得，本文所提算法F值为1.6，FCM算法F值为2.3，可见本文所提算法聚类更为准确。

4.2 故障检测结果

本文选择了青霉素发酵过程中的17个变量进行研究，包括充气率、搅拌器功率、底物流加速率、底物流温度、底物浓度、溶解氧浓度、生物质浓度、青霉素浓度、培养体积、二氧化碳浓度、pH、生物反应器温度、产生的热量、酸流率、碱流率、冷水流量、热水流量，模拟了20个发酵时间从390 h到410 h不等、采样间隔为0.5 h的正常参考批次，其中这些批次的平均时间长度为400.2 h。选择发酵时间为400 h的这一批数据为Nq。最终采集的20个批次数据的时间长度经过自适应DTW算法后均调整到400 h，实现了数据的等长。

分别通过MKPCA算法、FCM- MKPCA算法和本文所提GA- FCM- MKPCA算法对间歇过程进行故障检测。

图4为本文所提算法的聚类结果。由图4可知，本文算法将间歇过程划分为3个阶段：1～188是第一阶段；189～357是第二阶段；358～800是第三阶段。此阶段划分满足青霉素实际生产过程的特点。阶段划分完成后，对3个阶段分别建立MKPCA模型，进行故障检测。

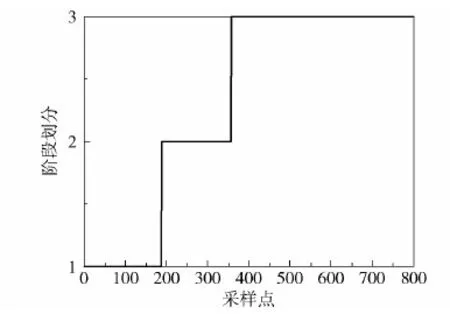
图4 GA- FCM算法阶段划分Fig.4 Stage division result of GA- FCM algorithm

MKPCA算法、FCM- MKPCA算法和本文所提GA- FCM- MKPCA算法对正常批次的检测结果如图5所示。

由图5可知，MKPCA算法T2误报率为12.35%，FCM- MKPCA算法T2误报率为1.95%，而本文所提方法将T2误报率降到了0.9%；MKPCA算法SPE误报率为17.15%，FCM- MKPCA算法SPE误报率为0.88%，本文所提算法SPE误报率为0.13%。可见利用本文所提方法划分阶段后再建立模型会降低误报率。

本文还采集了两种故障数据进行检测：故障1 对充气率引入故障信号，在200 h施加+3%阶跃信号，该信号持续至第300 h，诊断结果如图6所示；故障2在200 h时对充气率施加+0.2%斜坡信号，该信号持续至第300 h，诊断结果如图7所示。

图6 故障1检测图Fig.6 Diagnosis diagram of fault 1

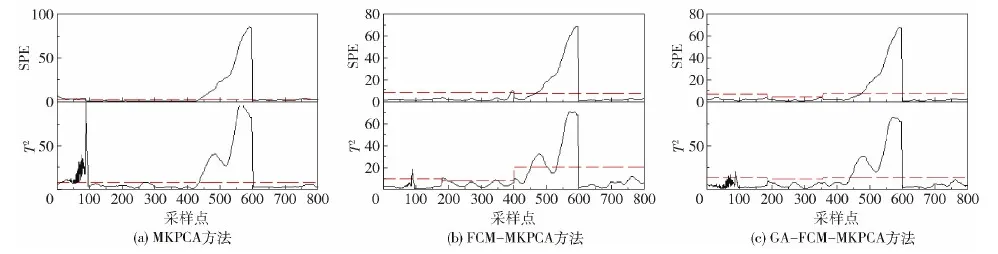
图7 故障2检测图Fig.7 Diagnosis diagram of fault 2

从图6可知，FCM- MKPCA算法T2漏报率为2.25%，MKPCA方法和本文所提方法漏报率为0，MKPCA算法T2误报率为10.38%，FCM- MKPCA算法T2误报率为3.63%，本文所提方法T2误报率为0.88%；3种方法的SPE漏报率均为0，而对于SPE误报率，MKPCA算法为16.75%，FCM- MKPCA算法为1%，本文所提算法降到了0.1%。由此可知，本文所提方法误报率大大降低，故障诊断精度明显提高。

从图7可知，对于T2漏报率，MKPCA算法为5.00%，FCM- MKPCA算法为10.13%，本文所提算法为5.25%，对于T2误报率，MKPCA算法为10.25%，FCM- MKPCA算法为3.5%，本文所提算法为0.75%；3种方法得出的SPE漏报率基本一致，而对于SPE误报率，MKPCA算法为16.63%，FCM- MKPCA算法为1.01%，本文所提算法为0。综上可知，本文所提方法的故障诊断准确度更高。

从图5～7可知，50～100采样点发生的误报比较多，这是因为在此阶段菌体进入发酵期，菌体浓度、溶解氧浓度、pH、碱补给等变量在此时段内发生波峰式明显变化，并没有趋于稳定值，虽然数据经过了MKPCA归一化处理，但仍然会有生物过程的波动特性，所以此时段误报最多。将青霉素发酵过程用本文方法分阶段后，把这一过程划分到第一阶段，并单独建立MKPCA的模型，据此获得此阶段下合理的T2、SPE的受控限，相比于整个批次获得的T2、SPE的受控限，利用第一阶段获得的受控限进行该阶段的故障检测，大大降低了误报率。

通过以上仿真实验的结果可知，无论是对阶跃故障还是对斜坡故障，本文所提方法的故障诊断精度都要比传统不分阶段的方法以及FCM分阶段的方法高。

5 结论

(1)针对间歇过程数据不等长问题，提出了一种自适应DTW算法。自适应DTW算法发挥了对称式DTW算法与非对称式DTW算法在算法上的互通性与互补性，将不等长数据变为等长数据，实现了多个批次数据轨迹的时间长度同步化。

(2)针对FCM算法在阶段划分中存在的对初始聚类中心敏感的问题，提出遗传算法与FCM算法相结合来完成聚类过程。遗传算法采用的是整体搜索策略，它从实际问题中抽离出来，采用全局搜索方式，通过选择、交叉、变异等操作完成搜索过程，具有强大的全局搜索能力。遗传算法可以有效、快速地解决FCM算法对初始聚类中心敏感且易于陷入局部收敛的问题。

(3)仿真实验的结果表明，GA- FCM算法比单一FCM算法有更高的聚类有效性，阶段划分更为准确，故障诊断精度也明显提高。