关于n-秩轮图2-adic Orlik- Solomon代数的研究

陈文娟 孙贵艳 王子璇 姜广峰

(北京化工大学 理学院， 北京 100029)

引 言

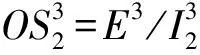
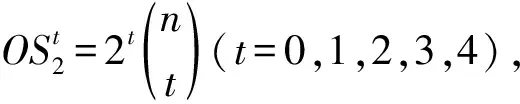
1 预备知识

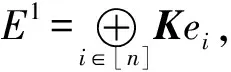
在外代数E上定义一个K-线性映射∂:Ep→Ep-1，且满足∂1=0,∂ei=1(i=1,…,n),∂(e1…ep)=

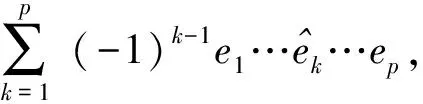
对于给定的超平面p元组S=(Hi1,…,Hip)=(i1,…,ip)，记eS=ei1…eip=ei1…ip,∩S=Hi1∩…∩Hip。若codim (∩S)=|S|，则称p元组S无关；若∩S≠Φ且codim (∩S)<|S|，则称p元组S相关；若p元组S=(H1,…,Hp)是极小相关的，则S={H1,…,Hp}为一个极小圈。

2 n-秩轮图的2-adic Orlik- Solomon代数

设Cn为一个有n个顶点的圈，第n+1个顶点与Cn的每个顶点相连成n条边，这样形成的图称为n-秩轮图。在n-秩轮图G中，G的边数(即超平面的个数)为2n，顶点个数为n+1，极小圈个数为n,其中极小圈的集合Cn={c1,c2,…,cn}，当n=4、5时，n-秩轮图如图1所示。

图1 4-秩轮图和5-秩轮图Fig.1 4-rank wheel graph and 5-rank wheel graph

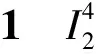
证明：不妨设p=i,则有epq∂eijk=±eijkq。在D4,1中，p有n种取法，q有2n-3种取法，而该n(2n-3)个向量在E4中基的序列各不相同，故有dim (D4,1)=n(2n-3)。引理1得证。

记

D′4,2={epq∂eijk|eijk∈Cn,p,q∈[2n]{i,j,k},p,q在同一个极小圈中}

D″4,2={epq∂eijk|eijk∈Cn,p,q∈[2n]{i,j,k},p,q不在同一个极小圈中}

D4,2={epq∂eijk|eijk∈Cn,p,q∈[2n]{i,j,k}}

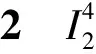
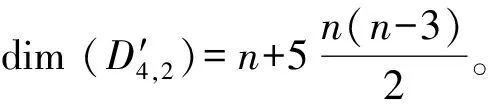
证明：首先，在D′4,2中，若p,q取自邻圈，对于n-秩轮图，任何一个极小圈都有2个邻圈，则p,q有2n种取法。将n个圈c1,c2,…,cn两两分为n组，有G1={c1,c2},G2={c2,c3},…,Gn={cn,c1},其中第i组Gi={ci,ci+1}如图2所示。

图2 第i组Gi的图示Fig.2 Graph of the group Gi

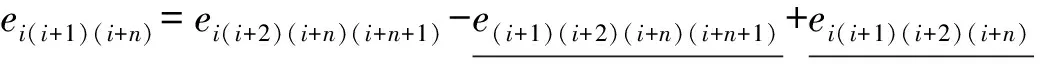
(1)

图3 n-秩轮图中的一个极小圈和一个非邻圈Fig.3 A circuit and its non-adjacent circuit in a n-rank wheel graph

式(1)中划线的分量可由D4,1中的元素线性表示，剩余的分量最多相差一个负号，故D′4,2中的向量在D4,1中是线性相关的，线性无关的向量个数为n。

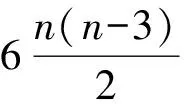
考虑5-秩轮图，如图4所示。

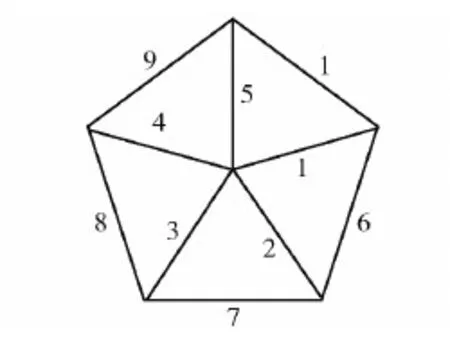
图4 5-秩轮图Fig.4 5-rank wheel graph

不妨取{i,j,k}∈{(1,2,6),(3,4,8)},p,q∈{(1,2,6),(3,4,8)}，则有

(2)

式(2)对应的6×216矩阵描述如下。

第1行的第1列元素为1，第30列元素为-1，第86列元素为1，其余列元素全为0；

第2行的第5列元素为1，第41列元素为1，第97列元素为-1，其余列元素全为0；

第3行的第11列元素为1，第56列元素为1，第112列元素为-1，其余列元素全为0；

第4行的第1列元素为1，第5列元素为-1，第11列元素为1，其余列元素全为0；

第5行的第30列元素为1，第41列元素为1，第56列元素为-1，其余列元素全为0；

第6行的第86列元素为1，第97列元素为1，第112列元素为-1，其余列元素全为0。

经计算，该矩阵的秩为5,且e26∂e348=e34∂e126-e38∂e126+e48∂e126-e12∂e348+e16∂e348，故该矩阵对应的6个向量是线性相关的，极大无关组个数为5。则对任意{i,j,k},{p,q,r}∈Cn,p,q∈{(i,j,k),(p,q,r)},有

(3)

式(3)所表示的向量组的秩为5，且有

ejk∂epqr=epq∂eijk-epr∂eijk+eqr∂eijk-eij∂epqr+eik∂epqr

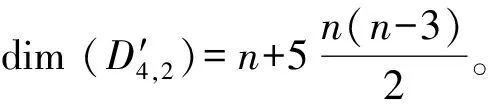
引理2得证。

①若p,q取自邻圈边，且epq∂eijk=ejkpq-eikpq+eijpq的各个分量是唯一出现的,则整个向量是线性无关的；

②若p,q取自非邻圈边，且epq∂eijk=ejkpq-eikpq+eijpq的3个分量中包含一个唯一的破圈，即整个向量都是唯一出现的，则整个向量是线性无关的；

③若p取自邻圈边，q取自非邻圈边，且epq∂eijk=ejkpq-eikpq+eijpq,则总有一个分量是唯一出现的，故整个向量是线性无关的，即dim (D″4,2)=n(2n2-10n+13)。

引理3得证。

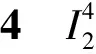
证明：在D4,2中，将p,q细分为p,q在同一个极小圈中和p,q不在同一个极小圈中两种情况，则有

D4,2=span(D′4,2)∪span(D″4,2)

设α=span(D′4,2)∩span(D″4,2)，则有

即

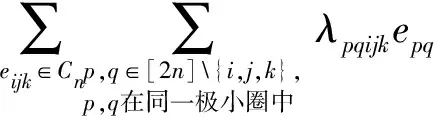
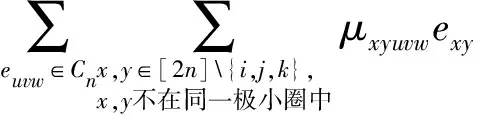
由于在D′4,2中，ejkpq、eikpq、eijpq不会在D″4,2中出现，故λpqijk=0,α=0，从而有

引理4得证。

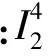
①p,q∈{i,j,k}时，epq∂eijk=0；

②p∈{i,j,k}、q∈[2n]{i,j,k}时，结果见引理1；

③p,q∈[2n]{i,j,k}时，结果见引理2和引理3。

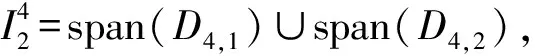
引理5得证。

定理1对于n-秩轮图，有

定理1得证。

推论1对于n-秩轮图，有

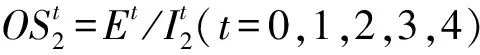
推论1得证。

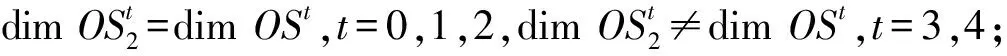
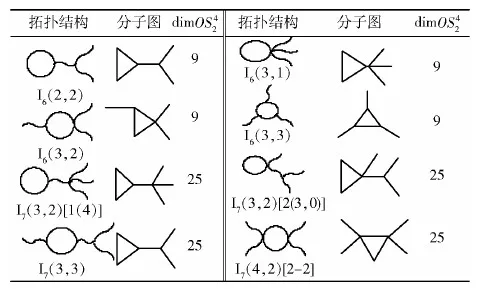
3 一类聚合物拓扑图的第4个2-adic Orlik- Solomon代数

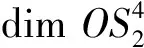
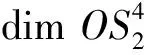
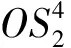
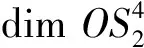
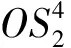
4 结束语