常微分方程教学与MATLAB 的有效结合
布仁满都拉
(赤峰学院数学与计算机科学学院,赤峰024000)
0 引言
在物理、化学、金融和医学等很多领域中经常建立数学模型研究相关问题,其中常微分方程是经常遇到的微分方程。因此,常微分方程是理科、工科和文科的很多专业的必修课。结合常微分方程和MATLAB 解算的教学方法比传统的理论讲授教法,更能提高学生的学习兴趣和知识的混合应用能力,下面用实例介绍常微分方程和MATLAB 的结合用法。
1 常微分方程的解析解和MATLAB解算
1.1 常微分方程的解析解
求方程y''-6y'+9y=4e3x通解。
解:我们先理论上算出方程组的解析解,然后给出它的MATLAB 解算。先求齐次方程的通解,特征方程为:

特征根为:
λ1,2=3
因此,齐次方程的通解为:
y=C1e3x+C2xe3x
由于3 是二重特征根,非齐次方程有形如:
y*=Ax2e3x
的特解。将它代入非齐次方程,比较x 的同次幂系数,得A=2,所以:
y*=2x2e3x
所求通解为:
y=2x2e3x+C1e3x+C2xe3x
1.2 MATLAB解算
下面用MATLAB 符号法求微分方程的解。
键入:
y=dsolve('D2y-6*Dy+9*y=4*exp(3*x)','x')
回车得出:
y=2*x^2*exp(3*x)+C5*exp(3*x)+C6*x*exp(3*x)
2 常微分方程组的解析解和MATLAB解算
2.1 常微分方程组的解析解
求解方程组

解:我们先理论上算出方程组的解析解,然后给出它的MATLAB 解算。
系数矩阵为:

特征方程为:
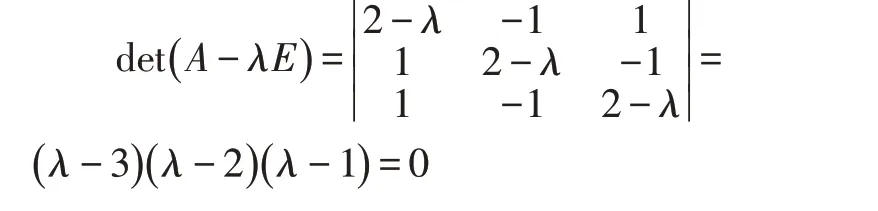
特征根为:λ1=3,λ1=2,λ1=1。
先求λ1=3 对应的特征向量:
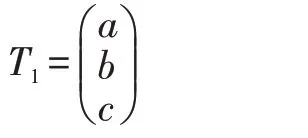
a,b,c 满足方程组:
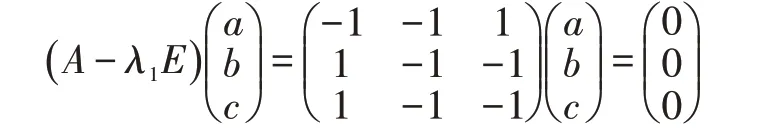
即:
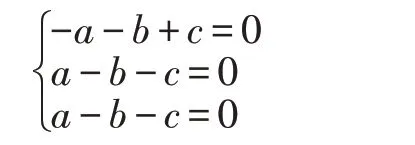
可得a=c,b=0,取一组非零解,例如令c=1,就有a=1,即:
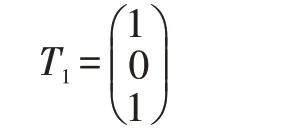
下面求λ2=2 对应的特征向量:

a,b,c 满足方程组:

即:
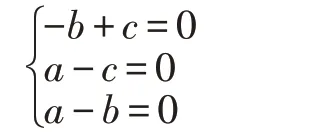
可得a=c,b=c,取一组非零解,例如令c=1,就有a=1,b=1,即:
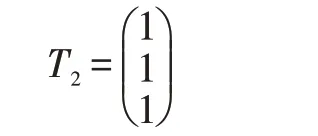
最后求λ3=1对应的特征向量:

a,b,c 满足方程组:

即:

可得a=0,b=c,取一组非零解,例如令c=1,就有b=1,即:

故方程组的通解是:

2.2 MATLAB解算
下面用MATLAB 符号求上述方程组的解析解:
键入:

回车得出:
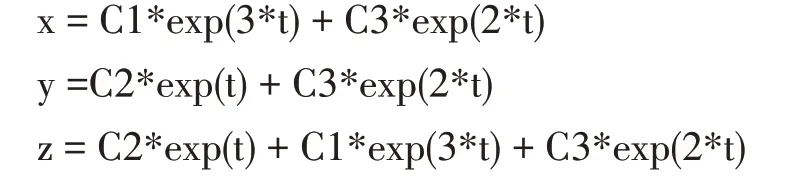
3 常微分方程初值问题数值解及MATLAB解算
3.1 常微分方程初值问题数值解
在很多问题中遇到的常微分方程的解析解是很难算出来的,这时,我们可以用数值方法求近似解。
求解2y'+4xy=1,y(0)=0。
解:先用分离变量法和常数变易试算齐次方程的通解:
2y'+4xy=0
分离变量,得:
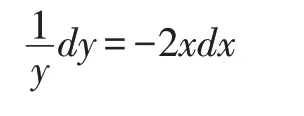
两端积分,得:
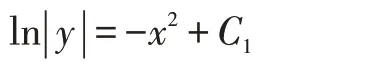
解出y,得:
y=Ce-x2
由常数变易法,令:
y=C(x)e-x2
为非齐次方程的解,代入后得:
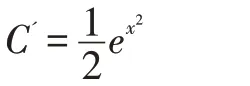
由于ex2的原函数不是初等函数,积分:
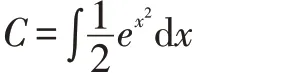
的计算无法进行。
3.2 MATLAB解算
下面用MATLAB 求该微分方程的数值解。
先建立如下M-函数文件
function y1=CDE(x,y)
y1=0.5-2*x*y;
在指令窗口中键入:
[x,y]=ode23(@CDE,[0 3],[0])
回车得出:


键入:

回车得出:
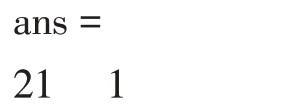
因此,在区间[0,3]上把x 分成了21 节点,对应地得出y 的21 个取值,即得到了微分方程的数值解。
进一步,键入:
plot(x,y)
回车画出数值解的图形,见图1。

图1 数值解的图形

