钢板外包混凝土组合剪力墙非线性屈曲分析

齐 益，顾 强，王华飞

（1.苏州科技大学 土木工程学院，江苏 苏州215011；2.河海大学 土木与交通学院，江苏 南京 210098）

钢板外包钢筋混凝土组合剪力墙（composite steel plate shear wall, C-SPW），即在内嵌钢板单面或双面浇筑一定厚度的混凝土板，使现浇钢筋混凝土墙板与内嵌钢墙板通过抗剪连接件和粘结作用形成整体、协同工作[1]。作为一种有效的新型的抗侧力构件，钢板外包混凝土组合剪力墙很好地结合了薄钢板剪力墙和钢筋混凝土剪力墙的优点，侧向刚度大、延性好、耗能能力强。

C-SPW 结构设计中墙板受剪承载力、混凝土板厚和栓钉间距的计算都涉及到组合板的屈曲问题。美国AISC 341-10 规范[1]规定C-SPW 的外包混凝土板应保证在墙体达到名义剪切强度前，内嵌钢墙板不发生屈曲。通过弹性屈曲分析得到的C-SPW 临界剪切荷载应大于其受剪屈服承载力。针对AISC 341-10 要求的CSPW 弹性屈曲分析，Astaneh-Asl[2]设想按弯曲刚度等效将混凝土板转换成纵、横钢肋，采用加劲板或正交异性板弹性屈曲理论计算C-SPW 的整体屈曲。AISC 于1997[3]提出应限制栓钉间距使得栓钉间钢板的局部剪切屈曲应晚于其剪切屈服。对于该受剪方形钢板，Astaneh-Asl[2]提出按钢梁加劲腹板的剪切屈曲计算，Dey 等[4]认为按方形板四边固接考虑，郭彦林等[5]对于防屈曲钢板剪力墙（BR-SPW）提出按方形板四边简支计算。

Smith 等[6]利用瑞利-里滋法分析了纯剪切作用下方形单侧约束组合板（1 层普通板和1 层约束板的组合板）的弹性屈曲问题，适用于钢板单面布置混凝土板组合剪力墙、组合梁等。Arabzade 等[7]提出了解决钢板单面外包高强度混凝土组合剪力墙弹性屈曲的理论计算模型，考虑了钢板与混凝土板的接触及栓钉的应变能，基于能量法得到了在剪切荷载作用下不同板高宽比、混凝土板厚度对应的组合板弹性屈曲系数。Lopatin 等[8]利用伽辽金法求解了四边固接、单向均匀受压下方形夹层板（三明治板）的弹性屈曲荷载。聂建国等[9-10]采用有限元方法对纯剪切作用下四边简支钢-混凝土组合板（1 层钢板、1 层混凝土板）进行了弹性屈曲分析，研究了组合板的局部屈曲特征，还采用夹层板理论研究了纯剪切作用下四边简支组合板的整体屈曲问题，求解了组合板的弹性屈曲荷载。郭彦林等[5]采用屈曲理论和有限元分析得到了BR-SPW 混凝土板最小厚度的计算公式。马欣伯[11]利用有限元分析得到了两边连接、另两边自由或设置加劲肋组合板（中间钢板、两面混凝土板）的弹性屈曲系数计算公式，理论分析了组合板的弹性整体屈曲荷载。Zhang 等[12]通过非线性有限元分析了均布压力作用下钢板內填混凝土组合（SC）剪力墙的局部屈曲问题，为保证钢板在局部屈曲前发生屈服，给出了栓钉间距与钢板厚度之比的限值。

目前，C-SPW 还未形成完整的设计方法，针对混凝土板厚度需求提出对组合板进行弹性屈曲分析的建议是否合理还有待验证；使用弹性理论分析组合板的屈曲问题，求解过程复杂；有限元弹性屈曲分析不能给出组合板屈曲强度的解析式，且由于弹性理论的理想化假设，得到的混凝土板厚度需求偏小。本文通过非线性有限元计算研究了钢板组合剪力墙在侧向荷载作用下的响应，提出了组合剪力墙钢板屈曲时对应层间侧移角的判别方法，分析了钢板厚度、混凝土板厚度、混凝土弹性模量及墙板高宽比对钢板屈曲的影响。

1 有限元模型

采用ABAQUS 建立了新颖的C-SPW 有限元模型，用于分析C-SPW 在侧向荷载下的非线性响应。模型考虑了钢板与混凝土板之间的粘结作用、钢框架对混凝土板边缘的挤压及焊接栓钉与混凝土板、钢板之间的相互作用。用本文有限元模型模拟了现有的C-SPW 试验，通过对比有限元计算结果与试验结果验证了本文有限元模型的精度。

1.1 边界条件

有限元分析旨在研究C-SPW 在水平荷载作用下的响应，研究不考虑边框架参与抵抗侧向荷载，钢框架仅提供C-SPW 的边界约束，且梁、柱节点为铰接，令钢框架始终保持弹性。如图1 所示，钢框架（用粗实线表示）简支于基础，平行于框架顶梁中轴线的单调水平荷载施加于梁、柱节点。内嵌钢墙板与框架刚接，承受平面内剪力。以钢墙板中心为坐标原点O，墙板厚度方向为Z 轴，板宽度、高度方向为X、Y 轴，建立有限元模型。约束边框架梁、柱单元平面外自由度UZ、URX、URY，并约束左柱脚的UX、UY 和右柱脚的UY，施加位移荷载的方向为X 轴正方向。

1.2 材性

钢材的弹性模量Es=206 GPa，泊松比为0.3，强化准则为各向同性强化。内嵌钢墙板和钢筋材料采用理想弹塑性模型模拟，屈服强度分别为235 MPa 和300 MPa。焊接栓钉的本构模型为双折线强化模型，强化段切线模量Et=0.02Es，屈服强度和抗拉强度分别为240 MPa 和400 MPa。边缘框架在有限元计算中要求不进入塑性，因此只定义其弹性模量Es=206 GPa。混凝土采用损伤塑性模型（CDP 模型）模拟，混凝土本构关系曲线、弹性模量、拉伸强度和压缩强度按我国《混凝土结构设计规范》[13]取值。

1.3 单元类型及相互作用

C-SPW 有限元模型如图2 所示，内嵌钢板为4 节点四边形线性缩减积分壳单元S4R，外包混凝土板为8节点六面体线性缩减积分实体单元C3D8R，栓钉为2 节点线性梁单元B31，钢筋为桁架单元T3D2。为模拟边框架梁柱翼缘板对混凝土板边缘的挤压作用，将梁单元（B31）与壳单元（S4R）耦合在一起模拟边框架，其中梁单元模拟框架对内嵌钢墙板的作用，壳单元模拟梁、柱翼缘板对混凝土板边缘的作用。

图1 FEM 边界条件

图2 FEM 单元类型

边框架的壳单元与梁单元为绑定约束，耦合了二者单元节点的所有自由度。由于本文不考虑边框架参与抗剪仅提供C-SPW 边界约束，且框架壳单元与梁单元中轴线对齐，二者耦合后对框架梁、柱截面的惯性矩影响很小，故此模拟方式可用于C-SPW 非线性有限元分析。构件间的焊接与埋入采用耦合重叠单元节点自由度模拟。混凝土板侧面与边缘框架的壳单元之间为接触作用，接触面法向为“硬”接触，允许接触面自由分离但禁止接触面相互穿透，忽略接触面切向摩擦作用。钢板与混凝土板之间采用非线性弹簧单元进行连接，切向弹簧单元力-位移关系按照混凝土与钢之间的粘结应力-滑移本构关系定义，法向弹簧单元本构关系与“硬”接触关系类似，即当钢板与混凝土板的单元节点分离时弹簧力为0，当二者接触或有穿透趋势时弹簧力线性增大，防止单元节点互相穿透。

1.4 有限元模型验证

国内外鲜有对钢板外包混凝土组合剪力墙（C-SPW）的试验研究，Aarbzadeh 等[14]试验研究了C-SPW 的抗侧力性能，试件CS 为钢墙板单侧现浇混凝土板，墙板高度与跨度均为530 mm，内嵌钢板及混凝土板厚分别为2 mm 和30 mm；框架梁、柱节点刚接，混凝土板与框架间设缝隙11.25 mm，往复加载。采用本文模型对该试件进行数值模拟，比较有限元模拟结果与试验结果的差异，验证本文有限元模型的合理性。有限元模型考虑了试件混凝土板与钢框架的间隙及框架节点条件，其几何尺寸及材料特性与试验试件相同，但加载方式不同，本文对有限元模型只进行单调加载，比较有限元计算曲线与试验骨架曲线。

CS 试件的滞回曲线如图3 所示，试件承载力最大值为542 kN，侧移极限为28 mm，滞回曲线比较饱满。CS 的试验骨架曲线与本文模型模拟曲线比较如图4 所示，可以看出，二者吻合较好，初始刚度十分接近；曲线的最大值分别为550 kN 与542 kN，相差1.5%；侧移极限相同；二者间细微的差别主要是由于加载制度的不同和试验装置不可避免的机械变形。由此可知，本文提出的有限元模型可以用于C-SPW 的有限元模拟。

图3 CS 试件滞回曲线[14]

图4 CS 侧向荷载-位移比较

1.5 有限元算例

设计了85 个C-SPW 算例，设计参数变化包括混凝土板厚度、混凝土弹性模量、内嵌钢板厚度、墙板高宽比，如表1 所列。单侧混凝土板厚度tc=40～80 mm，增量为10 mm，混凝土板厚度变化用TCx 表示；混凝土弹性模量Ec分别为25.5、30 和33.5 GPa，对应轴心抗压强度标准值13.4、20.1 和26.8 MPa 及轴心抗拉强度标准值 1.54、2.01 和 2.39 MPa，Ec变化用 ECx 表示；内嵌钢板厚度 ts=10～20 mm，增量为 2.5 mm，ts变化用TSx 表示；墙板高宽比 α 为 1.0 和 0.5，剪力墙高度 h=3 000 mm 不变，墙板宽度分别为 l=3 000 mm 和6 000 mm，l 变化用 Lx表示，栓钉水平间距 lst与垂直间距 hst相等；通过变化栓钉数量 nx×ny（nx为栓钉列数，ny为栓钉行数），改变栓钉间距sst=lst=hst=1 500 mm、1 000 mm 和750 mm，栓钉数量改变用Nx表示。设计参数的不变量为：栓钉直径dst=16 mm；混凝土板双向配筋率为0.25%；边缘框梁、柱截面分别为W530×219、W360×818。参数影响分析完成以后，取影响较大的设计参数进行分组设计，如表1 中1～15 组算例。通过有限元非线性屈曲分析得到不同设计参数下，C-SPW 屈曲对应层间侧移角与混凝土板厚关系。

2 临界层间侧移角

C-SPW 钢板剪力发展模式分为两类，取决于内嵌钢板为弹性屈曲或进入弹塑性后屈曲。通过分析钢墙板屈曲前后剪力和面外挠度的变化规律，再分析C-SPW 屈曲对应的钢板剪力和层间侧移角。以N3-TS15-TC60-EC30-L3 和N3-TS15-TC40-EC30-L3 为例说明C-SPW 屈曲时对应层间侧移角即临界层间侧移角的判别方法。二者钢墙板剪力Vs、面外挠度Dsp随层间侧移角变化的曲线如图5 所示。由图5（a）知，在弹性阶段和屈服阶段时钢板面外挠度很小；在钢板剪力有下降迹象时，面外挠度开始增大，Dsp曲线逐渐上升；θ=0.53%时，Vs曲线陡降，Dsp曲线斜率达到最大值，钢板面外挠度迅速增大；随着层间侧移角增加，Vs曲线下降速度趋于平缓，同时Dsp曲线上升速度也趋于平缓。图5（b）显示，当钢板处于弹性阶段时其面外挠度很小；在钢板剪力达到最大值前，Dsp曲线开始上升；θ=0.23%时，Vs曲线达到最大值并迅速下降，Dsp曲线斜率达到最大值，钢板面外挠度迅速增大；随着层间侧移角增加，Vs曲线下降速度趋于平缓，同时Dsp曲线上升速度也趋于平缓。

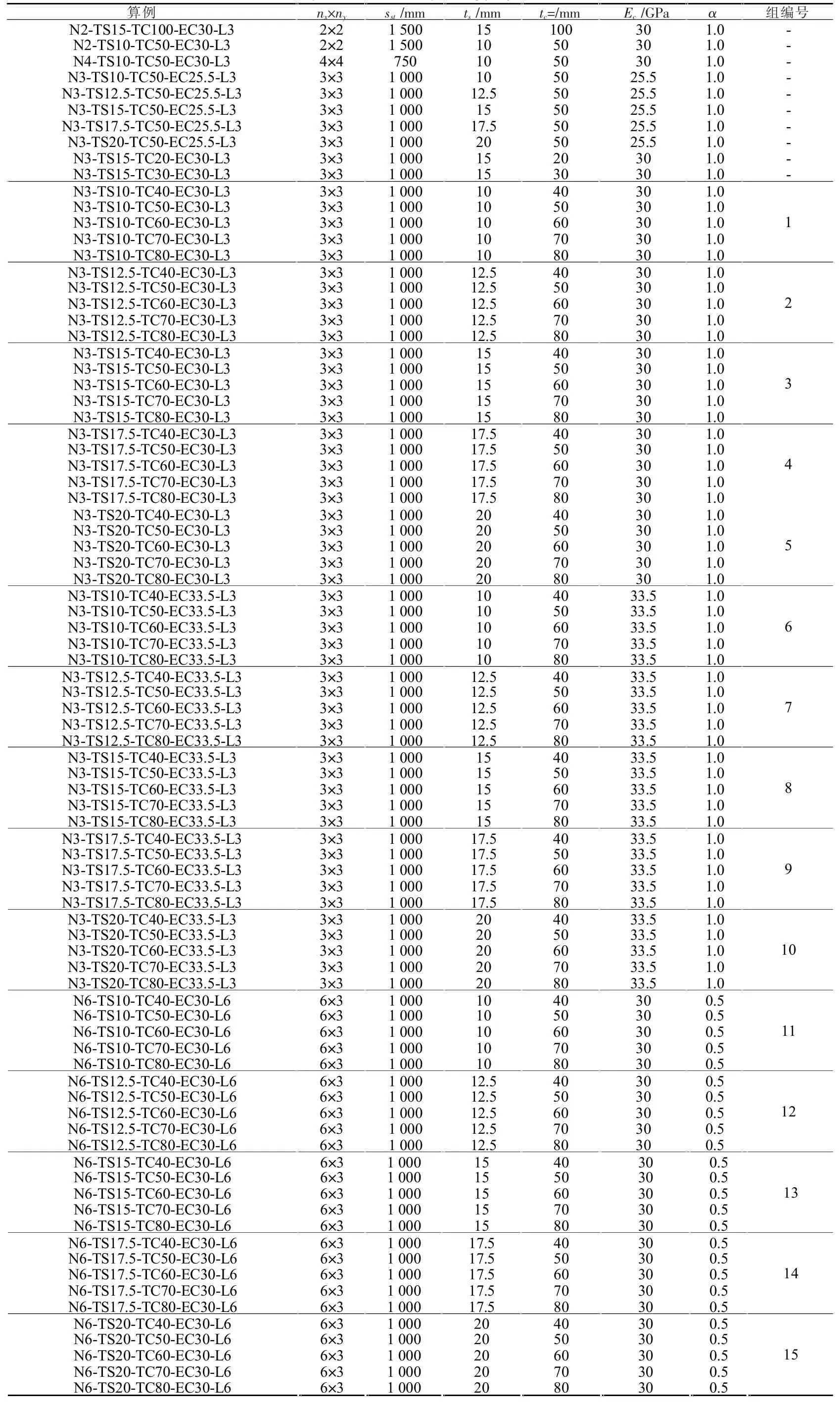
表1 C-SPW 有限元算例

图5 钢板剪力和面外挠度变化规律

比较上述两算例内嵌钢板面外挠度曲线Dsp和钢板剪力曲线Vs曲线可知，二者在钢墙板发生屈曲时曲线均出现了拐点，且Dsp随层间侧移角增加的变化规律相同。因此，钢墙板屈曲时刻通过钢板剪力和面外变形相结合进行判别。定义钢墙板屈曲对应的层间侧移角即为临界层间侧移角θb，从图5 中可以看出θb对应Dsp曲线的第一个拐点。钢墙板剪力的变化表明，图5（a）中临界层间侧移角θb对应Vs曲线平台段末尾的拐点，可见钢板已进入受剪屈服平台，发生的是弹塑性屈曲；图5（b）中临界层间侧移角θb对应Vs曲线的最大值，且该值小于钢墙板受剪屈服承载力，可见钢板处于弹性阶段，发生的是弹性屈曲。由于分析钢板剪力和面外变形曲线得到的临界层间侧移角相同，在后文研究中统一按照钢板剪力-层间侧移角曲线确定C-SPW的临界层间侧移角。

3 钢板屈曲有限元参数影响分析

3.1 混凝土板厚和弹性模量及栓钉间距的影响

不同混凝土板厚度时钢板剪力-层间侧移角曲线如图6 所示，可以看出，混凝土板厚度越大临界层间侧移角越大。钢墙板弹性屈曲层间侧移角对应的钢板剪力为钢板剪切屈曲荷载，混凝土板越厚C-SPW 受剪承载力越高；钢墙板弹塑性屈曲层间侧移角对应的钢板剪力为钢板剪切屈服承载力，混凝土板越厚，钢板受剪屈服越充分。屈曲后曲线下降趋于缓慢的阶段反映了钢墙板斜拉带形成后产生的屈曲后强度。混凝土弹性模量对下钢板剪力曲线的影响如图7 所示，混凝土弹性模量对各算例内嵌钢板受剪性能的影响相同，混凝土弹性模量越大内嵌钢板屈曲越迟缓，临界层间侧移角越大。栓钉间距变化对钢板剪力曲线的影响如图8 所示，可以看出栓钉间距越大，钢板越容易发生屈曲。

图6 N3-TS15-TCx-EC30-L3 的 Vs 曲线

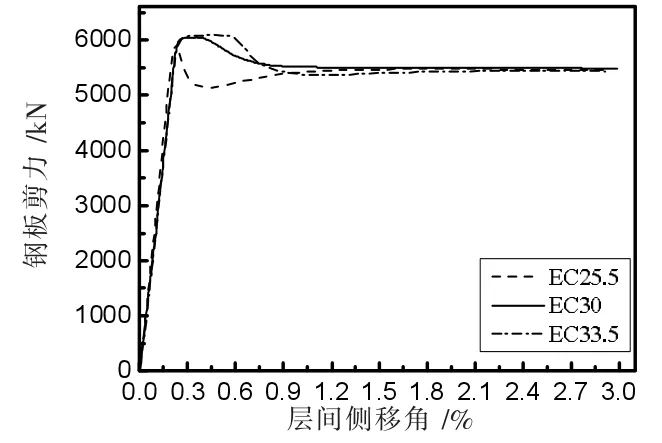
图7 N3-TS15-TC50-ECx-L3 的 Vs 曲线

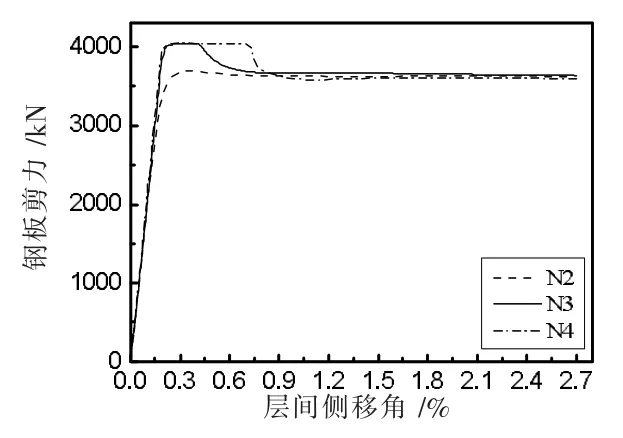
图8 Nx-TS10-TC50-EC30-L3 的 Vs 曲线

3.2 钢板厚度影响

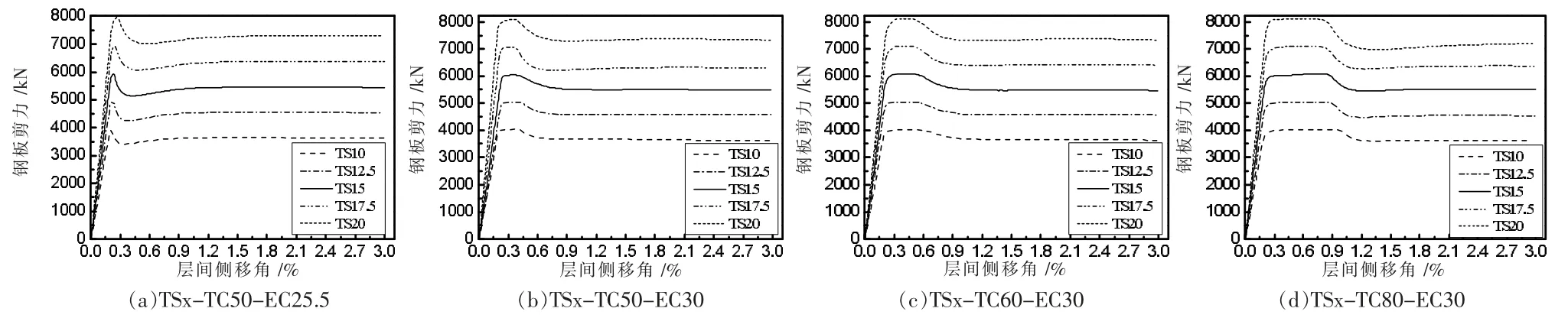
图9 N3-TSx-TCx-ECx-L3 钢板剪力Vs 曲线

内嵌钢板厚度对钢板的抗剪承载力和屈曲层间侧移角影响较大。其中，当混凝土板对钢板面外约束大小不同时，钢板厚度对屈曲层间侧移角的影响有所不同。图9（a）所示钢板发生弹性屈曲，临界层间侧移角随钢板厚度的增加而增加。图9（b）对应混凝土板面外约束相对增加，钢板发生弹塑性屈曲，各算例临界层间侧移角十分接近且钢板厚度与临界层间侧移角有由正比变为反比的趋势。图9（c）和图9（d）对应混凝土板面外约束进一步增大，临界层间侧移角随钢板厚度的增加而减小。这是由于在钢墙板屈服阶段屈曲时，钢板厚度越大，其对混凝土板横向作用力越大，混凝土板进入塑性程度越严重，面外约束能力越弱，从而导致钢墙板越早屈曲，屈曲层间侧移角减小。临界层间侧移角θb在0.28%～0.4%之间时为钢板厚度与临界层间侧移角影响关系发生改变的临界点。

3.3 墙板高宽比影响

如图10 所示，墙板高宽比对临界层间侧移角的影响与钢墙板厚度类似，均随着临界层间侧移角的增大，影响关系由正比逐渐变为反比。然而，墙板高宽比与屈曲层间侧移角影响关系的变化比钢墙板厚度影响关系变化更晚，临界点约出现在θb介于0.66%～0.97%时。屈曲层间侧移角较大时，钢墙板屈曲前混凝土板损伤已较大，钢墙板屈曲前已经与混凝土板有较小分离，高宽比小的钢板屈曲半波数量多，对混凝土板产生的横向作用力小，混凝土板面外约束劣化程度较弱，使得钢板较晚屈曲，墙板高宽比与屈曲层间侧移成角反比。

图10 N3-TS15-TCx-EC30-Lx 钢板剪力Vs 曲线

4 C-SPW变形能力要求对应的混凝土板厚需求

当C-SPW 层间侧移角到达θb后，钢墙板发生屈曲，C-SPW 承载能力开始下降，变形能力也逐渐劣化。可以认为，θb是C-SPW 层间侧移能力的上限。计算表1 中后75 个算例的临界层间侧移角，绘制临界层间侧移角随混凝土板厚度的变化曲线，为C-SPW 不同的层间侧移角变形要求提供对应的混凝土板厚。该75 个算例分为15 组，每一组算例改变混凝土板厚，各组间改变钢板厚度、混凝土弹性模量和墙板高宽比。

屈曲层间侧移角-单侧混凝土板厚度曲线（θb-tc）如图11（a）-（c）所示。由图中曲线可见，屈曲层间侧移角与单侧混凝土板厚关系近似为线性关系；曲线之间的差别随混凝土板厚的增加而增大；屈曲层间侧移角较小时各曲线差别随钢墙板厚度增加而略有增大，但屈曲层间侧移角大小相差很小，屈曲层间侧移角较大时曲线差别随钢墙板厚度增加而减小。由于钢墙板厚度与层间屈曲侧移角影响关系发生改变，曲线出现交汇处，EC30-L3 曲线交汇处在θb在0.3%左右，EC33.5-L3 曲线交汇处在θb在0.4%左右，说明影响关系改变随混凝土弹性模量增大而延后；EC30-L6 曲线未出现交汇点，说明此类算例影响关系未发生改变。

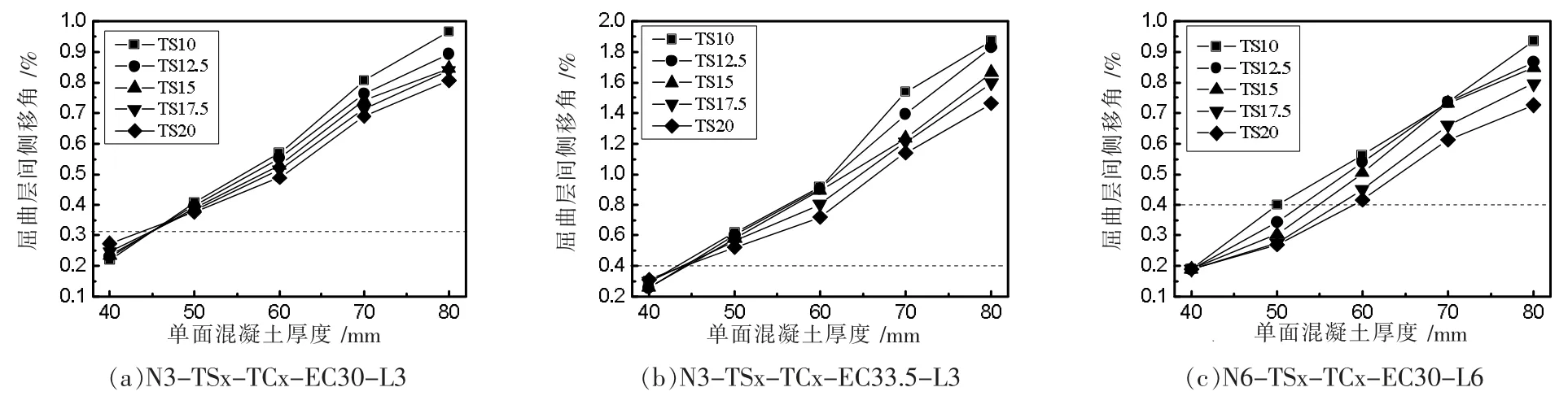
图11 屈曲层间侧移角-单侧混凝土板厚度曲线

5 结论

（1）与钢墙板发生弹塑性屈曲相比，钢板弹性屈曲对应的C-SPW 抗剪承载力更小，弹性阶段短且没有屈服平台，但钢墙板屈曲后强度不受影响。（2）当C-SPW 内嵌钢板发生弹性屈曲时，屈曲层间侧移角对应钢板剪力的最大值；当C-SPW 内嵌钢板发生弹塑性屈曲时，屈曲层间侧移角对应钢板剪力曲线平台段末端的拐点。（3）混凝土板厚度和混凝土弹性模量与屈曲层间侧移角成正比；栓钉间距与屈曲层间侧移角成反比；钢墙板厚度和墙板高宽比与屈曲层间侧移角的关系随着屈曲层间侧移角的增大由正比逐渐变为反比，后者引起变化的发生较晚。（4）屈曲层间侧移角与单侧混凝土板厚关系近似为线性关系，可依据C-SPW 层间侧移角变形要求，通过二者关系曲线得到混凝土板厚度取值。