双向蝴蝶形钢板墙-钢框架自复位结构抗震性能试验研究

孙玉康，李启才，丁志昌，张 萍，王 伟

（苏州科技大学 江苏省结构工程重点实验室，江苏 苏州 215011）

传统的钢结构一般采用构件塑性发展来耗能，例如在梁端形成塑性铰，虽然结构在震后不会因倒塌而威胁生命安全，但主体构件往往存在较大的残余变形而增加其维修成本及难度，甚至需要拆除整个建筑。为了降低主体结构的破坏程度，减小结构的残余变形，减轻地震荷载响应，方便震后维修，新型的自复位钢板剪力墙结构体系应运而生。

近十几年来，国内外学者在自复位结构理论分析和试验研究方面取得了丰硕成果。2001年，Ricles[1-2]首次提出了一种具有自复位功能的后张拉钢框架梁柱节点，随后进行了 9 个节点试件的试验，并用有限元软件模拟了试验节点。试验结果与有限元分析结果吻合，后张拉梁柱节点基本处于弹性状态，通过角钢耗散能量，基本实现自复位功能。2002年，Garlock 等[3-6]设计了一系列自复位钢框架节点试件并对其进行拟静力往复加载试验，着重研究了角钢厚度、预应力钢绞线数量和初始预应力大小等对节点复位性能的影响。该研究表明：当参数设计合理时，主体结构的梁、柱依然保持弹性状态，能量则由角钢进入塑性来耗散，震后，节点在预应力钢绞线作用下可以回复到其初始位置。2010年，Clayton[7-8]首先提出了新型的自复位钢板剪力墙结构（SC-SPSW）体系。这种新型的自复位结构体系是初始刚度和耗能能力均较好的薄钢板剪力墙和后张拉梁柱节点相结合而成的，为了达到自复位目的，要求该结构的钢框架在整个受力过程中始终保持弹性状态。该结构体系的复位功能是通过后张拉节点实现的，但其耗能并不是依靠钢框架节点处安装耗能器（如角钢）来耗能，而是利用与框架梁柱四边连接的内嵌薄钢板来耗能。2013年，Clayton 等[9-10]对两边连接（内填钢板只与框架梁连接）的自复位钢板剪力墙结构进行了理论分析和数值模拟，并对一个三层缩尺试件进行了拟静力试验。研究结果表明，与四边连接（内填钢板与框架梁、柱均连接）的钢板剪力墙-自复位结构体系相比，主要有以下优点：消除内嵌钢板对框架柱产生的附加弯矩和减轻对框架梁产生的附加轴力；减小框架柱的截面尺寸，从而也减小了用钢量，减轻对内嵌钢板墙的损伤。

2013年起，田伟、经聪、张萍等[11-13]对蝴蝶形钢板剪力墙自复位结构体系进行了一系列有限元模拟分析和少量试验研究，结果表明，该结构体系的内填开菱形孔薄钢板由拉力场受力模式转化为蝴蝶杆弯剪型受力模式，消除了薄钢板呼吸作用产生的巨大响声，提高了体系耗能能力，并且进一步减轻了内填板对主体框架的需求。为了更加有效地减轻内填板钢板的面外变形和增加耗能，本文对一个单层单跨足尺的双向蝴蝶形钢板墙自复位结构试件进行了拟静力低周往复加载试验，为该结构系的进一步研究提供相关资料。

2 试验概况

2.1 试件设计

为了保证试验自复位框架的可重复性而仅需更换蝴蝶板构件，框架梁柱应在整个受力过程中保持弹性受力状态以减少损伤，因此较实际工程而言保守设计了一个足尺的自复位钢框架。框架梁和框架柱均使用焊接 H 型钢，柱截面尺寸 H250 mm×250 mm×12 mm×16 mm，梁截面尺寸 H350 mm×220 mm×12 mm×16 mm，钢材强度等级为Q345B。柱轴线间距L=5 100 mm，层高H=3 000 mm。柱脚采用销轴形式的铰接连接。

框架梁柱连接均采用预应力自复位节点，即沿梁腹板两侧对称布置6 组通长预应力钢绞线，每组由三根直径为15.2 mm 的钢绞线组成，每组钢绞线设计的初始预应力为165 kN。通过圆柱型锚具预应力钢绞线固定在框架柱外翼缘加强板处，且在一侧（西侧）锚具处安装压力传感器来监控预应力施加和试验过程中预应力的变化规律。

内填双向蝴蝶板采用Q235B 钢，强度低于框架梁柱的Q345B 钢，以增加其延性和耗能并减小墙板对框架的作用，厚度为10 mm。为了防止墙板过早发生面外失稳，在其两侧和中间分别通过高强螺栓连接了两根槽钢（140 mm×55 mm×4 mm，长度为 2 400 mm）。内填钢板通过上下各两根角钢（L110 mm×110 mm×10 mm，长度为2 100 mm）与框架梁用10.9 级高强度螺栓连接。双向蝴蝶板详图如图1 所示，试件详图如图2 所示。

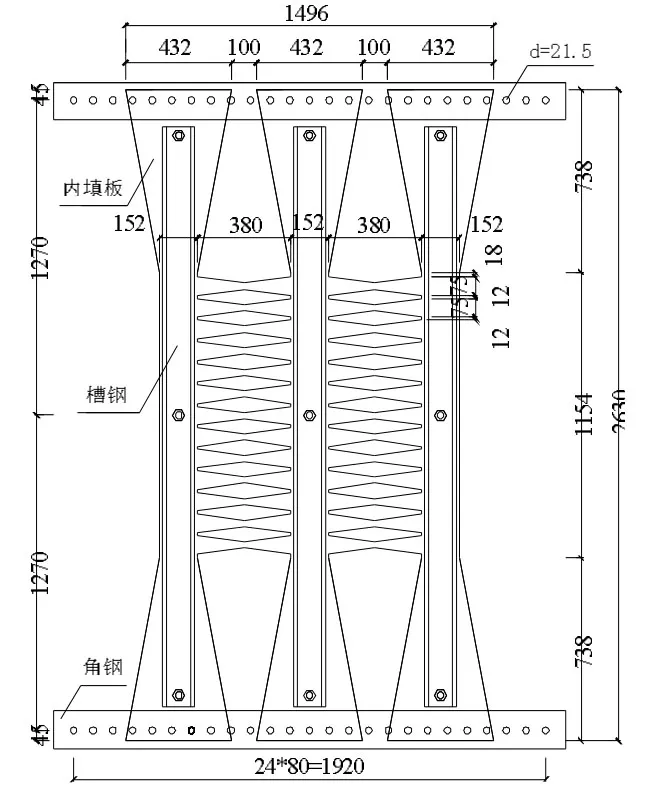
图1 双向蝴蝶板详图

图2 试件详图

2.2 材性试验

材性试验为单向拉伸试验，按照《钢及钢产品力学性能试验取样位置及试样制备》（GB/T 2975-2018）[14]和《金属材料拉伸试验第1 部分：室温试验方法》（GB /T228.1-2010）[15]的规定方法进行了材性试验。依据所用钢材厚度（10、12、16 mm）的不同，分为 3 组，分别命名为 S-10、S-12 和 S-16，每组均制作 3 个试件。结果如表1 所列。

表1 钢材材料性能

2.3 试验加载装置和加载制度

本次试验采用最大轴向力为1 000 kN 的作动器对自复位钢框架进行加载。作动器的一端与反力墙铰接，另一端则和加载梁铰接连接，加载梁与顶梁通过高强度螺栓连接。加载过程中，为避免试件发生面外失稳，在加载梁处设置了两道平面外侧向支撑。试验加载装置示意如图3 所示。

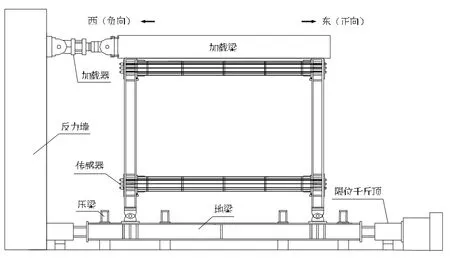
图3 试件加载装置图

该试验全程采用位移控制，通过参考美国SAC（1997）[16]规范进行加载。首先进行预加载，待确定数据读取正常后，再开始正式加载。加载级共有六级，试件整体位移角分别为0.375%、0.5%、1%、1.5%、2%和3%，对应的位移分别为 14 mm、19 mm、34 mm、54 mm、75 mm 和 113 mm，每级加载循环次数分别为 6 圈、6 圈、4圈、2 圈、2 圈和 2 圈。

2.4 测点布置

试件位移计、应变花和压力传感器布置见图4。为了得到框架的的整体位移角，布置位移计DT2、DT11、DT6 和DT12；为了得到试件层间位移角，布置位移计DT10、DT11、DT12 和DT13；为了得到梁柱节点的转角变形，布置位移计DT3、DT4、DT7 和DT8；为了得到地梁的滑移量，布置位移计DT1。因为加载梁的存在，无法在顶层梁上翼缘处布置位移计。在梁柱节点区、内填蝴蝶板和预应力钢绞线锚固处布置应变花来监控这些部位应力发展状况。为了获得试件在整个加载过程中每组钢绞线预应力的变化情况，在其左侧（西侧）锚固处分别布置一组压力传感器（LC1～LC12），共计12 个。

图4 位移计和应变花布置图

3 试验现象

根据不同加载级，对试验现象进行描述。

在第一加载级（位移角为0.375%）和第二加载级（位移角为0.5%）时，梁柱节点处的压力传感器和位移计数值基本没有变化，且钢框架无明显现象，表明节点没有打开，从后面的滞回曲线也可以看出，内填双向蝴蝶板几乎没有发生面外变形，此时试件基本处于弹性受力状态。卸载后，试件可实现完全复位。

在第三加载级（位移角为1%）加载时，梁柱节点开始打开，节点处位移计显示数数开始有变化，钢绞线预应力值增加明显，蝴蝶杆的面外变形有微小的弯曲变形。试件开始出现间断的响声，观察发现是内填板与框架梁连接处出现拉拔现象，螺栓发生滑移产生的，如图5 所示。

在第四加载级（位移角为1.5%）和第五加载级（位移角为2%），梁柱节点打开更加明显（见图6），节点处上下两组钢绞线预应力值不断增大且变化一致，说明梁柱节点脱开具有一致性。内填双向蝴蝶板中竖向蝴蝶杆在槽钢的限制下几乎没有发生面外变形，而横向蝴蝶杆弯曲变形较为明显（见图7）。

加载到第六加载级（位移角为3%位移角）时，蝴蝶杆没有发生撕裂破坏，槽钢没有变形，内填板与框架梁的拉拔现象加剧，试件的承载力一直在增加。试验前墙板和试验后墙板分别如图8 和图9 所示。

图5 墙板及螺栓滑移

图6 蝴蝶杆弯曲变形

图7 节点打开

图8 试验前墙板

图9 试验后墙板

4 试验结果分析

4.1 试件滞回曲线

为了研究双向蝴蝶形钢板墙-钢框架自复位结构的抗震性能，通过整理试验位移计数据，得到该试件的层间滞回曲线和和一个节点转角滞回曲线，分别如图10 和图11 所示。

通过对层间和节点滞回曲线进行分析，可以得到如下结论：（1）当试件在前两个加载级（即0.375%和0.5%）时，水平荷载较小，节点的转动变形主要是来自于梁柱的弹性变形，此时的内嵌蝴蝶板基本处于弹性状态，只有很小一部分进入塑性耗能。卸载后，几乎没有残余位移角，结构基本实现了完全复位。（2）当试件再进行逐级加载时，随着水平荷载的增加，滞回环展开并且包含的面积不断增加。卸载时，残余位移角也不断增大。（3）直到最大层间位移角3%时，试件的承载力一直在增加，未出现承载力退化。正向承载力最大值为448.06kN，负向承载力最大值为479.43 kN，正负向承载力的细微差别可能是系统摩擦和正负向推拉时内嵌蝴蝶板的塑性变形、面外屈曲等原因产生的。（4）试件的层间位移角大于相应的节点转角，这是因为试件的层间变形主要来自于节点的转角变形和钢框架整体的剪切变形。

图10 层间滞回曲线

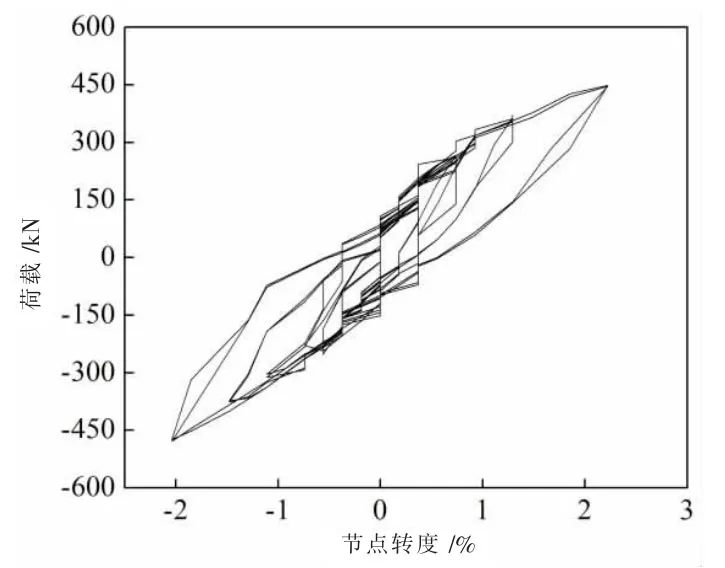
图11 节点滞回曲线

4.2 试件耗能

结构耗能能力是评价其抗震性能的一个重要指标，在荷载-位移曲线上，滞回环所包围的面积代表结构的耗能，面积越大，表示能量耗散越多。它实质上表示结构吸收地震能量后转化为其他非弹性变形能量的部分。该试件的耗能主要是由内填双向蝴蝶形钢板构件提供的。本次试验结构的耗能能力是通过耗能量和能量耗散系数来描述的，分别如图12 和图13 所示。

通过对耗能量和能量耗散系数进行分析，得到如下结论：（1）在前两个加载级，试件耗能非常小，基本处于弹性受力状态，结构的微小耗能可能来自于系统的摩擦等。（2）随着内填钢板进入塑性的程度愈来愈大，耗能能力也不断提高。（3）试件的耗能量随着位移角的增大而增加，而能量耗散系数在位移角为1.5%时达到最大值，随后略有降低。原因是在位移角1.5%之前，内填蝴蝶板主要是平面内塑性发展越来越充分，使能量耗散系数愈来愈大；位移角1.5%之后，横向蝴蝶杆平面外的弯扭变形不断发展，使得试件的耗能能力下降。

4.3 试件残余变形

结构残余变形的变化规律，不仅可以反映结构的损伤进程，而且是评定自复位结构复位功能的关键指标。传统钢框架在震后具有较大的残余变形，这主要是主体构件梁柱发生的塑性损伤造成的，而内嵌蝴蝶形钢板的自复位钢框架的残余变形，是蝴蝶板（作为耗能器）在发生塑性变形产生的永久变形。本试验从残余层间位移角和残余节点转角两个方面考察结构的残余变形，分别如图14 和图15 所示。

通过对残余层间位移角和残余节点转角进行分析，可以得到如下结论：（1）当结构处于前两个加载级（即位移角为0.375%和位移角为0.5%）时，由于基本处于弹性阶段，层间残余位移角和残余节点转角均几乎为零。（2）随着位移角的增加，墙板进入塑性耗能阶段，残余变形变化趋势一致，且正向和负向残余变形基本对称。（3）在整个加载过程中，试件的残余变形随着位移角的增加而不断增加。在位移角为3%时，正向加载的最大残余层间位移角为1.09%，最大残余节点转角为0.57%，负向加载的最大残余层间位移角为0.94%，最大残余节点转角为0.54%。复位效果并不理想，这主要是由于钢框架柱尺寸设计偏小，导致框架柱出现弯曲变形，内填钢板板较厚，反向加载时存在较大的残余压力，且经多次试验后在梁柱节点区发生局部剪切屈服损伤造成的，这也表明当梁柱节点进入弹塑性阶段，对结构的复位性能影响很大。

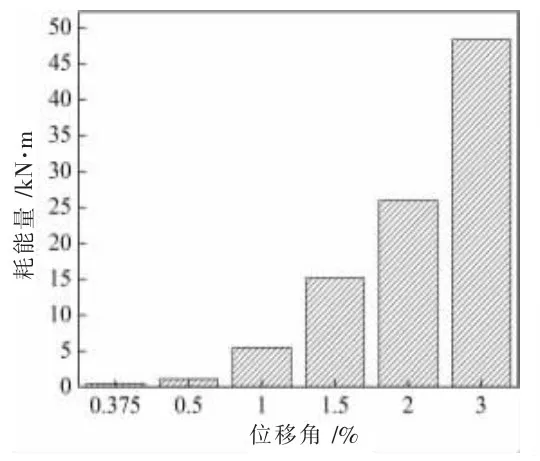
图12 耗能量

图13 能量耗散系数

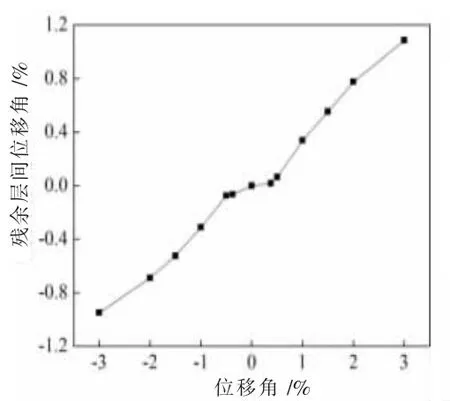
图14 残余层间位移角

图15 残余节点转角

4.4 梁柱Mises应力

分析应变片得到的几个典型测点的Mises 应力如图16 所示，通过分析图16 可以得出：所列测点Mises应力均小于相应的钢材的屈服强度，表明框架梁柱在测点处处于弹性受力状态；Mises 应力随水平荷载呈现规律变化，有些呈现明显的对称性，但大部分测点正负向并不对称。

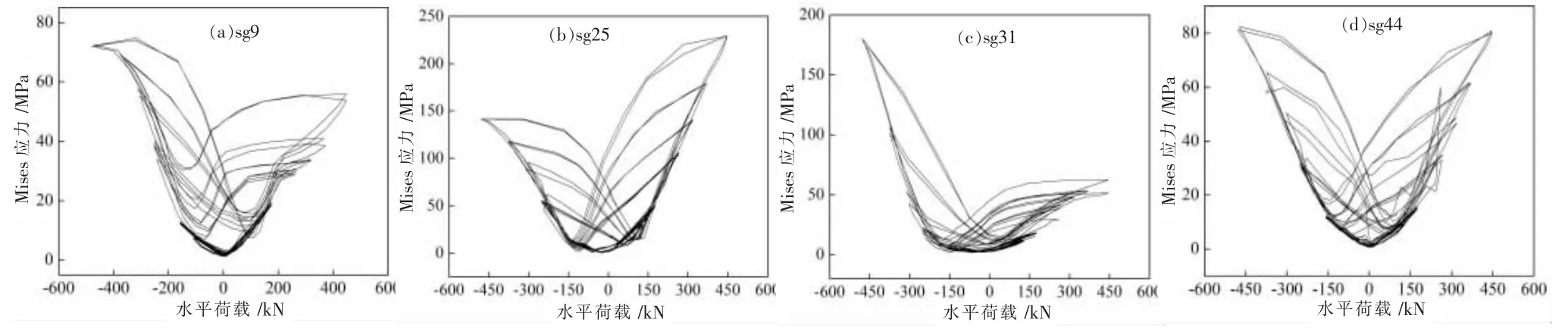
图16 测点Mises 应力

4.5 内嵌蝴蝶板应变分析

试件的内填双向蝴蝶板2 个测点的整体剪应变和前期（前两个加载级）剪应变随水平荷载变化曲线如图17 所示，sg53 为内填板横向蝴蝶杆腰部测点，sg48 为内填板竖向向蝴蝶杆端部测点。通过分析图17 可以得出：（1）在加载前期横向蝴蝶杆腰部呈现为平面内剪切变形，且剪应变对称变化，但随着加载的继续，面外变形程度加大，受力性质发生了改变，其剪应变变化失去规律。（2）竖向蝴蝶杆端部由于贯通板带的约束，其变形受到制约。在加载前期，其剪应变呈现一定程度的对称变化，但随着加载的继续，端部的面外变形越来越大，其剪应变变化也失去规律。

图17 蝴蝶杆剪应变

4.6 预应力曲线

预应力-位移角曲线中每层梁的预应力值取其6 股钢绞线预应力的平均值。试件的预应力曲线如图18 所示，从中可知：（1）当位移角小于0.5%时，预应力值几乎无变化，这也验证了在前两个加载级，试件基本处于弹性状态，梁柱节点没有打开。（2）随着加载的进行，节点打开，钢绞线被拉长，预应力随着位移角的增大而基本呈线性增加。（3）每层梁钢绞线的预应力损失很小并且始终处于弹性状态。（4）预应力-位移角曲线正向和负向并不对称，底梁的正向预应力值大于负向预应力值，而顶梁的正向预应力值小于负向预应力值。

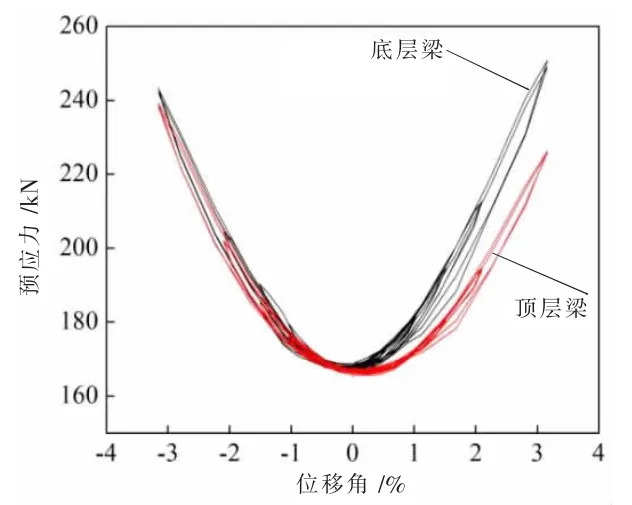
图18 预应力-位移曲线

5 结论及建议

本文通过对一榀足尺双向蝴蝶形钢板墙-钢框架自复位结构抗震性能的试验研究得出如下结论：

（1）双向蝴蝶形钢板墙-钢框架自复位结构具有较好的承载力、变形能力和耗能能力。

（2）试件由于自复位框架柱抗弯刚度偏小及梁柱节点在局压作用下发生了弹塑性损伤，影响了体系的复位功效，但依然有效控制残余变形的发展。试验可为实际工程提供参考，即梁柱节点区应局部增强以提高其抗局压能力，如梁柱节点区焊接钢板形成封闭截面且相应增加框架柱截面，使得框架与蝴蝶板具有一致的初始刚度，从而实现结构耗能与复位的有机统一。

（3） 连接双向蝴蝶形钢板墙与框架梁的高强螺栓在水平荷载较大时会出现了一定滑移，影响了试件性能的发挥，需要采取应对措施来避免或延缓螺栓的滑移。