基于GFRP加固的RC梁柱结构抗连续倒塌性能研究

钱 爽，范存新

（苏州科技大学 土木工程学院，江苏 苏州215011）

连续倒塌是建筑结构由于自然因素或者恐怖袭击等人为因素引起的偶然荷载作用，造成结构关键部位的破坏而引起的连续反应造成结构周边构件破坏，最终使结构不成比例倒塌和整体倒塌[1]。进入21 世纪后，印度新德里大楼倒塌事故与巴西三座办公楼倒塌事故等再次引起人们对结构连续倒塌的关注，使世人更深入的研究抗连续倒塌过程，并采用新材料与新工艺加固房屋结构来抵御结构的连续倒塌破坏。

针对结构抗连续倒塌问题，国内外发布相关的规范有GSA2003[1]、ASCE7-05[2]、DoD2010[3]、《混凝土结构设计规范》（GB50010-2010）和《建筑抗震设计规范》（GB50011-2010）。诸多学者也进行了大量相关方面的研究，如Ortont[4]等研究发现不同种类的纤维聚合材料FRP 都可提高RC 梁柱结构在连续倒塌悬链线阶段的承载力。秦卫红等[5]通过试验验证了GFRP 布可以有效提高结构的抗连续倒塌承载力。丁智等[6]研究了CFRP 与AFRP 加固RC 梁的受弯性能。Maalej 等[7]研究了RC 梁的尺寸、FRP 布的加固层数以及FRP 与混凝土之间的界面粘结力对加固效果的影响。易伟健等[8]通过连续倒塌试验研究连续倒塌过程中的钢筋变化规律与抗连续倒塌机制的发展过程。Yu 等[9]通过两个二分之一的梁柱子结构研究抗震配筋对结构抗连续性能的影响。Jinkoo 等[10]研究了用不同钢板和高强绞线加固预制装配式梁柱结构的抗连续倒塌性能。初明进等[11]等研究了考虑楼板的RC 梁在不同梁高，配筋情况下的抗连续倒塌性能。P.X.Dat 等[12]研究了不同配筋下板薄膜效应对结构抗连续倒塌的作用。姚远等[13]研究梁上部钢筋跨中布置方式提升结构抗倒塌能力的效果。

GFRP 材料具有轻质高强、耐腐蚀、与钢筋连接性好、极限变形能力优于其他FRP 等特点，因而符合结构加固材料对延性的要求[5]。前述研究也表明了钢筋在结构抗连续倒塌中的重要作用，无论受弯还是受拉阶段皆依靠梁内通长纵向受力钢筋提供承载力，但在文献[5]中仅研究了GFRP 材料对梁下部钢筋进行加固的效果，而未研究采用GFRP 材料加固梁上部钢筋的效果。在文献[13]中通过研究梁上部钢筋跨中布置方式发现梁上部受压钢筋在大变形受拉阶段开始受拉，梁抗连续倒塌最终承载力要考虑梁上部钢筋所做的贡献才更符合实际情况。因此本文综合文献[5]和文献[13]的研究成果，对梁上部钢筋采用GFRP 加固后结构抗连续倒塌性能进行了研究。本文设计了梁上部钢筋截断模型（A1）与梁上部钢筋截断且用GFRP 布纵向加固模型（A2）。通过数值模拟软件OpenSees 基于位移控制模拟抗连续倒塌过程，分析GFRP 布加固后的结构位移荷载曲线、截面应力趋势、以及轴力位移曲线，研究梁上部钢筋采用GFRP 加固后抵抗连续倒塌的效果。

1 连续倒塌的抗力机制

RC 梁柱结构连续倒塌模型如图1（a）所示。RC 梁柱结构在外荷载P 的作用下出现变形，依赖自身内部抗力来抵抗外荷载P。当梁柱结构发生连续倒塌时，失效柱所在位置处的位移-荷载曲线如图1（b）所示。因为每个阶段结构内部抗力产生的原因不同，将整体结构抗连续倒塌机制分为梁机制与悬链线机制[14-15]，倒塌过程分为三个阶段：

（1）梁机制阶段：梁在失效柱处外荷载P 作用处于受弯阶段。梁在点A 之前只是弹性弯曲变形，主要靠梁截面的抗弯能力来抵抗外荷载P 的作用。但是随着失效柱位置处竖向位移持续变大，此处梁下部受拉区混凝土逐步开裂，使得梁截面中的中性轴上移。与此同时支座处由于受到负弯矩的作用，表现为上部受拉应力而下部受压应力的作用，使得支座处梁上部混凝土受拉开裂，其梁截面位置处的中性下移，中性轴因此不在一水平面上。之后由于内部失效柱两侧剩余的结构完好能够同时提供轴向约束，则结构会形成类似拱的作用从而在梁内部形成压拱效应继续提升梁机制抗力，梁机制后期结构抗力由截面的抗弯承载力与压拱效应共同提供。最后当梁端弯矩达到塑性铰弯矩时，梁柱节点塑性铰区混凝土压坏，梁机制达峰值作用点B。梁机制时结构受力作用图如图2 所示。

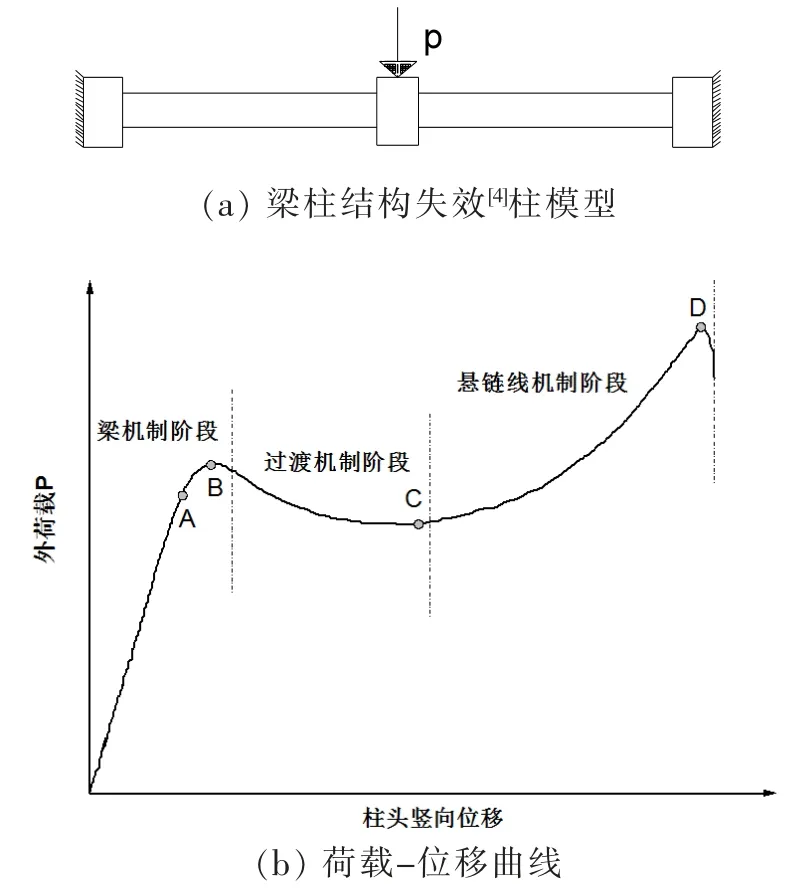
图1 结构连续倒塌模型

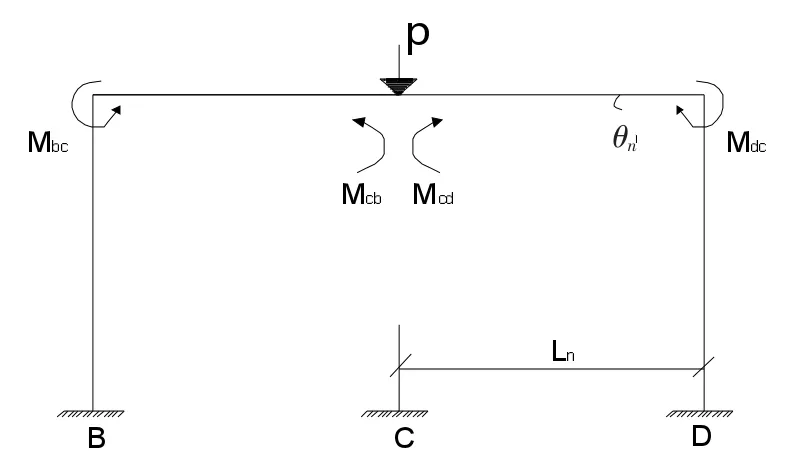
图2 梁机制时受力[5]作用图

梁机制作用阶段承载力根据极限塑性铰弯矩理论[15]计算,选取选取第一层横向一榀4 跨失效柱所在的梁柱子结构进行受力分析，具体选用中间两跨进行受力分析。并因BC 梁与CD 梁在结构上是对称的，根据结构力学可知梁两端对称部分的弯矩相等，有Mcb=Mcd与Mbc=Mdc，从而梁机制抗力公式如下

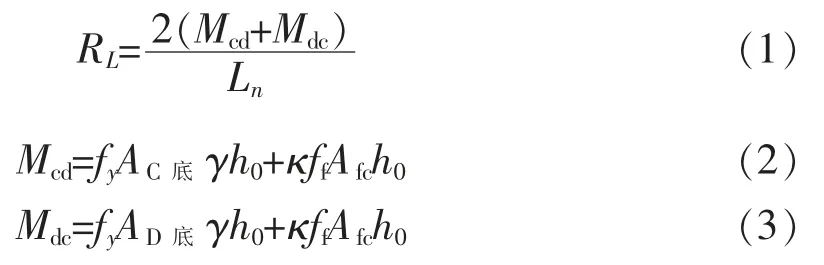
式中，Mcd和 Mdc为梁端峰值塑性铰弯矩，fy为钢筋屈服强度，AC底为 C 端底部全部受拉钢筋面积，AD底为 D 端顶部全部受拉钢筋截面总面积，κ 为GFRP 布有效强度因子调整系数，ff为GFRP 抗的拉强度设计值，Afc为GFRP 布实际宽度与厚度的乘积，Ln为单跨梁长度，γ 为内力臂系数，h0为梁截面有效高度。

（2）过渡机制阶段：加载到点B 之后是梁机制与悬链线机制共同作用阶段。RC 梁柱结构中混凝土的裂缝随变形增大，从而梁端转角θn变大，在梁端转角θn数值较小时梁机制抗力起的作用大。在梁机制阶段，结构主要靠梁截面的抗弯能力和压拱效应来抵抗外荷载P 的作用。而当梁端转角θn较大时，悬链线机制抗力起的作用更大。因为悬链线机制阶段抗力主要有梁中钢筋承担，且根据受力分析可知随着梁端转角的变大而增大。当裂缝贯穿整个混凝土截面时（C 点），能够产生压应力的未开裂混凝土面积变小使得梁机制作用退出工作，连续倒塌抗力完全由RC 梁中的纵向贯通钢筋和用GFRP 加固的截断钢筋提供（针对加固模型A2）。

（3）悬链线机制阶段：进入悬链线机制阶段后，结构承载力随着竖向变形的增大再度变大，原先受压的钢筋也逐渐由受压转变为受拉。悬链线机制阶段抗力主要由梁内纵向受拉钢筋以及GFRP 布提供。当梁内纵向受力钢筋拉断之后，RC 梁柱结构发生倒塌使得结构内部的承载力迅速减小。直至RC 梁柱结构完全丧失承载能力之后进入倒塌破坏状态。悬链线机制受力作用图见图3。

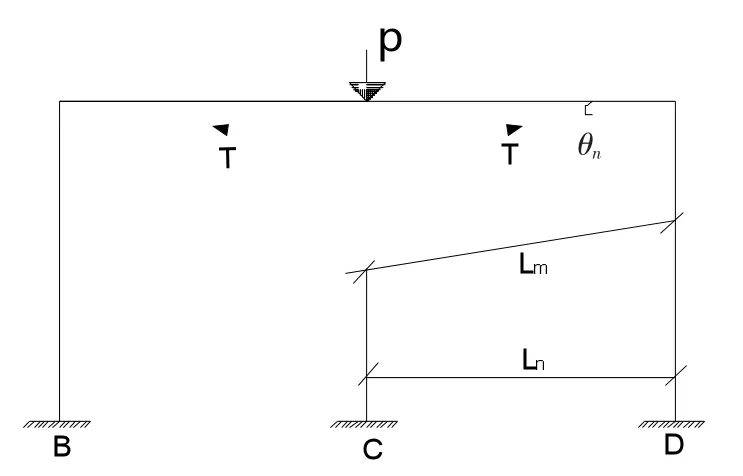
图3 悬链线机制时[6]受力作用图

因为悬链线机制阶段抗力主要有梁中受拉钢筋与梁底部纵向GFRP 布承担，因此结构的悬链线机制抗[7]力的公式如下

式中，T1为钢筋[8]拉力，T2为 GFRP 布提供的拉力，φ 为钢筋应力变化不均匀系数，K 为一跨受拉钢筋数量，fymax为钢筋极限受拉强度，As为单个受拉钢筋截面面积，θn为梁端转角，κ 为GFRP 布有效强度因子调整系数，ff为GFRP 材料的拉强度设计值，Afc为GFRP 布实际宽度与厚度的乘积，Ln为单跨梁长度，Lm为单跨梁变形后长度。

2 数值模拟模型的验证

2.1 数值模拟方法

为了更接近真实模拟RC 梁上部钢筋截断与梁上部钢筋截断之后用GFRP 加固两种模型，比较加固前后的效果。本文用数值模拟软件OpenSees 进行分析研究。首先截面选取的是基于柔度法的纤维截面模型，单元模型选取基于柔度法的分布塑性单元FB[16]作为非线性梁柱单元，单元FB 的非线性反应是Gauss-Lobatto积分点的函数，并通过Coleman 等基于能量原理的修正积分后来描述材料应力应变的关系，可用来模拟模型中存在截面软化材料，进而更好的在曲线中的体现出下降段。具体的的单元划分为钢筋纤维，外围无约束混凝土纤维，核心约束区混凝土纤维，对于GFRP 材料加固的模型，还要多上GFRP 布纤维。其中核心混凝土采用矩形单元，外围无约束混凝土采用梯形单元，钢筋采用点单元，而GFRP 布则采用矩形单元。并由文献[16]知当截面纤维划分到一定数量时，划分再细对计算精度的影响就不大了，因此本文的单元划分数目为50 个。本文混凝土材料选择基于Scott-Kent-Park 基础的Concrete02 本构，分为约束区和约束区计算；钢筋选用Hysteretic 本构；GFRP 材料则选用ElasticPP 本构： 对于梁柱单元的分析分别采用Corotational 法和PDelta法；采用考虑能量原理的牛顿迭代算法，并用拉格朗日方法进行边界条件的施加；最后基于位移控制法在失效柱位置施加集中荷载进行几何非线性Pushdown 分析。

2.2 验证结构抗连续倒塌性能试验

本文研究以秦卫红等[5]的GFRP 加固RC 结构抗连续倒塌试验中的UL1 试件作为验证对象，UL1 试件的特点是梁底部钢筋在中间节点区贯通且通长拉直。梁柱子结构为2 跨且每跨2 000 mm，混凝土等级为C30，混凝土[9]保护层厚度为10 mm，梁柱纵向钢筋采用HRB400，箍筋采用HPB235。梁端和受剪切区域箍筋配筋充足可以承受内部剪力，梁柱配筋满足抗震设计规范的要求。构件图见图4，秦卫红等[10]试验所用材料性能参数见表1。

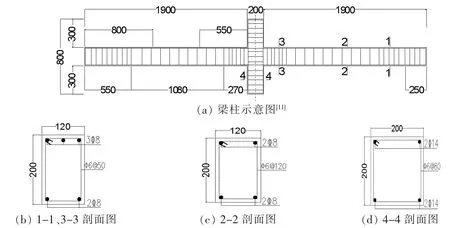
图4 试件立面图

表1 材料性能表

通过数值模拟软件OpenSees 得到失效中柱位移与荷载的曲线，模拟结果与UL1 试件的试验数据如图5所示。可以从试验模型和模拟模型梁机制峰值点G1为31.7 kN，G2为 32.1 kN 看出梁机制峰值点接近[12]，且梁机制阶段模拟数据与试验数据基本吻合。其后随着变形的继续发展，梁柱节点区域形成塑性铰区域。由于两侧梁柱相对完好可以提供充足轴向力，因此可以进入压拱阶段出现第一个下降段，模拟曲线也能很好的还原出下降段的走势。最后随着变形增大，逐渐进入大变形阶段即悬链线机制阶段，此时数值模拟曲线与试验曲线都重新进入上升段，悬链线阶段峰值H2为37.6 kN，H1为 36.5 kN。可以看出 H1与 H2的值相差不大，存在的差距可能是模拟与试验由于选取的材料本构关系与试验数据之间的误差造成的。但是模拟曲线与试验曲线在整个连续倒塌过程中的趋势与数值是接近的。因此证明本文运用OpenSess 的模拟方法是可行的。

图 5 荷载-位移曲线

3 RC梁上部钢筋采用GFRP布加固抗连续倒塌性能研究

3.1 数值模拟模型

为了研究RC 梁上部钢筋采用GFRP 布加固抗连续倒塌性能，本文按照《混凝土结构设计规范》与《建筑抗震设计规范》的要求通过PKPM 设计了一个抗震设防烈度为7 度的5 层的RC 框架结构，首层高3.2 m，标准层高均为3 m，并布置高1.3 m 的基础相连层，跨数为横向4 跨，纵向6 跨，跨度均为3 m。RC 框架结构的标准层平面布置图见图6，三维透视图见图7。

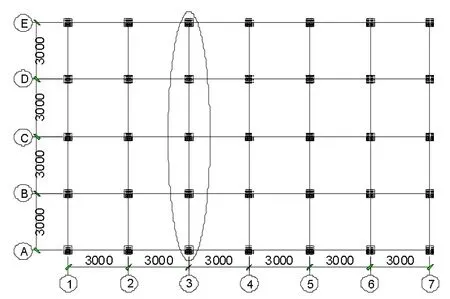
图6 标准层平面布置图

结构设计参数如下：设计地震分组为为第一组，场地类别二类，框架柱截面尺寸为400 mm×400 mm，梁截面尺寸为250 mm×400 mm，框架梁柱的混凝土等级为C30，框架梁柱的纵向受力钢筋与纵向分布钢筋均采用HRB400，梁柱箍筋也采用HRB400，梁柱砼保护层厚度20 mm，框架梁端负弯矩调幅系数为0.85，基本风压值为0.5 kN/m2，通过计算施加的恒活荷载均为2.0 kN/m2，地面粗糙度类别为B 类，体型系数为1.3[13]。钢筋材料性能指标选用的是何庆峰等[17]所做试验数据，因其试验考虑悬索作用与本文采用GFRP 布加固提高结构整体抗拉作用有相通之处，材料性能参数如表2 所示，后文公式计算选用的也是表2 材料参数。

表2 材料性能表

为模拟结构的连续倒塌过程，如图6 选取第一层横向一榀4 跨梁柱子结构进行数值模拟分析，不考虑板的影响。运用OpenSees 数值分析软件中的结构分析模型A1 与A2 分别如图8（a）与图8（b）所示。按规范设计要求梁上部钢筋在跨中1/3 位置处截断，而本文的主要研究是梁上部钢筋用GFRP 加固后对结构抗连续倒塌性能影响。因此设置中柱为失效柱，设计了A1（梁上部钢筋截断） 与A2（梁上部钢筋截断基础上用GFRP 部纵向加固） 两个模型，其中A2 在A1 基础上梁的上下表面分别用一层GFRP 布纵向加固，梁纵向GFRP 宽度为250 mm。设置的GFRP 环形箍间距是300 mm，宽50 mm。单层GFRP 布厚度为0.169 mm，A1与A2 梁柱截面模型如图8（c）所示。

3.2 数值模拟分析

3.2.1 梁柱子结构失效柱处承载力分析

本处模拟选用的建模方法，材料本构关系以及截面单元划分准则都与前文模拟FRP 加固梁柱的钢筋混凝土框架抗连续倒塌性能研究中的UL1 试件相同。在跨中失效柱的顶部施加竖向集中荷载P，基于位移控制进行加载,迭代步长选取0.001 m，对A1 与A2 进行抗连续倒塌模拟分析。通过数值模拟分析可分别得到A1 与A2 失效柱节点处的位移-荷载曲线，位移-轴力曲线分别如图9 与图10 所示，其中图10 中正值表示拉力，负值表示压力。

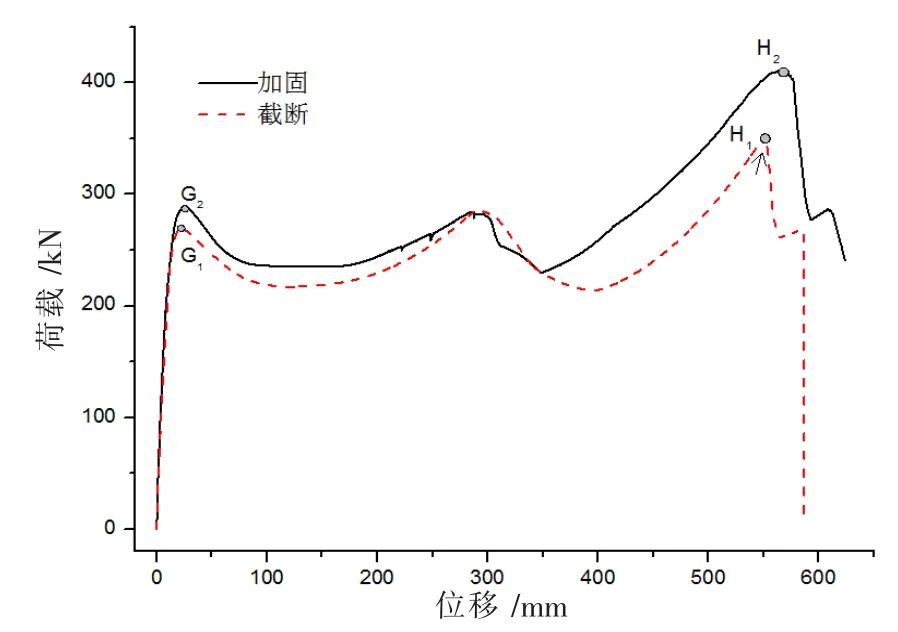
图9 位移-荷载曲线

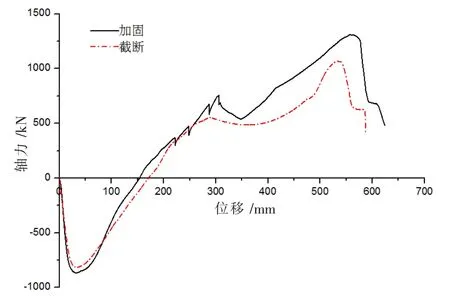
图10 位移-轴力曲线

从图9 和图10 模拟曲线综合来看，A1 与A2 均完整的经历了小变形梁机制阶段与大变形悬链线机制阶段，前期梁机制阶段[14]，框架梁主要靠整体的抗弯能力抵抗变形的发展。随着变形的增大，A1 与A2 曲线分别达到梁机制作用的峰值点G1与G2[15]，梁内部轴压力也达到最大值，梁中塑性铰区完全形成，梁端弯矩数值达到塑性铰弯矩后受弯阶段结束。受弯阶段结束后随着位移的增大，A1 与A2 逐渐进入复合机制阶段，此时结构从梁机制向悬链线机制转变。由于模型两端的固定约束可以有效限制水平位移为梁提供轴向约束因而存在压拱效应。当梁裂缝向受压区扩展使承受压应力的混凝土区域缩小，压拱作用逐步减弱。之后随着竖向外荷载的继续作用使得裂缝发展到整个混凝土受压区，当受压区混凝土达到极限压应变后逐渐压碎脱落失去作用，梁内部受力由轴压力转变为轴拉力且压拱效应完全失去作用。随着梁中轴拉力随着梁端转角增大而增大，梁中抗力由弯矩与压拱效应共同提供转变由拉力提供，A1 与A2 进入悬链线机制阶段。A1 与A2 悬链线机制作用的峰值分别在H1与H2达到[16]，梁内部的轴拉力达到最大值。可以看出梁机制阶段A1 与A2模型的抗倒塌能力较为接近。而在悬链线机制阶段，A2 比A1 具有更大极限抗倒塌荷载以及竖向变形。

按照经典弹塑性理论，根据公式（1）与公式(4)可以分别计算出A1 与A2 模型的梁机制峰值承载力和悬链线机制峰值承载力分别如表3 和表4 所示，其中FLj和FLm分别表示梁机制峰值承载力的计算值与模拟值，FLj和FLm分别表示悬链线机制峰值承载力的计算值与模拟值[8]。

表3 梁机制峰值承载力

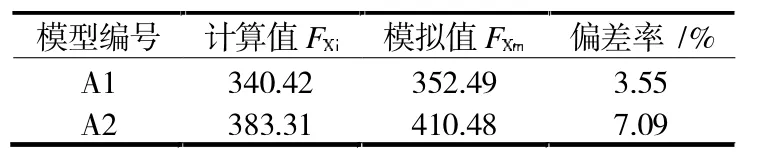
表4 悬链线机制峰值承载力

并可以通过表3 与表4 看出数值模拟值与理论计算值偏差不大，因此可以知道模拟效果较好。存在的偏差是由于数值模拟本构关系与实际结构的材料本构存在出入。因截面测点应变模拟数值可以较好地描述梁机制阶段承载力的变化趋势，后文将结合梁关键截面应力发展情况，阐述梁上部钢筋采用GFRP 布后抵抗连续倒塌的效果。

3.2.2 梁关键截面应力分析

梁机制作用阶段截面S1、S2 分别承受正弯矩（上部压应力下部拉应力）、负弯矩（上部拉应力下部压应力） 作用。而发展到悬链线机制阶段后梁全截面受拉力作用。如图11 和图12 所示，通过数值模拟软件OpenSees 分别选取梁截面S1、S2 的上下部测点分析应力的变化趋势。

由图11 和图12 综合来看，梁关键截面S1 处（见图11），A1 与A2 梁底部构件一直处于受拉状态，而A1与A2 梁顶部构件在梁机制阶段受压，后分别在325 mm 与250 mm 左右开始进入悬链线受拉阶段。在悬链线机制阶段，A1 模型主要靠钢筋承受拉应力，而A2 模型依靠钢筋与GFRP 布共同作用承受拉应力。并且由于失效柱处弯矩最大，有应力集中现象，梁底部受拉钢筋先于上部钢筋破坏。由于GFRP 材料与钢筋的适应性较好，A2 模型梁上下部表面用GFRP 布进行纵向加固可以间接提高梁的配筋率, 提高结构的峰值承载力及变形能力，正好与图中加固曲线峰值承载力高于截断曲线峰值承载力相吻合。并可以看出A2 模型用GFRP 布纵向加固后，梁悬链线阶段承载力明显提高，但在梁机制阶段的作用有限，这是由于GFRP 布虽然具有良好的受拉极限变形能力，但在前期梁受弯阶段不能很好的发挥出来，而在后期悬链线机制阶段可以充分发挥它的抗拉能力。

对于梁关键截面S2 处，A1 与A2 梁上部截面在整个受力过程一直承受拉应力，而A1 与A2 底部构件先受压应力后受拉应力，并分别在300 mm 与268 mm 达到应力拉压转换点后进入悬链线受拉阶段，即A2 先于A1 进入悬链线机制阶段，但转换点的位置与荷载-位移曲线中的位置不完全一致，这是由于梁受力机制中的转换点并不完全由钢筋决定，而是受钢筋混凝土与GFRP 布的共同影响。并可以观察到S2 截面无论上部测点还是下部测点构件破坏时，均没有超过规范规定的1/5 跨度（600 mm）的限制，S1 截面亦是。模拟中存在的误差在于：材料的非线性，弹塑性材料钢筋与GFRP 布和混凝土之间的粘结作用；实际结构中变形使得GFRP 布与梁之间有剥离现象等在OpenSees 有限元软件中无法考虑。

由上分析可知，由于前期受弯阶段GFRP 布不能发挥受拉性能，A2 加固模型拉应力主要靠钢筋承受，A1、A2 在此阶段具有较为接近的抗倒塌能力与竖向变形数值。后期随着变形的发展，梁全截面受拉使得梁的挠度越来越大，GFRP 布的抗拉性能也逐渐发挥。A2 模型承受拉应力的能力迅速提升使得结构先于A1 模型进入悬链线机制阶段，并且梁上部钢筋采用GFRP 加固的A2 模型悬链线机制承载力较A1 提高了16.45%（见表5）。

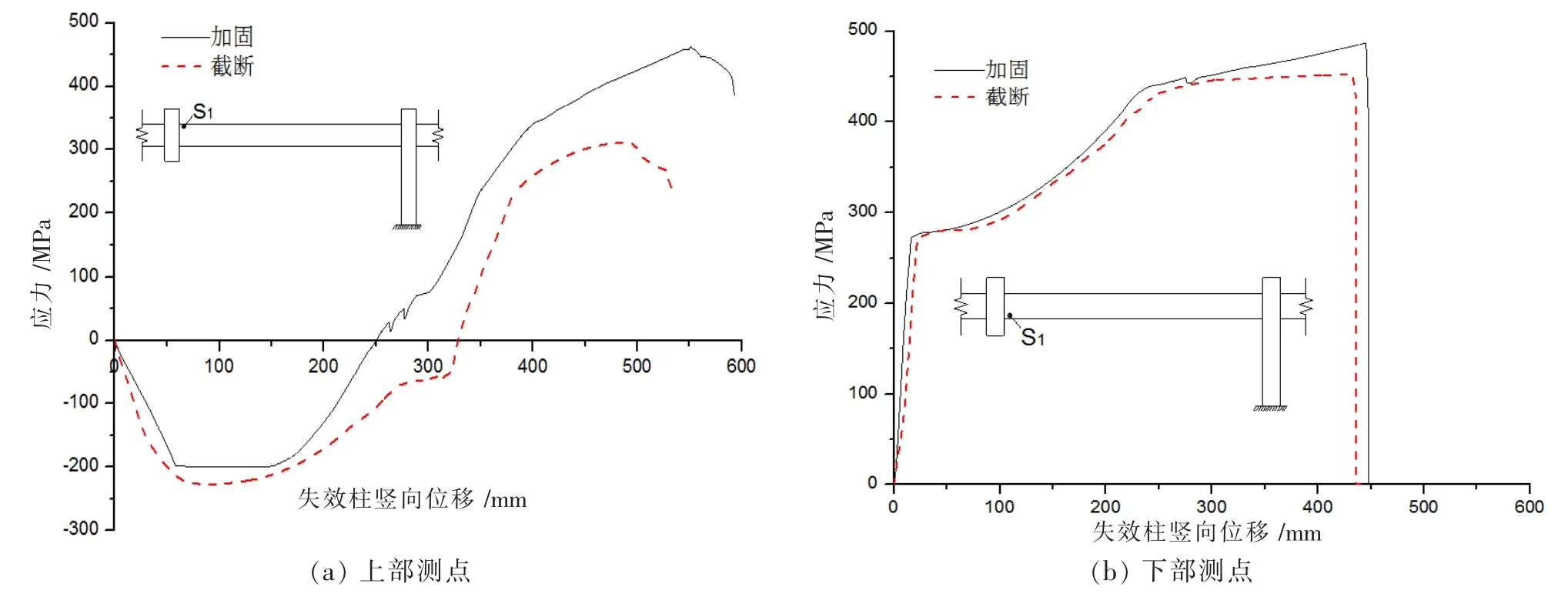
图11 梁关键截面S1 位移-应力图

图12 梁关键截面S2 位移-应力图

表5 承载力提高率

4 结论

采用OpenSees 进行数值模拟分析，比较了RC梁柱子结构在梁上部钢筋跨中按规范截断布置与截断基础上采用GFRP 布加固布置下的结构连续倒塌过程，得出以下结论：

（1）框架梁柱子结构在连续倒塌过程中，梁机制阶段的位移-荷载关系不受GFRP 布加固与否的影响，采用GFRP 加固可以使结构提前进入悬链线机制阶段；

（2）悬链线机制的存在可以使框架梁柱子结构最终承载力提高16.45%，采用GFRP 布加固提高最终承载力的效果要比按规范梁上部钢筋截断布置要好；

（3）由于塑性理论计算是简化的力学模型，因此与数值模拟中的本构关系存在一定差别，造成理论计算值比数值模拟值要小。