一次模拟联考中的文理科导数综合题命制过程

☉湖北省恩施州教育科学研究院 周 威

2019年3月湖北省七市州联考在紧张的复习备考中结束，笔者恰好与十堰程老师、宜昌向老师担任此次模拟考的命题任务，从湖北省教育学会2019年3月的质量分析会来看，颇为好评.现将此次联考文理科中两个导数压轴题的命制过程进行简单总结，与大家分享交流.

一、文科导数综合题的主要命题过程

1.从理科高考题中寻找文科命题的灵感

一直以来，联考或者模拟考的命题都是以高考为模板，改编策略的文章也比比皆是，事实上，高考题也确实是最好的原创命题素材.2018年全国理科数学卷Ⅱ的第21题导数综合题也一直被许多专家拿来深入研究或改编，原题如下：

题目已知函数f（x）=ex-ax2.

（1）若a=1，证明：当x≥0时，f（x）≥1；

（2）若f（x）在（0，+∞）内只有一个零点，求a.

这道题不是太难，但作为考查文科生一轮复习情况确实可以了，再加之现在文理合卷是必然，那么能不能从此理科题出发，命制一道此次联考的文科导数综合题呢？虽然改编较多，但是都保留了f（x）=ex-ax2本身不动.灵感一来，就继续思考：如何对f（x）本身进行改编成为一个全新的函数？第一感觉就是若把参数a提前作为ex的系数构成一个新的函数，那么第一问就可以令a等于某个常数，改编成常规的求单调区间问题；第二问自然通过某个不等式成立时，探究参数a的范围来考查学生的数学抽象、逻辑推理、数学运算的核心素养.这种结构也恰好与上面的高考题保持一致.

2.从积分计算中确定函数表达式

首先，如何确定f（x），是不是就简单地变为f（x）=aex-x2？但总感觉就是太“简单”，让人忘不了“原型”，于是构建了函数f（x）=aex-（x+1）2，但在第一问中求导之后，要确定f（x）=aex-（x+1）2的单调区间时，要二阶求导，这与文科历年高考有出入.那么如何解决这一个问题呢？最好的方法就是在求导之后能进行因式分解.要出现因式分解，就必须有（x+1）公因子，也就是aex部分要加入一个因式使得求导之后变为aex（x+1）的形式，那么其原函数是什么呢？于是通过不定积分axex+C，最终将函数修改为f（x）=axex-（x+1）2.表达式简洁干净，完全没有了“原型”的影子.

3.从数形结合中确定设问

根据之前的设想，令a=1得到了第一问：若a=1，求函数f（x）的单调区间.那么如何通过某个不等式成立时，探究参数a的范围呢？诚然，必须画出此函数的图像，为了方便快捷，通过几何画板动态演示a变化时图像的形状，如图1所示：

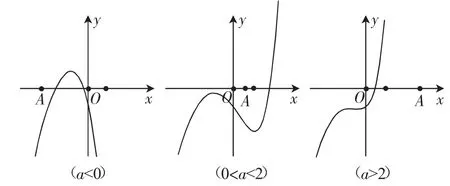
图1

图中A点的横坐标表示a的值，通过移动A点时的细心观察，在a为正数变化时，总在x≥1部分，有f（x）≥-2恒成立！到这里，不免让人有点激动，因为第二问就可以设为：若x≥1时f（x）≥-2恒成立，求a的取值范围.那么计算的角度能不能做出来答案呢？如是笔者着手计算，结果如预设一样，恰好可以！但考虑到高考中主要是以f（x）≥0恒成立为主，所以对原函数作了向上移动两个单位的修改，如是题目最终呈现为：

文科成题已知函数f（x）=axex-x2-2x+1（其中a∈R，e为自然对数的底数）.

（1）若a=1，求函数f（x）的单调区间；

（2）若x≥1时，f（x）≥0恒成立，求a的取值范围.

4.从“一题多解”中验证结果

第一问的解答，自然是考查学生基础知识，基本运算，基本方法，直接求导，根据固定步骤求出f′（x）的零点（解答略）.第二问主要考查学生的分类讨论，具体解答为：

解法1：（2）由已知得f′（x）=aex（x+1）-2（x+1）=（x+1）（aex-2）=0，其中x≥1.

①当a≤0时，由于x≥1，得f′（x）=（x+1）（aex-2）＜0，故f（x）在［1，+∞）上为减函数，显然不成立.

那么，此题是否陷入单一解法的思维定式呢，对于平时复习中经常用到的“分离变量”是否可以呢？简答如下：

解法2：x≥1时，f（x）=axex-x2-2x+1≥0恒成立，即对x≥1恒成立，令，则h′（x），所以

对h（x）求导看似复杂，实则计算完毕的时候恰好分子中不含ex，给计算带来了方便.

5.从“变式”中强化考点

第二问的设问，只是我们考查学生知识、技能、思想与方法的诸多形式中的一种，事实上，我们还可以根据平时高频考点，进行如下设问，达到触类旁通的效果：

变式1：若函数f（x）在（0，+∞）内只有一个零点，求a的取值范围.

变式2：若方程f（x）=-1有解，求a的取值范围.

变式3：对任意的x1，x2∈（0，2），总有|f（x1）-f（x2）|≤ae，求a的取值范围.

二、理科导数综合题的主要命题过程

1.从改编中把握稳中求变的命题规律

理科函数零点问题从2017年以来就是热点，函数考查形式采取“指+幂”或“对+幂”或“指+对”的形式，导数一般不难求，例如2018年全国卷Ⅰ理科21题中f（x）2015年山东卷理科21题中f（x）=ln（x+1）+a（x2-x），2011年辽宁卷理科21题中f（x）=-ax2+（2-a）x+lnx等，都是类似lnx和二次式Ax2+Bx+C的组合，那么是否可以出现lnx和三次式Ax3+Bx2+Cx+D的组合呢？这种“变化”让人很自然地想到.如是经过查找资料，惊喜地发现了与lnx的组合，就有了如下题目主干与第一问：

思考：y=f（x）+g（x）的零点个数与a的关系好不好计算呢？

2.体现“多考一点想，少考一点算”

为了设置第二问和解答上面的思考，如是借助了几何画板得到简图，如图2、图3、图4所示：

图2

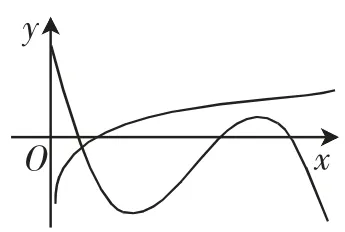
图3

图4

当a=-0.38时，y=f（x）+g（x）才有图2的情况，当a≥0时图像不是很理想，当a＜0时图像形状与图2差不多，只是位置不一样，也不好继续设问.但是，当分别画出f（x），g（x）的图像时，伴随a＜0变化，会出现图3和图4的情况，如果只考虑函数min{f（x），g（x）}的图像，那么函数min{f（x），g（x）}的零点会最多出现3个（图4）的情况，如是得到整个理科21题：

理科成题已知函数f（x）=lnx，g（x）=x3+2（1-a）x2-8x+8a+7.

（1）当a=0时，求y=f（x）+g（x）的单调区间；

（2）当a＜0时，记函数h（x）=min{f（x），g（x）}，x＞0，若函数y=h（x）至少有三个零点，求实数a的取值范围.

三、考试结果及反思

这两个导数综合题，都是在高考的影子中寻找出路，都是常规的求参数值或取值范围、求函数的性质（单调区间、最值、极值、零点等）、求解或证明不等式、处理探究性问题等知识点，考查学生的函数思想、转化与化归思想、数形结合能力、综合分析解决问题能力、运算推理能力等，预设难度是0.3至0.35.从笔者所在地区考试结果来看文科导数综合题的难度系数为0.18，理科导数综合题的难度系数为0.24，与其他地市交流时，这个难度系数值也差距不大.这就很好地达到了检查第一轮复习效果的目的，暴露了一轮复习中对导数综合应用的弱点，也为第二轮复习或专项复习提供了参考依据.

数学命题确实是一件让人痛苦并快乐的事情，它没有现成的套路，属于创造性的智力活动，在命题过程中，除了本文中说到的几点，也有很多文章关于这方面的真知灼见，总之，需要不断尝试、实验、探索、合作.值得一提的是，整个命题过程中都不可避免地用到了几何画板，它为我们在平时的试题改编、疑难求解提供了一种较为简便的途径，这也从另一个角度说明了信息技术2.0时代，数学课堂与数学软件的结合必然是大势所趋.