三角求值方法多,等价变换最关键
——2019年全国卷Ⅱ三角求值题
☉江苏省张家港市乐余高级中学 王庆龙
三角函数的求值问题一直是高考中三角函数问题的常见题型之一,而三角恒等变换是三角求值中的关键所在.由于三角函数公式繁多,关系又错综复杂,解题时既有多种公式可供选择,又容易陷入公式无从选择的困境.三角函数的求值问题在解法上具有多样性,解题切入口也不唯一,对运算能力要求比较高,是考查综合能力的良好载体,也是很好地考查学生思维的灵活性、多样性、拓展性的场所.
一、真题在线
【高考真题】(2019·全国卷Ⅱ理科·10;文科·11)已知,则sinα=( ).
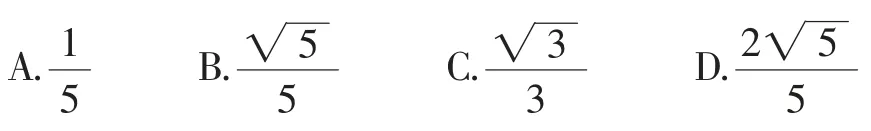
本题短小精悍,条件简单,难度中等,可利用的三角函数公式众多,切入点多样.根据题目中二倍角与单倍角的关系,可以借助三角恒等变换加以转化,当中可以利用同角三角函数基本关系式及相关的公式来处理;也可以借助三角函数定义,利用参数x,y,r的代数运算来处理;还也可以直接通过选项中的结果来进行验证处理,从而达到求解目的.
二、一题多解
破解视角1.三角恒等变换法
解法1:(平方关系转化法1)由题中关系式2sin2α=cos2α+1,可得cos2α=2sin2α-1.
利用二倍角公式可得cos2α=2cos2α-1,则有2sin2α-1=2cos2α-1,即sin2α=cos2α.
而sin2α=2sinαcosα=cos2α,结合,可得2sinα=cosα.
将cosα=2sinα代入平方关系sin2α+cos2α=1,可得
故选择答案:B.
解法2:(平方关系转化法2)由题中关系式2sin2α=cos2α+1,可得
代入平方关系sin22α+cos22α=1,可得cos22α=1,整理可得5cos22α+2cos2α-3=0,解得或cos2α=-1.
故选择答案:B.
点评:利用平方关系或平方运算、万能公式等方法来处理,结合同角三角函数基本关系式与二倍角公式的转化与应用,都充分体现了方程思想及三角恒等变换思维.这也是解决此类问题的常见思维,通技通法.
破解视角2.三角函数定义法
解法3:(三角函数定义法)由于,在角α的终边上取一定点P(x,y)(x>0,y>0)
由题中关系式2sin2α=cos2α+1,可得4sinαcosα=2cos2α,即2sinαcosα=cos2α.
故选择答案:B.
点评:通过三角函数的定义的导引,把相应的三角函数值问题转化为相应的定义中有关参数x,y,r的关系式,利用关于x,y,r的代数运算,并结合方程的思想来处理与转化,进而求解相应的三角函数值.这是解决此类问题的特殊思维,回归定义.
破解视角3.验证法
解法4:(代入验证法)已知
故选择答案:B.
点评:验证思维是破解选择题比较常见的一类思维方式,借助各对应选项中的结果,逆向思维,将对应的结果代入题目条件,逆向运算,产生与条件或已知结论矛盾的情况就是错误的选项.验证法有时也是破解问题的一大“杀技”.
三、变式探究
探究:保持原题条件,改变所要求解的三角函数名称,从最简单的层面加以变形与拓展,难度相当.
【变式1】已知,则cosα=( ).

解析:由题中关系式2sin2α=cos2α+1,可得cos2α=2sin2α-1.
利用二倍角公式可得cos2α=2cos2α-1,则有2sin2α-1=2cos2α-1,即sin2α=cos2α.
而sin2α=2sinαcosα=cos2α,结合,可得2sinα=cosα.
故选择答案:D.
【变式2】已知,2sin2α=cos2α+1,则tanα=( ).

解析:由题中关系式2sin2α=cos2α+1,可得cos2α=2sin2α-1.
利用二倍角公式可得cos2α=2cos2α-1,则有2sin2α-1=2cos2α-1,即sin2α=cos2α.
而sin2α=2sinαcosα=cos2α,结合,可得2sinα=cosα,所以
故选择答案:B.
四、解后反思
充分挖掘课本知识,拉近课本与高考之间的距离,架起两者之间对应的桥梁,是平时数学教学与学习的一个关键所在.进而有意识地针对一些典型高考真题,就某一层面的知识体系加以一题多解、一题多变剖析,从课本基本知识与基本方法入手,从多个角度切入,到多个思维破解,真正达到横看成岭侧成峰,远近高低各不同.

