西藏旅游收入预测模型的对比分析

陶 青

（西藏民族大学财经学院 陕西咸阳 712082）

一、引 言

西藏有着悠久的历史文化资源和优异的自然资源禀赋，在全世界是独一无二的，是世界十大旅游目的地之一。西藏旅游业也在西藏经济发展中扮演着越来越重要的角色。旅游对经济的贡献也成为西藏制定经济发展政策的重要因素，尤其在中央第五次西藏工作座谈会确立把西藏建设成为“中华民族特色文化保护地和重要的世界旅游目的地”的战略定位以来，西藏对旅游业发展提出了更高要求。因此，开展旅游收入预测研究，有利于我们定量认识旅游业发展水平，为政府决策提供参考，促进西藏经济更好更快地发展。

二、数据收集与处理

本文以1981-2016年西藏旅游收入数据为研究对象。数据均来自于《西藏统计年鉴2017》，以下所建模型的训练集均为1981-2014年数据，测试集为2015-2016两年数据（见表1）。

为了初步判断西藏旅游收入序列特征和趋势性，作出序列图（如图1所示）。从图中可以看出，西藏旅游收入存在明显上升趋势，除2008年较2007年有明显下降外，其余年份均环比增长，且增速不断扩大。

三、模型选择与估计

（一）指数曲线模型

根据时序图趋势判断，西藏旅游收入数据类似一条指数曲线，因此将1981-2014年数据作为测试集试建立指数曲线模型:

其中，yt为西藏旅游收入取值，t为年份，a、b为待估参数，e为自然对数。为估计模型，首先对（1）式两边取对数，变换为:

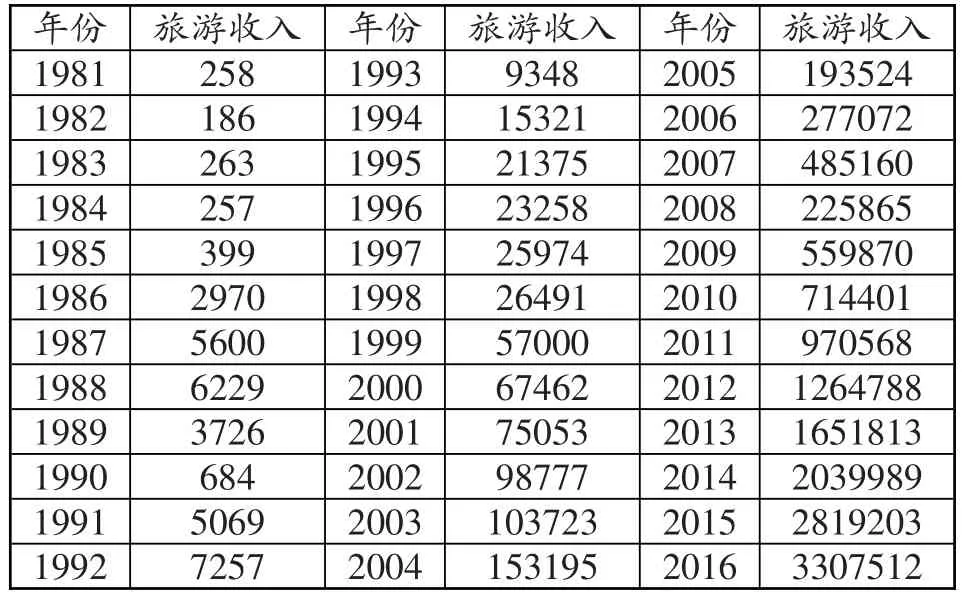
表1:1981-2016年西藏旅游收入数据（单位:万元）

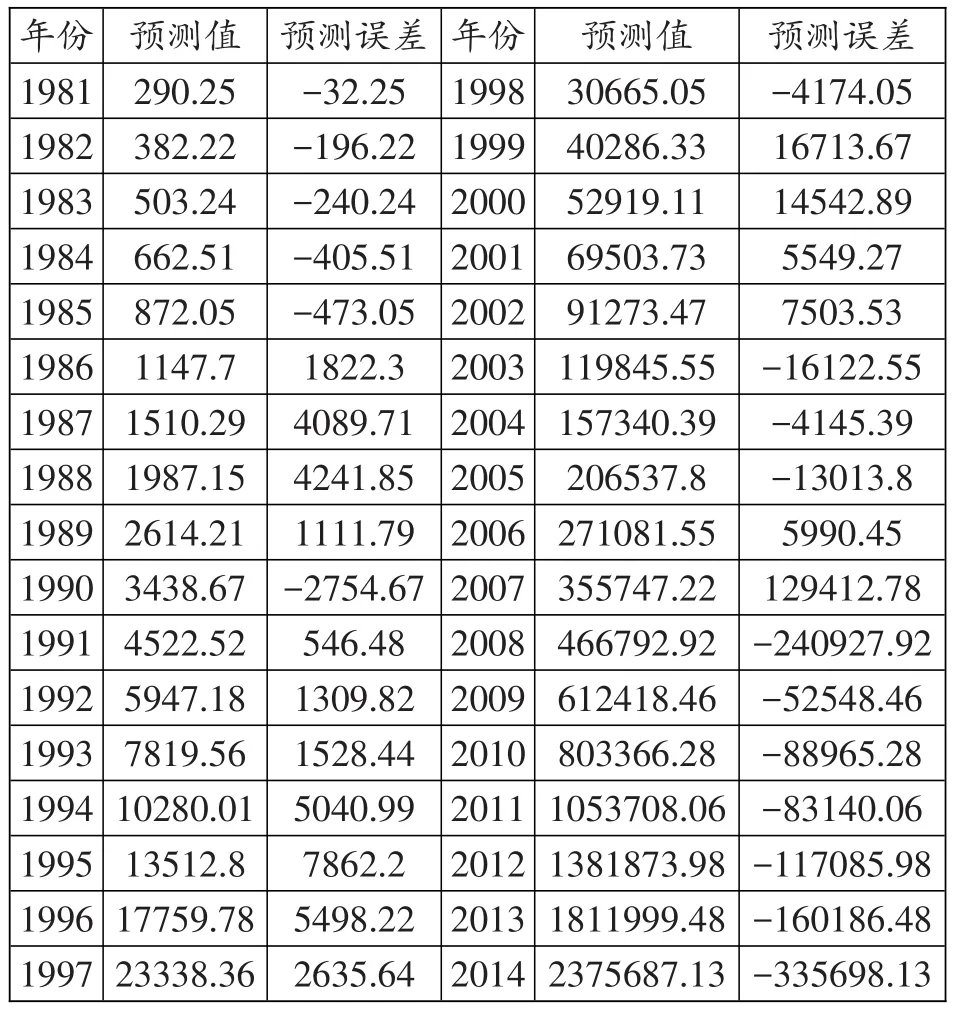
表2:指数曲线模型的拟合值及拟合误差（单位:万元）

根据模型得到的预测曲线及预测区间如图2所示，由于西藏旅游收入数据的量级发生了很大改变，导致从图形上看，曲线拟合状况尚可，但平均绝对百分比误差（MAPE）较大，为46.39%。

图1:西藏旅游收入1981-2016年时序图

图2:曲线模型拟合线及估计区间

（二）光滑样条法

指数曲线回归是非局部回归，是在整个数据集上进行拟合，单个观测值会对整条曲线拟合产生影响。由于西藏旅游收入数据变化较大，这种非局部回归模型效果不甚理想。一种可行的改进方法是将数据分成多个连续区间，在每个区间上用单独模型拟合，即回归样条法。

1、光滑样条法简介

首先根据定义域[a,b]内的观测点t1……tn将其分成多个区间，（a＜t1＜t2＜……＜tn＜b），模型g(t)采用分段的三次多项式

其中定义t0=a,tn+1=b,i=0,1,2……n

然后求解最优的g(t)。最优模型应该同时满足以下两个条件:（1）估计误差尽可能小；（2）曲线尽可能光滑，曲线越光滑，模型泛化能力越强。衡量曲线光滑性有多种办法，比如拐点个数，二阶导数值等，此处采用二阶导数积分（∫(g'')2dt），二阶导数对应的是斜率变化程度，其积分（∫(g'')2dt）则代表了g'(t)在整个取值区域内整体的变化情况。曲线越光滑，其取值越小。综上，使式（4）最小的g(t)为最佳估计。

2、λ的选取

上述模型中采用“误差+惩罚项”形式选择模型，λ∫(g'')2dt是对模型g(t)波动性惩罚，λ衡量惩罚项所起作用大小。λ=0时，惩罚项不起作用，模型结果波动性会很大，当λ=∝时，模型结果很稳定，趋于一条直线。我们通过交叉验证法，选出使得误差RSS尽可能小的λ。交叉验证误差为

3、模型结果

和指数曲线模型类似，采用1981-2014年西藏旅游收入数据作为训练集拟合模型，2015-2016两年数据作为验证集计算模型准确率。图3是应用光滑样条拟合结果，虚线是应用交叉验证法选择λ后得到光滑样条，实线是自主选择λ得到结果。图中可以明显得看出，交叉验证法拟合得更佳，表3给出了训练集内拟合值以及拟合误差。

图3:光滑样条法估计结果

表3:光滑样条法的拟合值及拟合误差

（三）ARIMA模型

1、序列的平稳化处理

从图1可以看出西藏旅游收入的序列存在显著上升趋势，属于非平稳时间序列。根据序列特点，采用差分方式提取数据所蕴含的确定性信息。从时序图4可以清楚看出，一阶差分只提取原始序列中部分信息，其仍蕴含着向上趋势。因此对差分后序列再做一次差分运算，得到二阶差分序列。二阶差分序列确定性趋势基本消除。

图4:一阶差分与二阶差分序列图

为判断二阶差分序列是否为平稳性序列，对其进行ADF单位根检验，计算得到其ADF统计量的值为-3.5378对应的PT值为0.05，即在5%显著性水平下，二阶差分序列平稳。

2、ARIMA（p,d,q）模型估计和检验

由序列平稳化过程可知，d=2。为确定p、q取值，画出二阶差分序列自相关系数和偏自相关系数图，如图5所示，该序列自相关系数一阶截尾，偏自相关系数2阶截尾，初步确认滞后阶数为:p=2，q=1。

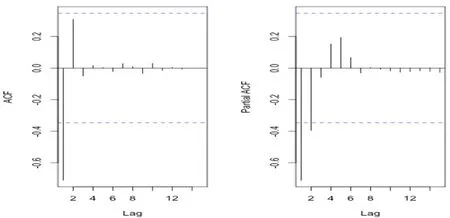
图5:二阶差分序列的自相关与偏相关系数图

为进一步确认自回归阶数p和移动平均阶数q取值，现计算不同p和q（最大p和q均设置为5）取值下相应BIC值，其结果如图6所示，

图6:对于不同的p和q计算相应的BIC值

从图6可以看出，自回归滞后一阶，移动平均滞后1阶或者三阶，BIC值均较小。试分别做ARIMA（1,2,1）和ARIMA（1,2,3）模型，估计结果如表4和表5所示，可明显看出，ARIMA（1，2，3）模型系数的标准误差较大，系数基本不显著，因此该模型属于过渡拟合模型。ARIMA（1，2，1）模型系数均显著，AIC的值相比ARIMA（1，2，3）模型略小，因此，最终模型考虑选择ARIMA（1，2，1）。

表4:ARIMA（1，2，3）模型的回归结果

表5:ARIMA（1，2，1）模型的回归结果

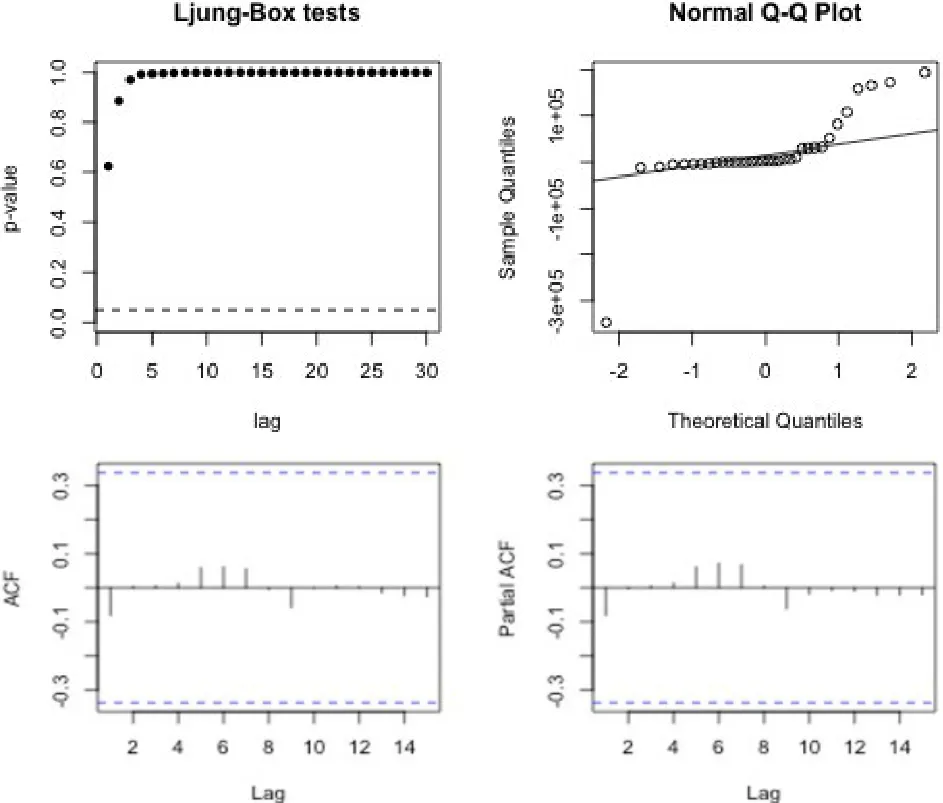
图7:残差诊断图

表6:ARIMA模型拟合值及拟合误差

模型检验是为了检验残差是否为白噪声，诊断图如图8所示。Ljung-Box的原假设是序列独立（和某阶滞后相比），p值很小说明存在相关性，对于不相关的序列，p值很大。Ljung-Box检验（诊断图左上）的p值均在0.6以上。从Ljung-Box检验、acf和pacf图可以看出，这个模型的残差是一个随机过程。从Q-Q图（诊断图右上）来看，散点基本在一条直线附近，说明模型的残差分布近似正态。综上，基本可以断定模型的残差序列是白噪声序列。

3、拟合值与拟合误差

根据1981-2014年数据建立的ARIMA(1,2,1)模型，计算拟合值和拟合误差如表6所示。

四、模型对比与预测

现将三个模型应用于测试集，即用西藏2015-2016年两年旅游收入数据对模型进行测试，判断模型应用效果。计算每个模型平均绝对百分比误差

表7:三个模型的平均绝对百分比误差

由表7可知，从测试集预测误差来看，光滑样条法优于ARIMA模型，优于指数模型。指数模型和ARIMA模型训练集平均绝对百分比误差均在45%左右，测试集在15%左右，这两个模型都是以模拟所有数据，从中找到经济活动变化规律为主要技术手段。西藏旅游收入这一经济变量，在1990和2008年出现大幅度下滑，环比下降81%和53%。在1986年和1999年急速上涨，环比增长664%和115%。对于这种缺乏明显模式的数据，这两个模型捕捉到的信息量有限。光滑样条法通过采用分段拟合方式克服这种缺点，提取信息量更大，测试集的平均绝对百分比误差只有10.9%。光滑样条法所需要的假定要比ARIMA模型和指数模型弱得多，尤其没有假设变量的函数形式（指数曲线模型假设数据来自于指数分布），使其对西藏旅游收入这一数据的拟合更有效。另一方面，西藏是一个边疆民族地区，由于其民族、宗教问题的特殊性，西藏地区的稳定问题是重中之重。旅游产业发展，除了市场的因素外，政策因素影响也不可忽略，在建模过程中，政策影响很难量化，这也是指数模型和ARIMA模型拟合结果不理想的原因。

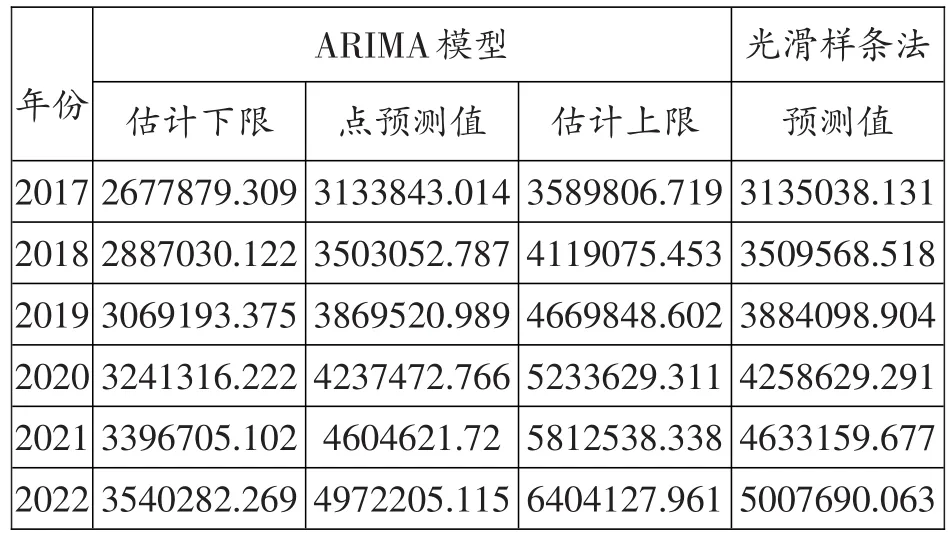
表8:ARIMA模型和光滑样条法的估计结果

虽然指数模型和ARIMA模型的预测精度不如光滑样条法高，但指数模型和ARIMA模型可以估计预测区间，而光滑样条法只能做点值预测。因此，为了更全面预测未来5年西藏旅游收入，建议采用ARIMA模型和光滑样条法对西藏2017-2022年西藏旅游收入进行预测，结果如表8所示:给出了95%置信水平下旅游收入的预测区间，和光滑样条法的预测值。