基于量子遗传算法的FARIMA模型电力负荷短期预测*
杨照坤, 宋万清, 曹 琨
(上海工程技术大学 电子电气工程学院,上海 201600)
0 引 言
负荷预测的质量是保障用户侧用电的一个重要因素[1]。因此精确的短期负载预测,可以为电力调度和规划提供可靠的参考依据,在一定程度能避免欠负荷跳闸危机以及过负荷的能源浪费等问题。能够让调度人员及时或者提早的对各地区的电网的超负荷或欠负荷做出调节,以免造成由于电网波动对二次侧的用电用户造成不必要的损失。许多学者对电力负荷预测进行了大量的研究,如指数平滑[2]、大数据[3~5]等方法都相继被用到短期负荷预测模型中。然而,由于负荷预测具有模糊性和非线性的特点,导致上述方法的预测精度不高,而且神经网络[6;7]、模糊多目标遗传优化算法[8;9]等只考虑单一的影响因素,所以效果不明显。FAIMA算法具有对长相关序列很好的预测功能,且模型训练所需参数较少,较少出现过拟合问题,对异常值的鲁棒性好[10],但在对FARIMA模型进行定阶时,Hurst指数定阶准则却不一定是最优解。
本文由量子遗传算法优化FARIMA模型,量子遗传算法根据合适的适应度值进行全局搜索,确定模型的最佳阶数[11],使得该算法在提高短期电力负荷预测精度和误差收敛速度方面具有一定的优势。
1 FARIMA模型
FARIMA一般记为FARIMA(p,d,q)。其中,d为分数差分阶数,p为自回归项阶数,q为滑动平均阶数
Φ(z-1)(1-z-1)dxt=Θ(z-1)εt
(1)
式中 {xt:t=…,-1,0,1,…}为时间序列,d∈(-0.5,0.5),{εt:t=…,-1,0,1,…}为一零均值方差为σ2的白噪声序列。Φ(z-1)和Θ(z-1)分别为p阶自回归(auto regression,AR)多项式和q阶滑动平均(moving average,MA)多项式
Φ(z-1)=1-φ1z-1-φ2z-2-…-φpz-p,
Θ(z-1)=1-θ1z-1-θ2z-2-…-θqz-q
(2)
式中 Δ=(1-z-1)为差分算子,则Δd为分数差分算子,其二项展开式为
(3)

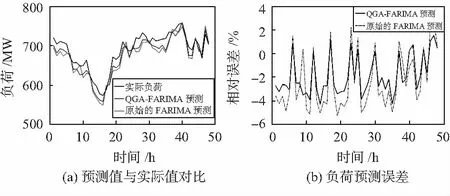
序列的自相似性可以用Hurst指数来度量。Hurst指数的取值范围为0.5 量子遗传算法(quantum genetic algorithm,QGA)是量子计算与遗传算法相结合的产物,它建立在量子的态矢量表示基础之上,将量子比特概率幅表示应用于染色体编码,使得一条染色体可以表达多个态的叠加,并利用量子旋转门实现染色体的更新操作,从而实现了对目标函数的优化求解。其主要操作为量子比特编码和量子门更新。 1)量子比特编码 QGA 不是采用传统遗传算法的二进制、浮点数、符号等染色体编码方法,而是采用一种新颖的量子位染色体表示法。用量子比特来表示一个基因,具有能同时表达任意叠加态的特点。采用量子比特编码的染色体结构可表示为 (4) 式中qj为第j个个体的染色体;k为编码的每个基因的量子比特数;m为染色体基因个数;α和β分别为|0〉和|1〉的概率幅,且满足归一化条件 |α|2+|β|2=1 (5) 式中 |α|2为量子测量值为0的概率;|β|2为量子测量值为1的概率。 2)量子门更新 量子门作为演化操作的执行机构,可根据具体问题进行选择,根据量子遗传算法的计算特点,选择量子旋转门较为合适。量子旋转门调整操作为 (6) FARIMA模型通过差分后即ARMA模型,通过量子遗传算法来优化ARMA模型的阶数。对模型的阶数(p,q)进行优化,在所有的解空间内,根据合适的适应度值进行全局的搜索,从而能够确定模型的最佳阶数(p,q),FARMA(p,d,q)模型的建模过程可分解为“分数差分”和“ARMA预测”两部分过程。 分数差分过程的关键是获取参数d。首先通过Hurst参数估计法得到H的值,再由d=h.0.5得到d的估计值。通过对时间序列的分数差分滤波处理即可得到一个ARMA过程。运用AIC信息准则对ARMA模型进行定阶。 AIC信息准则定义如下 (7) 将寻找AIC最小值作为量子遗传算法的适应度函数。由量子遗传算法算法得到较优的AIC(p,q)值,其寻优过程为: step1:初始化父代染色体 step2:对每个染色体基因位即量子位进行测量,得到一个状态。对每个状态计算适应度,记录最佳个体及适应度。 step3:遗传进化设定的代数,其中采用量子旋转门对每一代染色体进行遗传变异 step4:达到终止条件,输出最佳个体及适应度。 本文利用量子遗传算法优化的FARIMA模型来对短期电力负荷进行预测,算法流程如图1所示。 图1 短期电力负荷预测流程 选取上海电力公司采集到的17 520个连续时间点(每隔30 min采集一个点)的电力负荷值作为样本容量,然后随机取中间连续的5天工作日240个点作为预测样本,以前4天工作日192个点作为训练数据,第5天48个点作为测试数据。采用横向对比法和纵向对比法对异常数据进行修正,再对输入数据进行归一化处理,最后在输出层对数据进行反归一化处理。 在MATLAB环境下,分别用原始的FARIMA模型和基于量子遗传算法优化的FARIMA模型对数据样本进行训练和预测,并与实际负荷值进行比较,仿真结果如图2(a),原始的FARIMA模型和基于量子遗传算法优化的FARIMA模型预测误差对比如图2(b)所示。原始的FARIMA模型和基于量子遗传算法优化的FARIMA模型预测的精度、平均相对误差、最大相对误差如表1所示。 图2 改进前后FARIMA模型仿真结果 表1 改进前后FARIMA模型误差数据对比 由图2(a)可看出:原始的FARIMA模型和基于量子遗传算法优化的FARIMA模型的曲线走势都比较接近实际值的曲线走势。通过图2(b)和表1可看出与基于量子遗传算法优化的FARIMA模型相比原始的FARIMA模型预测输出值与实际值之间出现较大的偏差,而基于量子遗传算法优化的FARIMA模型的预测输出值则更接近实际值。可见使用量子遗传算法大大减小了算法的计算时间,而且提高了预测精度。 本文采用自适应函数法将可靠性约束引入目标函数构建了自适应适应度函数,结合自适应旋转角调整策略、量子位交叉变异操作,提出了一种基于量子遗传算法优化的FARIMA模型,用于求解该复杂非线性规划问题,经过与原数据、原始的FARIMA模型和基于量子遗传算法优化的FARIMA模型对比结果表明,该算法具有收敛速度快、全局寻优能力强等优点。2 量子遗传算法
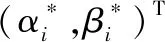
3 量子遗传算法优化的FARIMA模型
4 短期电力负荷预测

5 仿真实验

6 结 论

