基于Volterra级数扩展模型的变步长VFxBSLMS算法*

仝喜峰, 陈卫松, 钱隆彦

(安徽师范大学 物理与电子信息学院,安徽 芜湖 241000)

0 引 言

由于脉冲噪声的冲击特性,自适应算法在脉冲噪声环境下的鲁棒性尤为重要[1,2]。脉冲噪声不符合高斯分布特性,信号在时域上分布着大量的尖峰脉冲(冲击信号),其统计特性就表现为较厚的概率密度函数拖尾。针对脉冲噪声,通常利用标准对称稳态分布来建模[2],只有阶数小于α的分数低阶矩是有限的(α为特征指数,直接决定α稳态分布的概率密度函数拖尾厚度),由于不存在有界的二阶矩,线性控制算法在脉冲噪声控制中的性能显著降低,一些非线性的滤波算法受到关注。

另一方面,由于设备的非线性特性及次级通道的非线性失真现象的存在,线性控制算法表现不佳,甚至无法收敛。为了提高线性控制算法在非线性噪声控制中的性能,Tan L和Jiang J提出了基于Volterra级数的非线性VFxLMS算法[3,4],相比于线性FxLMS算法,VFxLMS算法可以解决算法无法收敛的问题,但降噪效果不够好。为了保证非线性控制算法的稳定性,Leahy R等人发现脉冲噪声存在有限的分数低阶矩,提出的FxLMP算法被用于脉冲噪声控制,具有较好的收敛效果,不足之处在于需要脉冲噪声的先验知识[5]。Wu L等人指出α稳态分布的脉冲噪声的对数阶矩是有限的,脉冲噪声经过对数变换后接近于高斯分布,提出了一种基于对数变换FxlogLMS算法,该算法对脉冲噪声更具鲁棒性,并且不需要噪声的先验知识[6]；但该方法存在权重更新死区的缺点,因此实用性较低。最近,Lu L等人提出了一种基于Volterra扩展模型(VFxlogLMP)的非线性自适应算法[7]，VFxlogLMP算法可以有效地解决FxlogLMS算法的滤波器更新死区弊端,并可以取得更好的收敛速度和降噪效果,但算法仍然需要噪声信号的先验知识,并且该算法计算量相对较大。

本文采用一种S型非线性函数对误差信号进行预处理,从而达到控制冲击信号的目的,确保算法的稳定性,在此基础上将变步长算法思想引入到非线性滤波算法中。仿真分析结果表明,该算法在不需要噪声先验知识的情况下,实现对脉冲噪声的控制,且不存在滤波器权值更新死区。

1 自适应Volterra滤波理论基础

Volterra滤波器可以很好地模拟非线性系统,对于各种高阶内核或脉冲响应,其输出仍然为线性。通过使用Volterra级数扩展,自适应非线性控制器的输出y(n)表示为

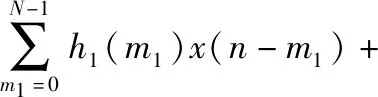
(1)

式中N为自适应Volterra滤波器的存储长度,hr(m1,…,mr),r=1,…,R为滤波器的第r阶核,这里选用二阶Volterra非线性滤波器,其输入信号可表示为

X(n)=[x(n),x(n-1),…,x(n-N+1),

x2(n),…,x2(n-N+1)]T

(2)

滤波器的权重矢量为

W(n)=[h1(n),…,h1(N-1),h2(0,0),…,

h2(N-1,N-1)]T

=[w1(n),w2(n),…,wN-1(n)]T

(3)

式中d(n)为期望信号,滤波器的输出和误差信号分别为

y(n)=XT(n)W(n),e(n)=d(n)-y(n)

(4)

Wu基于α稳冲噪声的对数阶矩有限,提出了FxlogLMS算法,滤波器的系数更新规则为[6]

(5)

为了克服FxlogLMS算法存在滤波器更新死区的弊端,Lu提出了基于Volterra级数的VFxlogLMP算法。修改之后的滤波器系数更新方程[7]

(6)

2 一种改进的Volterra自适应滤波方法

FxlogLMS算法和VFxlogLMP算法分别依据脉冲信号具有有限分数低阶矩和对数阶矩,控制了较大幅值的误差信号对自适应滤波器权值更新的影响。上述两种算法均可以用一般表达式表示为

W(n+1)=W(n)-μg(n)x′(n)

(7)

式中g(n)为与误差信号e(n)相关的权值更新函数。

S型激活函数是一个非线性连续函数,函数曲线形如“S”,其中S型激活函数的表达式为

(8)

式中S(x)为一单调奇对称的有界函数,本文将S型激活函数的单调有界特性引入到脉冲噪声控制算法中,定义代价函数为

(9)

因此,VFxBSLMS算法的权重矢量的更新表达式为

(10)

式中μ为步长因子,β为非线性压缩系数,且μ>0,β>0图1为不同β值下的非线性压缩函数曲线,从图中可以看出随着e(n)增大,g(n)值逐渐减小,这保障了在较大幅值e(n)下算法的稳定。β越大,g(n)对误差信号的压缩越剧烈。但β值选取并不是越大越好,对e(n)的过度压缩有可能会降低算法的收敛速度。

二阶Volterra滤波器的线性部分权值及二次项部分权值分别用wi(n)和wi,j(n)表示。Volterra滤波器非线性项将稳定分布的尖峰特性放大,导致输入信号的自相关矩阵特征值扩展变大,使输入信号相关性很强。为克服输入信号的强相关性以及固定步长对算法收敛带来的影响,本文采用基于Sigmoid函数[9]的变步长算法,其变步长公式为

μ1=μ2=σ[1/(1+exp(-λ|e(n)|))-0.5]

(11)

式中μ1(n),μ2(n)为基于Sigmoid函数的线性项和二次项的变步长因子。

考虑到误差信号中仍然存在大量的冲击信号,为了进一步地降低强脉冲信号对滤波器权值更新稳定性的影响,本文增加误差信号预处理环节。考虑到算法的适用性,在预处理函数的设置上体现出“动态”变化的特性。定义信号预处理函数表达式为

(12)

式中c(i)为误差信号的在线统计平均,i为信号样本数。

3 算法仿真与性能分析

以图2所示的FIR系统辨识模型为例,对本文算法进行仿真和性能分析[10]。

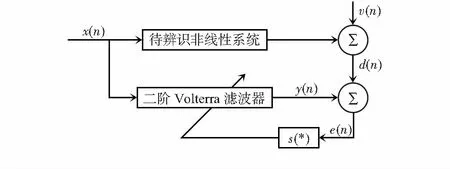
图2 系统辨识原理框图

设非线性系统是一个记忆长度N=3的二阶Volterra滤波系统,二阶非线性系统的期望信号为

d(n)=-0.76x-x1+x2+0.5x2+2·x·x2-

(13)

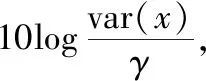
由于脉冲噪声的二阶矩不存在,因此利用平均残余误差ANR(Averaged Noise Reduction)来进行性能比较[11],其定义为

(14)

选取FxlogLMS、VFxlogLMP算进行比较,每种算法的最优步长通过实验的方式进行确定。图3为三种算法在脉冲噪声强度分别为α=1.2(图3(a)),α=1.5(图3(b)),α=1.8(图3(c))的环境下的降噪性能比较。

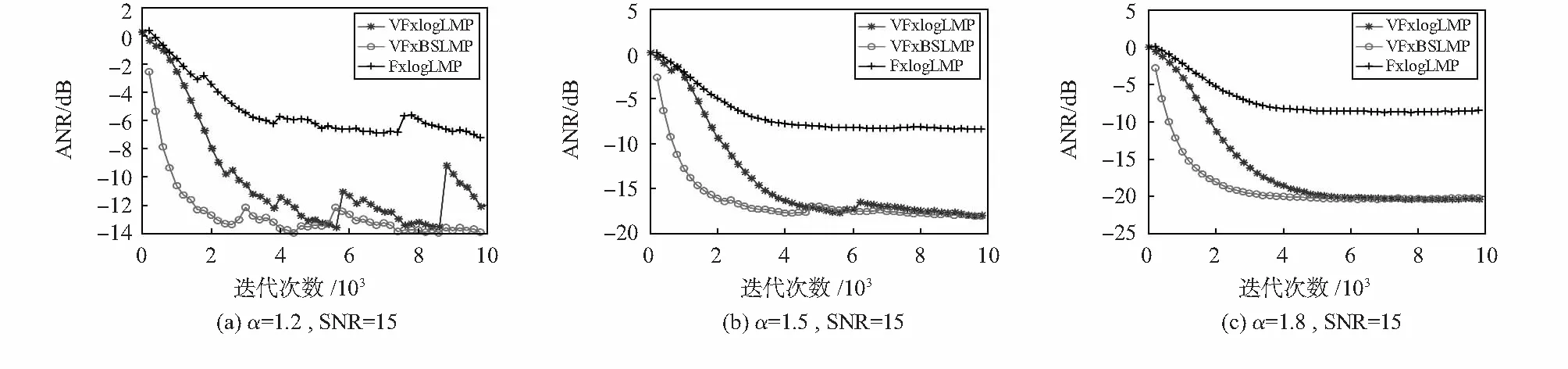
图3 三种算法的平均残余误差ANR对比

从图3(a)可见,当α=1.2(较强脉冲噪声背景)时,FxlogLMS算法相比较其他两种算法,平均残余误差的绝对值要小5～8 dB；VFxlogLMP算法和VFxBSLMS算法都可以取得比较理想的降噪效果,但VFxBSLMS算法在迭代2 500次左右就已经达到了收敛状态,而VFxlogLMP算法则要到4 800次才能完成,前者收敛速度明显较优。由于脉冲强度太大,三种算法在迭代过程中都不同程度上受到较高脉冲样本的干扰。由图3(b)和图3(c)可见,当α=1.5及α=1.8(脉冲强度较弱)时,三种算法对较弱的脉冲噪声环境都可以表现很好的鲁棒性。从不同噪声环境下三种算法的表现上来看,VFxBSLMS算法在算法收敛速度以及降噪效果上均优于FxlogLMS算法,在降噪效果上VFxBSLMS算法和VFxlogLMP算法都可以达到最高20 dB的降噪量,但收敛速度上VFxBSLMS算法仍然优于VFxlogLMP算法。

使用权系数误差范数对算法性能进行进一步的分析,所有仿真曲线都是通过20次独立仿真结果取平均得到

(15)

图4(a)是VFxlogLMP和VFxBSLMS算法在α=1.2时的权系数误差范数对比图,两种算法的误差曲线均可收敛到-20 dB,但在收敛速度上本文算法要远快于VFxlogLMP算法。

由图4(b)可以看出VFxBSLMS算法线性核误差(h1)及非线性核误差(h2)几乎同时在迭代450次左右达到收敛,而VFxlogLMP算法的线性核非线性核误差则要到1 600次才能达到收敛状态。两种算法的线性核误差值均小于二阶项核误差值,这是因为Volterra级数二阶项相关矩阵的特征值大于线性项。由于在图3(a),(c)已经表明FxlogLMS算法在收敛效果上低于VFxBSLMS及VFxlogLMP算法,本文不再对其进行权系数误差范数以及Volterra滤波器核误差的对比分析。

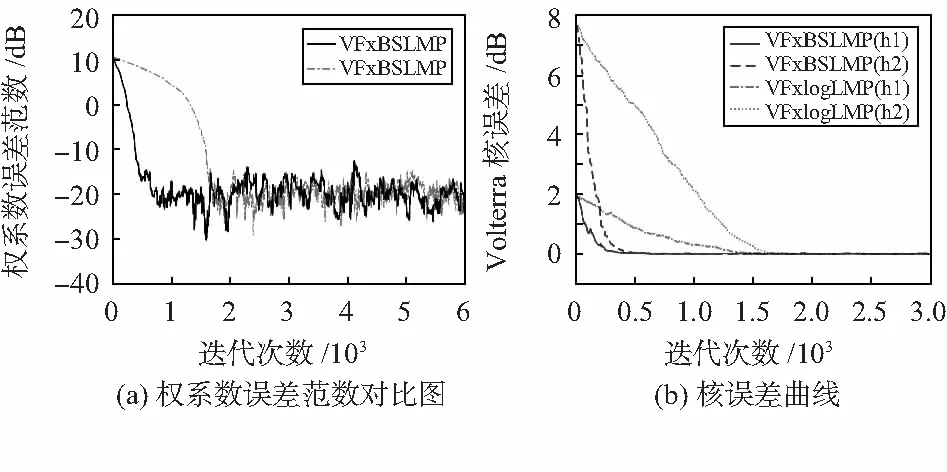
图4 α=1.2时算法性能比较

从图5(a)可以看出,当脉冲噪声强度较大(α=1.5)时,在迭代500次后,VFxBSLMS算法的噪声幅值稳定在6 dB以内,当迭代超过1 500次后稳定在2 dB内。而其他两种算法则在3～20 dB之间。当脉冲强度较小(α=1.8)时,在噪声衰减量上,VFxBSLMS算法的优势已经并不够明显,其主要原因是α=1.8时的噪声已经接近于高斯分布。在收敛速度上,本文算法噪声在迭代500次左右便呈现滤波完成状态,而其他两种算法则分别需要迭代1 300次和2 000次才能完成脉冲噪声滤波。

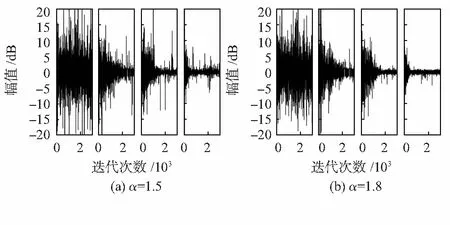
图5 不同算法的滤波效果对比

(从左至右分别为噪声信号、FxlogLMS算法、VFxlogLMP算法、VFxBSLMS算法)

4 结 论

仿真实验表明:本文算法构成的Volterra滤波器可以获得较快的收敛速度,并且不需要噪声信号的先验知识,适用环境较为灵活。由于本文引入变步长算法思想来进行步长更新,虽然提高了算法的收敛速度,一定程度上提高了算法的计算量负载,在进一步的研究中仍需不断改进,进一步减小计算量。