空射近空间飞行器助推弹道规划方法

杨 明,刘 明,郑 伟,高 兴,陈志刚

(1.国防科技大学 空天科学学院,湖南 长沙 410073;2.空间物理重点实验室,北京 100076)

空射模式是指由飞机载至空中发射,与地面发射相比较,其发射准备时间短、机动性强、发射成本低。一般空中发射动力系统多采用固体发动机。固体发动机燃烧时间短,要达到要求高度,火箭需采用多级工作模式,一般采用二级或三级,并且级间会增加无动力滑行以满足终端约束条件。美国轨道科学公司研制的飞马座空射火箭就是典型的空射火箭,并已进行多次飞行。它是三级固体火箭,由飞机载至空中,水平投放后,火箭按预定飞行程序将载荷运送到预定轨道,飞马座的成功为运载火箭发射开辟了新的途径[1-5]。

近空间飞行器一般在临近空间飞行,临近空间一般指距地面20～100 km区域。在临近空间区域飞行,既可以避免目前绝大多数的地面攻击,又可以提高军事侦察和对地攻击的精度,对于情报收集、侦察监视、通信保障以及对空对地作战等,具有极大的发展潜力[6]。

相对于传统地面发射或空射高轨道飞行器,空射近空间飞行器助推段弹道具有以下特点:①空射模式下,火箭投放后,一级飞行段需大过载快速拉起;②为了满足近空间飞行器低交班高度、小交班速度倾角和速度偏角的需求,助推段需采用特殊低弹道的飞行方案;③为实现近空间飞行器不同飞行距离要求,需在助推段进行能量管理,以满足不同的交班速度需求。这些特点都使得空射近空间飞行器助推段弹道规划问题变得更加复杂。文献[7]针对有翼空射运载火箭提出了一种基于飞行程序角的工程设计方法,文献[8]提出了一种基于自适应遗传算法的空射运载火箭弹道优化方法,文献[9]提出了一种基于攻角编码的遗传算法的高超声速飞行试验助推段弹道优化。以上研究主要是针对高轨道飞行器或地面发射近空间高超声速飞行器,对空射近空间飞行器助推弹道的研究很少。

本文主要是针对空射近空间飞行器助推弹道规划问题,结合各飞行段特点,建立多段多约束参数化助推弹道规划模型,提出了一种适应于工程应用的助推弹道规划方法,该方法具有很高的求解精度和较快的求解速度,易于工程实现,具有较高工程应用价值。

1 数学描述

1.1 运动方程的建立

为了便于研究,假设地球为均质不旋转圆球并忽略附加哥氏力的影响,根据火箭受力情况可得到运动方程:

(1)

式中:v为飞行速度;Fp为发动机推力;Fx,Fy,Fz分别为气动阻力、升力和侧向力;α,β分别为攻角和侧滑角;θ为速度倾角;ψ为速度偏角;γ为倾斜角;x,y,z为位置三分量;m为飞行器质量;qm为质量流量。

1.2 约束条件参数化模型

空射模式为载机在空中投放运载器后,运载器在一定初速下点火加速并利用气动力和推力迅速拉起,同时近空间飞行器交班点高度较低,助推段弹道相对运载器或弹道导弹飞行高度较低,转弯幅度较大,所以在弹道设计时需要考虑过载、控制、子级分离要求和交班点参数要求等约束。

①载荷约束。火箭从飞机投放后,一级发动机点火加速快速拉起。火箭一级飞行主要是在稠密大气中完成,同时拉起过程中需采用大过载。考虑火箭结构及发动机承载能力,需要对飞行法向过载进行约束,即

(2)

式中:ny为法向过载,Fy1为法向力,nmax为火箭所能承受的最大法向过载。

②控制约束。火箭投放后进入一级飞行段,一级飞行在稠密大气层完成,并需要在较短时间采用大攻角快速拉起弹道,由于载荷和控制能力的限制,需要对飞行攻角加以限制;二级飞行段飞行高度相对较高,主要考虑控制能力对调姿角速度的适应性,需要对角速度进行限制,同时考虑二级能量管理对侧滑角的约束:

(3)

式中:t1为一级点火时间,t2为一级关机时间,t3为二级点火时间,tT为二级关机点时间;αmax1,αmax2分别为一级飞行段和二级飞行段最大可用攻角;βmax为二级飞行段最大可用侧滑角;ωcx,max为一、二级姿态角调节角速度最大值。

③子级分离点参数约束。子级分离点参数要求主要包括两方面:一方面是分离时刻姿态要求和姿态角速度要求,该要求可通过控制变量参数化建模来保证;另一方面,由于一子级分离在大气层内进行,分离高度过低会导致分离气动干扰过大,控制系统难以适应,因此需要对分离高度进行限制,即

h(t3)≥hC

(4)

式中:hC为一、二级分离点最低高度。

④终端约束。助推段弹道终端参数需满足交班点高度、速度、速度倾角和速度偏角等要求,即

(5)

2 弹道规划方法

2.1 控制变量参数化建模

为了实现火箭投放后快速爬升,一级采用最大过载快速拉起。为了保证低弹道入轨条件,在二级纵向剖面进行程序角参数化设计;为了满足不同交班速度需求,在二级横向剖面进行能量管理设计。基于以上考虑,近空间飞行器助推段飞行程序参数化模型可描述如下。

①投放段攻角设计。

该段主要是为了保证飞机和运载火箭安全分离,一般采用定攻角飞行,即

α(t)=α0,t∈(0,t1)

(6)

式中:α0根据飞行器气动控制特性选择。

②一级飞行段攻角设计。

对于空中发射,运载火箭一般采用水平投放。为了减小助推段速度损失,火箭水平投放后需要快速拉起爬升穿越稠密大气层,所以在一级攻角设计时,尽量采用火箭所能承受的最大过载对应的攻角飞行,实现火箭快速拉起爬升。这种情况下跨声速段大攻角飞行气动干扰问题靠火箭自身控制能力来保证。

(7)

式中:CN为法向力系数,ρ为大气密度,h为飞行高度,Ma为飞行马赫数,Sr为气动参考面积,δm为火箭喷管摆角;t2s为大攻角拉起结束时间,t2为一级关机点时间,t2s≤t2。

③一级滑行段攻角设计。

该段主要用于调整交班点速度倾角,同时保证一、二级分离高度。

α(t)=αhx,t∈(t2,t3]

(8)

式中:αhx为一级滑翔段飞行攻角,一般取αhx=0,thx=t3-t2,表示一级滑行时间。

④二级飞行段攻角设计。

二级飞行段攻角设计如下:

(9)

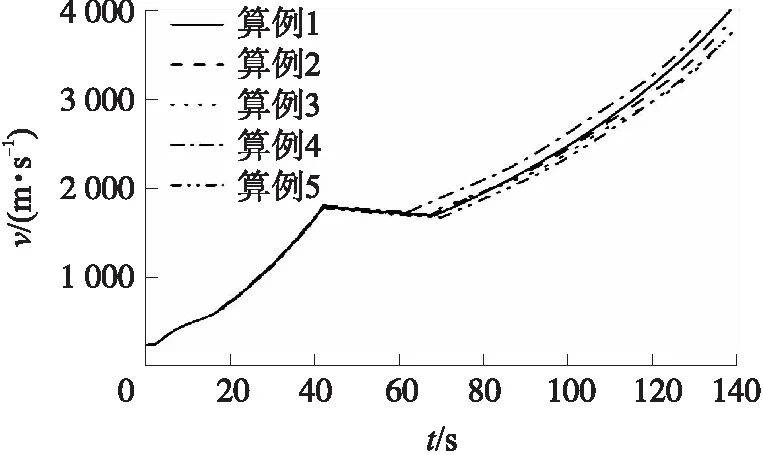
式中:t3为二级点火时间;t4,t5,t6为设计时间。αm为二级飞行最大攻角,αT为要求的交班点攻角。ωcx为二级攻角调节角速度。取tT为二级关机点时间,则t6

⑤二级能量管理侧滑角设计。

为了实现近空间飞行器不同交班条件需求,在二级进行能量管理[10]。为了不影响二级纵向控制交班点精度,考虑在二级通过调整侧滑角实现能量管理,其中侧滑角设计如图1所示。

(10)

式中:βm为二级能量管理最大侧滑角;t0,tm分别为二级能量管理起始时间和结束时间;tb为侧滑角切换时间。

图1 能量管理侧滑角参数化模型

基于以上飞行参数化模型,选取一级大攻角拉起结束时间t2s,一级滑行时间thx,二级飞行最大攻角αm,二级攻角调节角速度ωcx,二级能量管理最大侧滑角βm及侧滑角切换时间tb等为设计变量。

考虑助推段结束点交班高度、速度、速度倾角以及速度偏角误差的要求,助推段弹道规划可表述为在考虑的约束条件下对以下非线性方程组求解:

(11)

式中:Δh,Δv,Δθ,Δψ分别为交班点高度偏差、速度偏差、速度倾角偏差和速度偏角偏差。

2.2 基于粒子群的弹道规划方法

粒子群算法是一种基于群体智能的优化方法,采用的是速度和位移模式,每个粒子的位置对应一个解,而解的目标函数值作为判定粒子位置优劣的准则。粒子群算法由于具有收敛速度快、易于实现的特点,所以在飞行器优化领域得到了广泛的应用。

①优化变量。

基于2.1节中参数化建模,空射近空间飞行器助推弹道优化设计变量为

X=(αmβmt2sωcxthxtb)T

(12)

②目标函数。

本文研究空射模式近空间飞行器助推弹道规划问题,同时还考虑二级能量管理,因此将交班点参数偏差作为目标函数,即

J(X)=min(J1+J2+J3+J4)

(13)

式中:J1=λ1Δh,J2=λ2Δv,J3=λ3Δθ,J4=λ4Δψ;λ1,λ2,λ3,λ4为调节系数,通过调节其取值,使得J1,J2,J3,J4量级一致。

③弹道规划。

假设Xi=(αm,iβm,it2s,iωcx,ithx,itb,i)T为弹道解算中的一个解,其为粒子群优化算法中的一个粒子,那么在每次搜索中,多个粒子即构成粒子群。根据标准粒子群算法,粒子位置和速度的更新公式如下:

(14)

传统粒子群优化算法存在搜索速度慢,容易陷入局部最优等缺点。研究表明,异步时变学习因子与线性递减惯性权重配合使用效果较好[11],同时为了克服线性权重不能充分协调全局和局部搜索性能的不足[12],本文采用非线性递减策略调整惯性权重值。在优化过程中,惯性权重和学习因子取值如下:

(15)

3 仿真分析

表1 仿真约束条件

表2 不同状态终端约束条件

基于给定的初始参数及约束条件,通过弹道规划解算,本文给出了5组仿真算例,每组仿真算例对交班条件需求不同,弹道规划控制参数仿真结果如表3所示,弹道规划仿真结果如表4所示。

表3 不同状态控制参数优化结果

表4 不同状态规划仿真结果

弹道规划仿真结果典型弹道参数曲线如图2～图6所示。

图2 高度随时间变化曲线

图3 速度随时间变化曲线

图4 速度倾角随时间变化曲线

图5 速度偏角随时间变化曲线

图6 法向过载随时间变化曲线

从以上仿真分析可知,对应不同交班条件要求,规划结果均满足过载、控制及分离等约束和交班点参数要求,其中交班速度精度小于1 m/s,交班高度精度小于2 m,交班速度倾角精度小于0.01°,交班速度偏角精度小于0.01°,可适应不同交班速度的要求。

综上分析,本文研究的助推段弹道规划方法可实现多约束下的助推段弹道规划,并可通过能量管理满足不同交班速度要求。

4 结论

本文针对空射近空间飞行器低弹道快速入轨弹道规划问题,提出了一种适应于工程应用的弹道快速规划方法,该方法能快速获得满足不同交班速度需求的参考弹道。仿真结果表明:交班速度精度小于1 m/s,交班高度精度小于2 m,交班速度倾角精度小于0.01°,交班速度偏角精度小于0.01°;全程过载、控制及分离等过程约束均满足要求。该方法具有很高的精度和较快的速度,易于工程实现,具有较高工程应用价值,可为空射近空间飞行器方案论证和初步设计提供参考。