壳体刻槽PELE冲击破碎数值模拟
程 春,杜忠华,陈 曦,徐立志,隋红霞,徐同昆
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.黑龙江北方工具有限公司,黑龙江 牡丹江 157013)
横向效应侵彻弹丸(penetrator with lateral effect,PELE)撞击靶板瞬间,外壳受到剧烈冲击载荷作用,外壳材料内部存在自身缺陷及动能的快速沉积,导致微裂纹或孔洞的萌生、传播及联通;贯穿靶板过程中,外壳材料内壁还受到装填物膨胀产生的径向作用力以及靶板对外壳的径向束缚作用;穿透靶板之后,靶板对外壳的径向束缚作用消失,带有损伤的外壳在装填物径向作用力下发生进一步破碎飞散[1]。对于大口径PELE,在壳体上适当预制切缝可提高弹丸对混凝土靶的开孔效果[2]。同理,为控制PELE贯穿金属靶板之后的破碎效果,提高弹丸对靶后目标的毁伤能力,可以在壳体上预制刻槽。本文设计一种壳体外表面刻有V形纵向槽的PELE,利用均匀设计方法确定刻槽数量、刻槽角度、刻槽深度因素水平表,利用数值模拟方法分析壳体的冲击破碎情况,得到刻槽参数对壳体破碎的影响规律。
PELE壳体材料的破碎问题属于固体材料的冲击破碎问题。目前,模拟材料冲击破碎的方法主要有有限元法、离散元法、水平集方法、分子动力学方法、光滑粒子流体动力学方法等。其中,1995年Benz等提出了适用于模拟固体材料的光滑粒子流体动力学(SPH)方法[3],该方法支持材料大变形,能够跟踪拉格朗日状态变量,避免了计算中因网格畸变导致的计算终止,因此在模拟断裂和破碎等材料的动态响应方面具有非常大的吸引力[4~5]。Kong等用SPH方法数值模拟带端盖圆柱壳在爆炸载荷作用下的破碎过程,得到了与试验吻合较好的碎片尺寸分布和质量分布[6]。
本文采用SPH方法,利用Johnson-Cook本构模型,引入最大主应力失效和随机失效准则,建立数值模拟模型,模拟PELE壳体贯穿金属靶板的冲击破碎,并通过穿甲试验验证数值模拟模型的有效性。
1 数值模拟模型
1.1 壳体的本构模型
PELE壳体材料采用钨合金,本文采用Johnson-Cook本构模型来描述PELE侵彻靶板过程中钨合金壳体的变形和碎裂行为。
Johnson-Cook本构模型表达式[7]:
(1)
式中:σeq为等效应力;n为应变强化指数;A为参考应变率和温度下材料的屈服强度;B,C,m分别为应变强化系数、应变率敏感系数和温度软化系数;ε0为参考应变率。
T*=(T-To)/(Tm-To)
(2)
式中:T,To,Tm分别为材料的实际温度、环境温度和材料熔化温度。
钨合金材料主要参数[8-9]见表1。表中,ρ,μ,E,Y分别为钨合金材料的密度、泊松比、弹性模量和屈服强度。

表1 钨合金的主要材料参数
1.2 最大主应力失效准则
文献[10]在研究钨合金的温度效应和应变率效应时发现,随着应变率增大,钨合金材料的延性降低,脆性提高。文献[11]通过分析钨合金的断裂路径和试件断裂表面的扫描电子显微镜图像发现,95W-3.5Ni-l.5Fe呈现脆性断裂,初始裂纹产生于W-W颗粒边界和钨颗粒中。基于钨合金尤其是高密度钨合金在动态加载条件下呈现出脆性断裂行为,对PELE的钨合金壳体的断裂破碎模拟时,在Johnson-Cook本构模型的基础上添加描述脆性材料破坏的拉伸主应力失效准则。文献[12]根据最大拉伸应力准则确定材料的损伤临界值,在数值模型中获得裂解行为,包括微观裂纹的萌生、扩展,以及近似等距的表面裂纹的形成,取得了很好的效果。因此在模拟钨合金壳体的断裂时,添加拉伸主应力失效准则具有必要性和可行性。
1.3 随机失效模型
由于壳体破碎是随机的,产生的破片具有明显的概率统计特征,但是在数值模拟时壳体的结构和材料是均匀的,材料属性是唯一的,因此为了模拟壳体破碎的随机特性,数值模拟时在拉伸主应力失效的基础上,引入基于Mott理论建立的Stochastic随机破坏模型[13]。该模型将圆柱壳体按径向截面简化为二维圆环,假设应变从ε变化到ε+dε时,沿环向单位长度壳体发生断裂的概率为
dP=Deγεdε
(3)
式中:P为发生断裂的概率;D,γ为与加载应变率有关的材料特性参数。根据式(3),随着ε的增加,断裂发生的概率按指数规律增大。假设应变为ε时,壳体未断裂的概率为1-P,则应变增加dε时,壳体发生断裂的概率为
dP=(1-P)Deγεdε
(4)
积分求解,可得壳体某位置达到塑性应变ε之前发生断裂的概率:
(5)
(6)
则断裂应变的均方根(标准差):
(7)
在利用Stochastic随机破坏模型进行数值模拟时,给定材料的断裂应变值εf(真实应变),并在每一个壳体单元中设置一个符合Mott随机分布的比值,该比值是某单元发生断裂时的应变与断裂应变εf之比。
1.4 模型验证
为验证数值模拟模型和材料参数选择的合理性,选取文献[1]中的某些试验工况进行数值模拟,并对比数值模拟结果和试验结果。PELE壳体材料为钨合金,直径10 mm,长度50 mm,装填物材料分别为低密度铝合金和聚乙烯,直径和长度分别为6 mm和45 mm,靶板材料为8 mm厚铝合金,弹丸着靶速度分别为1 254 m/s和1 258 m/s,数值模拟的结果和试验中X光拍摄到的壳体穿透靶板之后的破碎情况如图1所示。由图1可见,数值模拟结果和试验结果非常相似。

图1 试验结果和数值模拟结果的对比
当弹丸装填物材料分别为低密度铝合金和聚乙烯,撞击速度分别为1 254 m/s和1 258 m/s时,试验得到壳体剩余速度分别为1 208 m/s,1 203 m/s,碎片最大径向飞行速度分别为221 m/s,184 m/s,数值模拟得到的剩余壳体速度分别为1 216.39 m/s,1 209.56 m/s,碎片的最大径向飞散速度分别为220.38 m/s,190.47 m/s。4个对比项的误差分别为0.69%,0.28%,0.55%,3.52%,误差非常小,这说明数值模拟结果和试验结果吻合良好。
为进一步验证试验模型的有效性,开展PELE穿透Q235钢板之后的碎片收集试验,试验用弹丸壳体直径为8.8 mm,长度为40 mm,装填物直径为5.5 mm,长度为36 mm。弹芯和壳体材料分别为尼龙和钨合金,Q235钢板厚度为2 mm。试验用水箱收集撞击后的碎片,为避免碎片发生二次破碎,水箱面对炮口的一面材料为50 mm厚泡沫,其余各面为5 mm厚45#钢。当弹丸着靶速度为1 003.8 m/s时,数值仿真得到的弹体破碎情况和试验收集的碎片如图2所示。图2中碎片的形状及尺寸分布显示,数值模拟结果和试验结果吻合较好,再次验证了数值模拟模型的有效性。

图2 数值模拟结果和试验收集的碎片对比
2 壳体刻槽PELE数值模拟结果与讨论
未刻槽PELE示意图如图3所示,弹丸外径de=10 mm,长度lp=40 mm,装填物直径di=6 mm,长度lc=35 mm。弹丸壳体和装填物材料分别为钨合金、尼龙。

图3 未刻槽PELE示意图
均匀设计试验方法能够在全部试验点中选出充分均匀分散且具有代表性的试验点,反映所要研究体系的特征,大大减少试验次数。本文利用均匀试验方法研究刻槽数量、刻槽角度、刻槽深度对壳体破碎的影响。刻槽之后的弹丸壳体截面示意图如图4所示。

图4 刻槽弹丸壳体截面示意图
弹丸壳体上的预制刻槽为V形槽,V形槽的角度为α,深度为h,在弹丸壳体的截面上均匀排布s个V形槽。采用3因素7水平均匀设计试验,选用U7(74)均匀试验设计表。因素水平表如表2所示。
根据试验因素水平表,设计7次试验,每次试验的参数组合见表3。利用数值模拟得到各次试验的壳体破碎情况,弹丸着靶速度为1 000 m/s,靶板为5 mm厚铝合金(型号为2A12)。考虑到弹丸对靶后目标的毁伤主要依靠剩余壳体和壳体破碎产生的碎片,而对靶板目标的毁伤面积主要取决于分散的碎片, 本文以弹丸对靶后目标的大面积毁伤为研究目标,定义弹丸产生的1 mg以上的碎片质量占壳体总质量的比值K为壳体破碎程度的衡量指标,数值模拟方案及K值如表3所示,数值模拟结果如图5所示。
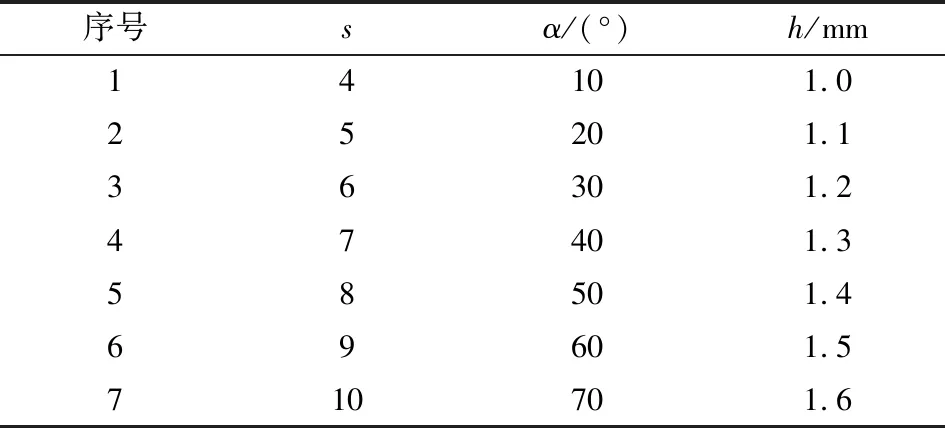
表2 因素水平表

表3 数值模拟方案及K值

图5 数值模拟结果
从图5数值模拟结果可以看出,弹丸壳体的纵向断裂沿着刻槽位置开始,壳体破碎产生的碎片多为长条状,碎片宽度与刻槽数量密切相关,刻槽数量越多破片宽度越小。利用回归分析方法得到壳体破碎程度K和刻槽数量s、刻槽角度α、刻槽深度h的回归方程:
K=0.052 0+0.149 4s-0.002 3α-0.350 3h-0.014 6s2+0.056 5sh
(8)
计算得到相关系数R=0.982 7,F检验值为F=11.364 2,取显著水平0.05,查表得到F(3,3)=9.28,F>F(3,3),说明回归方程及回归系数显著。
从回归方程可以看出,壳体破碎程度随刻槽数量的变化呈抛物线趋势变化,在一定数量范围内,壳体破碎程度随刻槽数量的增大,先增大后减小。刻槽数量过小,壳体应力集中不明显,壳体产生断裂裂纹需要的能量增加,壳体破碎程度低;刻槽数量过多,壳体破碎集中于壳体头部,头部碎片飞散消耗大量能量,导致壳体破碎不完全。刻槽角度在10°~70°范围内,随着刻槽角度的增大,刻槽引起的应力集中现象减弱,壳体破碎程度随刻槽角度的增大而减小。刻槽深度影响壳体纵向裂纹的传播,当壳体深度较大时,壳体上产生较长的纵向裂纹,裂纹传播消耗能量,如果径向裂纹需要的能量不足,则壳体不能产生大量碎片。壳体破碎程度与预制刻槽数量、预制刻槽深度的乘积正相关。
3 结论
本文在分析了钨合金材料动态断裂特点的基础上,采用SPH方法,利用Johnson-Cook本构模型,引入最大主应力失效和随机失效准则,建立数值模拟模型,模拟PELE壳体的冲击破碎。利用均匀设计方法确定刻槽数量、刻槽角度、刻槽深度的因素水平表和数值模拟方案;分析不同刻槽参数条件下壳体的破碎情况,利用回归分析得到了刻槽参数与壳体破碎程度之间的函数关系,主要结论如下。
①通过数值模拟对比试验,数值模拟的结果和试验结果吻合得非常好,这充分说明了壳体数值模拟模型和材料参数选择的合理性,说明本文采用的数值模拟模型可用于模拟壳体刻槽PELE的冲击破碎。
②弹丸壳体的纵向断裂和破碎沿着刻槽位置开始,壳体破碎产生的碎片多为长条状;要提高弹丸的靶后高效毁伤能力,控制弹丸破片的数量和分散情况,在弹丸壳体上刻槽是一种有效的方法。
③预制刻槽数量、角度、深度是影响壳体刻槽PELE穿透靶板之后碎裂的的3个重要因素;弹丸壳体破碎程度随预制刻槽数量的增大先增大后减小,随角度的增大而减小,同时与数量、深度的乘积正相关。

