回转式弹仓的自适应近似变结构控制

王 锴,尹 强,羊 柳

(南京理工大学 机械工程学院,江苏 南京 210094)

回转式弹仓对于火炮自动装填系统来说是十分重要的一个分系统,回转式弹仓通过永磁同步电机提供动力源,在电机的旋转下通过减速箱带动弹仓的链条转动,将待射击弹丸旋转至取弹口。如果弹仓控制精度低将导致机械手取弹失败,造成安全隐患,因此弹仓的工作性能将直接影响火炮自动装填系统能否顺利完成射击任务。因此,提升回转式弹仓的控制精度并降低其在运动过程中的振动将存在重要意义。回转式弹仓由弹筒、链轮、链条、导轨、基座等组成,是一类具有大惯量变化及系统参数具有不确定性特点的系统,其运动控制具有一定的难度。邹权等[1]提出了一种带有积分型滑模面的自适应鲁棒控制算法,在理论上证明了其提出的算法具有更好的动态性能及稳态性能。侯保林等[2]提出了一种基于线性矩阵不等式(LMI)的鲁棒控制算法,即最优保性能控制算法,并验证了算法具有高的控制精度。岳才成等[3-4]针对链式弹仓提出了一种基于指数趋近律的滑模控制方法,引入模糊自适应算法,实现了系统的精确定位,有效抑制了趋近过程的振动。李杰等[5]针对非线性自抗扰控制在实际应用中的困难等问题,提出了一种线性/非线性自抗扰控制切换控制方法,解决了非线性自抗扰控制在参数整定、稳定性分析等方面的困难。薛生辉等[6]针对比例-积分控制因不能预测未来输出而提前改变控制量,从而在用于光电稳定伺服系统时往往响应剧烈的问题,提出了一种新型的基于PI(比例(proportion)、积分(integral))增量和GPS增量加权的比例积分控制加广义预测控制算法,实现了基于历史、当前和未来偏差计算控制量,通过仿真验证了该方法的精度、平稳性及快速性。郑美茹等[7]针对永磁同步电机的传统滑模控制技术中趋近速度与振动程度之间存在矛盾的问题,利用分数阶积分型符号函数的特性,设计基于分数阶的积分时变滑模变结构控制器,达到了在振动程度较小的前提下提高系统响应速度的目的,仿真和实验结果证明了该方法的强鲁棒性及快速性与准确性。叶镭等[8-9]针对炮控系统不确定性参数,提出了一种基于自抗扰控制的解耦方法,这种方法能够有效抵抗系统的不确定非线性因素,并验证了其强鲁棒性和有效性。上述文献中所提出的控制算法均取得了比较满意的控制效果,在以上研究成果的启发下,本文针对火炮弹仓运动过程中弹仓出现振动、控制精度不高、非线性摩擦以及冲击等问题,提出一种改进自适应近似变结构控制算法(improved adaptive approximation variable structure,IAAVS)以提高控制精度并降低系统振动。

滑模变结构控制表现出强鲁棒性,利用滑模变结构控制对系统参数扰动不敏感的特性,可以提高控制系统的性能[10]。但是,一般的变结构控制律都是不连续的,从而不可导。控制信号的不连续是由控制律中所含继电控制项引起的,易形成控制信号的颤振,具有不连续控制律的滑模变结构控制在实际使用中不易实现,并且影响控制系统的使用寿命。本文用连续可导的控制律替代传统滑模不连续可导控制律,运用自适应算法,依据系统状态进行切换函数的自适应改变;在运动规划方面引入三角函数规划法,使规划运动的轨迹连续光滑且连续可导。仿真结果表明,该方法具有很高的控制精度,并且明显降低了振动。

1 系统描述与数学建模

回转式自动化弹仓由永磁同步电机提供动力,永磁同步电机采用力矩控制方式。鉴于电机本身的设计特点,本文忽略电流环影响,不再考虑电机内部对电机控制的影响。由于弹仓系统构件繁多,对其进行合理化简化,将弹仓系统所有构件视为刚体,将弹仓运动过程中的物理参量等效到永磁同步电机的转子轴上,取电机转子为等效构件,系统动能方程为

(1)

式中:Jeq为系统的等效转动惯量;Ja为永磁同步电机转子的转动惯量;Jb为减速箱的等效转动惯量;Jci和ωci分别为第i个链轮的转动惯量和角速度;x为链轮总数;ω为永磁同步电机转子实际角速度;Jdj和ωdj分别为第j个弹筒(含弹丸)的转动惯量和角速度,n1为旋转运动弹筒(含弹丸)的个数;mdk和vdk分别为直线运动的第k个弹筒(含弹丸)的质量和质心速度,n2为直线运动的弹筒(含弹丸)的个数;Jef和ωef分别为第f个链节的转动惯量和角速度,x1为旋转运动链节的个数;meβ和veβ分别为第β个作直线运动的链节的质量和质心速度,x2为直线运动链节的个数。对式(1)进行化简,得:

(2)

在运动过程中,回转式弹仓各部件之间会产生一定的阻尼力,现将系统阻尼力等效到永磁同步电机的等效转子上,得到等效力的方程:

(3)

式中:Beq为系统的等效阻尼系数;Ba为同步电机的等效阻尼系数;Bb为减速箱的等效阻尼系数;Bci,θci分别为第i个链轮的阻尼系数、电机转子转动一圈时链轮的角位移;Bdj,θdj分别为第j个弹筒(含弹丸)的黏性阻尼系数、电机转子转动一圈时的角位移;Ddk,Ldk分别为第k个做直线运动的弹筒(含弹丸)的黏性阻尼系数、直线位移;Bef,ωef,θef分别为第f个链节的黏性阻尼系数、角速度、电机转子旋转一圈时的角位移;Deβ,veβ,Leβ分别为第β个做直线运动的链节的黏性阻尼系数、速度以及位移。对式(3)进行化简,得:

(4)

回转式自动化弹仓的动力学方程为

(5)

图1 期望轨迹

2 改进的自适应近似变结构控制

定义系统的位置跟踪误差e:

e=θ-θd

(6)

式中:θd为弹仓实际角位移。

对于设计的有界的控制输入,实验的目标就是使电机转子的位移θd能够很好地跟踪期望轨迹的位移曲线θ,且产生的跟踪误差尽量小,以提高系统性能。

本文中,切换函数采用积分型滑模函数,并采用自适应算法对切换函数进行改变,定义滑动超平面Q:

(7)

式中:A为待定系数,λ为滑模面参数,且A>0,λ>0。

由式(5)、式(6)和式(7)得:

(8)

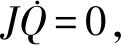
(9)

由于系统的不确定扰动不可能为0,遂增加切换控制项us以平衡系统的不确定扰动,切换控制项为

us=-ηsgns

(10)

式中:η为切换项增益,且η>0,sgns为符号函数,定义如下:

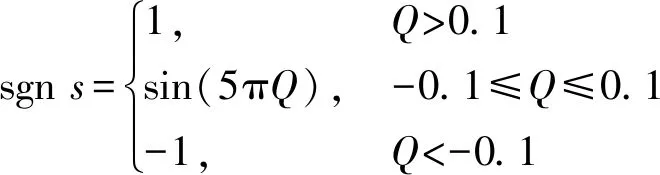
(11)

同时为了提高系统的控制稳定性,增加鲁棒控制项uk:

uk=-yQ

(12)

式中:y为待定系数,且y>0。

得系统的控制律u:

(13)

稳定性分析,定义Lyapunov函数V1:

(14)

将式(14)对时间求导,并将式(6)、式(8)、式(13)代入,得:

(15)

根据式(10),存在合适的A,y,η使得式(15)为

(16)

(17)

(18)

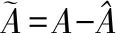
(19)

所以系统的控制律改写为

(20)

定义如下的Lyapunov函数V2:

(21)

式中:γ1,γ2,γ3为待定系数,且γ1>0,γ2>0,γ3>0。将式(18)对时间求导,并将式(17)的控制律u代入得:

(22)

(23)

将式(20)代入式(19),得:

(24)

即可设计合适的系统参数使得系统具备达到滑模面的条件并保持稳定。

3 仿真分析与验证

由于弹仓系统携带弹丸数量比较多,弹丸数量变化情况多,所以本文只对3种情形进行研究,即空载(弹筒不装弹丸)、半载(装载一半弹丸且相邻排列)、满载(弹筒内全部装载弹丸),不同载荷条件下的等效转动惯量J与等效阻尼系数B如表1所示。

表1 等效转动惯量及等效阻尼系数

从图2可以得出:改进后的自适应近似变结构控制器与传统自适应滑模控制器的位置跟踪误差几乎为0,控制效果明显优于PID控制器的跟踪效果;PID的控制误差维持在-0.121～0.1 rad。现将改进后的自适应近似变结构控制与传统自适应滑模控制器的位置跟踪效果进行放大对比,结果如图3所示。从图3可以得出,传统的自适应滑模控制的位置控制误差在系统起始阶段出现小幅振动。图3(b)为仿真曲线的局部放大图。在整个过程中振动比较剧烈且位置误差收敛在-2.5×10-4～2.5×10-4rad;改进自适应近似变结构控制在系统初始阶段控制误差为0,在加入等效扰动以后,位置误差出现很小的波动,且曲线较平滑,将位置误差保持在-1.31×10-4～1.31×10-4rad之间,位置控制效果明显优于传统自适应滑模控制,这表明改进后的自适应近似变结构控制,通过运用连续控制律代替传统不连续控制律并且对切换函数进行自适应调整的方法,在位置跟踪误差方面具有明显的优势以及降低振动的效果。

图2 3种不同控制方法(满载)同种工况下控制误差对比

图3 IAAVS与ASMC同种工况下控制误差对比

图4为回转式弹仓在分别应用PID、ASMC与IAAVS 3种控制方法时控制输入u的对比图。从图4(b)中可以得出,回转式弹仓在应用ASMC控制方法时,控制输入u出现了明显的振动现象;从图4(a)中可以得出,回转式弹仓在应用IAAVS、PID 2种控制方法时,弹仓的控制输入u曲线相对ASMC控制输入u更加平滑,未出现振动现象。因此,结合位置跟踪误差e曲线与控制输入u曲线可以得出,改进自适应近似变结构控制方法更适用于回转式弹仓的定位控制,有效降低了弹仓位置跟踪误差,降低了弹仓控制输入u的振动,具有很好的鲁棒性及精确性。

图4 3种不同控制方法(满载)同种工况下控制输入u

图5为回转式弹仓空载、半载、满载时位置控制误差对比。从图5可以看出,弹仓在空载、半载、满载3种状态下的位置跟踪误差基本相同,误差保持在-1.5×10-4～1.5×10-4rad之间,说明了本文所提方法对于不同载荷条件下的弹仓运动控制具有很好的一致性,仿真结果满足系统对于误差的要求。

图5 IAAVS 3种工况位置跟踪误差

图6给出了弹仓在空载、半载、满载3种工作状态下的控制输入曲线。从图6中可以看出,弹仓在3种工作状态下的控制输入曲线都很平滑,没有出现振动现象,易于在实际实验中实现。

空载、半载、满载情况下的参数A随时间的变化如图7所示。从图7中可以看出,在系统未受到外部扰动之前,切换函数参数A的值稳定于1,随着外部扰动的施加,切换函数参数A的数值依据自适应律进行自适应改变,以满足系统降低振动提高控制精度的要求;当外部扰动消失时,切换函数参数A又稳定于初始值。

图6 IAAVS 3种工况控制输入

图7 A的估计值

图8 J的估计值

图9 B的估计值

综上所述,本文提出的改进自适应近似变结构控制算法,使回转式弹仓系统具有很高的位置跟踪精度并且能够很好地抑制系统参数变化和外部不确定扰动对弹仓系统的影响,得出的控制力矩曲线光滑不振动,有利于在实验中实现。

4 结论

回转式自动化弹仓系统是一类具有系统不确定参数、等效转动惯量以及系统等效阻尼系数都会随着系统工作状态发生变化的系统,同时还要考虑链传动引起的多边形效应以及系统摩擦对于位置控制精度的影响,本文主要工作包括:

①提出一种改进的自适应近似变结构控制,采用连续可导的切换控制率代替传统不连续的控制律,在控制律中引入三角函数,使控制律变化平缓,不产生突变;

②提出对切换函数设置估计参数,使其能够依据系统状态进行切换函数的在线调整,采用自适应算法估计系统参数的变化,以满足系统运动要求;

③对弹仓运动角加速度进行了优化设计,使弹仓在满足时序要求的前提下运动更加平稳且弹仓在空载、半载、满载条件下运动控制具有一致性。

本文对弹仓控制系统的改进,不仅有效降低了系统的振动而且明显提高了位置控制精度。回转式自动化弹仓在空载、半载、满载3种工作状态下的仿真结果表明,提出的改进自适应近似变结构控制方法具有很好的鲁棒性和控制精度。