无处不在的轴对称

☉江苏省南京师范大学盐城实验学校 罗 俊

轴对称是图形变换之一，旨在培养学生从运动的角度去观察、认识图形.轴对称有许多重要的性质，如：对称轴两旁的图形全等，对应线段相等，对应角相等；对称点的连线被对称轴垂直平分；对应边若相交，交点一定在对称轴上，对应边与对称轴的夹角相等等.利用轴对称的这些性质不仅可以解决数学自身的一些问题，而且在实际的生产、生活中也有广泛的应用，可以说，轴对称在生活无处不在，随处可见.

一、利用轴对称简化计算

在数与式的混合运算中，简化计算的方法包括：利用加法交换律、加法结合律、乘法交换律、乘法结合律或乘法分配律简化计算；利用平方差公式或完全平方公式简化计算；利用分组、拆项、添项简化计算等.当一列数整齐地排列在一个轴对称图形中时，我们也可以利用轴对称的性质简化计算.

例1如图1，放在正方形内的五列数，认真观察它们的排列规律，怎样用简便的方法计算出它们的和？

分析：正方形是轴对称图形，它有四条对称轴.若沿着数字5所在的对角线折叠，发现在对称位置上的两个数之和均为10，这样就使运算大为简化.

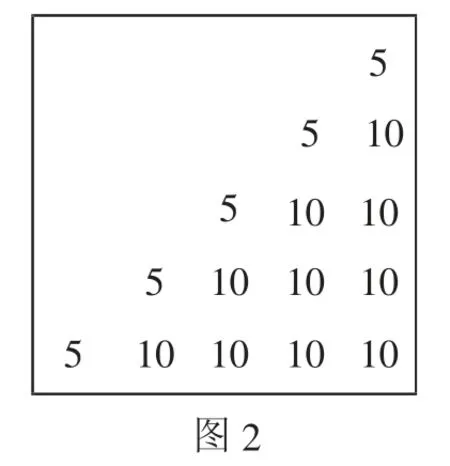
解：让正方形沿数字5所在的直线折叠，并让对称位置上的数字相加得到图2，于是所有数字的和等于5×5+10×10=125.

点评：因为正方形是轴对称图形，所以沿对称轴折叠后，对称轴两旁的部分能够互相重合，这是此题能简便计算的主要原因.

二、利用轴对称找到最短路线.

两点之间的最短路径就是这两点之间的线段，点到直线的最短路径就是点到直线的垂线段，平行线间的最短路径是一条直线上任一点到另一条直线的垂线段.那么一条直线同侧的两个固定点到该直线上一动点的最短路线又如何确定呢？利用轴对称可以轻松解决.

例2如图3，OX、OY是两条公路，在两条公路夹角的内部有一油库A，现在想在两条公路上建两个加油站，为使运油的油罐车从油库出发先到一加油站，再到另一加油站，最后回到油库的路程最短，问：两加油站应如何选址？

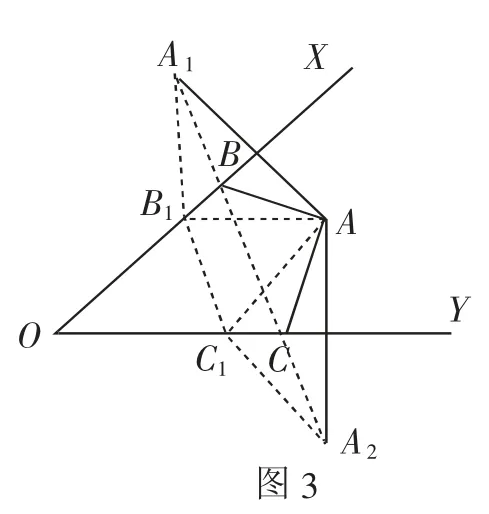
分析：上述问题可化为：在锐角XOY内部有一个点A，试作一个三角形，以A为一个顶点，另外两个顶点分别在OX、OY上，且使其周长最小.

解：如图3，分别取点A关于OX、OY的对称点A1、A2.连接A1A2分别交OX、OY于点B、C.则B、C两点即为加油站的位置.

点评：这里是利用轴对称化“折”为“直”，将三条线段放在同一直线上.若在OX、OY上另取两点B1、C1，根据“两点之间，线段最短”可得：A1A2＜A1B1+B1C1+C1A2.由轴对称的性质可得：AB+BC+AC＜AB1+B1C1+C1A.

三、利用轴对称设计图案

生活中许多精美图案都是利用图形变换设计的，如香港特别行政区区旗中间的紫荆花是利用旋转设计的，三菱汽车的标志是利用旋转设计的，一汽汽车的标志是利用轴对称设计的，奥迪汽车的标志是利用平移设计的等.利用轴对称设计图案，应首先确定对称轴，然后沿对称轴作轴对称图形即可.对称轴选择的不同，设计出的图案也会不同.

例3请在下列三个2×2的方格中，各画出一个三角形，要求所画三角形是图中三角形经过轴对称变换后得到的图形，且所画三角形的顶点与方格中的小正方形的顶点重合，并将所画三角形涂上阴影.（注：所画的三个图不能重复）

分析：可选择不同的直线作为对称轴，如水平的、竖直的或倾斜的，分别找到三角形三个顶点的对称点，然后连接即可得到对称图形.

解：如图5所示，以下方案可供选择.

点评：上述第一个与第三个图案以大正方形的对角线所在的直线为对称轴；第二个图案以大正方形水平中轴线为对称轴；第四个图案以下面矩形的水平中轴线为对称轴；第五个图案以大正方形竖直中轴线为对称轴.从这里可以看出，对对称轴的选择要灵活，这样可培养学生的发散性思维.

四、利用轴对称确定击球的方向

台球运动是一种室内体育运动，已在国际上广泛流行，主要是用球杆在桌面上击球，依靠得分的多少来决定比赛的输赢，台球与其他球类打法有些不同，如足球、篮球等都是把球直接送进球门或球框，而台球则要通过击打母球，然后由母球把目标球送进球洞才能得分，不仅如此，为了能连续打进球连续得分，必须在打进一个球之后，考虑母球能否停在理想的位置，以方便接着打下一个球.台球的打法有直击、搓球、跳球、反弹等.其中反弹就是将母球先击中桌面的边沿儿，母球反弹后击中目标球，要想实现这个目标，需要用轴对称确定击球方向.

例4如图6，四边形ABCD是长方形的台球桌面，有黑、白两球分别位于F、E两点的位置，试问：样撞击黑球F，才能使黑球先碰撞桌边DC，反弹后再击中白球E？

分析：若在桌边CD放上一面镜子，则镜中就有点E的影子E′，只要我们让黑球F对着影子E′打过去，就能反弹后击中白球E.这里的点E与点E′关于直线CD对称.

解：作点E关于直线CD的对称点E′，连接FE′，与CD的交点P即为撞击点.

点评：这是轴对称在打台球运动中的应用，它为我们击球确定了方向，当然在实战中不可能在边沿放一面镜子，然后我们对着镜子里的影子打，但其中的道理学生应该明白，使用反弹击球时，发挥空间想象能力，在脑海里作轴对称，然后对着目标球的对称点击球.

五、利用轴对称构造＂回文＂修辞和对联

文学中的“回文”修辞手法，是指把相同的字或词，在后文中倒过来放置，从而产生正读与反读都一样的效果，如风扇能扇风、奶牛产牛奶、清水池里池水清、雾锁山头山锁雾等.它们就像是一个个轴对称图形，距离对称轴等距离的位置上的字相同.古代还有回文对联，如：心清可品茶，茶品可清心；人过大佛寺，寺佛大过人等.原来文学家为了语言的精彩，还借用数学中的轴对称呢！

例5下列四句话中的文字有三句具有对称规律，其中没有这种规律的一句是（）.

A.上海自来水来自海上 B.有志者事竞成

C.清水池里池水清 D.蜜蜂酿蜂蜜

分析：根据四个选项的特点，分析出与其他三个不同的即为正确选项：A.上海自来水来自海上，可将“水”理解为对称轴，故A选项具有轴对称性；B.有志者事竞成，五字均不相同，所以不对称；C.清水池里池水清，可将“里”理解为对称轴，故本选项具有轴对称性；D.蜜蜂酿蜂蜜，可将“酿”理解为对称轴，故本选项具有轴对称性.故选B.

点评：汉语里的“回文”修辞，就是正着读与倒着读是一样的，如果从数学角度看就是具有轴对称的规律.其实，中国的传统文化——对联何尝不是对称呢？ 如：“万瓦千砖百匠造成十佛寺，一舟二橹四人摇过八仙桥”，数字对数字，事物对事物，对称美十分和谐；“青山有幸埋忠骨，白铁无辜铸佞臣”，“青山”对“白铁”，“有幸”对“无辜”，“埋忠骨”对“铸佞臣”.以这样工整的对称表达了人民的爱和恨.可见，对称美在文学方面也有生动、深刻的体现.

从上述事例中，我们可以看到，轴对称在数学运算、工程选址、台球运动、美术设计、语言文学等方面有重要的应用，因为轴对称从美学角度，就给人以平衡的美、匀称的美，它也符合中国古代建筑设计中的中轴线原则.只要大家在生活中注意留心观察，其实轴对称应用的事例远不止这些.