增设铺垫与渐次生长：磨题体会与建议——以两道一次函数初二期中习题为例

☉江苏省清江中学 张绍俊

期中考试常常由学校组织，很多试卷质量不高，原因是命题组织过程中的打磨与审卷环节做得不到位，所以不少学校的期中考试的组织很严密、规范，但是试卷的质量不高，影响了考试评价的信度与效度.笔者最近参与了一份期中试卷的打磨，对两道一次函数考题有了更深的理解.本文先记录这次磨题的经验，并跟进反思，供研讨.

一、两道一次函数题的磨题经历

案例1：一次函数图像信息题.

考题原型：为了缅怀先烈，继承遗志，某中学初二年级同学于4月初进行“清明雁栖湖，忆先烈功垂不朽”的定向越野活动.每个小组需要从点A出发，跑步到点B打卡（每小组打卡时间为1分钟），然后跑步到点C……最后到达终点（假设点A、B、C在一条直线上，且在行进过程中，每个小组跑步速度是不变的）.“文艺组”最先出发，过了一段时间后，“方程组”开始出发，两个小组恰好同时到达点C.若“方程组”出发的时间为x（单位：分钟），在点A到点C的行进过程中，“文艺组”与“方程组”之间的距离为y（单位：米）.它们的函数图像如图1：

A.当x=2时，“文艺组”恰好到达点B

B.“文艺组”的速度为150米/分钟，“方程组”的速度为200米/分钟，他们从点A出发的时间间隔为2分钟

C.图中点M表示“方程组”在点B打卡结束，开始向点C出发

D.出发点A到打卡点B的距离是600米，打卡点B到点C的距离是800米

思路简析：对照问题情境及图像上的数据信息，可以发现选项A、B、C中所解读出来的信息都是正确的、相容的（这种题型，通过几个选项之间的相容性审校，往往就能获得解答）.而选项D中两段路之和为1400米，而“方程组”总行程时间为7分钟，但有1分钟打卡，实际跑步时间6分钟，解读出“方程组”的速度是200米/分钟，这样总路程就是1200米，所以与选项D出现了矛盾、不相容的现象.

改编打磨：原题做下来，还是有一定的难度的.首先不是同时出发，而且先出发多长时间也不知道；另外，打卡的时间为1分钟，这里跟我们传统的行程问题的图表题又有所不同.所以，要解决这道题，需要很清楚地把握整个运动过程.作为选择题，使得这道考题的考查功能大打折扣，可以将这道考题研发成一道解答题，较好地体现学生对函数图像信息题的理解.我们可在原题的题干基础上，设计出以下一些问题：

（1）当x=__________时，“文艺组”恰好到达点B；当x=___________时，“方程组”从点B出发前往点C.

（2）“文艺组”和“方程组”的速度分别是多少？

（3）请你写出线段DN的解析式.

（4）求“文艺组”和“方程组”相距100米时的时间.

改编意图：第（1）小问做铺垫，提醒、帮助学生理解整个运动过程.第（2）问求速度，通常的题目中都是会求这个问题的，而且建立在理解了运动过程的基础上，（学生如果能答对前一问，就应该知道x=2时，“文艺组”恰好到达点B；当x=4时，“方程组”从点B出发前往点C.当然还有x=3时，“方程组”恰好到达点B）就应该知道求速度时分成两个运动过程，A—B，B—C，去寻找等量关系.当然，还可以求AB、BC甚至AC的距离，但是解答题的设问的数目不宜过多，而且学生能够求出速度，距离的求解肯定没有问题.另外（3）、（4）两问的设置主要考查一次函数的知识，而第（3）问先求解析式是为后续求解提供铺垫，主要是引导学生先求出点N的坐标，从而求出解析式，再解决第（4）问就轻松了.如果直接给出第（4）问，恐怕学生不知道利用一次函数来解决.

案例2：以一次函数为背景的新定义考题的打磨.

考题原型：在平面直角坐标系xOy中，对于任意点P（a，b）和直线y=ax+b，我们称直线y=ax+b为点P（a，b）的伴随直线，反之称点P（a，b）为直线y=ax+b的伴随点.特别的，直线y=b（b为常数）的伴随点为（0，b）.

如图2，已知△ABC三个顶点A、B、C 的坐标分别为（-2，-1）、（1，5）、（3，-1）.

（1）点A（-2，1）的伴随直线的解析式为_________（直接写出答案）；

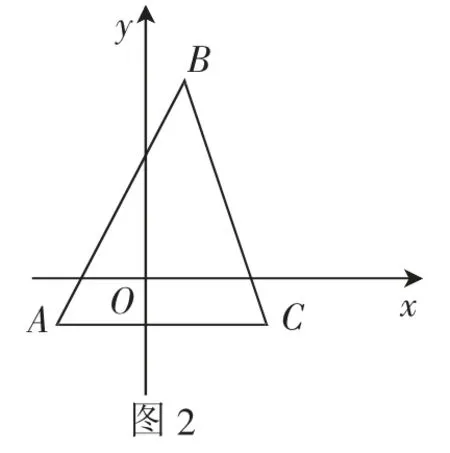
（2）若直线AB的伴随点是D，直线BC的伴随点是E，点F为x轴上的动点，当△DEF的周长最小时，求点F的坐标；

（3）点P是折线段A-B-C上的动点（包括端点A、C），若直线l是点P的伴随直线，当直线l与△ABC有且仅有两个公共点时，请直接写出点P的横坐标t的取值范围.

思路简析：第（1）、（2）问都是初步理解新定义，并不太难，第（3）问比较晦涩、难懂，而且需要考虑多个变量的取值范围，有较明显的区分作用.

打磨改编：对于第（1）问，新定义中有“特别的，直线y=b（b为常数）的伴随点为（0，b）”，所以我设想增加一个简单的小问，直线y=3的伴随点为_________，也为后面设想的第（2）问和第（3）问服务.

对于这题的第（2）问，有这样几个设想：

（1）若直线AB的伴随点是D，直线BC的伴随点是E，直线AC的伴随点是F，求△DEF的面积.

意图：考查学生在平面直角坐标系中利用割补法求三角形的面积.

（2）若直线AB的伴随点是点D，直线BC的伴随点是点E，点F为x轴上的动点，求|DE-DF|的最大值.

意图：考查学生对三角形三边关系的掌握.

（3）若直线AB的伴随点是点D，直线BC的伴随点是点E，点F为x轴上的动点，求|DE-DF|的最小值.

意图：绝对值的最小值为0，即当三角形为等腰三角形时即为所求.

（4）对于原题的第（3）问，点P是折线段B-A-C上的动点（包括端点A、C），若直线l是点P的伴随直线，设直线l与y轴的交点为M，求点P在折线段B-A-C上运动的过程中，点M运动的路径长.

当然原题最后一问对“动”直线经过“定点”的要求较高，如果学生对这种解题策略有所了解，也可一试，毕竟切入后续思路需要依靠这个狭窄的通道，如果不能顺利通过，则后续分析变量的取值范围就无从下手.命题打磨时对这类通道狭窄的设问要保持警惕，对于命题者来说，一定要防范出现个性化的理解或“命题任性”.

三、进一步的思考

1.习题改编功夫重在平时修炼精进

很多教师在“上级部门”安排一份试卷命题工作时，才会觉得自己的命题改编、磨题的基本功不足，又觉得这样的机会也不是很多，于是平时就放松对命题改编功夫的修炼与精进.事实上，命题功夫主要还是来源于教师日常教学、备课与作业设计上，因为备课过程中必然涉及对例、习题的改编呈现，而不是“照本宣科”“照讲义讲题”，这时就会深入理解习题的深层结构，习题考查或训练的重点，明辨难点，并有针对性地增设铺垫式问题或成果扩大式的解读.

2.考试命题考虑“时长”研判学情

考试命题不同于日常教学设计中的例、习题的变式改编，或者作业设计中的成果扩大式的改编与追问.因为考试是限时独立完成，不是课堂上可以有学生分组的讨论、全班交流研究、教师的适时和相机点拨，而且目前初中阶段的考试题量大、时间紧，有些所谓的好题（特别是占版面很大的研究性习题就不太适合选用），学生并不是解答不出来，很多情况下是因为前面的题量大、运算量大，到了最后的两道大题，绝大多数学生都没有时间去“看一眼”，这种试题安排在试卷上往往达不到诊评、区分或选拔的效果，是值得很多命题者反思的.