低处着手 高处点睛——以一道一次函数应用题为例看教学

（浙江省开化县村头初中；浙江省衢州市实验学校）

测试的目的是评价，评价的目的是改进教学，做到直击要害，精准教学.从测试结果中发现学生的“不会”，找到“不会”的根源并深化教学方式，才能实现更好、更深刻的“会”.浙江省衢州市2017—2018学年八年级上学期期末数学调研试卷第22题是一道一次函数的应用题（以下统称“调研卷题”），该题满分为8分（试卷总分为100分）.命题组预估该题难度系数为0.70.衢州市某一学生整体素质较高的学校，总评该题的难度系数为0.45，最好班级的难度系数为0.57，最低班级的难度系数为0.322 5，这与教师预期结果差距较大.

为什么会有这么大的差距？学生“不会”的原因是什么？如何改进教学才能达到“会”的目标？带着这些问题，我们进行了如下的分析和思考.

一、原题呈现

调研卷题小聪在学习时看到一则材料：甲、乙两人去某风景区游玩，约好在飞瀑见面.早上，甲乘景区巴士从古刹出发，沿景区公路去飞瀑（如图1）；同时，乙骑电动自行车从塔林出发，沿景区公路去飞瀑.设两人行驶的时间为t（h），两人之间相距的路程为s（km），s与t之间的函数关系如图2所示.小聪观察、思考后发现了如图2所示的部分正确信息：①两人出发1小时后第一次相遇；②线段CD表示甲到达飞瀑后，乙正在赶往飞瀑途中时s随t的变化情况，……试应用相关知识，与小聪一起解决下列问题.

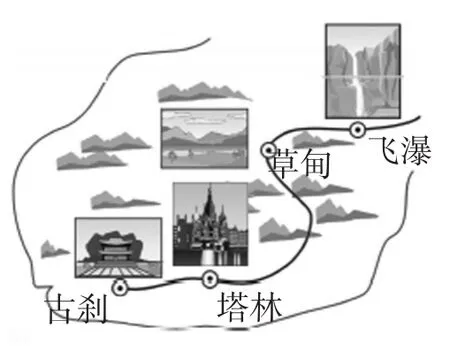
图1

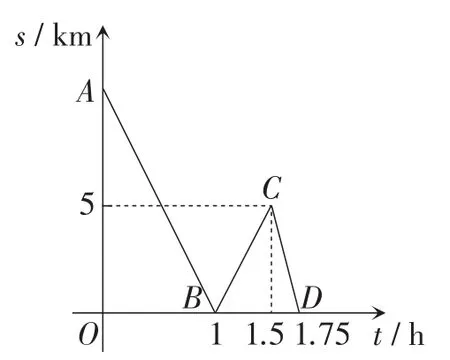
图2

（1）求乙骑电动自行车的速度.

（2）当甲、乙两人第一次相遇时，他们离飞瀑的距离还有多少？

（3）在行驶途中，当甲、乙两人之间相距的路程不超过1 km时，求t的取值范围.

二、追根溯源

1.以教材例题为本，取法教材

上述调研卷题取材于浙教版《义务教育教科书·数学》八年级上册“5.5一次函数的简单应用”中的例2.例2的具体内容如下.

小聪和小慧去某风景区游览，约好在飞瀑见面.上午7：00，小聪乘电动汽车从古刹出发，沿景区公路（如图3）去飞瀑，车速为30 km/h.小慧也于上午7：00从塔林出发，骑电动自行车沿景区公路去飞瀑，车速为20 km/h.

图3

（1）当小聪追上小慧时，他们是否已经过了草甸？

（2）当小聪到达飞瀑时，小慧离飞瀑的距离还有多少？

解：设经过t时，小聪与小慧离古刹的路程分别为s1，s2，由题意，得s1=30t，s2=20t+10.在直角坐标系中画出直线s1=30t和直线s2=20t+10（如图4）.

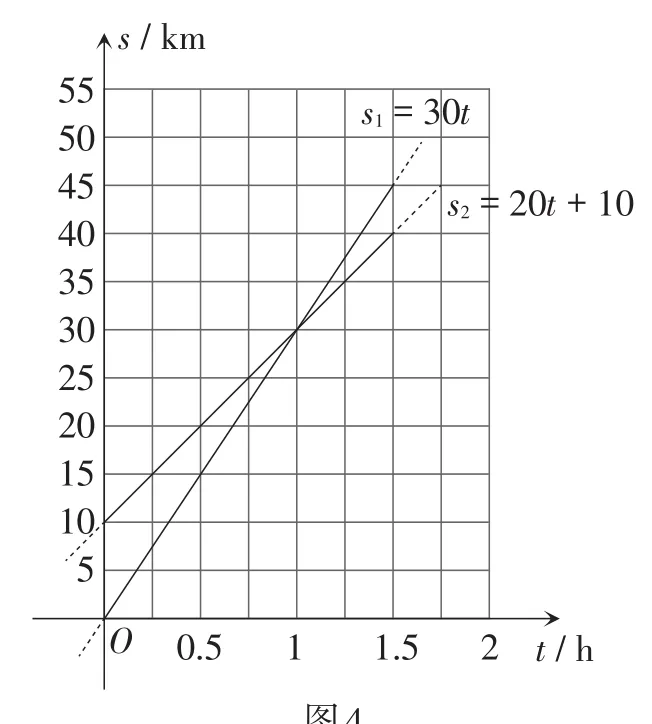
图4

（1）两条直线s1=30t，s2=20t+10的交点坐标为(1,30),所以当小聪追上小慧时，s1=s2=30 km，即离古刹30 km，小于35 km，也就是说，他们还没到草甸.

（2）如图4，当小聪到达飞瀑时，即s1=45 km，此时s2=40 km.所以小慧离飞瀑还有5 km.

以上教材解法突出了函数图象的性质及其应用.在学生还没有完全理解一次函数图象的本质，或者还依赖于列方程解应用题的情况下，对新知的陌生感会导致其接受和理解新知出现困难.

2.以中考试题为范，学法变式

上述调研卷题的命制也参考了2015年浙江金华中考试卷第22题，试题如下.

小慧和小聪沿图5中的景区公路游览.小慧乘坐车速为30 km/h的电动汽车，早上7：00从宾馆出发，游玩后中午12：00回到宾馆.小聪骑自行车从飞瀑出发前往宾馆，速度为20 km/h，途中遇见小慧时，小慧恰好游完一景点后乘车前往下一景点，上午10：00小聪到达宾馆.图6中的图象分别表示两人离宾馆的路程s（km）与时间t（h）的函数关系.

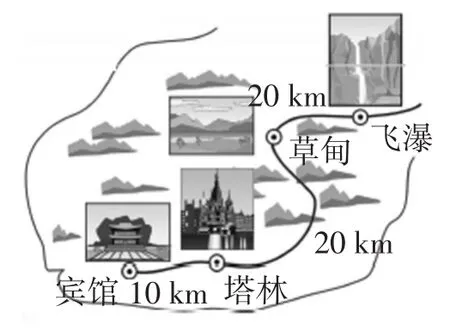
图5

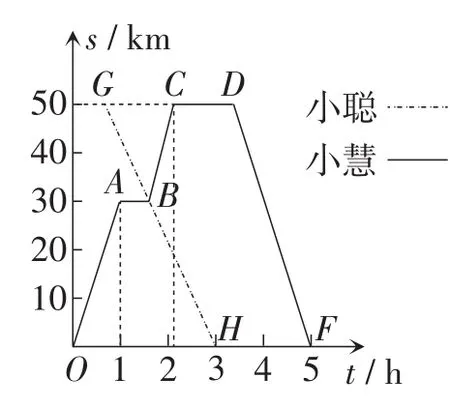
图6

试结合图中信息回答下列问题：

（1）小聪上午几点钟从飞瀑出发？

（2）试求线段AB，GH的交点B的坐标，并说明它的实际意义.

（3）小聪到达宾馆后，立即以30 km/h的速度按原路返回，那么返回途中他几点钟遇见小慧？

调研卷题将上述中考试题的第（1）小题中的求时间改为求速度.解决该中考试题第（2）（3）小题的重点在于深入理解图象交点的代数意义和几何意义，运用的基本方法有列式计算、待定系数法、解方程组等，解题难点是要依据图象获取信息.

3.以典型方法为纲，效仿运动

调研卷题的命制也参考了如下试题中的运动方法.

一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发.设慢车行驶的时间为x（h），两车之间的距离为y（km），图7中的折线表示y与x之间的函数关系.

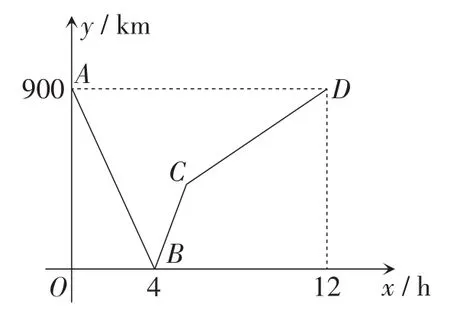
图7

根据图象进行以下探究.

（1）试解释图7中点B的实际意义，并求慢车和快车的速度.

（2）求线段BC所表示函数表达式，并写出自变量x的取值范围.

（3）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同.在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇.求第二列快车比第一列快车晚出发几个小时？

此题难在求得慢车速度为75 km/h，两车速度之和为225 km/h后，线段BC的函数表达式是y=225x-900(4 ≤x≤6).当慢车与第一列快车相遇30分钟后与第二列快车相遇时，慢车行驶了4.5 h，这时y=112.5，由于慢车与第一列快车之间的距离等于两列快车之间的距离为112.5 km，所以两列快车出发的间隔时间是0.75 h，即第二列快车比第一列快车晚出发0.75 h.

三、反思与建议

综观调研卷题，链接和整合了一次函数的一些碎片化知识、思想、方法、技能及活动经验，有较强的综合性.该校全体学生得分统计情况如下表所示.

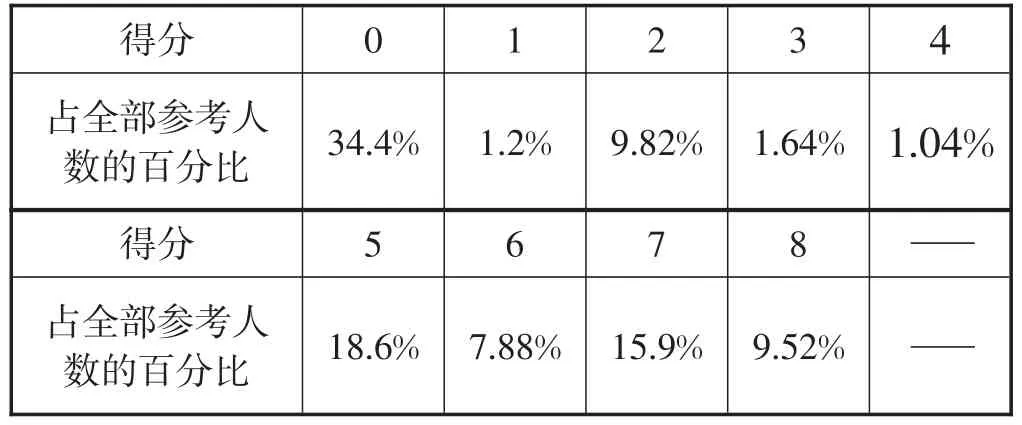
_______________________________________________________4 0______1______2______3得分__________________________________________占全部参考人__数的百分比________________________________________34.4%1.2%9.82%1.64%1.04%______________________5得分________________占全部参考人__数的百分比6______7______8__________18.6%7.88%15.9%9.52%

由上表可知，0分的学生超过参考人数的三分之一，说明没有理解题意或捕捉到文本信息的学生就占了三分之一；能依据图象所呈现的非连续性文本获取信息的学生可以求出电动自行车速度，得2分；能结合图象的实际意义和数学意义解决问题的学生，能完成第（2）小题，共得5分；有较强的分析能力和综合运用能力的学生能顺利找到第（3）小题的解答方法，若有失误，如只求解其中一段或不等号判定错误，得7分，完全考虑清楚的学生得满分8分.

考评后，经调查、收集，整理了学生“不会”调研卷题的原因.这些原因启发我们：教学要着眼于知识发生、发展和变化的全过程，要从低处着手、高处点睛.

1.数形结合要关注实际问题的切入

依据“二元一次方程y=kx+b→取它的一个解这一学习过程，远比“电影票上的几排几座→有序数对→确定位置”这一具体而又有生活体验的学习流程抽象得多、复杂得多.如果教与学只能是依葫芦画瓢，表面上本分地接受，而内心因认知冲突而产生的强烈抗拒，教与学的效果都将大打折扣.

这一现象说明在这一阶段有部分学生还属于“形数分离期”，他们脑海中还没有把二元一次方程y=kx+b与直线y=kx+b联系起来，要突破对一次函数简单应用问题的解答，就要从“图形与坐标”这一内容开始，稳扎稳打，步步推进，做到低处着手.

例如，在“平面直角坐标系”的教学中，以坐标这一数学语言描述班级学生的位置时，可以进行如下归纳：横坐标相同的学生的连线是平行于纵轴的，纵坐标相同的学生的连线是平行于横轴的，不平行于坐标轴的斜线的学生的纵坐标是随着横坐标的变化而变化的，这就归纳出一次函数的增、减性的本质.

2.让学生做到碎片化知识的链接

在一次函数的简单应用的问题中，识别k，b的意义是基本功.图4中，两条直线解析式中的k分别表示小聪和小慧的速度，b分别表示他们从出发点距离古刹的路程；图7中，AB段的直线解析式中的k表示两车速度之和，b表示两地之间的距离.教学时，教师应根据实际情境引导学生进行理解、讨论、交流、辨析，让学生知晓k，b在不同情境中的实际意义.

也可以在依据一次函数的图象归纳出性质“对于一次函数y=kx+b(k,b为常数,且k≠0), 当k＞0时，y随x的增大而增大；当k＜0时，y随x的增大而减小”时，引入典型实际问题，让学生分析k，b的实际意义，加深其对k，b的实际意义的理解.教学中，教师应该引导学生把这些割裂的、碎片化知识有效地链接起来，这样才能使学生由此及彼，举一反三.

为了做到碎片化知识的链接，教师可以采用专题研究、长短作业结合等形式.随着学生数学学习的不断深入，学习方法的不断丰富，新知识的不断融入，新的思想和方法也要及时补充，这样才能开启知识的慧眼，才能见证知识的发生、发展，才能培养学生的数学核心素养.

3.落实“点”的教学，才能落实“线”的教学

“一次函数的简单应用”一课的教学应以图象上的点为载体，建立起知识“线”和知识“体”，要实现由数（一次函数解析式）到形（函数图象）的转化.教师在引导学生理解函数图象上点的含义的基础上分析点的由来，将一次函数与二元一次方程联系起来，实现由方程的解，到函数的有序数对，到坐标，最后到点的转化，并从有限的点中归纳出函数图象的特征，实现高处点睛，即数学原理的一般化.

至此解决一次函数的简单应用问题的方法有列（算）式计算、列一元一次方程、列二元一次方程（或方程组）和列不等式.单一的讲授函数建模这一思想，不利于问题解决策略的相互融合，不利于学生对数学建模思想的理解和掌握，不利于学生利用模型解决问题能力的提升.因此，教与学应该在学生已有的方法上研习数学建模思想，这样才能更好地巩固拓展.

4.让学生在总结环节学会自主整合和创新

当单独的连续性文本信息被转换成“多合一”的非连续性文本信息后，有些直观的数量关系变得隐晦而难以被学生发掘.这种变化，增大了问题解决的难度.

授人以鱼，不如授人以渔.从教的本质来看，是要让学生具备数学核心素养.可见，让学生自我开悟的关键是在递进式的学习中学会自主整合、自主创新，以实现知识的融合、方法的归一、能力的万化，实现数学核心素养的落地.

2019年浙江省宁波市中考数学试卷第24题也取材于调研卷题这一素材.其实，无论试题如何变化，只要教师以学生的学习为中心组织教学，做好知识的碎片化链接，实现数学原理的一般化，学生答题就不会受囿于试题的某种形式.