惯性起爆弹丸内装药摩擦起爆特性

章猛华,张 成,阮文俊,王 健

(1.苏州工业职业技术学院 机电工程系,江苏 苏州 215100;2.南京理工大学 能源与动力工程学院,江苏 南京 210094;3.上海宇航系统工程研究所,上海 201109)

随着重型装甲、新型复合材料、轻型高强度防护材料的广泛运用,现代战场逐步走向多功能化。现代高科技战争对多功能弹药的性能提出了更高的要求。为满足未来战场的任务需求,迫切需要对传统多功能弹药进行性能改进并增强毁伤能力。因此,深入分析及研究多功能弹药的作用机理,可以很大程度地减小研制周期及成本。

受内部空间的限制,穿爆类小型弹药如果采用传统引信技术,会对引信技术提出很大挑战,同时也会大大增加生产成本。所以此类弹丸的起爆一般采用无引信结构,弹丸的起爆依靠的是惯性体的惯性作用力。惯性体既是点火元件又可以作为杀伤元件,因此,弹丸在击穿目标之后的适时释能是此类弹药有效毁伤的关键。传统穿甲爆炸燃烧子弹由于作用效果不佳,较难实现靶后释能[1]。美国ATK公司在21世纪初对穿爆类弹药进行技术改进,使弹药能更高效地完成预期毁伤效果[2]。为了对现有弹药进行优化,合理控制靶后释能,需要对弹丸内装药的点火起爆特性进行定量分析。弹丸在穿透靶板的过程中,惯性体在惯性力的作用下向前运动,刺入及挤压弹内装药,两者之间的摩擦作用是装药起爆的关键因素[3]。

惯性体对装药的作用压力和滑动速度是影响炸药摩擦温升的主要因素。由于弹丸的高速撞靶过程只能持续数十微秒,惯性体对内部装药的作用过程难于进行测量,无法对内部装药的起爆过程进行详细描述[4]。因此,数值模拟方法成为解决此类问题经济且高效的首要研究手段[5-7]。本文对弹丸撞击起爆过程进行试验研究,并基于炸药的热爆炸理论,建立装药摩擦起爆模型,结合非线性软件LS-DYNA,分析惯性体对装药接触面间强摩擦生成热点的温度上升特性。通过试验与数值计算的相互印证,验证模型的有效性。

1 试验研究

出于机理分析考虑,对弹丸结构进行适当简化,简化后结构如图1所示。弹头采用截锥形设计,锥度为40°,截锥直径为2.75 mm。弹头、壳体和底盖均为高强度钢。弹带用以保证发射过程内弹道数据的稳定,材料为紫铜。内部装药为钝化RDX,颗粒直径小于等于0.38 mm,装药密度均为1.65 g/cm3。惯性体采用双锥结构设计,头锥为90°,二锥为20°,直径为7 mm,长度为36 mm,惯性体材料为高强度钢。导向套用以保证惯性体的平稳运动,材料为2024铝。

图1 弹丸平面结构

弹丸由14.5 mm的弹道枪发射,高速摄像机(Fastcam Mini UX50)由弹丸穿过第一个锡纸靶后触发并开始采集,由于穿靶时间及炸药爆炸时间较短,所以在能够满足观测的情况下,尽量提高高速录像的拍摄频率,本次试验的拍摄频率为40 000 s-1,确保能够获取较为精确的起爆时间数据。试验中的目标钢靶材料为Q235,由于需要根据调整靶板厚度来确定弹丸的撞击起爆条件,所以准备的靶板厚度为4～8 mm。

图2 弹丸及其构件实物

图3 场地布置

通过升降法(改变弹丸的着靶速度v0及靶板厚度δ)来确定弹丸的撞击起爆阈值条件,根据高速摄像记录的数据及目标靶板的毁伤情况来确定弹丸起爆与否。试验筛选出5发有效数据,如表1所示,表中,m表示弹丸质量。

表1 撞击起爆试验数据

对起爆的试验进行高速录像分析,第4发试验未获得高速录像数据,第3发及第5发高速录像数据如图4和图5所示。从图中可以看出,第3发弹丸的起爆时间为125～150 μs,第5发弹丸在着靶后75～100 μs起爆,2发弹丸起爆后都伴有强烈的火光,且持续几毫秒。由于第5发的钢靶的厚度更大,所以弹丸的起爆时间较早,从撞靶500 μs时爆炸火球中心与靶面的距离也能看出,后者的火光位置距离靶板更远。

图4 第3发试验撞击起爆过程

图5 第5发试验撞击起爆过程

2 摩擦起爆计算

2.1 温升模型

在穿甲过程中,弹丸的尖形惯性体在惯性力的作用下与装药产生相对滑移,界面间相互摩擦产生热量,热量同时向炸药及惯性体内部传导,炸药及惯性体温度随之升高。弹丸穿甲的过程一般为微秒量级,因而摩擦加热的时间也是微秒量级。因此,热传导引起的装药温度升高区域很薄,可以近似看作为薄板型热点。

在一定时间内,热能够传输的距离被称为热扩散距离L,其特征尺寸为[8-9]

(1)

式中:α为热扩散率,α=λ/(ρcp),λ为导热率,ρ为密度,cp为比定压热容;t为摩擦加热特征时间。

由于摩擦加热特征时间为微秒量级,因此炸药热层的加热尺寸为微米量级,此特征尺寸远小于装药半径,可以把问题简化成一维平面传热。炸药采用一维热反应扩散方程,厚度方向为x方向,则

(2)

式中:下标1表示炸药,T1为炸药薄层温度,Q1为传入炸药的摩擦热。

惯性体热传导方程为

(3)

式中:下标2表示惯性体。

炸药与惯性体摩擦产生的热量为摩擦力做的总功,Q=μpΔv,其中p是惯性体与炸药中的压力,μ是动摩擦系数,Δv是惯性体与炸药之间的相对速度。如果不考虑其他能量损失,认为摩擦产生热全部传入了惯性体和炸药,则Q=Q1+Q2。

(4)

求解这个方程组的关键在于求解炸药和弹芯边界的Q。因此,要得到炸药薄层内的温度分布,首先要确定弹芯与装药之间的相对滑动速度和弹芯对装药的最大压力,而这个作用过程较为复杂,因此,采用非线性动力学分析软件LS-DYNA对弹丸侵彻靶板过程进行数值分析,获取弹芯与装药之间的相对滑动速度和表面压力曲线。

2.2 穿靶过程数值模型

对模型进行简化,并建立1/4模型,简化后的模型如图6所示。考虑到炸药材料的特殊性,采用SPH方法模拟的结果更为准确[11],因此,对炸药进行SPH建模,对其他部分进行有限元网格划分,图7为弹丸数值模型。

图6 简化后的弹丸结构

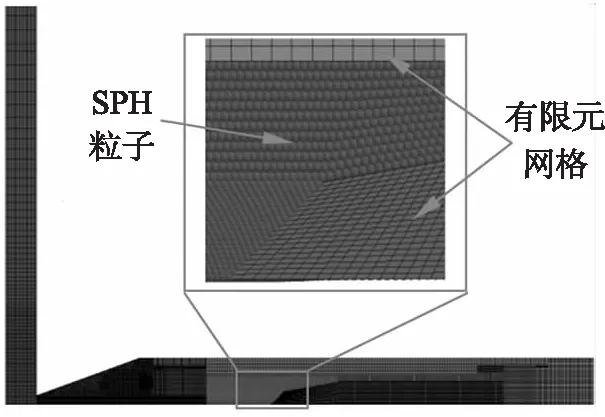
图7 弹丸数值模型

分别对400 m/s,600 m/s,800 m/s速度时弹丸撞击4 mm靶板的情况进行模拟。装药所受压力云图如图8所示,从图中可以看出,压力最大的区域出现在与惯性体头锥接触的部位,所以这个区域是装药的点火起爆区域。3种情况下装药表面的压力如图9所示,由图可知,撞击速度越大,应力波的传播速度越快,惯性体对装药的惯性作用时刻越靠前,压力曲线上升时间越早。但是,撞击速度越大,装药表面压力持续时间越短,最大压力越小。这是由于随着撞击速度增加,弹丸穿透靶板所用时间越短,所以惯性体对装药的作用时间越短,压力成长时间越短,最大压力也越小。因此,在其他条件都相同的情况下,撞击速度越大,惯性作用时间越短,装药所受总冲量越小,装药越不容易起爆。

图8 炸药所受压力云图

图9 不同速度时炸药表面压力曲线

因此,相对于第1发573 m/s的撞击速度,第2发402 m/s的撞击速度更接近临界起爆条件。根据实验结果,弹丸穿透靶板未起爆的最大撞击条件为,以402 m/s速度撞击4 mm靶板(以下简称工况1);装药被起爆的最小撞击条件为,以565 m/s的速度撞击4.75 mm厚的靶板(以下简称工况2)。所以,可以确定弹丸的点火阈值在这2种工况之间。对2种工况下的穿靶过程进行模拟,得到2种工况下的表面最大压力曲线,如图10所示。从图中可以看出,弹丸在侵彻靶板时,由于工况2时弹丸的速度较高,应力波的传播速度较快,惯性作用时间也相对较靠前,所以压力上升时刻较早。由于靶板变厚了,所以2种工况下装药所受惯性力的结束时间相差不大。但是工况2的最大压力高于工况1,所以炸药所受冲量也越大,印证了试验中工况2爆而工况1未爆的结果。同样,也可以得到2种工况下惯性体与装药之间的相对速度,如图11所示。

图10 2种工况炸药表面的压力曲线

图11 2种工况炸药与惯性体相对速度曲线

2.3 温升计算结果及分析

根据前文建立的摩擦起爆模型,对装药的摩擦起爆过程进行计算,计算过程中炸药及惯性体的材料参数见表2[12-13]。计算过程中先假定一个动摩擦系数μ,对工况2的摩擦温升进行求解。如果不发生起爆,则增大摩擦系数重新计算;如果发生爆炸,则减小摩擦系数,直到找到发生爆炸的最小μ值。最终得到的炸药与惯性体的动摩擦系数为0.04。

表2 炸药及惯性体材料参数

图12为2种工况下炸药温度变化曲线。从图中可以看出,工况1炸药未起爆,最高温度为560 K,出现在92 μs。此后,由于炸药与惯性体的相对速度降为0,炸药反应放热量小于热传导的耗散量,失去摩擦热的作用,炸药温度将持续下降,最终降为0,炸药未起爆。工况2中炸药温度在105 μs产生拐点,说明此时炸药的反应热已经超过热传导所散失的热量,达到了起爆的临界条件,在120 μs左右温度开始急剧上升,炸药发生起爆。

图12 2种工况炸药温度变化曲线

从工况2模拟的穿靶情况可以知道,在撞靶120 μs时,装药段已经穿过靶板,如图13所示。所以此时爆炸发生在靶后,试验得到的起爆时间在125～150 μs。由于本文只针对炸药的起爆阶段进行分析,并没有考虑装药在点火起爆后的增长过程,炸药的实际起爆时间应该略晚于计算得到的炸药起爆时间。同时高速读取存在一定的误差,造成计算结果与试验结果存在一定误差。但是总体而言,起爆时间的数值模拟结果与试验观测值符合较好。

图13 弹丸撞靶120 μs时的状态

为进一步验证计算结果,对第5发试验(工况3)起爆时间进行计算分析,通过计算,得到装药的温升曲线,如图14所示。从图中可以看出,在67 μs时装药温度开始急剧上升,此时热点开始向外扩散,装药被点火,70 μs后实现起爆。试验得到的起爆时间为75～100 μs,模拟结果与之吻合较好。

图14 工况3炸药温升曲线

3 结论

①在弹丸能够有效穿透靶板的情况下,弹丸着靶速度越低,弹丸穿透靶板的时间越长,惯性体对装药的作用时间也越长,装药所受总冲量越大,越容易起爆。

②弹丸的最低起爆条件是以576 m/s的速度撞击4.75 mm的钢靶,最高不起爆条件是以410 m/s的速度撞击4 mm钢靶。通过摩擦起爆计算,得到钝化RDX与惯性体之间的动摩擦系数为0.04。

③采用计算拟合得到的摩擦系数对工况3的起爆时间进行计算,得到装药的起爆时间为70 μs,与试验得到的起爆时间75～100 μs吻合较好。