炸药底隙对炸药装药发射安全性的影响

严 涵,于艳春,芮筱亭,陈卫东

(1.哈尔滨工程大学 航天与建筑工程系,黑龙江 哈尔滨 150001;2.东北农业大学 水利与土木工程学院,黑龙江 哈尔滨 150030;3.南京理工大学 发射动力研究所,江苏 南京 210094)

随着高膛压火炮的发展,炸药装药在发射过程中的冲击过载增大,容易使炸药在发射状态下发生膛炸。因此,炸药的发射安全性问题具有重要的研究价值[1-4]。国内外大量的实验结果和理论研究成果得出较为一致的结论,即底隙是导致炸药装药发生膛炸的主要因素。底隙中的残留空气受到膛内高压载荷的作用,使空气被压缩,炸药底部形成高温热点,同时会加热相邻的炸药层。底隙中残留空气受压缩程度越大,炸药底部的热点温度越高,引起炸药早炸和膛炸的几率越高。

美陆军弹道研究所采用BRL激励器实验研究装置,进行了多年的模拟实验研究,发现底隙是引起炸药装药在发射环境下膛炸的主要因素[5]。在国内,很多学者开展了底隙对发射安全性影响的研究工作。肖作智等[6]进行了B炸药试样的水试验,试验结果表明,底隙能够引起炸药膛炸。李文彬等[7]采用有限元的方法模拟了当底隙存在时炸药在发射过程中的应力分布,研究了不同时刻、不同底隙厚度对炸药应力分布的影响。张涛等[8]研究了不同装药工艺对炸药安定性的影响,分析了影响炸药安定性的原因。李瑞静[9]研究了炸药缺陷对炸药性能的影响。王豪[10]对炸药装药的发射安全性计算进行了研究。虽然学者们在相关领域做了大量的研究工作,但定量分析炸药底隙对炸药安全性影响的相关文献相对较少。

广义黏弹性统计裂纹本构模型描述了微裂纹的扩展机制,将裂纹体与广义黏弹性体耦合在一起,描述炸药的黏弹性力学性能及其损伤过程,更加真实地反映了炸药的力学特性。有限体积法是一种被广泛应用于计算流体力学领域的数值方法,近些年,该方法在固体力学领域也得到了较好的发展。由于有限体积法采用时域的显式积分算法,因此特别适用于求解爆炸、冲击等高度非线性问题。因此,本文基于广义黏弹性统计裂纹本构模型,采用有限体积法研究了炸药在压力载荷的作用下,底隙对炸药发射安全性的影响,定量地分析了底隙中残留空气的压缩量对炸药内部应力、温度及点火情况的影响。

1 有限体积法

本文采用显式的有限体积法开展炸药发射安全性研究。显式算法是基于动力学方程,无需迭代,计算速度快,所需内存少,容易收敛;数值计算过程容易实现并行计算,程序编制简单,且具有较好的稳定性,尤其适用于求解高速动力学问题,诸如冲击、爆炸和碰撞等高度非线性问题。

与有限元法类似,首先需要对求解域进行离散,形成有限体积法的控制体积。由于显式积分算法基于动力学方程,所以有限体积法的离散过程是将动力学方程在控制体积内积分,最终建立离散方程。

如图1所示的控制体积V,由3-4-5-6-7-8-9-10-11-12共同围成,D为该控制体积的中心。

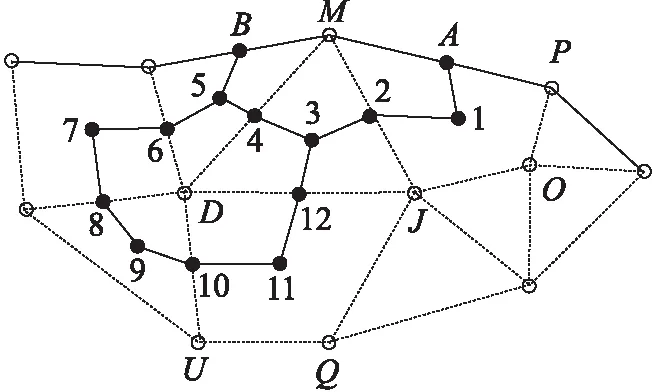
图1 控制体积的示意图

将动力学方程在控制体积内积分,得:

(1)

(2)

式中:Fi为力Fs在3个轴的分量;σil为应力张量;nl(l=1,2,3)为单元表面S的外法线向量n的分量,对于平面问题,方程(1)可简写为

(3)

式中:nj(j=1,2)为曲线的外法线向量的分量。二维平面问题的平衡方程在控制体积内的积分为

(4)

(5)

由于σxx,σyy和σxy在线性插值三角形单元里是常数。假设应变在划分的网格单元内是常数,且其值设置在单元的中心点。通过以上的假设,如图1所示,由M-1-2-3-4-5-B所围成的控制体积,控制体积的中心为M,通过集中质量法进行离散化[11],详细推导过程参见文献[11],最终的离散方程可以写为

(6)

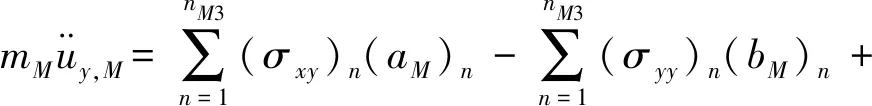
(7)

2 广义黏弹性统计裂纹模型

本文中炸药的本构模型采用的是广义黏弹性统计裂纹本构模型。广义黏弹性统计裂纹本构模型适用于碰撞、爆炸和冲击等问题的研究。炸药本构模型的具体推导过程见文献[12-14],这里只给出简要的计算公式。

(8)

(9)

式中:G(q)为第q个弹性元的剪切模量。

Dienes等[14]在研究工作中描述了裂纹的增长速率,假设裂纹的增长速率与应力强度有关,即

(10)

式中:

(11)

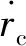
3 宏观体积加热模型

本文采用宏观体积加热模型描述炸药温度变化的模型。在计算时,对于整体的热量变化,可以忽略宏观体积加热模型的热传导项,该模型的具体表达式为

(12)

式(12)右边第一项为绝热压缩项,其中,T代表温度,γ为Gruneisen系数,εii为应变率;第二项为由黏性效应和裂纹损伤引起的非弹性功率;其中,Pve为黏性功率,Pcr为裂纹损伤功率:

(13)

(14)

式(12)右边第三项代表整体化学热,其中,cV为比定容热容,取值为1 200 J·kg-1·K-1,ΔQ为炸药热分解反应单位质量的分解热,取值为5.5×106J/kg,EA为炸药热分解反应单位质量的活化能,EA/R取值为2.652×104K,Z为炸药热分解反应单位质量的指前因子,取值为5×1019s-1,ρ为密度,取值为1 810 kg/m3。

式(12)除了温度以外的所有变量都可以通过黏弹性统计裂纹模型求出,因此,该式可以看成是关于温度T的常微分方程,对时间进行积分即可得到一个单元的温度状态。

4 状态方程

一般来说,状态方程是用来描述材料的压力、体积与温度之间的关系。炸药在外界刺激下的压力采用状态方程进行更新。研究不同的材料一般采用不同的状态方程。本文计算采用固态JWL状态方程描述炸药压力的更新状态,其表达式如下:

(15)

式中:p为压力;E为单位初始体积内能;V*为相对体积;A1,B1,R1,R2,w代表材料参数[15],取A1=77.81 kPa,B1=-5.031 Pa,R1=11.3,R2=1.13,w=0.893 8。

5 数值计算

采用有限体积法,利用黏弹性统计裂纹本构模型并结合JWL状态方程自编程序计算了炸药底隙在压力作用下,炸药内部的应力及温度的变化,分析了底隙中残留空气压缩量与炸药底部温升的关系,讨论了底隙中残留空气压缩量对炸药点火状态的影响。炸药的计算模型如图2所示。

图2 计算模型

炸药模型尺寸总长556 mm,最大半径62 mm。数值模拟的材料采用PBX9501炸药。由于广义黏弹性统计裂纹模型中的参数很多,但目前的研究论文中仅给出了PBX9501炸药的相关参数。下面分别给出了PBX9501炸药的统计裂纹参数、松弛参数、黏弹性体的参数[12-13]。

统计裂纹参数:r0为裂纹初始半径,取r0=0.03 mm,m=10,vmax=300 m/s,a=0.001 m,K0=5 kPa·m1/2。

松弛参数:1/τ(1)=0,1/τ(2)=7.32×103,1/τ(3)=7.32×104,1/τ(4)=7.32×105,1/τ(5)=2.00×106。

黏弹性体参数:G(1)=944.0 MPa,G(2)=173.8 MPa,G(3)=521.2 MPa,G(4)=908.5 MPa,G(5)=687.5 MPa。

在模拟炸药应力及温度变化的过程中,在炸药底部施加压力载荷,其压力曲线如图3所示。

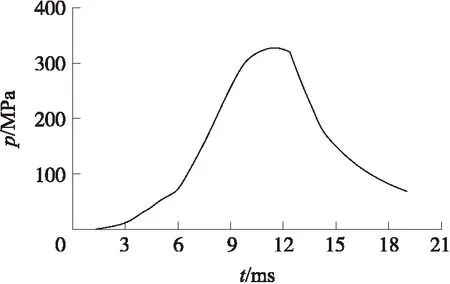
图3 压力载荷曲线

采用有限体积法计算了在压力作用下,考虑炸药底隙时炸药内部温度和应力的变化规律。计算时,首先,讨论随着炸药底部温度的变化,炸药内部的应力和温度的变化趋势及炸药的点火情况;然后,分析炸药底隙中空气的压缩量与炸药底部温升之间的关系;最后,结合以上两方面的讨论,分析炸药底隙的厚度对炸药内部应力和温度的影响。

首先,讨论炸药底部不同的初始温度对炸药内部温度和应力的影响。假设炸药内部的初始温度为300 K,当炸药底部初始温度分别为400 K,450 K,500 K,而炸药内部其他部位初始温度仍为300 K时,绘制了炸药底部C(55.6,3.1)(cm)点位置处温度和应力的时程分布曲线，同时给出了不同时刻炸药内部的温度和压力云图，计算结果如图4～图6所示。

①当炸药底部初始温度为400 K,其他部位初始温度仍为300 K时，计算炸药底部C点位置处温度和应力的变化曲线及不同时刻炸药内部压力和温度的变化云图,如图4所示。

②当炸药底部初始温度为450 K,其他部位初始温度仍为300 K时，计算炸药底部C点位置处温度和应力的变化曲线及不同时刻炸药内部压力和温度的变化云图,如图5所示。

③当炸药底部初始温度为500 K,其他部位初始温度仍为300 K时，计算炸药底部C点位置处温度和应力的变化曲线及不同时刻炸药内部压力和温度的变化云图,如图6所示。

图4～图6中,X,Y分别为炸药模型在x方向和y方向坐标尺寸。

从以上计算结果可以看出,在压力的作用下,炸药底部的应力变化趋势基本上与施加的压力曲线趋势是一致的,说明计算结果是正确的,本文提出的计算方法是可行的。当炸药底部的初始温度为400 K,其他部位温度为300 K,加载时间为18 ms时,计算得到的炸药底部的温度升高为505 K;当炸药底部的初始温度为450 K,其他部位温度为300 K,加载时间不变,计算得到的炸药底部的温度升高为570 K;当炸药底部的初始温度为500 K,其他部位温度为300 K时,加载时间不变,得到的计算结果是,当计算到14.7 ms时,炸药底部的温度已经达到了预设的点火温度,温度突然急剧升高,此时炸药发生了点火反应。以上计算结果说明,在底部压力的作用下,炸药底部温度会升高,当温度升高至500 K时,容易引发炸药点火。

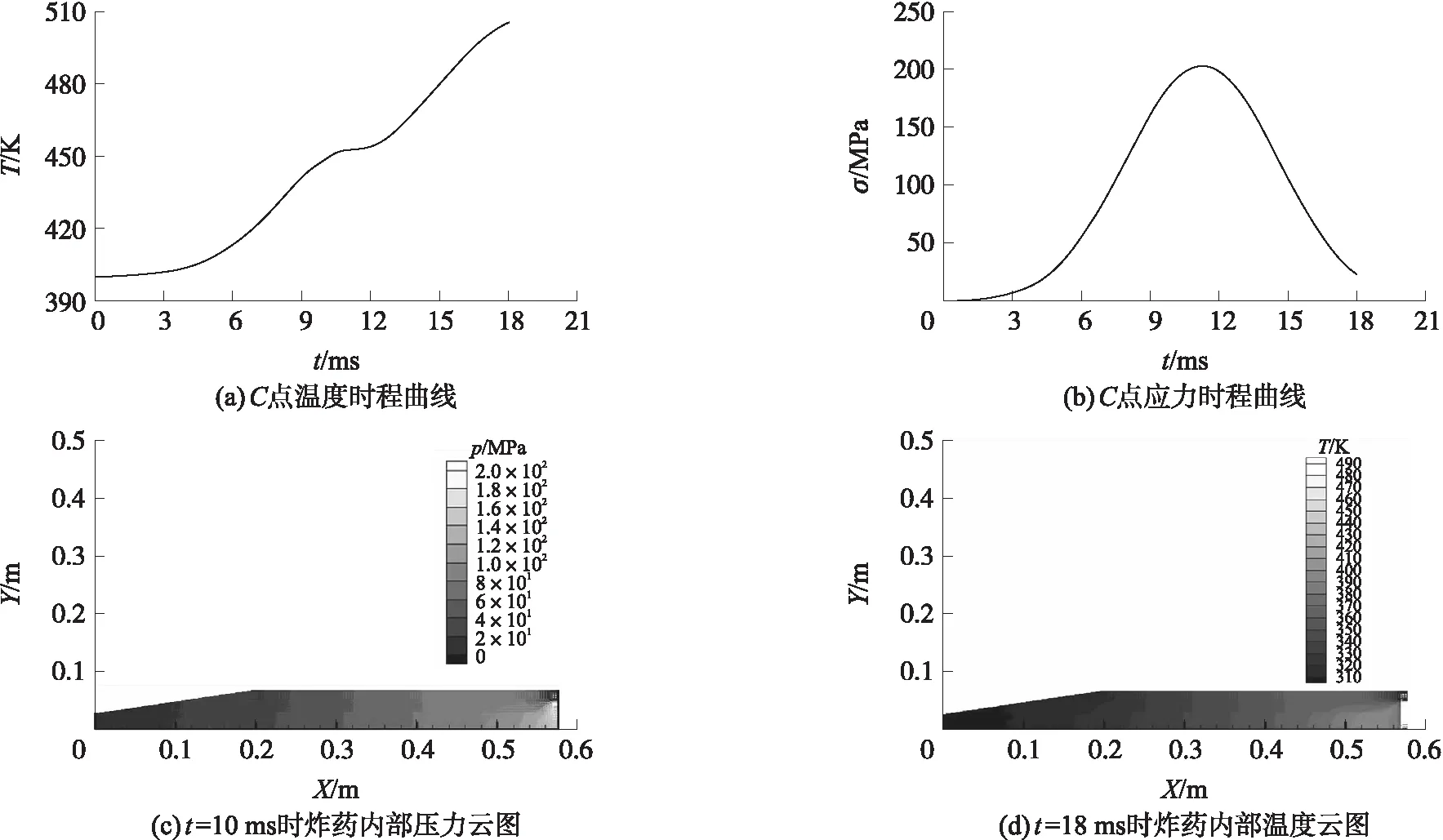
图4 初始温度为400 K的时程曲线和云图

图5 初始温度为450 K的时程曲线和云图

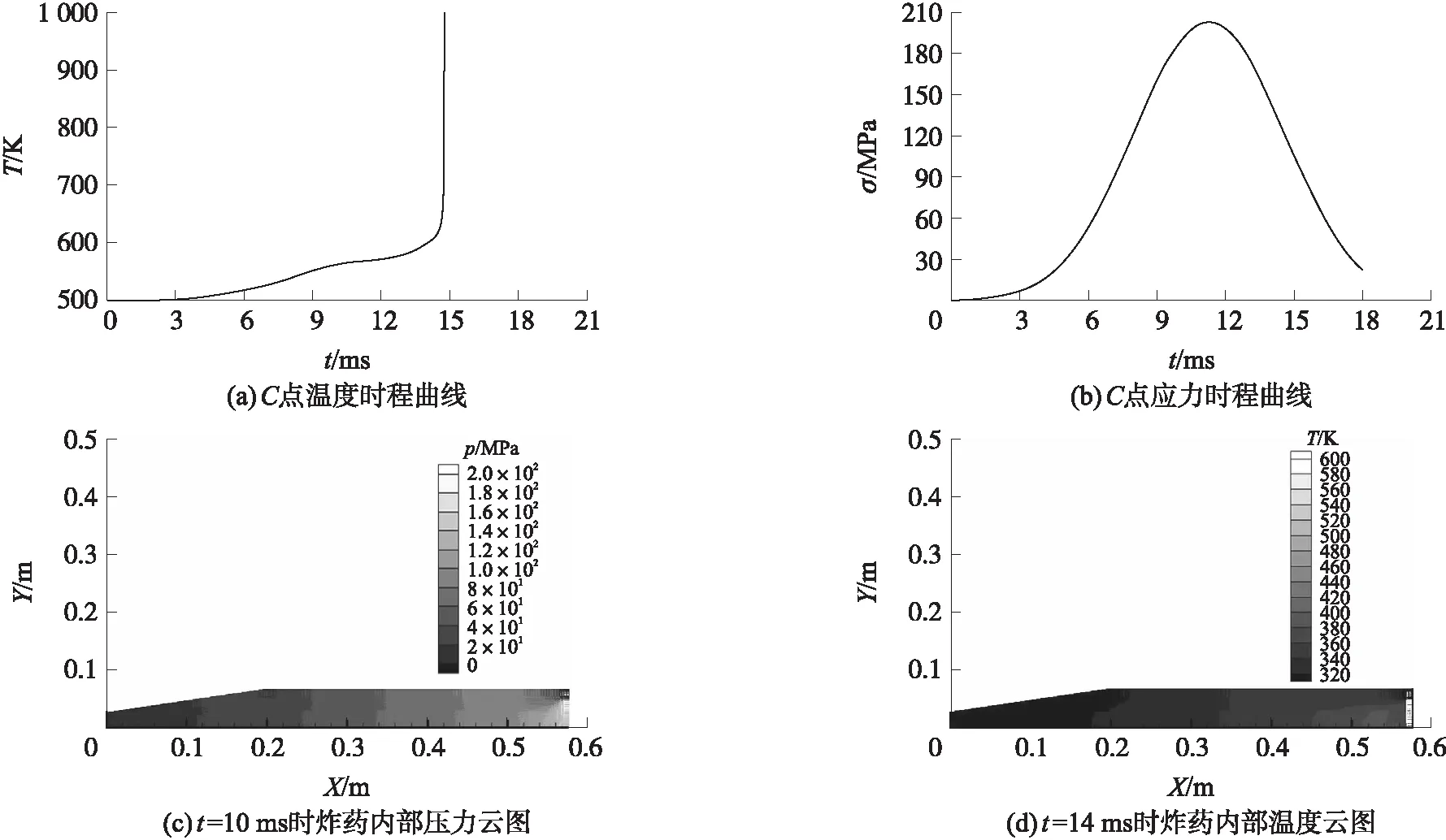
图6 初始温度为500 K的时程曲线和云图

其次,研究炸药底隙中的空气压缩量与炸药底部温升之间的关系。底隙中留存的空气受到模拟的弹底压力作用,迅速压缩、加热相邻的炸药层,使炸药底部的温度升高,从而容易引发点火。由于底隙中的空气被很快地压缩,假设气体与外界来不及热量交换,可以把这个过程近似认为是气体绝热压缩过程,这样通过计算可以得出炸药-空气界面间的温度。

(16)

式中:T1,V1分别为压缩前理想气体的温度和体积;T2,V2分别为压缩后理想气体的温度和体积;γ为比热比,理想气体γ=1.4。

由式(16)可知,气体间隙绝热压缩后的温度只与气体的压缩比有关。如果保持压缩后的体积不变,则初始体积越大(底隙厚度越大),压缩比越大,压缩后的温度越高。本文算例考虑炸药底隙的影响,在模拟的弹底压力作用下,炸药底隙中的空气会被压缩。设炸药初始温度为300 K,当底隙中的空气被压缩33%时,根据理想气体绝热压缩状态方程可知,炸药底部的温度由初始的300 K升高到354 K;当底隙中的空气被压缩50%时,炸药底部的温度升高到396 K;当底隙中的空气被压缩66%时,炸药底部的温度升高到465 K;当底隙中的空气被压缩75%时,炸药底部的温度升高到510 K。根据上面的分析可知,此时炸药发生了点火反应,这也说明了当炸药底隙中的空气被压缩超过75%时,炸药最终会发生点火反应。底隙中空气压缩量η与炸药底部温度升高间的关系如图7所示。这一结果与文献[7]中得到的结论是相吻合的,从不同侧面反映出底隙严重影响装药的发射安全性。

6 结论

本文采用有限体积法,利用黏弹性统计裂纹本构模型并结合JWL状态方程,定量分析了炸药底隙对炸药发射安全性的影响,得到以下结论:

①炸药在施加的压力载荷作用下,其内部的应力变化趋势与施加的压力载荷曲线变化趋势基本一致,说明本文提出的计算方法是正确的。

②定量地分析了炸药底隙的压缩量对炸药底部温升的影响。底隙中留存的空气受到压力作用,迅速压缩、加热相邻的炸药层,会使炸药底部的温度升高。依据理想气体绝热压缩状态方程,定量计算了当炸药底隙中的空气被压缩超过75%时,炸药底部的温度能够升高至510 K,容易使炸药达到点火温度。

③讨论了炸药底部不同初始温度对炸药内部温升的影响。当炸药底部(即炸药底隙处)的初始温度分别为400 K,450 K,500 K时,讨论了炸药在压力作用下的点火状态。当炸药底部的初始温度为500 K,其他部位温度为300 K时,加载时间不变,得到的计算结果是,当计算时间为14.7 ms时,其温度变化曲线突然急剧升高,温度值无限增大,说明炸药底部的温度已经达到了点火温度,发生了点火反应。