空间信息网络中面向双卫星的频谱共享方法
王闯,胡婧,李永强,边东明,李颂
中国人民解放军陆军工程大学 通信工程学院,南京 210007
空间信息网络包括卫星、升空平台、传感器、地面终端等各类节点,具备信息获取、传输、处理、分发和存储的能力,呈现立体多层、动态异构、资源受限、功能融合、多频共存的系统特点[1-4]。随着空间信息网络的迅速发展和人类空间探索范围的大幅提升,空间信息基础设施建设不断完善,越来越多的人造卫星和航空器被布置到太空,由此带来的频率资源紧缺的问题日益突出,传统的、静态的、单一的频率分配方式难以满足日益增长的服务需求。动态的频谱共享技术为空间信息网络寻找可用的频谱资源提供了思路,也是维持其高效、可靠、稳定运行的保障。因此,亟需针对空间信息网络的特点,开展空间信息网络频谱共享理论与方法的研究,为空间信息网络的建设提供频谱资源战略储备,提升中国在空间领域的综合信息服务能力。
1999年,“软件无线电之父”Mitola首次提出了认知无线电的概念[5],2005年,Haykin从信号处理的角度对认知无线电进行了全面的阐述[6]。认知无线电技术最典型的应用就是频谱共享,为缓解频谱资源紧张与实际利用率低下之间的矛盾提供了有效的解决途径,在物联网[7]、地面蜂窝移动网[8]、WiMAX[9]、航空通信[10]、无线自组网[11]以及卫星网络[12]等应用中发挥了重要作用。尽管现有的研究主要集中在地面系统,随着卫星网络与地面网络融合程度和资源共享水平的不断提高,对于卫星系统间的频谱共享也在深入探索中。相较于地面网络,认知无线电在卫星网络中的应用面临着卫星系统固有特性带来的一系列挑战,包括:长路径、大损耗、长时延、大覆盖、功放非线性以及长周期的系统研发制造带来的技术更新不及时等问题[13]。
认知卫星网络一般可分为星地混合认知网络和双卫星认知网络,其中星地混合认知网络是指在卫星和地面系统之间实现频谱共享,卫星系统可作为主用户(Primary User, PU),地面系统作为次级用户(Secondary User, SU)[14-16],同样,卫星系统也可作为SU,地面系统则为PU[17-20]。双卫星认知网络是指两个卫星系统共用一个频率对同一覆盖区进行服务,目前针对双静止轨道(Geostationary Earth Orbit, GEO)卫星系统的研究较多[21-24]。对于非静止轨道(Non-GeoStationary Orbit, NGSO)卫星,由于其相对地面高速移动,使得卫星系统间的干扰随着节点的空时行为而变化,尤其当GEO卫星、NGSO卫星和地面站三者共线,会产生严重的共视干扰(In-line Interference),使得系统的传输性能急剧下降甚至瘫痪[13]。
低轨道(Low Earth Orbit, LEO)卫星作为一种典型的NGSO卫星,在空间信息网络中发挥着重要的作用,尤其近年来由数百乃至上千颗LEO卫星组成的大规模星座系统,如SpaceX和OneWeb[25],引领着未来卫星发展的趋势。因而开展GEO和LEO卫星系统之间的频谱共享研究显得愈发重要。为应对GEO和LEO卫星系统之间存在的共视干扰,OneWeb系统引入了一种新型的“渐进倾斜”技术,在卫星接近赤道时通过逐渐地倾斜卫星来避免与GEO系统之间的干扰[26]。然而,调整卫星姿态需要消耗燃料,会引起卫星在轨寿命的缩短。文献[27]提出了一种自适应功率控制(Adaptive Power Control,APC)技术,通过对SU发射功率的自适应控制来保证PU的正常工作,从而实现GEO和NGSO卫星之间的频谱共享。此外,文献[28]提出了一种基于APC和跳波束技术的认知宽带卫星网络,关于APC的功率调整速率在文献[29]中做了进一步分析。可见APC技术是不同轨道卫星系统在进行频谱共享时常用的技术。但是,在采用APC技术时,为确保PU的正常工作,需要牺牲SU的性能,不可避免地造成SU频谱效率的下降。
本文针对空间信息网络中的GEO和LEO的双卫星系统共存的场景,提出了一种基于频率动态分配的新型频谱共享方法,在保护主用户的同时,次用户的性能也能够得到有效提升。具体而言,GEO系统作为PU,卫星采用多波束天线,采用七色频率复用,LEO系统为SU,卫星同样采用多波束天线。由于GEO卫星和LEO卫星的轨道高度差别较大,其对应的波束尺寸也相差较大,可在GEO波束中实现LEO波束的频率复用。通过分析GEO和LEO卫星同频波束间的距离与干扰之间的关系,提出了“隔离区域”的理念来实现频谱共享。在LEO卫星的运行过程中,当LEO波束接近GEO同频波束的隔离区域时,该LEO波束的频率会被重新分配以避免干扰。由于LEO卫星自身的波束之间也进行频率复用,因而一个波束频率的变化必然会引起一连串波束的频率变化,对此提出了一种频率动态分配算法,能够在提高网络容量的同时,明显降低卫星运动期间波束频率的切换频次。
1 双卫星频谱共享架构
如图1所示,在空间信息网络中,作为主用户的GEO卫星系统和作为次级用户的LEO卫星系统的下行链路共用同一频段,为用户提供宽带固定业务。两个卫星系统都采用多波束有效载荷,以频率的空间复用来提高频谱资源的利用率[30]。GEO卫星的频率复用因子定为7[31],图中每个GEO波束的频率各不相同。设定两个卫星系统的信关站由高速无损光纤连接,实时共享卫星星历、频率配置方案以及天线方向图,以此实现认知。在固定业务中,设定GEO和LEO用户的天线一直指向各自的卫星。
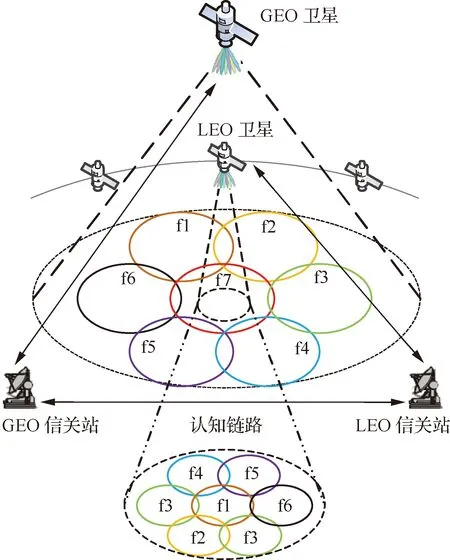
图1 LEO卫星和GEO卫星频谱共享的示意图Fig.1 Illustration of spectrum sharing between LEO and GEO satelites
由于卫星高度相差数十倍,GEO波束比LEO波束大得多。位于GEO波束内的LEO波束可以使用除所在GEO波束的其他任何频率,从而LEO卫星可以实现多波束的空分频率复用,但其频率复用因子必然小于GEO的频率复用因子。如图1所示,当LEO卫星运行到GEO卫星f7频率的波束内时,LEO波束使用的频率是f1~f6。考虑到LEO卫星相对地面运动,所以GEO和LEO波束之间的相对位置关系是动态的,当GEO和LEO的同频波束相距较近或重叠时,会引起同频干扰。由于LEO和GEO系统的信关站是互联的,根据共享的LEO卫星星历,包括轨道半长轴、偏心率、轨道倾角、升交点赤经、近地点幅角以及过近地点时刻等轨道参数,可以计算获得LEO卫星在地心地固(Earth-Centered Earth-Fixed,ECEF)坐标系中的位置矢量坐标和速度矢量坐标[32],在此基础上进一步得到波束的指向矢量和波束中心点的位置坐标。由于GEO卫星相对地面静止,其波束也是固定的。以GEO和LEO波束中心点之间的距离作为两个波束之间的距离,通过对卫星所有波束的计算,可以实时获得LEO和GEO卫星所有同频波束之间的距离。在初始化阶段,对LEO波束的频率进行预分配,该频率分配方案暂时保持不变。随着LEO的运动,当LEO卫星中存在某个波束与GEO同频波束的距离即将小于安全隔离距离时,LEO卫星的波束频率方案要进行重新分配以避免干扰。分配后维持该频率方案不变直到再次出现同频波束距离小于安全隔离距离的情况,以此往复,在LEO卫星的运动过程中根据星历和频率信息进行预测,适时地重新分配LEO波束的频率。可以知道,精细设计的频率分配方案可以有效地避免干扰,而不仅仅是减轻干扰,这可以提升SU的频谱效率。
2 干扰分析和频率动态分配
2.1 同频波束间距离分析
在认知卫星网络中,两个卫星系统之间实时共享卫星星历和频率配置方案等信息。由卫星星历可计算卫星在ECEF坐标系中的坐标,进一步可根据波束指向获得波束中心点的坐标,从而可得到两个系统同频波束之间的距离。
2.1.1 卫星的ECEF位置矢量
卫星的平均角速度为
式中:a为半长轴;μ=398 600.5×109m3/s2。轨道的历元时刻与起始历元时刻间隔为
tk=t-tp
式中:tp为过近地点时刻。卫星平近点角为Mk=M0+n0tk
式中:M0为平近点角。由卫星平近点角计算偏近点角的公式为
Ek=Mk+esinEk
式中:e为偏心率,该计算过程需要用到迭代法。由偏近点角计算真近点角的公式为
由真近点角计算升交距角的公式为
uk=fk+ω
式中:ω为近地点幅角。由偏近点角可得出卫星的矢径为
rk=a(1-ecosEk)
由此可得出卫星在轨道平面中的坐标为xk=rkcosuk和yk=rksinuk;则卫星在ECEF坐标系下的位置矢量为
式中:i0为卫星轨道倾角;Ωk为修正的升交点赤经,Ωk=Ω0-Ωe(tk-tp);Ω0为升交点赤经。
2.1.2 卫星的ECEF速度矢量
由以上卫星位置矢量的表达式可对卫星的速度矢量进行推导,对偏近点角求导为
(1)
对升交距角求导为

(2)
对卫星矢径求导为
(3)
由此可得卫星在轨道平面中的速度矢量的坐标为
(4)
则卫星在ECEF坐标系下的速度矢量为
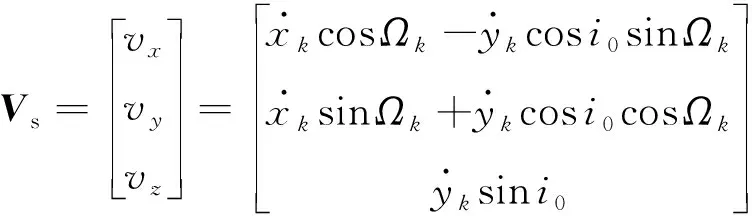
(5)
式中:在变量符号上加点表示求导。
2.1.3 波束的指向矢量
假设波束的指向矢量为
(6)
定义波束的俯仰角ψe为波束指向与卫星和地心连线的夹角(0≤ψe≤90°),方位角ψa为波束指向在过卫星点的切平面上的投影与卫星速度矢量的夹角(-180°≤ψa≤180°)。根据空间向量关系可以得到式(7),对其进行求解可获得波束的指向矢量。
(7)
2.1.4 波束中心点的位置坐标
波束照射在地表上,假设其中心点的位置坐标为
(8)
根据卫星空间向量关系可以得到式(9),对其进行求解可获得波束中心点的位置坐标为
(9)
2.1.5 不同波束中心点之间的曲面距离
根据几何关系,可以得到GEO卫星和LEO卫星同频波束的中心点间的地表距离为
(10)
式中:Ri,L和Ri,G分别为LEO和GEO卫星的波束中心点的位置坐标。
2.2 干扰分析模型
本文以用户接收到的信号功率与干扰加噪声功率之比(Signal to Interference plus Noise Ratio, SINR)作为信号质量的指标,其计算公式为
(11)
式中:P为发射功率;GT为发射天线的增益;GR为接收天线的增益;L为自由空间传播损耗;Tn为接收机的等效噪声温度;B为转发器带宽;k为波尔兹曼常数。下标中的D表示信号链路,I表示干扰链路。
自由空间传播损耗的计算公式为
(12)
式中:f为频率;d为收发双端之间的距离;c为光速。
天线增益的计算公式为[33]
(13)

(14)
式中:D为天线口径;η为天线效率。
通过分析可以得知SINR的值主要取决于信号链路和干扰链路中多个收发端之间的距离d和夹角θ,由于LEO卫星的运动特性,因而d和θ会随着相对位置的变化而变化。此外,由于GEO和LEO用户的天线设定为一直指向各自的卫星,因而其信号链路中接收端的θ恒为零。
2.3 用户最差信号质量的场景分析
在LEO卫星运行过程中,当LEO波束接近GEO同频波束时,干扰会逐渐变强,用户接收信号的质量也会相应下降。在LEO卫星运行的每一时刻,对于GEO和LEO用户都会分别存在一个位置使得位于该点的用户信号质量最差。提出用户最差场景的意义在于,只要位于最差位置的用户的信号质量高于门限,则卫星波束内服务的其他用户一定会高于门限,这样同频干扰造成的影响就满足要求。
如图2(a)中左侧的LEO卫星和GEO用户所示,当LEO卫星离GEO卫星较远时,如果GEO用户位于GEO波束的边缘,根据卫星和用户的相对位置关系,对于干扰链路,此时发射天线的夹角θT,I最小,距离dI最小,接收端的夹角θR,I最小,发射端天线增益GT,I最大,自由空间传播损耗LI最小,接收端天线增益GR,I最大,因而干扰链路的接收功率最强;对于信号链路,此时发射天线的夹角θT,D最大,距离dD最大,而接收端的夹角θR,D恒为零,此时发射端天线增益GT,D最小,自由空间传播损耗LD最大,接收端天线增益GR,D保持不变,因而信号链路的接收功率最弱。综合来看,SINR的值由信号链路的接收功率和干扰链路的接收功率决定,而信号链路的接收功率最小,干扰链路的接收功率最大,因而此位置的GEO用户的信号质量最差。
如图2(a)中右侧的LEO卫星和GEO用户所示,当LEO卫星进入GEO波束后,如果GEO用户位于GEO和LEO卫星连线的延长线上,根据卫星和用户的相对位置关系,对于干扰链路,此时接收端的θR,I为0°,发射端增益最大。根据几何关系可以看出,发射端的夹角θT,I较大,而接收端的夹角θR,I较小,θT,I的变化带来的天线增益变化较小,因而这里考虑的最差场景是θR,I为0°,此时发射端增益GT,I最大,自由空间传播损耗LI的变化范围只有数个dB,因而近似认为干扰链路的接收功率最强。类似的,对于信号链路,考虑到GEO波束张角即为GEO卫星天线的3 dB波束张角θG,3 dB,此时发射天线的夹角θT,D小于θG,3 dB,接收端的夹角θR,D恒为0°,发射端天线增益GT,D变化范围在3 dB以内,接收端天线增益保持不变,而自由空间传播损耗LD的变化范围只有数个dB。综合来看,GEO用户位于此位置时,信号链路的接收功率强度几乎不变,干扰链路的接收功率最大,因而此位置的GEO用户的信号质量最差。
通过对卫星和用户位置关系的几何分析,得到GEO用户信号质量最差情况下的夹角和距离如下:

图2 信号质量最差情况下的几何关系Fig.2 Geometric relations in poorest signal quality
1)当LEO卫星在GEO波束外面时
θT,D=0.5θG,3 dB
(15)
(16)
(17)
(18)
θR,I=l/r+θT,I+θT,D
(19)
θR,D=0°
(20)
2)当LEO卫星在GEO波束内时
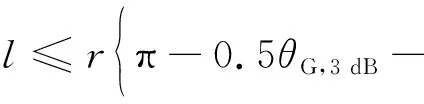
(21)
θT,I=arcsin[(r+hG)sinθT,D/(r+hL)]
(22)
(24)
θR,D=θR,I=0
(25)
式中: 下标中的T和R分别表示与发射端和接收端;D和I分别表示信号链路和干扰链路;hG和hL分别为GEO和LEO卫星的轨道高度;r为地球半径;θG,3 dB为GEO卫星的3 dB波束宽度;l为GEO和LEO的波束中心点之间的距离。
与GEO用户类似,LEO用户信号质量最差的场景如图2(b)所示。同样LEO用户信号质量最差情况下的夹角和距离也可经过几何分析得到
1) 当LEO卫星在GEO波束外面时
θT,D=0.5θL,3 dB
(26)
(27)
(28)
(29)
θR,I=l/r+θT,I-θT,D
(30)
θR,D=0°
(31)
2) 当LEO卫星在GEO波束内时

(32)
θT,D=arcsin[(r+hG)sinθT,I/(r+hL)]
(33)
(34)
(35)
θR,D=θR,I=0°
(36)
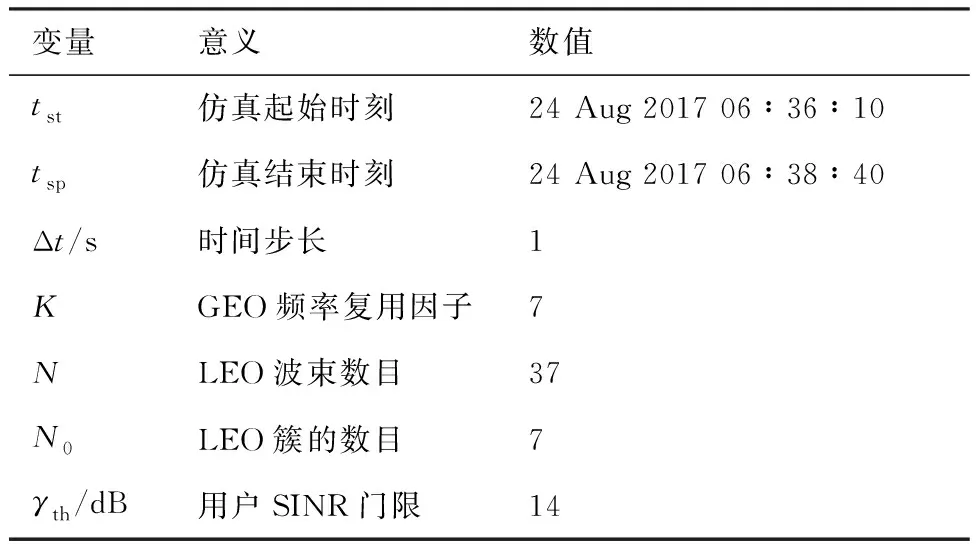
GEO和LEO卫星系统参数和轨道参数分别如表1和表2所示,经过计算得到GEO和LEO收发端的一系列夹角和距离,再分别代入式(15)、式(13)和式(14),最后代入式(12)。经过计算仿真,得到GEO和LEO用户的SINR与GEO和LEO波束距离之间的关系如图3所示。
仿真结果表明,当GEO和LEO波束间距离小于400 km时,此时LEO波束与GEO波束发生重叠,同频干扰非常严重,两个系统的用户都无法正常工作。随着距离的增加,SINR会迅速增加直至饱和。可以知道,当来自不同卫星的同频波束足够远时,干扰几乎可以完全避免,因为即使在信号质量最差的场景下SINR仍然很高。因此,本文提出波束“隔离区域”的理念,将可实现双系统共存的最小波束间距离定义为隔离距离,如图4所示。在LEO卫星的运行过程中,只要波束没有进入同频GEO波束的隔离区域内,即可实现两个系统间的频谱共享。

表1 GEO和LEO卫星系统参数Table 1 Parameters of GEO and LEO satellite systems
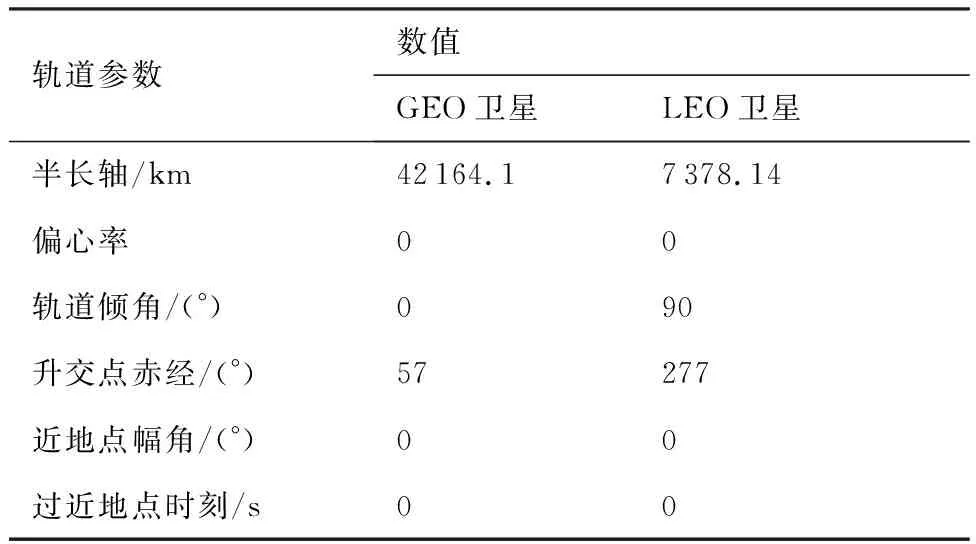
表2 GEO和LEO卫星的轨道参数Table 2 Parameters of GEO and LEO satellite orbits
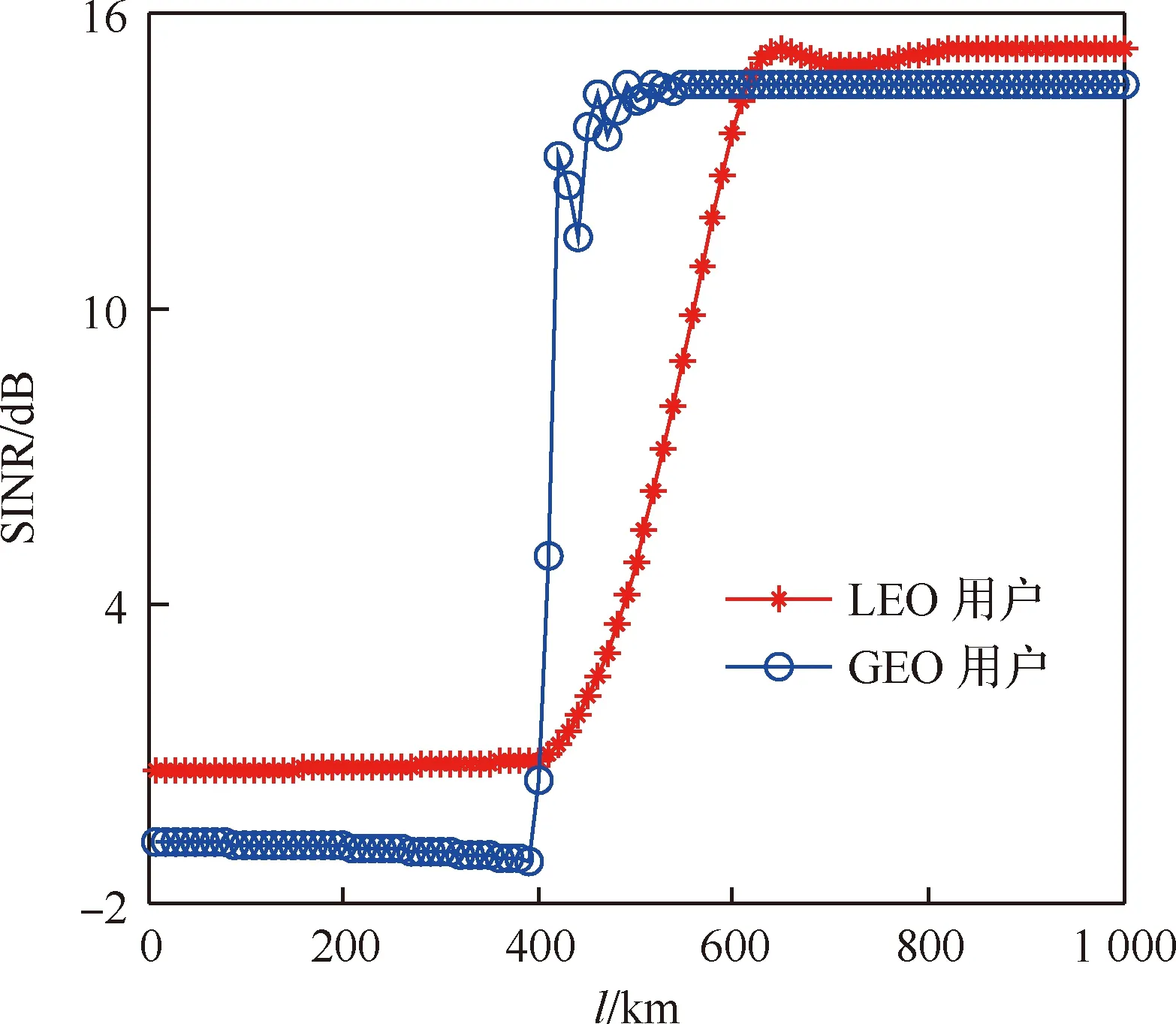
图3 SINR随l变化情况Fig.3 Variation of SINR with l

图4 隔离区域示意图Fig.4 Illustration for isolated area
2.4 频率动态分配算法
考虑到LEO卫星的运动特性,在隔离区域的基础上,论文提出一种频率动态分配算法来实现两个系统的频谱共享。双卫星系统基于数据库的方式实现认知,即系统之间通过信关站互联来共享卫星星历、频率配置方案、天线方向图等数据[29]。在前文中已经分析过,由卫星星历可计算卫星在ECEF坐标系中的坐标,进一步可根据波束指向获得波束中心点的坐标,两个波束之间的距离也可得到。在LEO卫星运行过程中,当LEO卫星的任一波束即将进入同频GEO波束的隔离区域时,必须改变该LEO波束的频率。此外,由于LEO卫星自身的波束之间也进行频率复用,单个波束的频率改变必然会对相邻波束造成影响,最终引起一连串波束频率的变化,导致所有LEO波束的频率都需要重新考虑。
令xij∈{0,1}表示波束i的频率是否为j,dij表示波束i与最近的频率为j的GEO波束中心点之间的距离。为了最小化干扰,本文以所有LEO波束与同频GEO波束之间的总距离最大化为优化目标,则频率分配方案可建模为以下优化问题,即
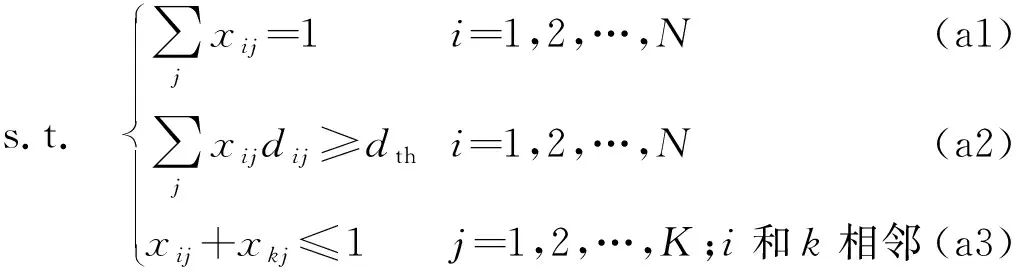
(37)
式中:N为LEO波束的数目;K为GEO卫星的频率复用因子;dth为隔离距离。通过约束条件(a1)来保证每个LEO波束都被分配了频率,且只分配了一个频率,约束条件(a2)用来保证每个LEO波束与同频GEO波束之间的距离都不小于隔离距离,约束条件(a3)确保了相邻的LEO波束之间没有分配相同的频率,其中LEO波束都是固定点波束,波束之间的相对位置保持固定,相邻的波束信息是已知的。
对于式(37)的0-1整数线性规划问题,隐式枚举法是常用的解决方法[34]。然而其计算量随N呈指数增加。此外,由于LEO卫星是动态的,波束中心点的位置也一直在变化,如果式(37)每时刻都进行一次优化,其运算量是极其庞大的,并且波束频率的切换会非常频繁。对此,本文基于波束分簇的思想提出如表3所示的算法来实现频率动态分配。
表3所示算法中,以隔离距离dth、系统的运行时间T0为输入,每个波束的频率分配信息xij为输出。首先,依照步骤4,将所有LEO波束按照七色复用的图案划分为多个簇,如图5所示。在初始化阶段对LEO波束的频率进行预分配,依照步骤5~步骤7,采用隐式枚举法对每个簇的波束进行频率分配,获得LEO所有波束初始时的频率分配信息。在LEO卫星运行过程中,再根据LEO卫星的运动轨迹,在每个时刻都进行预测分析,如步骤8~步骤12,当某一LEO波束即将进入同频GEO波束的隔离区域时,即满足步骤9所示的条件,应当判断该波束属于哪个簇,并针对该簇进行频率的重新分配。如果在下一个时刻没有出现LEO波束即将进入同频GEO波束的隔离区域的情况,即没有满足步骤9所示的条件,则继续维持该频率方案。以此往复,在LEO卫星的运动过程中根据星历和频率信息进行预测,适时地重新分配LEO波束的频率。需要指出的是,算法中输入的时间参数T0,是为了方便表示取的某一段时间,在实际中对应着系统一直运行的时间,即在系统运行的每个时刻都进行判断,如果LEO和GEO同频波束没有出现冲突,则维持该频率方案,如果出现冲突,则重新分配频率,即频率分配调整的间隔周期是根据实际情况不断变化的。
表3 基于波束分簇的频率动态分配算法
Table 3 Frequency dynamic allocation algorithm based on beam clustering

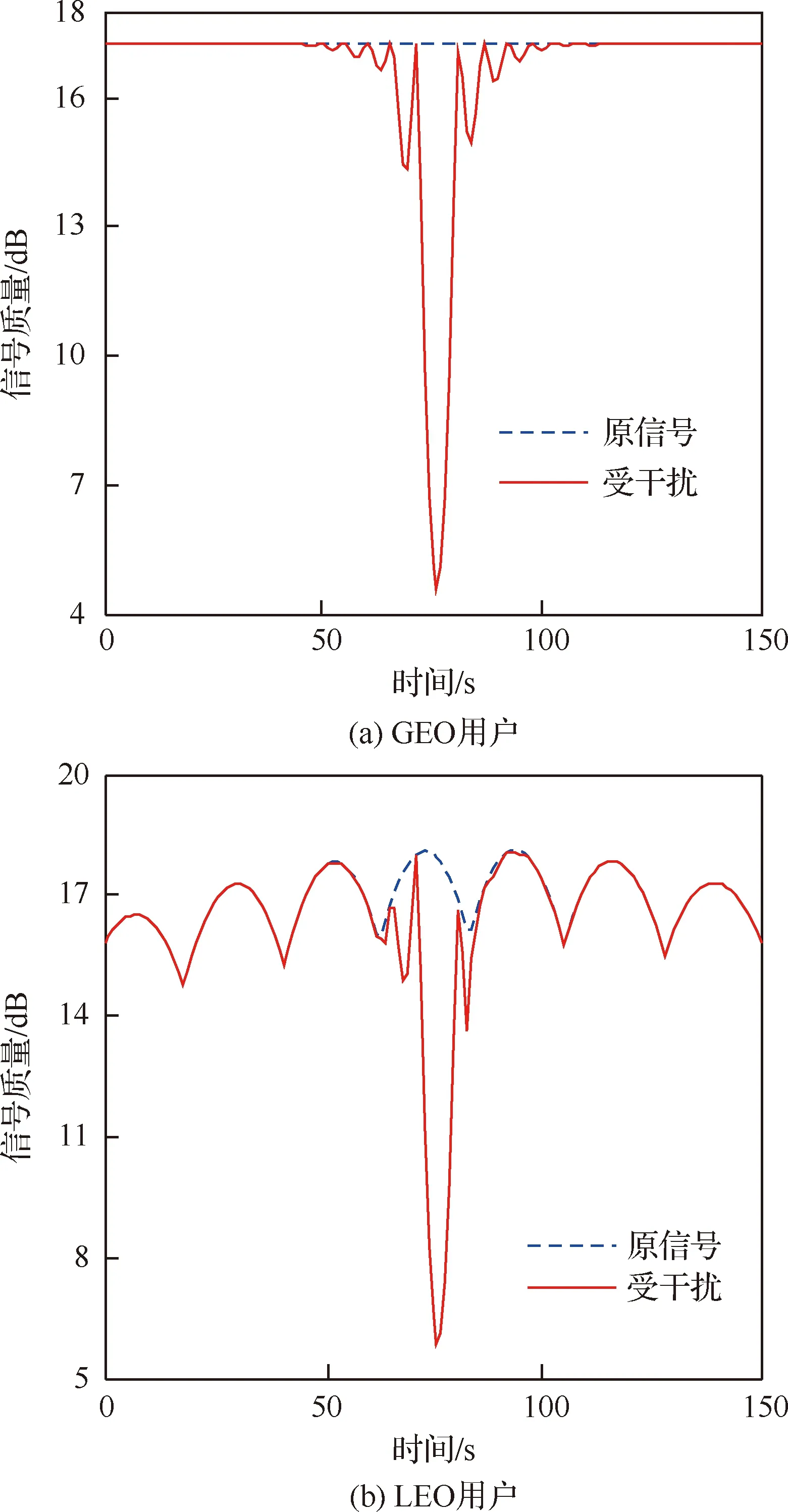
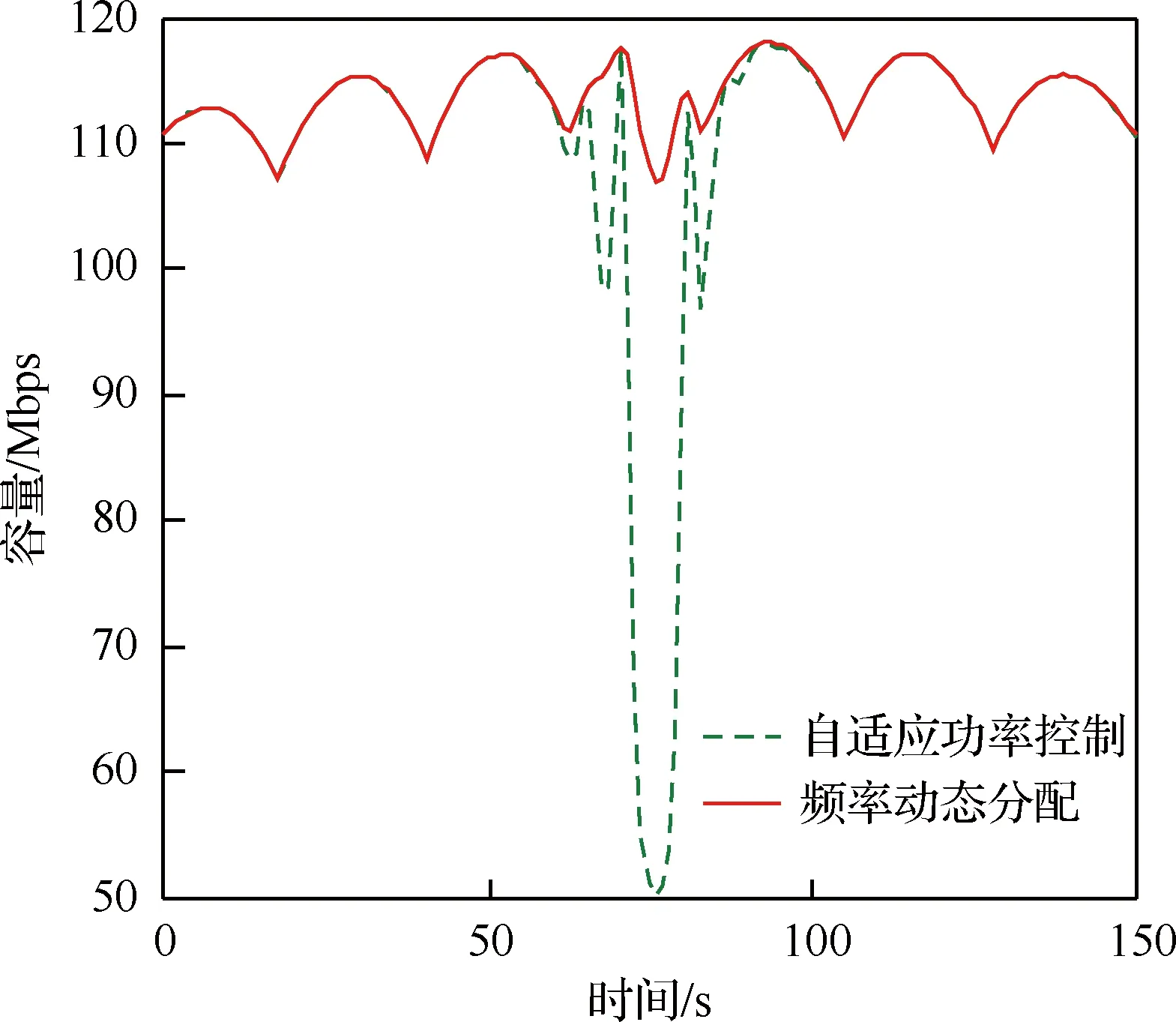
步骤内容1输入:dth, T02输出:xij3开始4将LEO波束按照七色复用的图案分为N0个簇5循环 a=1,2,…,N06根据式(37)采用对每个簇的波束进行频率分配7结束循环8循环 t=1,2,…,T09如果 ∃i0∈i,s.t.∑jxijdij 图5 按照七色复用划分簇Fig.5 Cluster of seven color multiplexing 如果在LEO卫星运行过程中每个时刻都进行一次频率分配,则每个时刻都需要对式(37)进行求解,并根据其最优解对所有波束的频率进行分配,因此会存在大量波束的频率时刻改变的情况,从而造成波束频率的频繁切换。如果采用算法1的思想,只需要在LEO和GEO同频波束出现冲突时依据式(37)进行频率重新分配,在没有冲突的时刻依然维持上一时刻的频率方案,因而在大多数时刻并不需要进行频率重新分配。在此基础上,进一步引入波束分簇的思想,那么每次LEO和GEO同频波束出现冲突时,只需要对引起该冲突的波束所在簇进行频率重新分配,其余波束仍保持不变,这样调整频率的波束只占到原本所有波束的几分之一,从而可以进一步减少波束频率的切换次数。 如果直接采用枚举法解算问题式(37),其时间复杂度为:o(2NK)。若引入隐式枚举法的思想,剪掉搜寻最优解过程中的多余分支,则可以压缩计算量。具体而言,针对约束条件(a1),可以知道知道当i固定时,对于多个xij只有其中一个取值为1,其余为0,在此基础上对枚举法进行优化,得到的复杂度为:o(KN)。需要注意的是,这只是单次波束分配的复杂度,随着卫星的运动,如果每过一个时刻都进行一次频率分配,则总复杂度为o(T0KN)。在引入波束分簇思想后,单次波束分配的复杂度为o(K7N/7),卫星运行一段时间的总复杂度为o(K7N/7+T0K7ε),其中o(K7N/7)为频率分配初始化的复杂度,o(K7ε)为每个时刻需要重新频率分配的复杂度,ε为需要重新分配的簇数目,取值范围为0~N/7,且在大多数时刻为0。 为便于仿真,仿真时间设定为LEO卫星的一次过顶时间,GEO和LEO用户都位于GEO中间波束的中心点,具体参数如表4所示。 首先,针对GEO和LEO系统之间进行频谱共享的同频干扰情况进行分析。图6为仿真期间GEO和LEO用户的信号质量变化情况,其中虚线表示频谱只分配给该系统时用户的信号质量,实线表示在不采取保护措施条件下两个系统共用频谱时用户的信号质量。由于GEO卫星的相对地面保持静止,GEO用户的原信号质量几乎没有变化,而LEO用户的原信号质量随着多个波束依次过境呈现周期性。当LEO和GEO系统共用频率时,由于相互之间的同频干扰,信号质量会下降,并且随着LEO卫星的运动而变化。当两个系统的卫星和用户共线时,同频干扰最为严重,信号质量严重恶化,此时可能会导致系统瘫痪。 表4 仿真参数Table 4 Simulation parameters 图6 受同频干扰的用户信号质量Fig.6 Signal quality affected by co-channel interference 其次,对基于波束分簇的频率动态分配算法进行了仿真。根据图3中SINR与距离的关系,结合用户所需的SINR门限,这里选择600 km作为dth。在仿真周期中,簇层次的频率分配有9次,波束层次的频率分配有50次,远小于每秒钟都进行分配的频次。此外,在双卫星频谱共享中常用的方法包括自适应功率控制方法,该方法在两个卫星系统引发冲突时,通过自适应减小次级用户的发射功率,使得主用户的SINR不低于门限,即牺牲次级用户的性能来保证主用户的正常工作,从而实现双卫星之间的频谱共享[27]。将本方法与自适应功率控制方法进行对比,如图7所示。其中,虚线表示采用自适应功率控制时用户的信号质量,实线表示采用频率动态分配时用户的信号质量。当两个系统共享频谱时,会发生同频干扰,如果采用自适应功率控制方法,由于对GEO用户的保护机制,LEO用户的SINR会下降很多,如图7(b)虚线所示。实线中GEO用户的信号质量几乎完全与原信号一样,而LEO用户的SINR也一直高于门限,表明本文提出的基于频率动态分配的频谱共享方法性能优越。 进一步对用户在理想条件下的信道容量进行分析,计算公式为式(38)。通过仿真,得到GEO和LEO用户在理想条件下总的信道容量如图8所示。相较于自适应功率控制方法,由于避免了共视干扰,网络的信道容量得到了有效提升,最大时可提升一倍以上。 (38) 图7 不同方法用户信号质量随时间变化Fig.7 Variation of signal quality with time for different methods 图8 不同方法用户信道容量随时间变化Fig.8 Variation of capacity with time for different methods 本文对空间信息网络中的频谱共享进行了研究。针对GEO和LEO双卫星系统共存的场景提出了一种新型动态频谱共享方法,得到以下结论: 1) 相较于实时的频率动态分配算法,能够在提高网络容量的同时,降低波束频率的切换频次。 2) 相较于常用的自适应功率控制方法,次级用户的信号质量得到有效提升。 3) 相较于自适应功率控制方法,整个网络的信道容量得到了有效提升,最大时可提升一倍以上。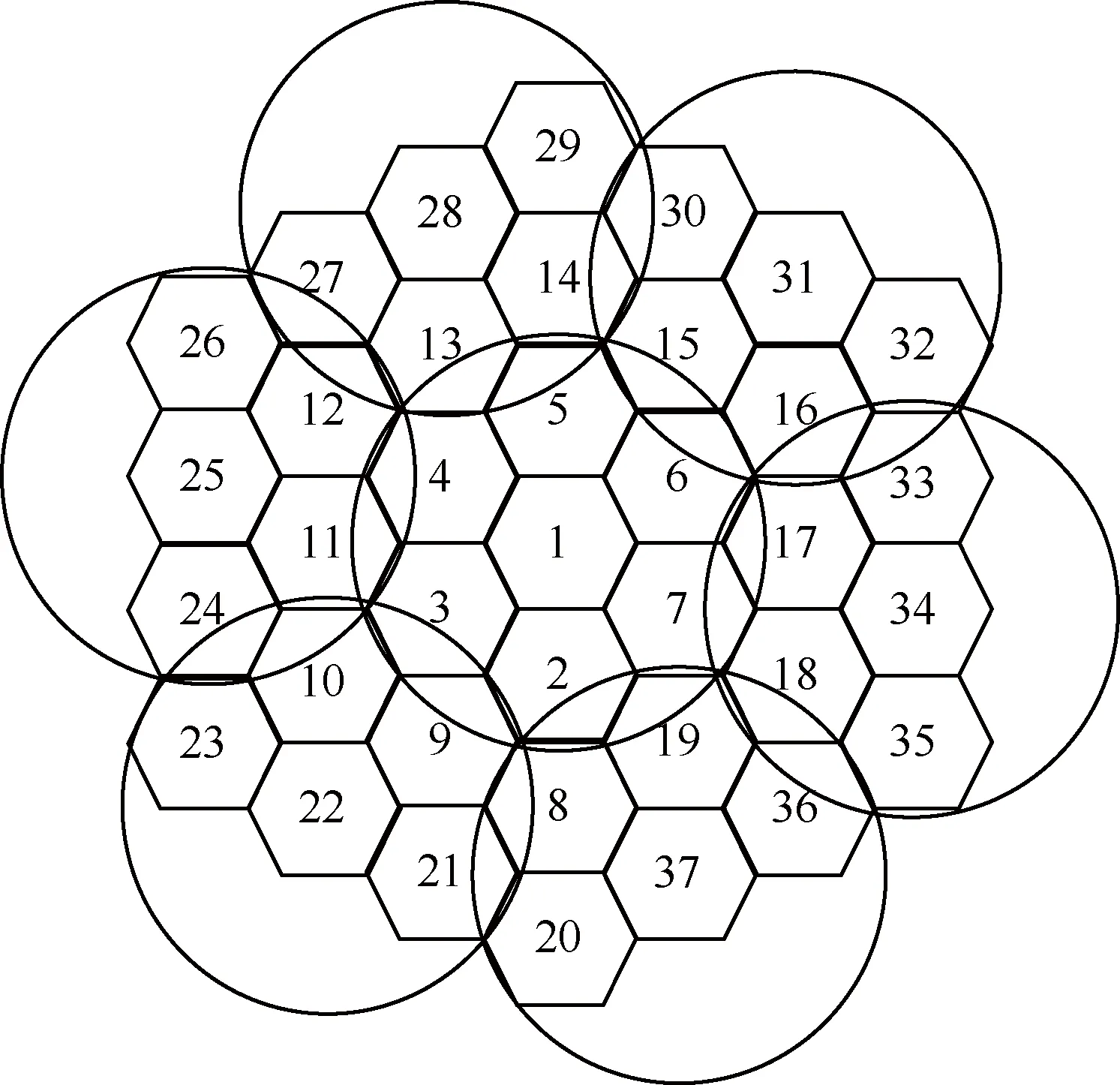
3 频谱共享仿真分析


4 结 论

