基于深度学习的地空导弹发射区拟合算法

高晓光，李新宇，岳勐琪，张金辉，赵利强，吴高峰，李飞

1. 西北工业大学 电子信息学院，西安 710072 2. 航空工业洛阳电光设备研究所，洛阳 471000 3. 中国空空导弹研究院，洛阳 471009

地空导弹是从地面(地上、地下、车上等)发射、攻击空中和太空目标的导弹，当前主要用来防御航空兵器[1]。地空导弹的发射区是一项提供给指挥员进行导弹发射时机判断的重要参数，发射区的解算精度直接影响到导弹的攻击效果。

早期为了获取地空导弹发射区的工作式，多采用多项式拟合的方法。从文献[2]中可以看出，多项式拟合需要从大量训练数据中分析各输入参数与发射区的关系。由于地空导弹发射区的输入参数较多，且部分输入参数与发射区的关系并不直观，因此很难通过直接观察得到一个合适的工作式，且拟合精度较低。针对以上问题，有学者另辟蹊径，选用神经网络对发射区进行拟合[3]。神经网络可以通过隐层来提取输入参数的特征，表征输入与输出之间的关系，不需要构造具体的工作式，从而有效地避免了工作式选取过程的巨大工作量，文献[4-8]也均指出神经网络能够用于解决该类非结构性问题。但神经网络是一种浅层网络，在面对大量且关系复杂的数据时，其提取数据特征的能力有限，拟合效果存在瓶颈，当隐层节点数达到一定程度后，拟合精度很难得到提升。当隐层节点数过多时，网络训练时间将大大增加，还可能出现过拟合问题[9]。同时，神经网络的训练需要大量的标签数据，这极大地增大了实际应用的人工成本。

传统方法在对导弹发射区拟合时存在不足：

1) 多项式拟合算法无法应对多维输入。多项式拟合算法需要人工设计工作式，即人工设计输入数据与输出数据之间的依赖关系。当输入数据维度较低时，这种方法通常是可行的，并且可以保证一定精度；而当输入数据维度增加时，输入与输出之间的依赖关系式很难通过直观的方式进行设计，这很大程度上限制了多项式拟合算法的应用场景和拟合精度。

2) BP (Back Propagation)神经网络存在拟合精度限制。传统BP神经网络为三层神经网络，虽然在理论上，当隐层节点数目无限增多时，可以以任意精度逼近任意非线性函数，但在实际应用中，这种条件是无法实现的。因此，当BP神经网络的拟合精度达到一定程度时，再想进一步提高，需要付出大量的模型结构代价和计算代价，尤其是增加网络深度时容易出现梯度弥散现象，反而使训练效果变差，这极大地限制了BP神经网络在高精度需求下的应用。

3) 深度BP神经网络等监督学习算法需要大量的标签数据。由于BP神经网络属于监督模型，所需的大量训练数据必须具有标签。在实际军事应用中，有时很难采集到大量标签数据，若使用深层BP神经网络进行训练，则必须对无标签数据进行人工标注，此时的人力成本过大，如针对地空导弹发射区问题，数据的标签往往通过实弹打靶、专家经验等方式获得，在一些情况下很难完成，进一步加大了获取深度BP神经网络训练数据的难度。

针对以上描述的问题，本文设计了一种基于堆栈稀疏自编码器 (Stacked Sparse Auto Encoder, SSAE) 的深度拟合网络 (Deep Fitting Network, DFN)，简称SSAE-DFN，并将其应用于地空导弹发射区的拟合问题中。SSAE是一种深层神经网络模型，结构上由多个AE (Auto Encoder) 模型堆叠而成，并加入稀疏性限制，具有无监督学习的特性[10]。Hintong和Salakhutdinov[10]表明了两点关键信息：① 多隐层的人工神经网络具有优异的特征学习能力，学习得到的特征对数据有更本质的描述；② 可通过“逐层初始化”(Layer Wise Pre-training)来解决深度神经网络训练困难的问题。在表达相同的非线性函数时，深层网络比浅层网络所需的节点数更少。本文所设计的深度拟合模型相对于传统算法具有以下优势：

1) 可以有效应对多维输入。深度拟合网络的工作机制是通过对数据的学习来自动建立输入与输出之间的依赖关系，所以理论上可以应对任意维的输入，从而克服了多项式方法的不足。

2) 提高拟合精度。多层深度拟合网络具有更强的表达能力，可以拟合更加复杂的非线性函数。通过多隐层提取更准确的数据特征来最终提高拟合精度。从而突破了传统BP神经网络的拟合精度限制。

3) 减少对标签数据的依赖。针对地空导弹发射区问题，本文提出的深度拟合网络首先通过无监督学习的方式进行预训练，即使用大量无标签的预训练数据，将模型训练到一个较好的状态；之后，在监督学习的方式下对网络进行微调，此过程只需要少量的标签数据即可完成对发射区的拟合。相较于BP神经网络，本文提出的深度拟合网络大大减少对标签数据的依赖，节约了人力、缩短了实验流程，更避免了不必要的资源浪费。

1 问题描述

地空导弹发射区是一片空域范围，目标在发射区内部时，由地面发射的地空导弹将与目标在杀伤区相遇[11]。根据地空导弹发射区获取途径的不同，可以分为理论发射区和实际发射区。理论发射区通过导弹研发方根据导弹的各项性能参数进行计算获得，而实际发射区则是根据理论发射区数据，通过一定的解算方法得到。地空导弹实际发射区的解算精度表现为其与理论发射区的契合度，两者越接近说明解算精度越高。本文后续部分中所提及的地空导弹发射区，除特殊说明外，均指地空导弹实际发射区。

对地空导弹发射区的拟合，实际上是寻求一个最优的函数形式来有效地表达各项输入参数值与发射区数值之间的关系。假设空中目标A高度为H，速度为V，则其与地空导弹的位置关系在水平面的投影可如图1所示。其中，TD为目标航向在水平面投影，地空导弹位置为O，安装轴线方向为Ox。导弹离轴角是导弹发射方向与目标方向的夹角，如图中θ所示，导弹发射离轴角有限，最大离轴角记为θmax，于是可以根据TD的不同和导弹发射距离的限制，可以获得KLMN组成的扇形区域所示的地空导弹发射区，其中地空导弹发射位置O到MN的距离r为发射区近界距离，同理R为远界距离，而从导弹发射位置O到目标航向水平投影的垂直距离即为航路捷径，如图中P所示。

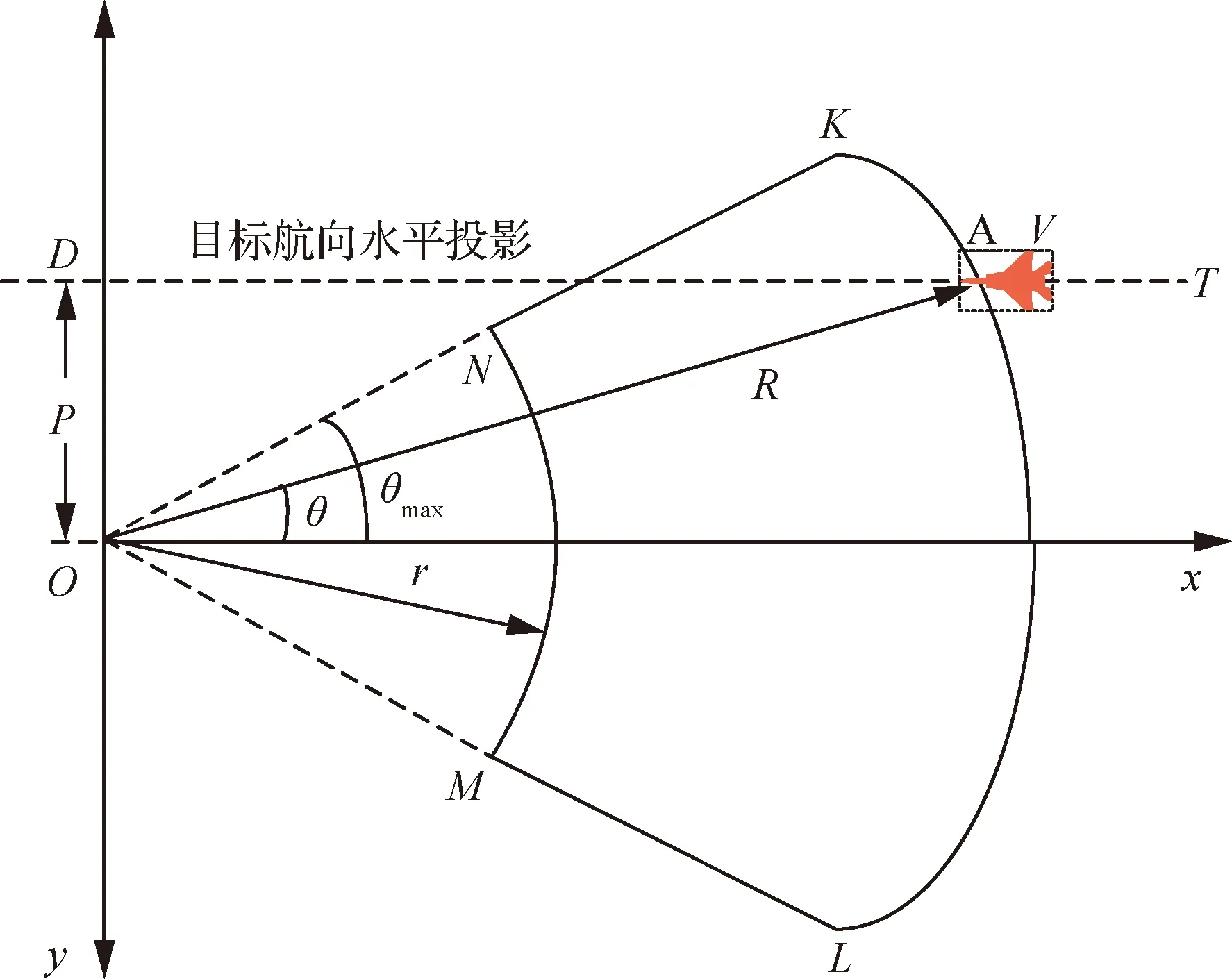
图1 地空导弹发射区水平面投影示意图Fig.1 Projection of ground-to-air missile horizontal launch zone

通过6自由度的地空导弹发射区仿真，可以得到大量理论发射区近界和远界的数据。本文选用地空导弹理论发射区远界的数据进行拟合，其数值主要与离轴角θ、目标高度H、目标速度V和航路捷径P这4个变量有关，因此地空导弹发射区远界R所需构造的工作式形式为

R=f(θ,H,V,P)

(1)

1.1 多项式拟合算法

由于多项式拟合函数可以是任意函数形式的组合，因此多项式拟合算法最大的困难在于如何寻找到合适的工作式[12]。即便是多项式次数不高的简单线性模型，随自变量数目的增加，工作式项数也会以指数形式快速增加。

对于地空导弹发射区的拟合问题，影响地空导弹发射区远界的因素主要有4个，即离轴角θ、目标高度H、目标速度V和航路捷径P，因此自变量的个数至少为4。多项式中除了简单的线性模型变量外，还可能有其他形式的多项式项，多项式的构成将变得更加复杂，多项式的选择也将变得更加困难。

以最高项为4次项的线性模型为例，构造如下的多项式对地空导弹发射区进行拟合：

R=f(θ,H,V,P)=f1(θ,H,V,P)+

f2(θ,H,V,P)+…+f3(θ,H,V,P)

(2)

可见通过多项式对地空导弹发射区进行拟合难度很大，因此需要寻找其他的方法来对发射区进行拟合。

1.2 BP神经网络算法

由于多项式拟合存在函数形式难以确定等问题，因此考虑采用神经网络对地空导弹发射区进行拟合。BP神经网络是一种按误差反向传播算法训练的多层前馈网络，是应用最为成功的神经网络，具有良好的非线性表达能力和优异的函数逼近能力[13]。神经网络没有具体的函数表达式，因此避免了工作式寻找困难的问题。

传统神经网络的结构如图2所示，图中的神经网络包含输入层(M)、2个隐层(I和J)以及输出层(N)，X=[x1,x2,…,xm]为m个输入信号，Y=[y1,y2,…,yp]为p个输出信号，wmi为输入层到隐层I的权值、wij为隐层I到隐层J的权值、wjn为隐层J到输出层的权值。于是，神经网络的输出可以表示为

Y=hW,b(X)=h(WXT+b)

(3)

式中：W为权值矩阵；b为偏置项。

神经网络通过误差反向传播算法不断修正各层之间的权值，用输出层的误差修正与输出层相连接的权值，再计算出隐层单元的误差来修正与隐层连接的权值。通过训练比较网络的实际输出与期望输出的误差，不断调整网络权值，直到输出层的误差达到预设的精度，从而得到整个网络的权值。设计神经网络的要素包含选择合理的隐层数、每层的节点数、代价函数、以及权值计算方法。

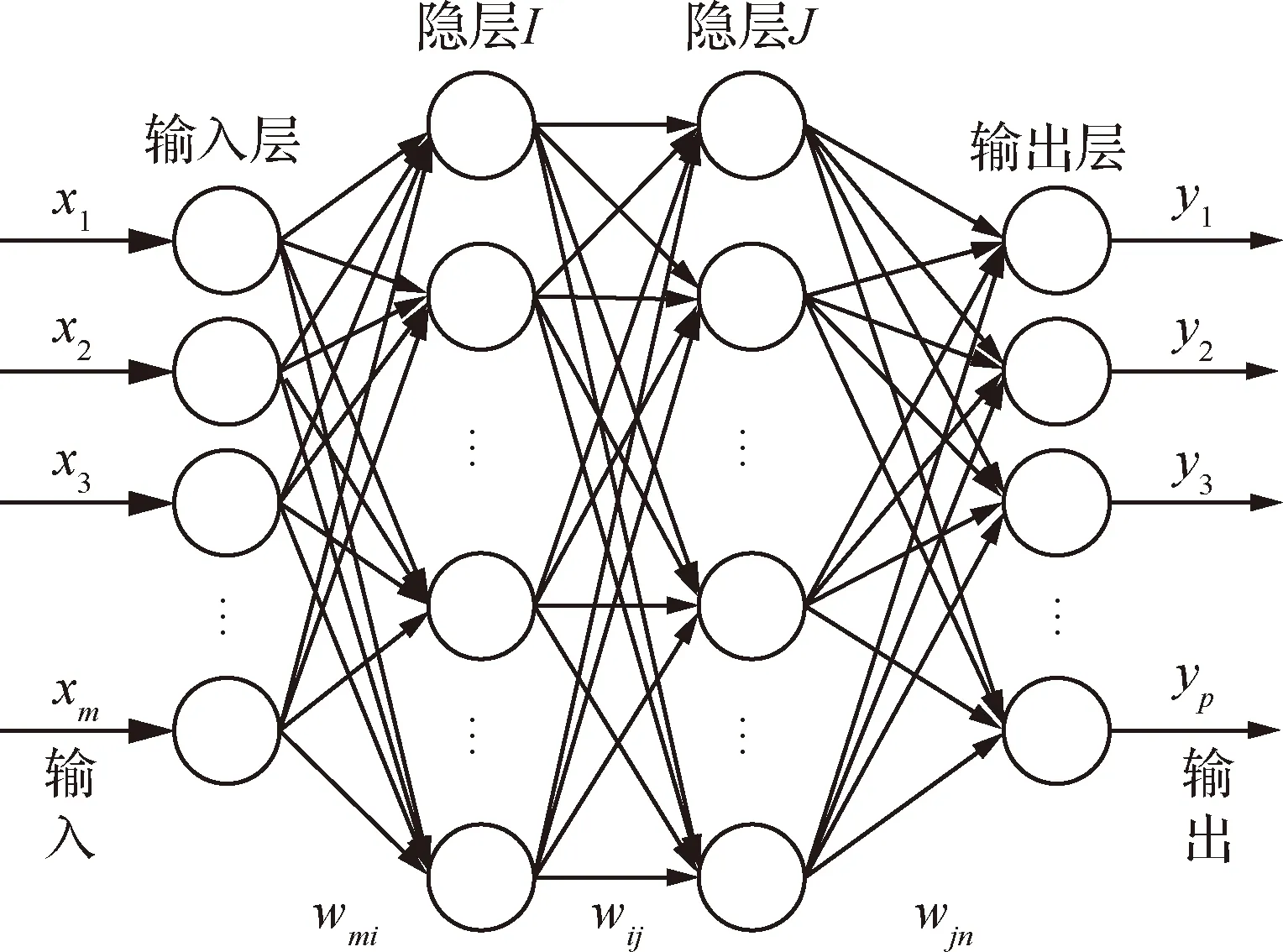
图2 传统BP神经网络结构Fig.2 Structure of traditional BP neural network

随着隐层数的增加，网络的深度也在增加，传统神经网络对于地空导弹发射区远界的拟合效果将会有一定的提升，因为深层网络相比浅层网络具备更强大的特征提取能力，但当网络深度到达一定程度后，由于BP算法本身存在梯度弥散的问题[14]，会导致训练效果较差。过多的隐层节点数也可能导致网络参数无法得到充分训练，从而使网络的拟合性能下降，因此隐层节点数并不是越多越好[15]。

正是由于BP神经网络在参数选取时存在的这些不足，本文设计了一种堆栈式稀疏自编码器网络。

2 堆栈稀疏自编码网络模型

本文设计了一种基于AE模型的SSAE深度拟合网络(SSAE-DFN)。SSAE网络由多个AE堆叠而成的，并加入了稀疏性限制对网络性能进行进一步的改善。SSAE网络具有多层非线性映射的结构，通过无监督学习方式的预训练，可以获得一定的先验知识，使网络权值处于较好的初始位置，能够较好地逼近复杂函数[16-18]。SSAE网络的基本单元是AE，下面对AE以及其相关训练算法进行介绍。

2.1 自编码器

自编码器是一种无监督学习算法模型，所使用的训练样本是无类别标签的，利用反向传播算法进行训练，用于提取训练数据的高级特征[19]，其基本结构如图3所示。

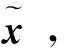
图3 自编码器的基本结构Fig.3 Basic structure of auto-encoder

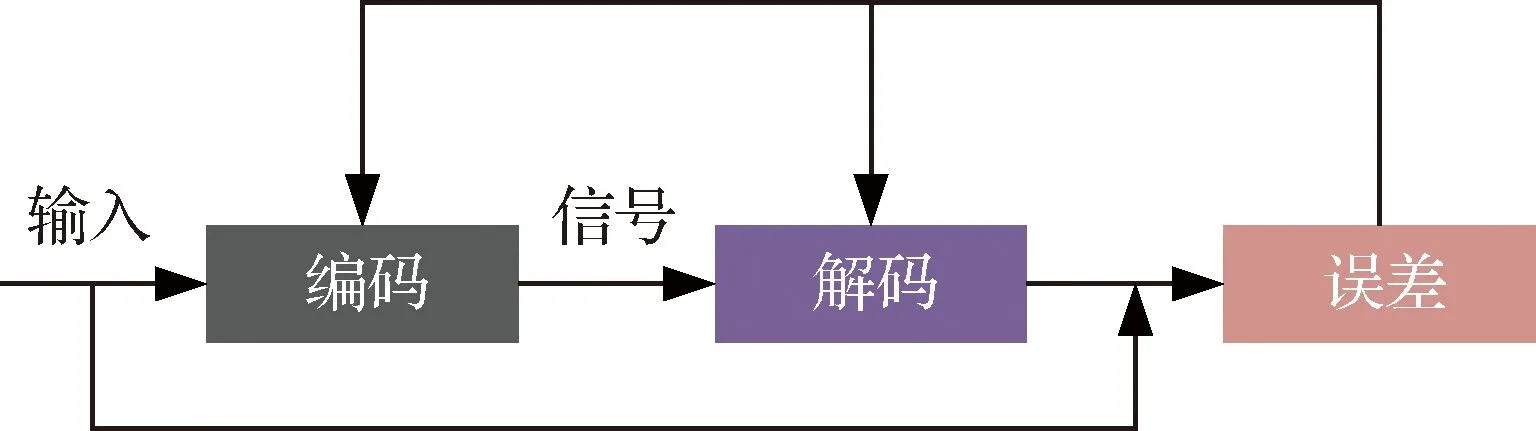
图4 自编码器网络训练的抽象表示Fig.4 Abstract representation of auto-encoder network training

自编码器的原理是将训练样本同时作为网络的输入和输出，即表征一个hW,b(x)≈x的映射关系，输入信号是原始样本的集合{x(1),x(2),…,x(n)} (x(i)∈Rm)，其中m为输入信号的维数，将这些样本从网络的输入层输入，经过非线性激励映射到隐层，这个过程被称为编码，而将隐层继续作为下一层的输入，经过非线性激励映射到输入层以重构输入数据，这个过程被称为解码，和BP神经网络的代价函数类似，由于自编码器的输入等于输出，因此其代价函数为

(4)

式中：第1项是重构误差项；第2项是正则项，用来防止过拟合；(x(k),y(k))为某一组训练样本，hW,b(x(k))为输入x(k)对应的网络输出;W为自编码器各节点之间的权重w构成的矩阵。

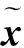
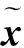
从网络整体训练的角度来看，自编码器通过训练可以改善自身的性能，学习到输入样本数据的部分特征，从而可以进一步提升深度网络的性能。在使用自编码器模型时，可以对网络加入某些特定的限制来增强网络的整体性能，Vincent等对自编码器进行了改进，提出了降噪自编码器 (De-noising Auto Encoder, DAE)，解决了在分布相差很大条件下的训练样本和测试样本训练导致的训练效果快速下降的问题[20]；而稀疏自编码器 (Sparse Auto Encoder, SAE) 是基于稀疏性思想被提出的另一个经典自编码器模型，同样得到了广泛的应用[21-22]。本文选取堆栈式稀疏自编码器对地空导弹发射区进行拟合，下面对有关SSAE的知识进行详细的介绍。

2.2 稀疏性限制

所谓稀疏性是受哺乳动物视觉系统的运作机制启发的，哺乳动物在视觉皮层中使用了稀疏性表示(Sparse Representation)，其皮层中存在的细胞感受域(Receptive Field)具有带通性(Band-pass)、方向性(Oriented)和空间局部性(Spatially Localized)，为了理解这3种性能在视觉细胞捕获到的图像中存在的内部结构之间的关系，可以通过某种编码手段来实现，利用含稀疏项的目标函数来学习训练数据的稀疏表示，可以表征以上3种 性能的相关性[23]。

假设自编码器的激励函数仍选择Sigmoid函数，神经元的输出值域为(0,1)，那么关于神经网络的稀疏性，可以在神经元的输出十分趋近于1时认为被激活，反之当神经元输出十分趋近于0时认为被抑制，从理论定义上将使神经元在大部分时间内都处于被抑制状态的限制条件被称为稀疏性限制[24]。

加入稀疏性限制，实际上是相对于多层BP神经网络在误差反向传播过程中加入了一个稀疏项，目的是为了学习到样本数据中更具一般性的特征，所谓稀疏性反映的是变量之间分布的差异，通过这些差异可以表征样本数据之间的某些相关性关系。

2.3 KL散度

KL散度(Kullback-Leibler Divergence, KLD)是信息论中的概念，在机器学习领域同样得到了广泛的应用[25]，多用于度量2个函数之间的相近程度和相似程度，在泛函分析中也经常用到[26]。

假设现在有2个关于样本集的概率分布为p和q，其中p为真实分布，而q为非真实分布，则按照真实分布p来衡量识别一个样本所需编码长度的期望(即平均编码长度H(p))为

(5)

如果使用非真实分布q来表示真实分布p的平均编码长度H(p,q)，则为

(6)

由于用q来编码的样本来自于p分布，所以期望值H(p,q)中概率是p(i),H(p,q)被称为“交叉熵”。

(7)

基于KLD理论，惩罚因子可以表示为

(8)

式中：|L2|为隐层Layer 2中神经元的数量,

(9)

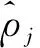
(10)

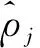
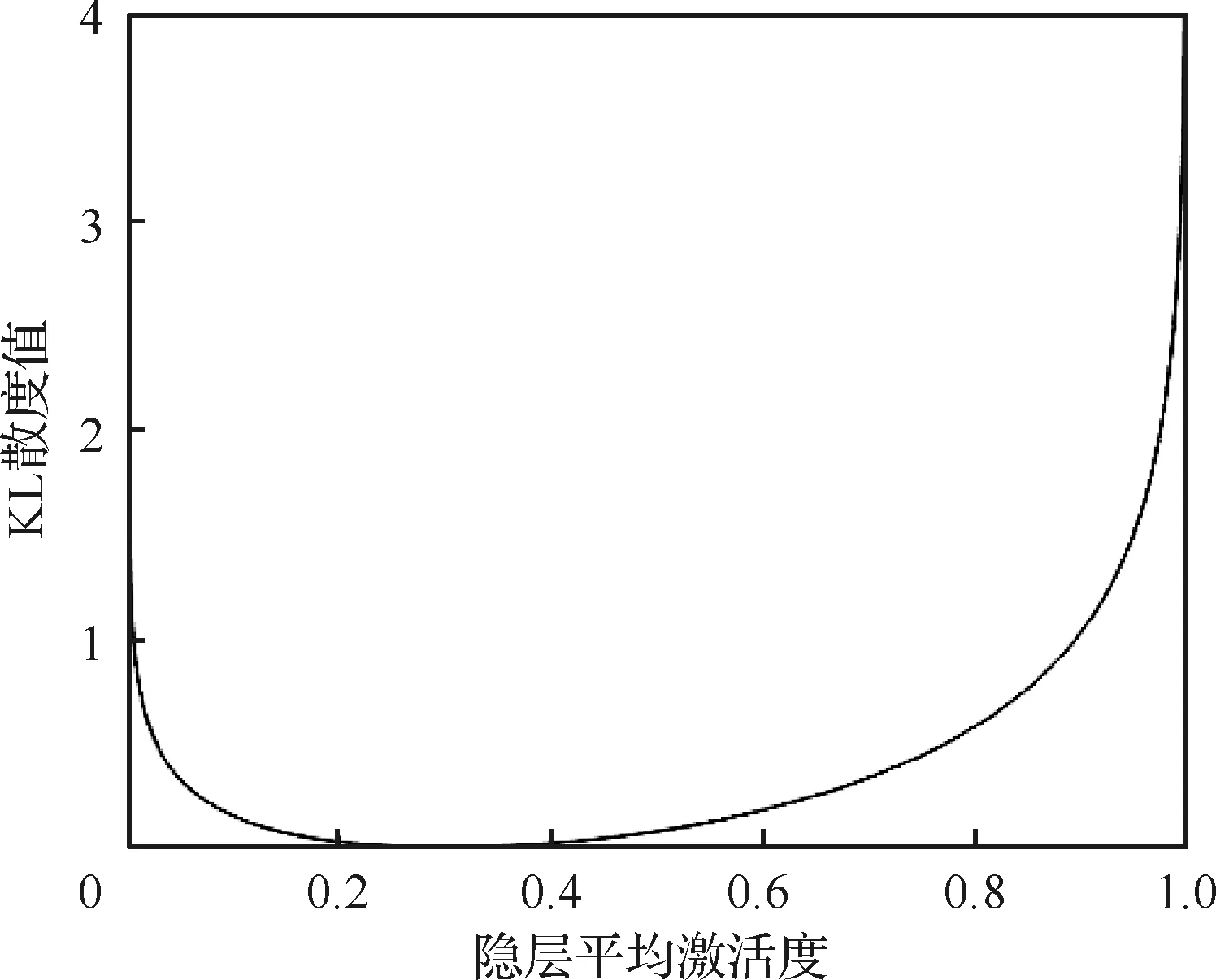
图5 KL散度值的变化趋势示意图Fig.5 Variation trend schematic diagram of KL divergence value

(11)

式中：|I|、|J|为两隐层的节点数；wj,i为神经元i和神经元j之间的连接权值。

3 训练策略

为了对比深度学习网络模型与传统神经网络对地空导弹发射区远界拟合效果的不同，选用与神经网络模型相同的训练样本，以堆栈式稀疏自编码器(SSAE)网络模型对地空导弹发射区远界进行拟合。由于堆栈式稀疏自编码器是由多个自编码器堆叠而来，故其隐层数与各隐层节点数的选取对于最终的训练结果也存在较大的影响。输入仍是由离轴角θ、目标高度H、目标速度V和航路捷径P组成的输入变量矩阵，即X=[θ,H,V,P]T，输出矩阵与输入矩阵相同，预训练过程是利用实验数据通过无监督学习对网络进行训练，使网络的权值和偏置处于一个相对较好的初值位置；当所有自编码器训练完成，得到网络的初始结构参数后，在网络顶层加入发射区远界的标签数据R对网络进行全局调优，进一步优化SSAE的网络权值和偏置，得到最终训练好的深度网络。深度网络整体的训练分为网络的预训练(Pre-training)和全局调优(Fine-tuning)两个过程，下面就深度网络模型的具体训练过程进行介绍。

3.1 确定网络结构

根据式(1)，本文使用的网络具有4个输入，1个 输出。在构建实际网络时，自编码器的隐层节点数一般比输入层节点数少。研究发现，隐层节点数多于输入层节点数时，也可以得到同样的训练效果。为了增加网络的深度，SSAE的第1层 隐层节点数选为50，这样可保证其后的隐层节点数以一定的步长逐渐减小，便于对数据进行学习。为了确定本文所使用的网络结构，本节进行了如下实验。

该实验对不同结构的网络进行精度分析，并采用平方根均方误差(RMSE)作为衡量拟合结果精度的指标。由图6可知，在训练 SSAE时，随着网络深度的增加，平方根均方误差逐渐减少，但误差下降的速率也在逐渐降低，三隐层网络到四隐层网络的误差下降速率已近似为0，故本文没有必要进行大于四隐层网络的实验。

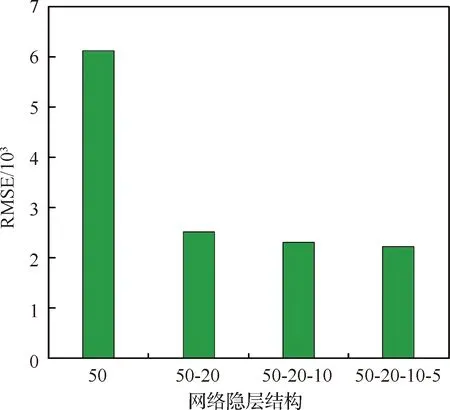
图6 不同隐层结构堆栈式稀疏自编码器平方根均方误差(RMSE)Fig.6 RMSE of stacked sparse auto-encoder with different structures of hidden layer

3.2 网络的预训练

自编码器预训练的过程是无监督的，对于地空导弹发射区样本数据来讲，仅需要利用输入变量矩阵进行训练。给定第1个自编码器的输入矩阵X(1)=[θ,H,V,P]T、隐层L(1)和输出矩阵Y(1)=X(1)=[θ,H,V,P]T，并对其进行归一化处理，并随机初始化网络参数值，对第1个自编码器进行训练，第1个自编码器的结构如图7所示。

网络的预训练实际上就是依次训练所有的AE，使网络权值处于一个相对较好的初始位置，预训练的过程是深度网络能够得到顺利训练的保证，其具体步骤为

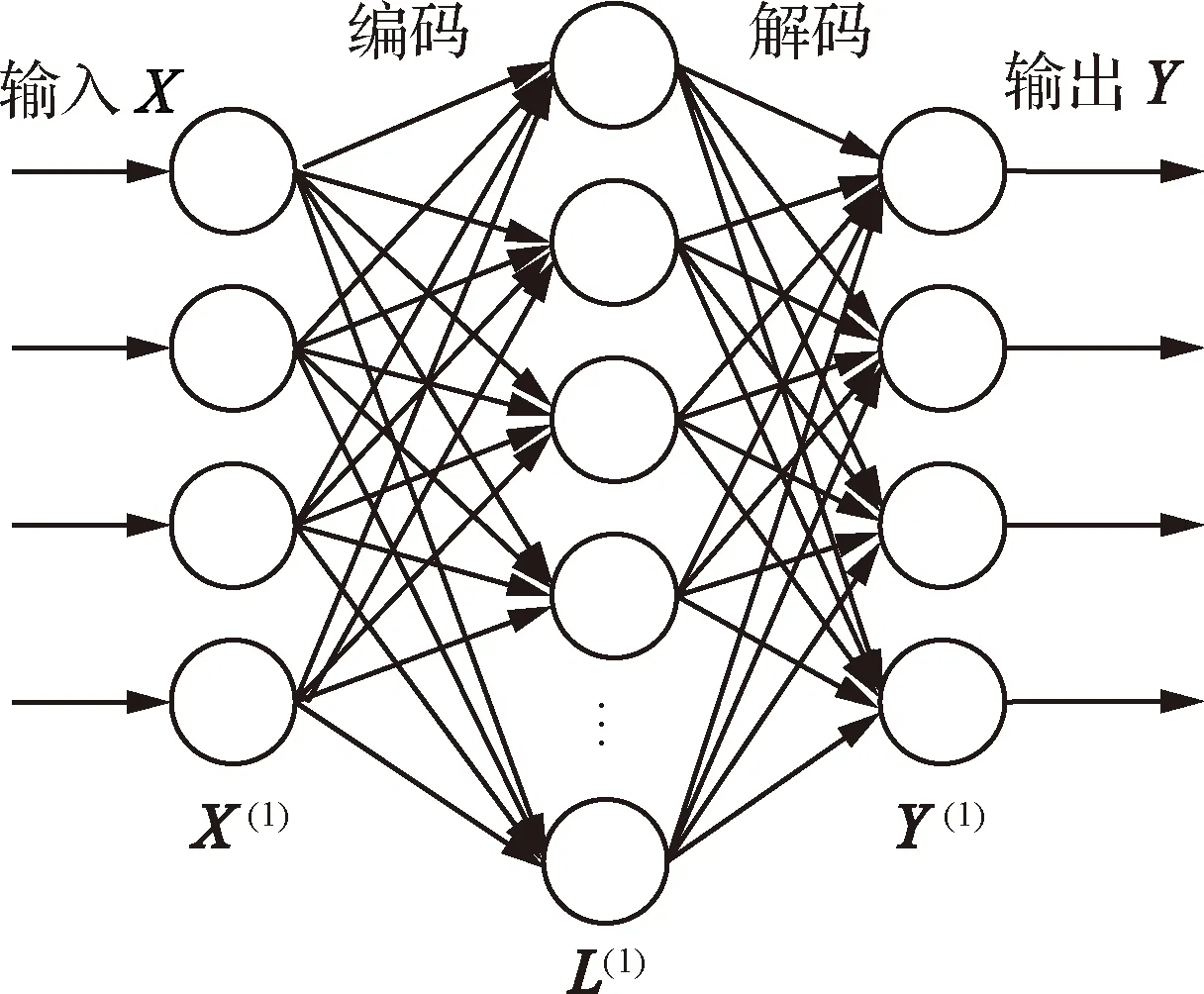
图7 深度网络第1个自编码器结构Fig.7 First auto-encoder structure of deep network

步骤1设计SSAE网络结构。为了使深度网络的拟合结果具有说服力，需要利用控制变量的思想设计一系列的深度网络结构，确定隐层数及各隐层节点数。在保证网络结构相同的前提下，对比BP算法和SSAE的拟合结果。

步骤2将地空导弹的离轴角θ、目标高度H、目标速度V和航路捷径P的数据进行归一化处理，使其数据的数值全部位于[0,1]的区间内，作为第1个AE的输入矩阵。

步骤3对第1个AE进行训练，待结果收敛后将第1个AE的隐层输出作为第2个AE的输入对第2个AE进行训练。

步骤4第2个AE训练结束后将其隐层输出作为下一个AE的输入，以此类推，直至每一个AE都训练完成。

经过以上训练后，整个深度网络可以得到一个相对较好的初始权值，接下来要对整个网络进行全局调优。

3.3 全局调优

SSAE网络经过预训练，网络权值已经位于一个较好的状态，接下来需要在顶层加入地空导弹发射区的标签数据对网络进行全局调优，需要在网络顶端加入输出层，得到了如图8所示的网络结构。

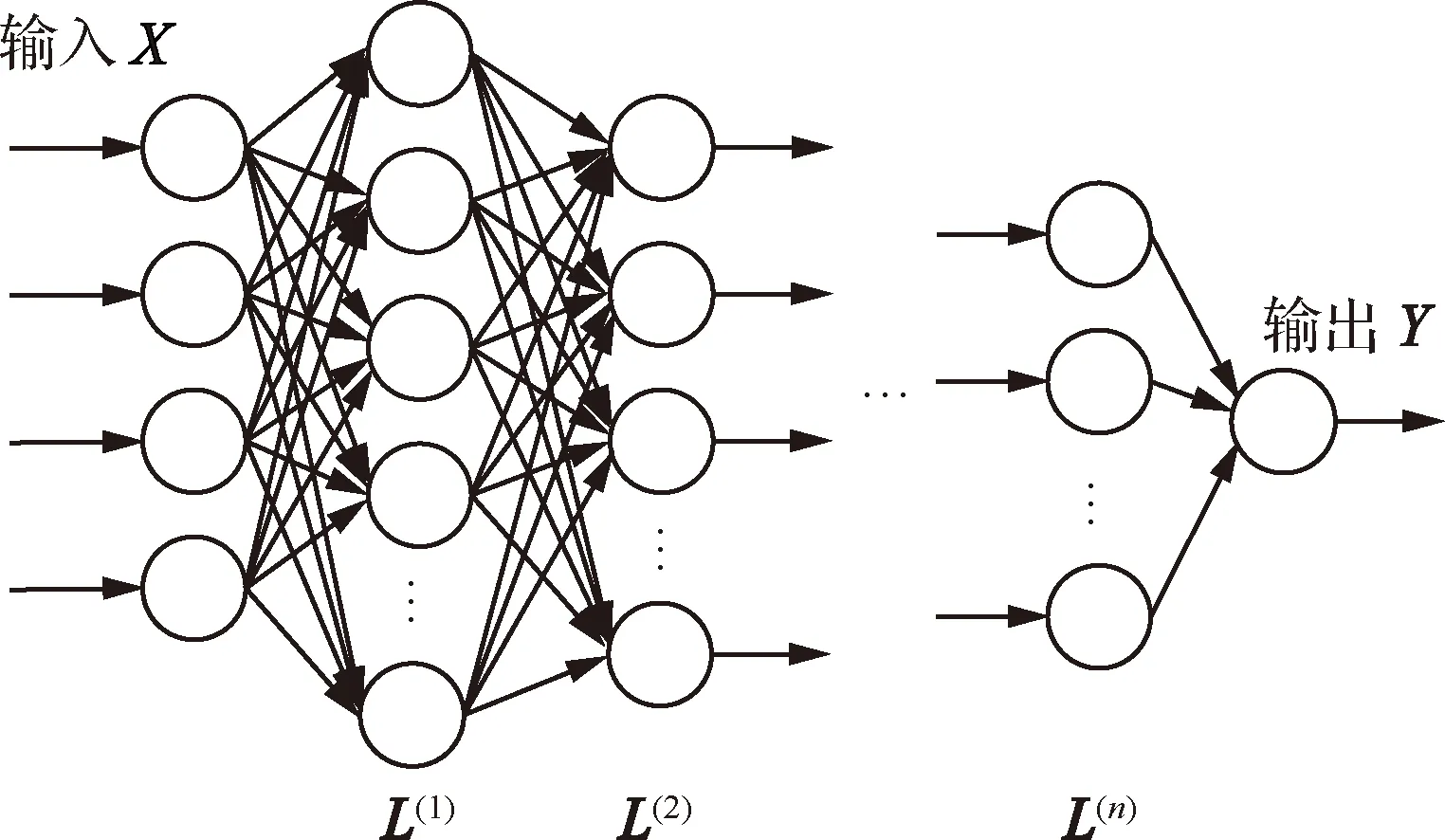
图8 堆栈式稀疏自编码器网络结构Fig.8 Structure of stacked sparse auto-encoder network

网络全局调优是一个有监督学习过程，将地空导弹发射区训练样本数据中的离轴角θ、目标高度H、目标速度V和航路捷径P组成输入变量矩阵，即X=[θ,H,V,P]T，发射区远界R作为输出矩阵，即Y=RT，通过误差反向传播算法中对深度网络权值进行全局调优，直至满足误差收敛条件或达到最大仿真步长，记录下所有训练好的网络参数，即实现了堆栈式稀疏自编码的整个训练过程。

4 仿真实验

本文以某导弹在尾追态势下阵地海拔高度为0～3 000 m、离轴角为[-60°,60°]、目标高度为3 000～20 000 m、目标速度为100～800 m/s、航路捷径为-30 000～30 000 m时的部分地空导弹发射区远界数据作为训练样本进行拟合，其中部分样本数据如表1所示。

(12)

式中:xmin为x(i)的最小值;xmax为x(i)的最大值，经过归一化处理的所有训练样本值被转化为[0,1]区间的无量纲数据。

本文在对仿真结果分析时所用到的一些指标及其具体定义为

1) 平方根均方误差RMSE

(13)

2) 平均绝对百分比误差MAPE

(14)

式中：y为理论输出值；y′为实际输出值；T为样本个数。

3) 超界(失界)大误差点数统计

对于地空导弹发射区远界而言，超界是指通过网络计算得到的实际拟合远界值比理论值大，相反地，失界是指通过网络计算得到的实际拟合远界值比理论值小。通过对超界和失界情况下大误差点的个数统计，可以最直观地得到发射区远界的整体拟合结果与发射区远界理论值的误差分布情况，分别选取误差值Error≥10%和≥20%两种条件为两个档次的大误差，统计这两种筛选条件下的误差点个数，可以从另一个角度对网络的拟合性能进行对比评估。

表1 部分地空导弹(SAM)发射区远界数据

Table 1 Far-field launching area data for partial Surface-to-Air Missile (SAM)

离轴角/(°)目标高度/m目标速度/(m·s-1)航路捷径/m发射区远界值/m-3011000500-6000100000-159000700 2200096381.9 153000300-600043000 4517500100-1000049854.1 4515000700 6000100000 459000700-22000100000 453000100 800031854.1-3017500300 2400058236 4513000400-2600090236 303000100-1400033236 451000300-600032381.9 1511000600 2000100000 6011000800 12000100000-3030400-800031527.8-151000600-800042854.1-4530200 1600023000 309000600 18000100000 6013000600 18000100000 015000600 24000100000 015000600 16000100000-1511000100 1200059618-6011000200-1400063763.9 6011000500 800090618-4520000500 2200058381.9 606000700-1200066527.8-3015000300-1000082618-1511000100 2200058763.9 156000200 400050618-453000400-400041618 1517500600 1600070381.9

4.1 不同层AE收敛速度对比

为进一步研究训练SSAE网络中不同AE的训练速度，本文使用双隐层SSAE网络的第1层与第2层AE迭代误差的收敛速度来研究不同层AE的收敛情况。

由图9看出，在对含两层隐层的SSAE训练时，第1层AE的迭代误差下降较为缓慢，而第2层 AE训练时由于使用第1层AE的隐层作为输入，训练时迭代误差下降较快，这说明堆栈式的网络构建策略在一定程度上可以提升网络训练的效率。

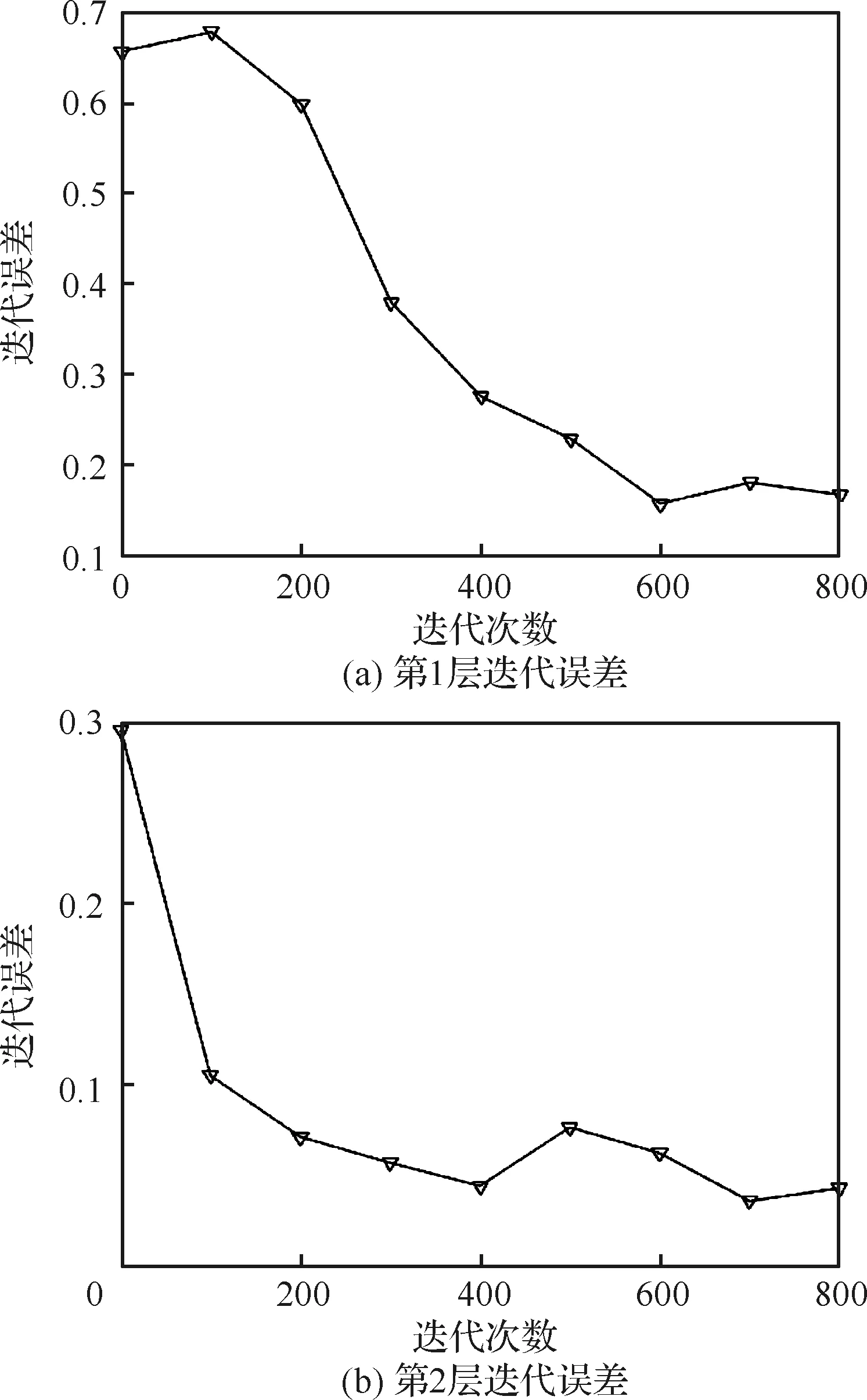
图9 第1层与第2层自编码器训练迭代误差Fig.9 Iteration error of the first and second layers of auto encoder

4.2 SSAE-DFN全局调优对拟合效果的影响

SSAE-DEN的训练过程分为预训练与全局调优两个部分，调优过程使用标签数据对网络进行全局调优，本文对单隐层、双隐层、三隐层与四隐层网络预训练与预训练加调优后的训练误差进行比较，研究预训练对训练效果的影响。

通过表2可以明显看出，仅预训练的网络相对调优后的网络存在较大误差，显然经过调优后的SSAE-DFN能更好的拟合发射区。说明预训练后再经过调优的网络能更好的拟合发射区远界。

表2 全局调优对SSAE-DFN网络训练误差的影响

Table 2 Influence of global optimizationon training error of SSAE-DFN network

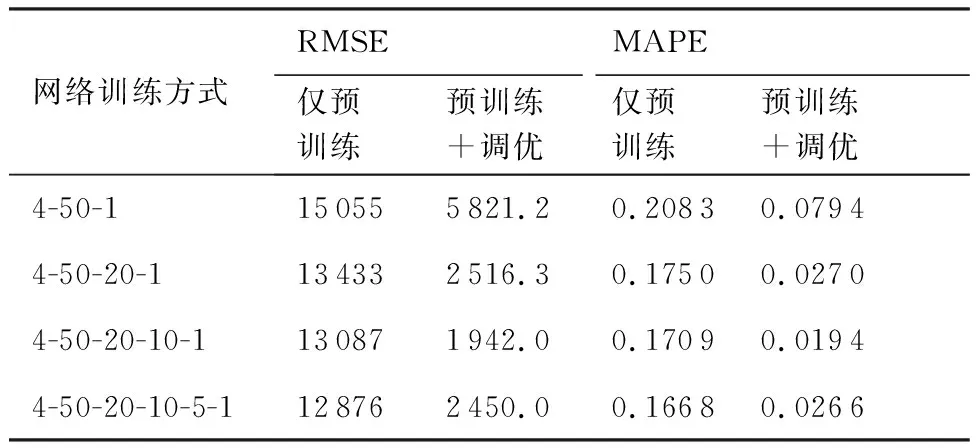
网络训练方式RMSEMAPE仅预训练预训练+调优仅预训练预训练+调优4-50-1150555821.20.20830.07944-50-20-1134332516.30.17500.02704-50-20-10-1130871942.00.17090.01944-50-20-10-5-1128762450.00.16680.0266

4.3 BP网络与SSAE-DFN性能对比

为了对比BP神经网络与本文设计的SSAE网络对地空导弹发射区拟合的效果，利用控制变量的思想，构建与多层神经网络具有相同隐层结构的堆栈式稀疏自编码器对地空导弹发射区远界样本进行训练，训练参数设定如表3所示。

表3 BP和SSAE网络训练参数Table 3 Training parameters of BP and SSAE network

4.3.1 BP网络与SSAE-DFN拟合效果对比

1) 评价指标结果对比

根据式(14)和式(15)定义的评价指标，所训练得出的BP网路和SSAE-DFN的各项评价指标如表4所示。

为了更直观地对比堆栈式稀疏自编码器与BP神经网络的拟合效果差异，可将SSAE-DFN与对应相同隐层结构的BP神经网络模型拟合结果的各项统计指标绘制在同一直方图中，可以得到如图10和图11所示。

表4 深度稀疏自编码器网络评价指标统计

Table 4 Statistics of sparse auto-encoder for deep network evaluation index

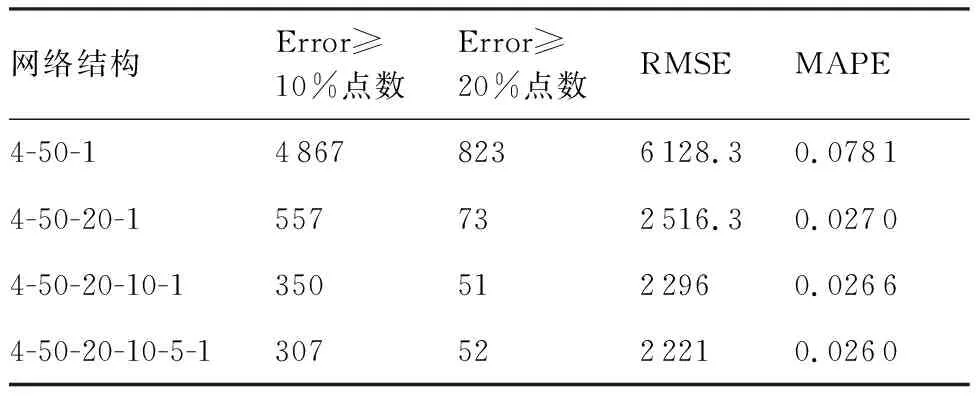
网络结构Error≥10%点数Error≥20%点数RMSEMAPE4-50-148678236128.30.07814-50-20-1557732516.30.02704-50-20-10-13505122960.02664-50-20-10-5-13075222210.0260

由图10(a)相对误差Error≥10%的点数对比统计结果可以看出，BP神经网络模型相对误差Error≥10%的点数随着网络隐层数的增加整体呈减少趋势，但当网络隐层数达到4层时相对误差Error≥10%的点数骤增，这说明BP算法不适用于深度网络的训练，出现了梯度弥散现象，之后的实验结果也表现出相同的现象。而堆栈式稀疏自编码器网络相对误差Error≥10%的点数随着网络深度的增加而减少，且整体Error≥10%的大误差点数相较于BP神经网络的拟合结果要少得多，误差Error≥10%的点数也没有出现剧增的现象，这说明SSAE-DFN可以有效地提升地空导弹发射区远界的拟合效果。

图10(b)为相对误差Error≥20%的点数对比统计结果，和图10(a)效果类似，可以明显看出SSAE-DFN的拟合效果在相较于相同隐层结构的BP神经网络模型有显著的提升，而且在网络深度到达一定程度后，相对误差Error≥20%的点数可以被控制在一个非常少的范围内，这可以使火控系统在实际应用中达到相当高的精度。

从图11(a)的结果来看，SSAE-DFN的RMSE值在相同隐层结构下对比BP神经网络要小一倍，整体随着隐层数的增加而下降。根据RMSE的定义可知RMSE的值用于表征拟合结果的整体离散程度，结果表明SSAE-DFN对地空导弹发射区远界的拟合结果大误差点数较少且整体误差较小。

由MAPE的计算方法可知，MAPE的值用于表征拟合结果的整体相对百分比误差。由图11(b) 直方图可以看出，SSAE-DFN的MAPE值随隐层数的增加而减小，整体比BP神经网络的值有较大程度的减少，BP神经网络的MAPE值最小为0.055 2，即整体误差为5.52%，而SSAE-DFN可以使地空导弹发射区远界拟合的MAPE值降至0.026 0，即整体误差为2.6%，相对于传统的BP神经网络拟合法性能提升多于一倍，这对于提升火控系统的整体性能具有重要意义。

2) 与理论值对比

图12为BP神经网络和SSAE-DFN拟合结果与理论值的整体对比图，图中蓝色的点是发射区远界理论值，橙色为两种网络的拟合结果。从结果中可以看出SSAE-DFN的拟合值与理论值更为接近，由此说明SSAE-DFN对地空导弹发射区的拟合效果更好。

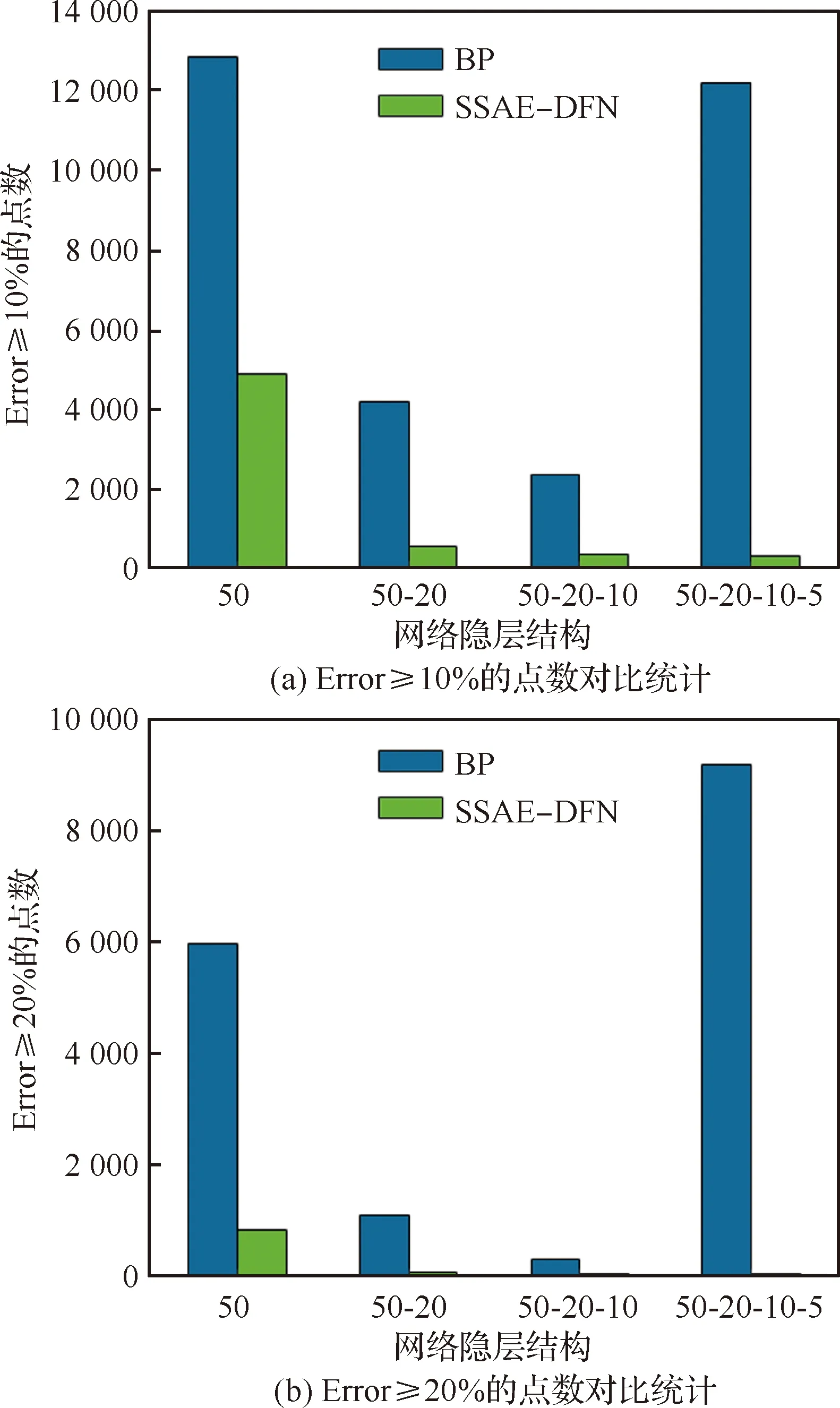
图10 堆栈式稀疏自编码器Error≥10%和Error≥20%的点数对比统计Fig.10 Comparison of stacked sparse auto-encoder Error≥10% and Error≥20% points

图11 堆栈式稀疏自编码器RMSE和MAPE对比统计Fig.11 Comparison of stacked sparse auto-encoder RMSE and MAPE

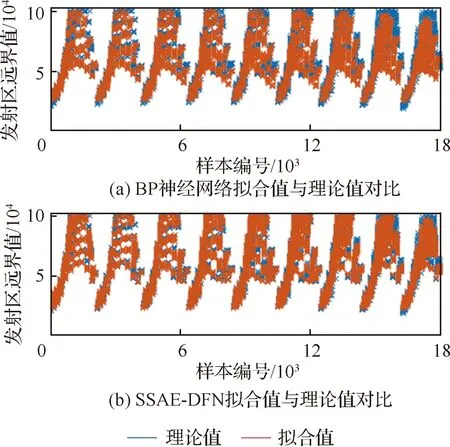
图12 发射区拟合值与理论值整体对比Fig.12 Comparison of overall fitted value of launch area with theoretical value

由于样本数较多，为了更显著地表现两种网络模型的拟合效果，选取部分发射区远界平面的拟合值和理论值进行绘图比较如图13所示，从图中可以明显看出，SSAE-DFN相较于BP神经网络，不仅拟合精度更高，而且能更好地表征出发射区的曲线特性。

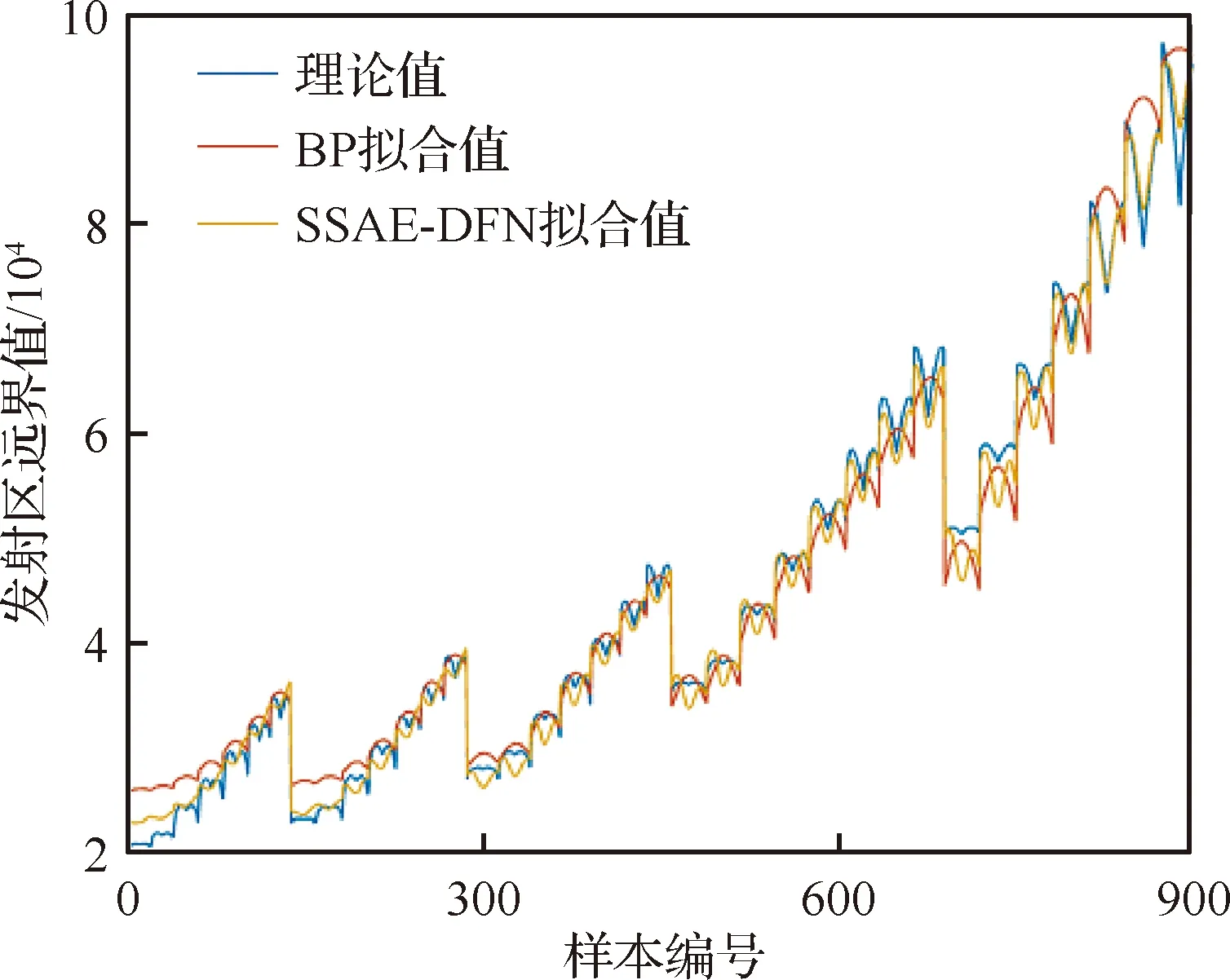
图13 发射区拟合值与理论值部分对比Fig.13 Comparison of fitted and theoretical values of launch area

4.3.2 BP网络与SSAE-DFN训练收敛速度对比

图14为两种网络模型在训练过程中迭代误差随迭代次数的变化趋势图，从该图中可以明显看出堆栈式稀疏自编码器网络比BP神经网络的迭代误差收敛速度快，且最终的迭代误差值更小，这说明SSAE-DFN模型相对于BP神经网络模型训练效率更高且训练效果更好。

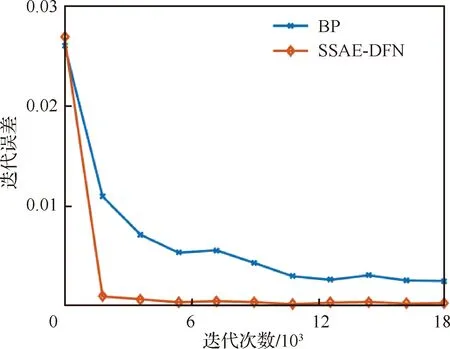
图14 两种网络模型迭代误差变化趋势Fig.14 Variation of iterative error in two network models

综合以上各项评价指标和对比图来看，深度SSAE-DFN模型相较于传统BP神经网络，不仅训练效率高，对标签化数据依赖低，而且可以有效提升地空导弹发射区远界的拟合精度，使拟合误差控制在一个较小的范围内，这充分说明深度学习算法模型在地空导弹火控发射区拟合问题中具有更为优秀的性能。

5 结 论

1) 采用SSAE-DFN模型对地空导弹发射区进行拟合，不仅有效地解决了多项式拟合法中地空导弹发射区工作式难以确定的问题，且相较于传统BP神经网络可以达到更高的发射区拟合精度，训练效率也更高。

2) SSAE-DFN模型相较于BP神经网络模型，对标签数据的依赖性比较低，有效解决了地空导弹发射区拟合中标签数据不易获取的难题，也节约了数据标注所需的资源和成本。

3) SSAE-DFN模型克服了深度BP网络易发生梯度弥散的缺陷，即使在隐层数较多时也能获得较好的训练结果。可以处理更复杂的地空导弹发射区拟合模型。

4) 对于SSAE-DFN等深度网络模型最优结构的确定方法，迄今为止仍未有可靠的理论支撑，在某些应用较为成熟的领域也仅有一些经验公式，但这些经验公式不具有普适性，如何找到合适的方法确定SSAE-DFN的最优结构是一项非常具有研究价值的课题，还需要未来进行更深层次的研究。