航天器介质盘环结构内带电特性三维仿真分析

原青云，王松，黄欣鑫

1. 陆军工程大学 电磁环境效应国家级重点实验室，石家庄 050003 2. 63618部队，库尔勒 841000

近年来，许多国家和研究机构投入了大量精力研究航天器的带电现象，包括表面带电[1-2]和介质内带电[3-4]。在地球同步轨道(Geostationary Earth Orbit，GEO)上，介质内带电被认为是导致航天器出现异常或故障的主要原因之一[5-7]。截至目前，还没有任何一个指导方针能够明确消除这种潜在威胁。如何评估产品初期的介质内带电水平。计算机仿真提供了切实可行的方法。目前已存在多款航天器表面充电仿真软件，比如欧空局(ESA)的SPIS(Spacecraft Plasma Interaction Software)软件[8]，美国NASA开发的航天器表面充电三维仿真软件NASCAP-2K(NASA Charging Analyzer Program)[9]和日本的MUSCAT(Multi-Utility Spacecraft Charging Analysis Tool)[10-11]。但是对于航天器内带电问题，由于涉及到介质内部电荷输运和电流平衡方程的复杂物理过程，目前还不存在任何介质内带电尤其是具备三维模拟能力的仿真工具能像SPIS在表面充电仿真领域那样得到广泛认可。

近年来，许多研究机构和学者进行了内带电仿真工具的研究。文献[12]指出最早的内带电仿真工具是著名学者Frederickson给出的NUMIT(NUMerical InTe-gration)，另一款较出名的仿真工具是欧空局的DICTAT(Dielectric Internal Charge Threat Analysis Tool)[13]，二者都是针对平板或圆柱等简单几何结构，且涉及到电荷输运模拟部分均采用经验拟合公式。黄建国和陈东[14-15]给出平板和圆柱结构的内带电一维模型，分析了介质厚度和接地方式对充电的最大电场强度的影响。虽然一维仿真能得到内带电的一般规律，但是为了发现实际复杂结构的充电危险点，三维仿真具有不可替代的作用，因为电场畸变常发生在复杂结构的边角和边沿。在20世纪70年代，研究者基于NASCAP构建了一种三维仿真模型[16]，用来动态仿真涂敷介质薄层的导体结构的充电过程，但仅是介质薄层结构。真正的内带电二维或三维仿真，只是在近几年才出现的，得益于电荷输运模拟软件Geant4在航天器内带电中的应用。张振龙等[17]给出了卫星部件内带电二维仿真结果；王松等[18]给出了内带电的三维仿真方案，对正面局部接地情况下的电路板内带电进行了仿真分析；王建昭等[19]基于Monte Carlo方法和有限元法提出了一种内带电模型对电阻接地状态下星用电路板的电场和电势分布情况进行了仿真。文献[20]指出基于Geant4开发出实用工具ATICS(Assessment Tool of Internal Charging for Satellite)来分析三维介质结构的电荷输运问题。总之，一维仿真终究只是得到内带电的一般规律，比如不同屏蔽厚度或接地方式对充电结果的影响，却不能考虑复杂的几何结构，从而容易忽视非规则接地条件下充电最严重的关键点；而已有的三维仿真没能合理评估局部特殊结构的充电水平，缺乏对局部电场畸变特征的探索研究。另外，对于介质内带电的屏蔽相关性，一些文献给出了一维情况下背面接地平板的研究结果[15,21]。实际上，屏蔽相关性随着介质结构或接地条件的变化会呈现不同形态，并且电导率的变化对于这种相关性尤为重要。通常建议介质内带电防护用的铝屏蔽厚度为3 mm，但是本文研究发现当本征电导率远小于辐射诱导电导率时，还不能满足。

为进一步揭示介质内带电关键充电点的特性，本文以航天器典型复杂介质结构——太阳帆板驱动机构(Solar Array Drive Mechanism, SADM)介质盘环为研究对象，选取该结构的典型部分进行三维仿真分析，探讨电场和电位分布特征，并得到不同屏蔽厚度下的充电规律，研究结果可为SADM抗内带电设计提供有益参考。

1 仿真方法

1.1 三维模拟方法

(1)

采用地球同步轨道恶劣条件下的电子通量模型Flumic3[23]，取能量大于2 MeV的电子通量为1×109m-2·s-1·sr-1，那么Qj和辐射剂量率D·分别为[22]

Qj=Qe/Δt，D·=De/Δt

(2)

式中：Qe和De分别为通过Geant4模拟得到的电荷沉积密度和辐射剂量；Δt=NG4/(feS)为完成该NG4个粒子入射的时间，NG4为模拟电子总数，S为粒子源有效截面积，fe为空间实际电子通量。

1.2 电导率模型

电导率是决定介质内带电的关键参数，一般需综合考虑温度、电场强度和辐射剂量率对电导率的影响，尤其是辐射剂量率，其对应的辐射诱导电导率往往能起主导作用。

将电导率σ分成两部分[24-25]：辐射诱导电导率σric及温度和电场共同作用下的电导率σET，则

σ=σric+σET

(3)

根据Fowler公式[26]，σric依赖于靶材料的D·，即

σric=kpD·α

(4)

式中：kp为由介质材料物理性质决定的常数；参量α代表介质内俘获能级分布情况，其取值范围一般为0.5≤α≤1.0。

另一方面，温度和电场强度对介质载流子浓度和迁移率产生影响。电导率随温度变化满足[27]

σET=A/kTexp(-EA/kT)

(5)

式中：A为介质材料物理性质决定的常数；k为玻尔兹曼常数；EA为材料的电导激活能；T为温度，K。同时考虑强电场效应，得到目前常用的电导率模型为[28]

σET=σT(2+cosh(βFE0.5/2kT))/3×2kT/

(eEδ)·sinh(eEδ/2kT)

(6)

式中：E为电场强度模值；σT为温度作用下的电导率；参数βF=(e3/πε)0.5，取决于材料的介电常数ε；e为电子电量；δ为电子在介质晶格间的跳跃距离，一般取值1 nm。

2 SADM盘环及其模型提取

SADM盘环体上下表面存在多条同心圆通道，且内部留有镂空的电缆通道，这使得SADM介质盘环成为航天器上典型的复杂介质结构。图1(a) 为3/4盘环结构示意图。不失一般性，选择具有代表性的局部结构进行分析，如图1(b)所示。该局部结构尺寸为14.0 mm×11.6 mm×13.2 mm，以坐标(0，2.6，0) mm为中心，关于z轴 对称。介质材料为聚酰亚胺，导体为银铜合金。介质和导体的边界视为接地。

在SADM的抗辐射加固设计中，选择恰当厚度的屏蔽层是一个关键问题。电荷输运模拟中，在介质结构上方设置一定厚度的屏蔽铝板。为了避免电荷输运模拟中的边界效应，将模型沿x、y轴方向适当扩展，Geant4输运模拟结构如图2所示，屏蔽铝板的下边缘到介质结构的上边缘距离为5 mm。因为航天器本体的遮挡作用，所以设置高能电子束垂直入射(满足指数分布)屏蔽铝板，电子穿过屏蔽层后沿多个方向入射到介质中。只对计算区域进行网格划分(网格空间步长为0.2 mm) 来得到Qe和De的三维分布，然后根据式(2)得到Qj和D·。

图1 SADM结构示意图Fig.1 Schematic for SADM structure

图2 Geant4电荷输运模拟Fig.2 Charge transportation simulation in Geant4

为了提高计算效率，针对不同厚度d的屏蔽铝板，设置不同的高能电子能谱的下限，而能量上限均为10 MeV。取能量下限Elow满足：

Rmax(Elow)=0.85d

(7)

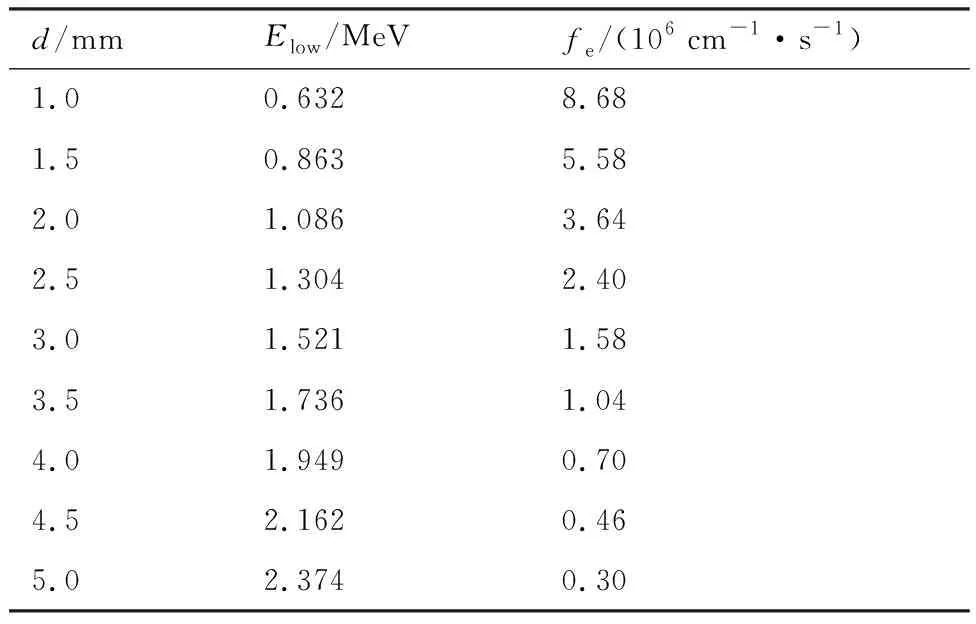
式中：Rmax为按照Weber经验公式得到的最大穿透深度[29]。根据Flumic3模型中电子通量的计算公式[23]，得到对应的电子通量fe，如表1所示。采用有限元法计算式(1)，计算中，σET及其相关参数的取值与文献[22]中给出的本征电导率拟合结果一致，根据文献[30]，σric计算中的kp和α分别取值为8.53×10-14Ω·m-1rad-1·s和0.713。

利用有限元法计算过程中，需要合理剖分网格以避免低估充电水平，作者前期研究了局部网格划分尺寸对非规则接地点处电场强度和电位的影响[18]，在此基础上，本文仿真结果表明电场强度峰值Emax出现在介质结构与导体接触的边界点上，如图3(该图为图1(b)的上半部分)所示，该点处在接地面的边缘，是内部沉积电荷最近的泄放点，由于介质和导体连接处局部电荷泄放路径的不规则性，使得该处存在电流密度汇集的“漏斗”效应，容易导致电场畸变放大。因此，需要加密此处的剖分网格来更好地刻画电场分布。选择切面x=-3 mm，以图3中圆圈标注的关键点处(-3，5.6，-1.8) mm附近的最大网格尺寸为变量，得到不同剖分细度下电位峰值和电场强度峰值，见表2。从表中看出，电场强度较电位变化更加显著。从物理机制角度分析，根据欧姆定理，电场强度与电流密度正相关，因而场强变化较电位更加剧烈；从算法角度来讲，这是因为场强是二次求解变量(电位U的负梯度)，对空间分辨率较U更敏感。因此在计算过程中，网格应充分细致以获得有效电场畸变结果。本文在设置关键充电点的加密网格尺寸为0.001 mm时得到的峰值电压(Umax)已达到收敛，Emax也达到107V/m 量级水平，因此，兼顾计算效率，设置该关键点处网格尺寸不超过0.001 mm(虽然不同网格尺寸下Emax数值有差别，但量级水平不变，所以认为该网格尺寸足以得到可靠结果)。

表1 不同屏蔽厚度对应的能量下限和电子通量

Table 1 Lower energy limit and flux of incident electrons corresponding to different shielding thicknesses

d/mmElow/MeVfe/(106 cm-1·s-1)1.00.6328.681.50.8635.582.01.0863.642.51.3042.403.01.5211.583.51.7361.044.01.9490.704.52.1620.465.02.3740.30

图3 关键点处的网格加密和对应的电场分布Fig.3 Mesh refinement and corresponding enlarged electric field on key charging point

表2 坐标点(-3，5.6，-1.8) mm处充电结果随最大网格尺寸的变化

Table 2 Variation of charging levels with the maximum mesh size at point (-3, 5.6, -1.8) mm

网格大小/mmUmax/VEmax/(MV·m)-10.1-1204.215.260.01-1209.8412.370.005-1210.1815.750.001-1210.5325.81

3 仿真结果及分析

3.1 Geant4模拟结果的统计均匀情况

在Geant4电荷输运模拟中，模拟电子总数NG4应足够大以满足统计均匀性要求。本文取值NG4=5×108个，其统计均匀效果如图4所示，图中数据取自屏蔽厚度为2 mm情况下坐标点(-3，5.6，-1.8) mm处的结果，可见已经达到统计均匀的要求。介质结构内部的电荷沉积率分布如图5所示(图中颜色越深表示电荷沉积率越大)。对照结构图1(b)，可见导体部位的电荷沉积现象最为显著，主要因为导体对电子的阻止本领显著大于聚酰亚胺。盘环表面的隆起结构中电荷沉积率较大，而导体屏蔽下的介质中电荷沉积率小得多。辐射剂量率具有类似的分布特征。

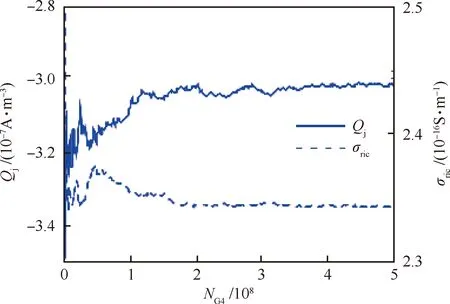
图4 Geant4模拟中Qj和σric随NG4变化的收敛情况Fig.4 Variation of convergence of Qj and σric with NG4 in Geant4 simulation

图5 电荷沉积率的三维分布切片图Fig.5 3-D distribution of cutting planes of charge deposition rate

3.2 电场强度和电位的三维分布

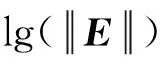
从矢量电场分布结果来看，传导电流密度从接地边界流向介质内部与内部沉积电子中和，内部电场方向朝向高能电子的入射边界。随着靠近接地边界，电位绝对值逐渐降低，即电场模值增大，此处是内带电的关键部位。从峰值电场强度方面考虑，SADM介质盘环内带电最严重部位位于盘环上层介质与金属导电环接触的上边沿。例如以上边沿的点(-3，5.6，4.6) mm为中点，沿z轴 上下各0.2 mm的线段上的电场分布如图8所示，电场峰值是特别集中的，远离峰值点0.1 mm 处的电场强度骤降一个数量级。注意到介质击穿放电往往正是由局部某个点出现强电场而发展到击穿放电的，因此在航天器SADM抗内带电设计中，应特别关注此类充电关键点。

图6 电位和电场强度的三维分布Fig.6 3-D distributions of potential and modulus of electric field strength

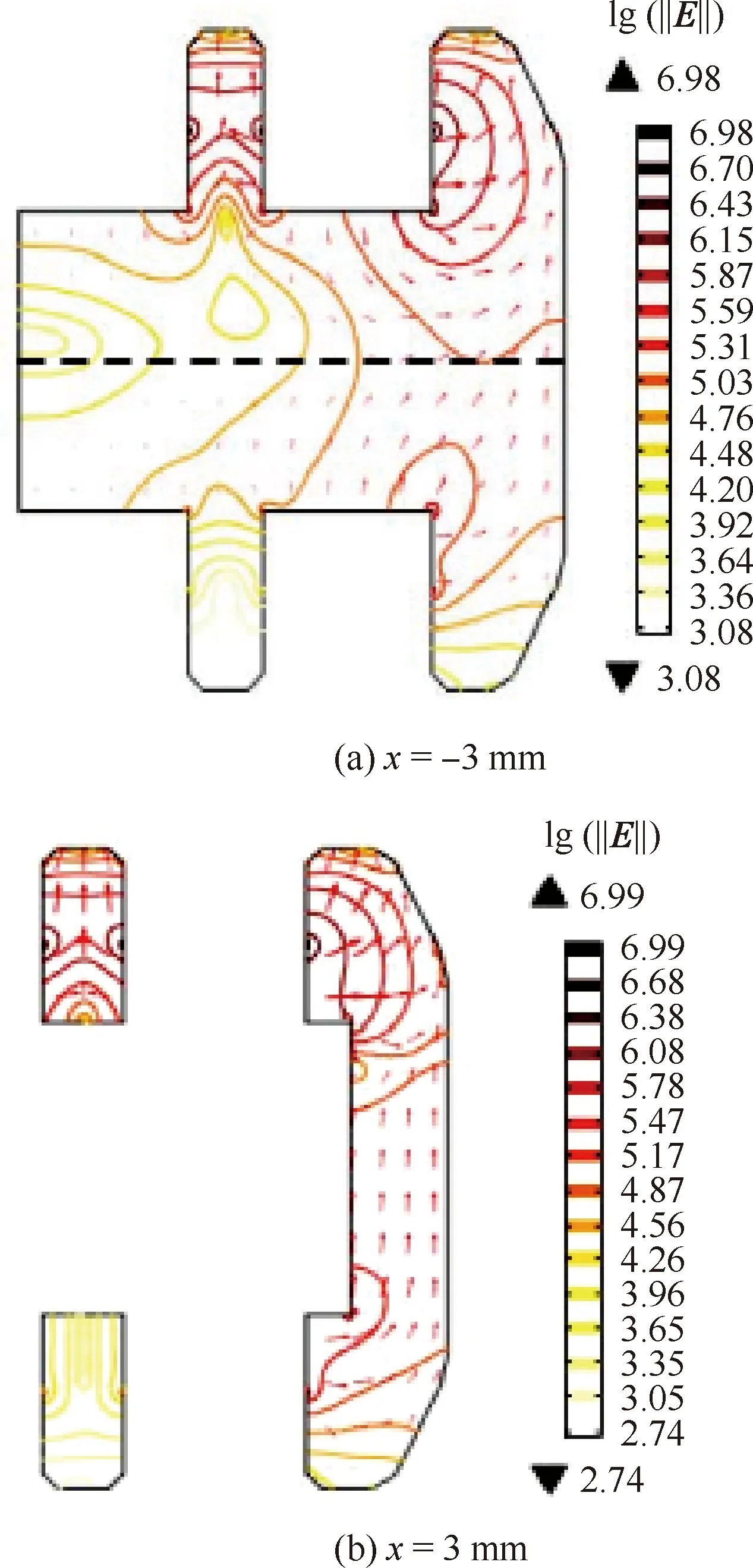
图7 切片x=-3 mm和x=3 mm上电场强度的分布Fig.7 Electric field distributions on cutting planes of x=-3 mm and x=3 mm

图8 场强峰值点及其附近的电场强度Fig.8 Electric field distribution around peak point

3.3 屏蔽厚度对充电结果的影响

按照表1列出的多种屏蔽厚度分别进行仿真计算，得到不同温度(考虑到航天器运行于轨道环境中，当经过阴影区和光照区时，会面临温度93～523 K的变化情况[31]，本文选取了183，263和343 K共3种温度)下图7(a)所示的截面内电位与电场峰值随屏蔽厚度的变化结果，如图9所示。图中电位图的纵坐标取反向，以方便考察电位幅度随屏蔽厚度的变化规律。显然，随着屏蔽厚度增大或温度升高，内带电得到缓解。其原因是增加屏蔽厚度使得电荷沉积率下降，而升温导致电导率升高，前者有效限制高能电子入射导致的介质内部电荷沉积，后者有助于加快电荷泄放速度，所以都会取得缓解内带电的效果。

值得注意的是，充电结果随屏蔽厚度增大的下降趋势在不同温度下的表现差异很大。考虑到内带电过程受Qj和σET、σric等关键参数的影响，为此将不同屏蔽厚度下的相关参数进行归一化，得到不同温度下归一化电荷沉积率和总电导率随屏蔽厚度的变化趋势如图10所示。

图9 3种不同温度下充电水平随屏蔽厚度的变化Fig.9 Variation of charging levels with shielding thickness at three different temperatures

图10 归一化电荷沉积率和总电导率随屏蔽厚度的变化Fig.10 Variation of charge deposition and total conductivity with shielding thickness in the normalized form

以1 mm屏蔽下点(-3，5.6，4.6)处Qj和σ(取值1.32×10-6A/m3和3.28×10-14S/m)为参照进行归一化，3种温度(183、263、343 K)由低到高对应的σET分别取值4.38×10-19、6.84×10-16和3.22×10-14S/m。从图10中容易看出Qj随屏蔽厚度增加的下降幅度较σ更大，所以屏蔽能够有效缓解内带电。然而，相对来讲，屏蔽效果随着温度降低有所减弱。分析原因：在较低温度下，σric是σ的主要组成部分，增大屏蔽厚度不仅降低Qj，而且造成σric显著下降(从图10可以看出来)，从而低温下屏蔽效果出现减弱现象，即使3 mm 屏蔽下也有可能达到107V/m量级的电场强度，只是需要更长的充电时间，即电导率越低，充电平衡时间越长。当温度为183 K时，充电平衡时间约为15 h。考虑到造成严重内带电的充电环境可能持续几天时间，所以低温下的航天器内带电危害不容低估。

4 结 论

本文实现了航天器SADM介质盘环复杂结构在不同屏蔽厚度下的内带电仿真分析。为提高电荷输运模拟效率，根据特定能量电子的穿透深度，提出了可以针对不同屏蔽厚度设置不同的电子能谱下限的模拟方法。通过仿真研究得出：

1) SADM盘环内带电最严重部位是盘环最外圈上层介质与金属导电环接触的上边沿；随屏蔽厚度增加和温度升高，内带电逐步减弱，该现象可通过对比归一化电荷沉积率和总电导率进行解释；值得注意的是，虽然增加屏蔽厚度可以减缓充电风险，但是随着温度降低，屏蔽效果会随之减弱。

2) 在GEO恶劣充电环境下，当温度低至183 K时，由于辐射诱导电导率成为总电导率的主导部分，从而增大屏蔽的同时也会降低介质电导率，导致即使3 mm铝屏蔽下仍出现接近107V/m 的场强峰值，存在介质击穿放电的可能性。