机器人自动换刀系统刀夹受力及排布

蒋君侠，朱文杰，朱伟东

浙江大学 机械工程学院，杭州 310027

飞机装配作为现代飞机制造过程中的重要环节极大地影响着飞机寿命[1]。传统飞机装配采用人工制孔和连接，制孔质量由工人的技术水平决定，存在制孔效率低、制孔质量差等缺陷，无法满足现代飞机装配高安全性和高可靠性的要求。与人工制孔操作相比，机器人制孔系统能加快制孔速度，提高装配质量，改善工作环境，在工程中应用的比例正变得越来越高，机器人制孔技术研究也成为当前飞机装配领域研究的热点[2-8]。

机器人制孔系统的架构是在六自由度工业机器人末端安装制孔末端执行器。工业机器人可在其工作范围内对制孔末端执行器进行空间定位，末端执行器则实现制孔操作，包括检测、压紧、钻孔和排屑等[9-14]。在实际加工中，往往存在不同孔径的加工孔、加工材料特性有差异、刀具存在磨损与破坏，这就需要频繁更换刀具。通过配置自动换刀系统，就可减少加工过程的非切削时间，以提高生产率、降低生产成本。目前最先进的机器人制孔系统有EI公司的TEDS和The Quadbots[15-16]和宝捷公司的RACe[17]。浙江大学等国内高校对机器人制孔系统进行了深入研究，实现了工程应用[18-19]。

自动换刀系统的工作效率对机器人制孔系统的总工作效率有着较大影响。目前国内外先进的机床刀库有：德国CHIRON公司的FZ08S，日本MAZAK公司的FH480，台湾吉辅的40CV立式刀库[20]。这些刀库均单独配备了换刀机械手，而机器人制孔系统可以通过机器人的运动配合完成换刀操作，刀夹设计结构截然不同，故机床刀库不适用于机器人制孔系统。

开发适用于机器人制孔系统的盘式刀库，首先要确定刀夹对刀具的夹持力，如果夹持力过小，会使刀具脱落；夹持力过大，会损伤刀具表面。其次要确定刀具进出刀夹过程中驱动力，如果驱动力过大，将产生碰撞、冲击而损坏刀夹；若驱动力过小，则刀具难以进出刀夹。最后就是要解决盘式刀库中刀具的分布问题。

本文针对刀夹稳定夹持力、换刀过程刀夹阻力和刀夹双环排布进行研究，阐述机器人自动换刀系统及自动换刀流程，计算刀夹稳定夹持力、换刀过程刀夹阻力，通过简化刀夹组件轮廓及惯量计算，对4种刀夹双环排布方案进行选优，最后给出了容量为24把刀具的盘式刀库设计实例。

1 机器人自动换刀系统

1.1 自动换刀系统及刀库

如图1所示，飞机壁板机器人制孔系统主要由飞机壁板、工业机器人、末端执行器、盘式刀库、试刀架、控制柜组成。其中机器人自动换刀系统主要由工业机器人、末端执行器、盘式刀库组成。机器人自动换刀系统通过机器人的运动配合完成换刀操作，由于机器人具有较高的重复定位精度和较强的空间运动能力，从而无需配置专门的换刀机械手，是一种较为新颖的换刀方式。

盘式刀库结构如图2所示，内部结构主要由刀夹组件、圆形刀盘、伺服电机及减速器组件、气缸组件、支撑架等组成，各结构的功能如下。

图1 飞机壁板机器人制孔系统Fig.1 Robotic drilling system for aircraft panel

图2 盘式刀库Fig.2 Disc-type cutter library

1) 刀夹组件：由刀具、刀夹、衬套、导向柱等组成，如图2所示。刀夹的3个接触面实现对刀具的夹紧、定位；调节螺钉作用是改变刀夹的开口大小，使刀夹能适应一定直径范围内的刀具；刀夹组件通过衬套与圆形刀盘连接；导向柱与衬套构成滑动副，在气缸推动下，上下运动。

2) 圆形刀盘：刀盘为圆形结构，盘上开有刀夹组件安装孔、刀具避让孔、刀盘安装孔等工艺孔。刀夹组件以一定规律分布在刀盘上。

3) 伺服电机及减速器组件：伺服电机驱动刀盘旋转一定角度，使目标刀夹组件运动至气缸推板的正上方，用于选刀操作。减速器可以降低转动惯量，能减小伺服电机所需的功率。

4) 气缸组件：由直线气缸、气缸安装座、推板等组成。在换刀指令的控制下，直线气缸通过推板推动刀夹组件沿着衬套上下移动。

5) 支撑架：用于安装支撑整个刀库结构。支撑架采用了镂空结构、筋板结构，在满足刚度和强度的要求下，尽可能减少结构的体积。

1.2 自动换刀流程

图3为自动换刀工位。图4为气缸将刀夹组件推出的原理图。

如图5所示,自动换刀流程可以概括为

1) 伺服电机驱动刀盘旋转，选择刀夹组件；接近传感器检测刀夹组件是否为空，若不为空，重新选择刀夹组件，若为空，气缸将刀夹组件推出。

图3 自动换刀工位Fig.3 Automatic tool changing station

图4 气缸将刀夹组件推出Fig.4 Pushing out cutter clamp assembly by air cylinder

图5 自动换刀流程Fig.5 Flowchart of automatic tool changing

2) 机器人将执行器移动到图3所示的自动换刀工位，执行器换下刀具。

3) 气缸驱动刀夹组件退回。

4) 伺服电机驱动刀盘旋转，选择刀夹组件；接近传感器检测刀夹组件是否为空，若为空，重新选择刀夹组件，若不为空，气缸将刀夹组件推出。

5) 机器人将执行器移动到图3所示的自动换刀工位，执行器换上刀具。

6) 气缸驱动刀夹组件退回。

2 刀夹夹持力及换刀阻力计算

2.1 夹持力

刀具在刀夹中的受力情况如图6所示。其中δ为支撑面的倾斜角，φ1为左右夹紧支撑面的弧度，φ2为定位支撑面的弧度；Ffi、FNi分别为支撑面对刀具的摩擦力、支持力，Ft为刀具对左侧刀夹的推力，Fk为弹簧推力，G为刀具重量。

假设刀夹3个支撑面提供的支撑力与其弧度成正比，列出刀具及刀夹的平衡方程：

(1)

式中：μ为摩擦系数；m为刀具质量；λ1和λ2为力臂长度。

考虑到零件的制造精度和装配误差，可能存在刀具仅由2个夹紧支撑面支撑的情况，此时令式(1)中φ2为0。同时为了确保夹持的稳定性，借鉴机器人二指夹的设计，考虑安全系数S，则刀夹所需夹持力为

(2)

刀夹通过杠杆结构将弹簧的推力转化为夹持力。计算所需弹簧推力

(3)

图6 刀具夹持受力分析Fig.6 Force analysis of cutter clamping

2.2 换刀阻力

2.2.1 换刀过程分析

如图7所示，刀夹夹口轮廓曲线abcd中ab为直线段，bc、cd分别为圆心在e点、f点的圆弧段。以刀夹转轴中心O为圆心，建立图7所示平面直角坐标系XOY。直线L为刀具进出刀夹的运动轨迹，g点为刀具轮廓的圆心。r1和r2分别为刀夹轮廓、刀具轮廓的半径，r3和r4分别为e、c两点距离刀夹转轴的距离，ym为直线L到原点距离。

刀具沿着直线L进、出刀夹互为相反过程，只需研究刀具进入刀夹过程，就可以得到整个进出过程的受力情况。刀具沿着L进入刀夹的过程，可以分为两个阶段。

第一阶段为刀具与bc段接触阶段：刀具轮廓与刀夹轮廓bc段相切，刀夹相对刀具滑动且绕O处的转轴旋转(详见图7)，通过杠杆机构压缩弹簧。第二阶段为刀具与c点接触阶段：刀具轮廓与刀夹轮廓的c点接触，刀夹相对刀具滑动且绕转轴旋转，继续压缩弹簧。上述两阶段刀具受到相切点处的摩檫力和正压力，刀夹受到压缩弹簧的回复力、相切点(或c点)处的摩擦力和正压力，忽略刀夹与转轴之间的摩擦力。

在相切点(或c点)处联立刀具轮廓与刀夹轮廓的几何方程得到刀具轮廓相切点处的圆周角α与刀夹转角θ函数关系；通过联立刀夹、刀具的静力平衡方程，得到相切点(或c点)处水平方向的换刀阻力Fm。

图7 刀夹夹口几何形状Fig.7 Geometric shape of clip mouth

2.2.2 刀具进入刀夹过程计算

1) 刀具与bc段接触阶段

首先分析刀具轮廓相切点处的圆周角α1与刀夹转角θ1的关系；接着推导刀具进入刀夹过程第一阶段的换刀阻力Fm1。

以刀夹转轴中心O为圆心，建立图8所示平面直角坐标系XOY，假设刀具轮廓的圆周角α1处与刀夹轮廓bc的圆周角γ+π处相切时，刀夹的转角为θ1。

刀夹旋转θ1后，刀夹轮廓bc部分的曲线方程为

(4)

式中：(xe0，ye0)、(xe，ye)分别为旋转前后圆心e点的坐标；tL、tH分别为旋转前b、c点对应的圆周角；t1为圆弧方程的参数；γ1+π为旋转前圆心e点对应的圆周角。

根据刀具轮廓与刀夹轮廓的相切关系、刀具入夹的运动轨迹，可求解刀具轮廓的曲线方程：

(5)

式中：(xg，yg)为刀具轮廓的圆心g点坐标；t2为圆弧方程参数。

图8 刀具与bc段接触时几何关系与受力分析Fig.8 Geometric relationship and force analysis when cutter contacts curve bc

在相切点处联立式(4)和式(5)，解得α1与θ1的函数关系：

(r1+r2)sinα1=-r3sin(γ1-θ1)+ym

(6)

令式(6)中θ1=θ1min=0°，得到刀具刚接触刀夹时，相切点的圆周角为

(7)

令式(7)中α1=α1max=tH-θ1-π，得到刀具与刀夹在c处相切时，刀夹的转角θ1max和刀具对应的圆周角α1max：

(8)

式中：A=xe0+(r1+r2)costH；B=-ye0- (r1+r2)sintH。

故α1的范围为[α1min,α1max]，θ1的取值范围为[0,θ1max]。

刀具入夹第1阶段的受力如图8所示，FN3、Ff3为切点处的正压力与摩擦力，Fk1为弹簧推力，Fm1为刀具入夹第1阶段的阻力,λ3、λ4为正压力、摩擦力的力臂长度。

根据距离公式、杠杆原理、胡克定理、摩擦定理可得

(9)

式中：λ2tanθ0为弹簧的预紧压缩量。

解得刀具入夹第1阶段的阻力Fm1：

(10)

式中：yg=-ym；xg=-(r1+r2)cosα1+xe0cosθ1+ye0sinθ1；λ4=r1+r3cos(θ1+α1-γ1)。

由式(10)可知Fm1为θ1、α1的函数，结合θ1与α1的关系式(6)以及α1min、α1max、θ1max，利用MATLAB可以得到Fm1与α1的函数曲线。

2) 刀具与c点接触阶段

当刀具与c点接触时，分析过程与刀具入夹第一阶段类似。刀夹转角为θ2时，有以下几何关系：

(11)

式中：A=sinα2；B=sinα1max；C=sin(γ2-θ2)；D=sin(γ2-θ1max)；(xh0，yh0)、(xh，yh)分别为旋转前后c点的坐标；γ2+π为旋转前c点对应的圆周角。

求解式(11)可得θ2与α2的函数关系：

r2(A-B)=xh0(E-F)+yh0(G-H)

(12)

式中：E=sinθ1max；F=sinθ2；G=cosθ2；H=cosθ1max。

令式(12)中θ2=0°，刀具刚好完全进入刀夹，解得α2max：

(13)

则α2的取值范围为[α1max,α2max]，θ2先变大后变小。

刀具入夹第2阶段的受力如图9所示，分析过程与第1阶段类似，直接给出结果：

Fm2=

(14)

图9 刀具与c点接触时几何关系与受力分析Fig.9 Geometric relationship and force analysis when cutter contacts point c

2.2.3 刀具退出刀夹过程计算

刀具进入、退出刀夹互为相反过程，可推得刀具退出刀夹的刀夹阻力：刀具与c点接触阶段的阻力Fm3，刀具与bc段接触阶段的阻力Fm4。

(15)

3 圆形刀盘上刀夹双环排布

3.1 刀夹排布方法

研究圆形刀盘上刀夹双环排布规律是为了在刀具数量一定的条件下，通过合理排布刀夹，使刀夹靠近刀盘中心和刀盘直径变小，从而实现减小刀盘总惯量的目标。

刀夹组件排布采用以下策略：

1) 等间隔角。刀夹间隔角相同可以简化选刀过程的控制。

2) 简化刀夹组件轮廓。用两段圆弧和两段切线构成的刀夹轮廓包络线代替刀夹轮廓，只要保证包络线不相交，就可确保刀夹之间不发生干涉。刀夹轮廓包络线的尺寸参数r1、r2、l1、ε，如图10 所示。

3) 简化刀夹组件惯量计算。将刀夹组件惯量等效转化为刀座侧、刀具侧两部分，中心分别位于包络轮廓大、小圆弧圆心处。

基于上述策略，采用 A、B、C、D这4种内外环包络轮廓相切的方案来研究圆形刀盘上的总惯量最小的刀夹排布规律，如图10所示。方案A采用内外环刀具侧朝外的双环排布；方案B采用内环刀具侧朝外，外环刀具侧朝里的双环排布；方案C采用内环刀具侧朝里，外环刀具侧朝外的双环排布；方案D采用内外环刀具侧朝里的双环排布。R1、R2分别为内、外环刀夹的排布半径，Rp、R0为刀盘及刀盘中心孔的半径，R1m、R2m分别为刀夹轮廓包络线大、小圆弧排布半径的最小值，β为刀夹间隔角。

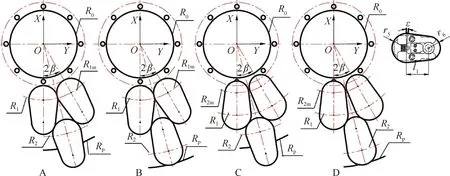
图10 刀夹组件轮廓简化及排布方法Fig.10 Profile simplification and layout method for cutter clamp assemblies

3.2 4种刀夹双环排布方案

4种排布方案计算原理相似，对方案A进行详细讨论，对其余3种方案直接给出结果。

1) 内外环刀具侧朝外的双环排布—方案A

内外环刀具侧朝外的双环排布方案中，内环分布半径R1=R1m，随着刀夹间隔角β的增大，内外环轮廓相切关系可分为3种。

第1种：内环小圆弧与外环大圆弧相切，β的范围为[β1,β2]。第2种：内环切线与外环大圆弧相切，β的范围为[β2,β3]。第3种：内环大圆弧与外环大圆弧相切，β的范围为 [β3,β4]。

β在[β1,β2]内，内外环轮廓相切如图11中1所示。根据几何关系，β1、β2、R2满足：

(16)

图11 刀夹组件双环排布方案AFig.11 Double-loop layout plan A of cutter clamp assemblies

式中：ω为线段eo、ef之间夹角。

求解式(16)得

(17)

式中：M=R1m+l1；N=r5+r6。

β在[β2,β3]内，如图11中2所示,外环刀夹轮廓的大圆弧圆心到切线ab的距离为r5，得

(18)

式中：ε1为切线ab与水平线的夹角。

求解式(18)可得

(19)

β在[β3,β4]内，内外环轮廓相切如图11中3所示。根据几何关系，β3、β4、R2满足：

(20)

求解式(20)得

(21)

2) 内环刀具侧朝外，外环刀具侧朝里的双环排布—方案B

如图12所示，直接给出结果，β满足：

(22)

当β在[β1,β2]、[β2,β3]、[β3,β4]、[β4,β5]时,R2分别满足：

(23)

图12 刀夹组件双环排布方案BFig.12 Double-loop layout plan B of cutter clamp assemblies

式中：M=R1m+l1；N=r5+r6。

3) 内环刀具侧朝里，外环刀具侧朝外的双环排布—方案C

如图13所示，直接给出结果，β满足：

(24)

当β在[β1,β2]、[β2,β3]时,R2分别满足：

(25)

式中：M=R2m+l1；N=2r5。

图13 刀夹组件双环排布方案CFig.13 Double-loop layout plan C of cutter clamp assemblies

4) 内外环刀具侧朝里的双环排布—方案D

如图14所示，直接给出结果，β满足：

图14 刀夹组件双环排布方案DFig.14 Double-loop layout plan D of cutter clamp assemblies

(26)

当β在[β1,β2]、[β2,β3]、[β3,β4]时,R2为

R2=

(27)

式中：M=R2m+l1；N=r5+r6。

3.3 4种排布方案惯量计算

刀盘整体的总惯量Jt由3部分组成：刀盘的惯量Jp，刀座侧的惯量Jdz，刀具侧的惯量Jd。根据图10可得到4种排布方案的刀盘总惯量。

(28)

式中：dt为衬套的直径；ρ为刀盘密度；h为刀盘厚度；J1、J2为刀座侧、刀具侧的惯量；m1、m2为刀座侧、刀具侧的质量；N为刀夹组件数量；l2、l3分别为内、外环刀具侧圆心与刀盘中心的距离，满足：

(29)

方案A中l2、l3均取加号；方案B中l2、l3分别取加号、减号；方案C中l2、l3分别取减号、加号；方案D中l2、l3均取减号。

刀夹间隔角β满足：

(30)

根据β的值和3.2节内容，代入式(28)可分别得到4种方案中N把刀夹组件排布的刀盘总惯量。利用MATLAB得到一定刀具数量范围内4种方案的折线图，进而选出较优的刀夹排布方案。

4 设计计算实例

4.1 刀夹设计参数计算

1) 夹持力

工程中的刀夹参数为：m=0.8 kg，θ=30°，μ=0.15，λ1=47 mm，λ2=25 mm，安全系数S=5，代入式(2)和式(3)得：夹持力FT=7.8 N、弹簧推力FK=14.8 N。

2) 换刀阻力

刀夹最大旋转角度θ不能超过10°。工程中刀夹参数为：r1=10 mm，r2=16 mm，r3=54.7 mm，tH=253°，xe0=-54.5 mm，ye0=-3.5 mm，ym=25 mm，λ2=25 mm，FK=14.8 N，μ=0.15，α0=7°，代入式(6)、式(7)、式(8)和式(10)得到

将α1max、θ1max、xc0=-54.42 mm、yc0=-13.06 mm 代入式(12)、式(13)和式(14)得

根据式(15)得

换刀阻力Fm由进刀阻力Fm1、Fm2和退刀阻力Fm3、Fm4组成，采用MATLAB数值方法，得到阻力Fm与α的函数曲线如图15示。图中P1、P2分别为Fm1与Fm2、Fm3与Fm4的临界点，对应刀具恰好与刀夹轮廓c点处相切。图中Q1、Q2分别对应进刀阻力、退刀阻力的最大点。上述分析计算的结论可以为控制机器人移动末端执行器进行换刀操作提供工艺参数。

图15 阻力Fm与α的函数关系曲线Fig.15 Function relation curves between Fm and α

4.2 刀夹排布方案选优

工程中刀盘及刀夹轮廓参数为：刀盘厚度h为15 mm，衬套直径dt为75 mm，刀盘密度ρ为7 850 kg/m3；刀座侧惯量J1为9.5 kg·cm2，质量m1为2.8 kg；刀具侧惯量J2为0.39 kg·cm2，质量m2为0.8 kg。其余参数见图16。

将4种方案的刀夹分布参数和刀盘参数代入式(28)中，利用MATLAB得到4种方案总惯量Jt与刀具数量N的折线图，见图17。可知，双环排布方案A即内外环刀具侧朝外的双环排布，能使刀盘的总惯量最小，为较优的双环排布方式。

图16 刀盘及刀夹轮廓参数Fig.16 Profile parameters of cutterhead and cutter clamp assemblies

图17 4种排布方案的结果和对比Fig.17 Results and comparisons of four layout plans

图18为采用方案A进行排布时，刀具数量为24的刀夹排布及刀盘结构结果。

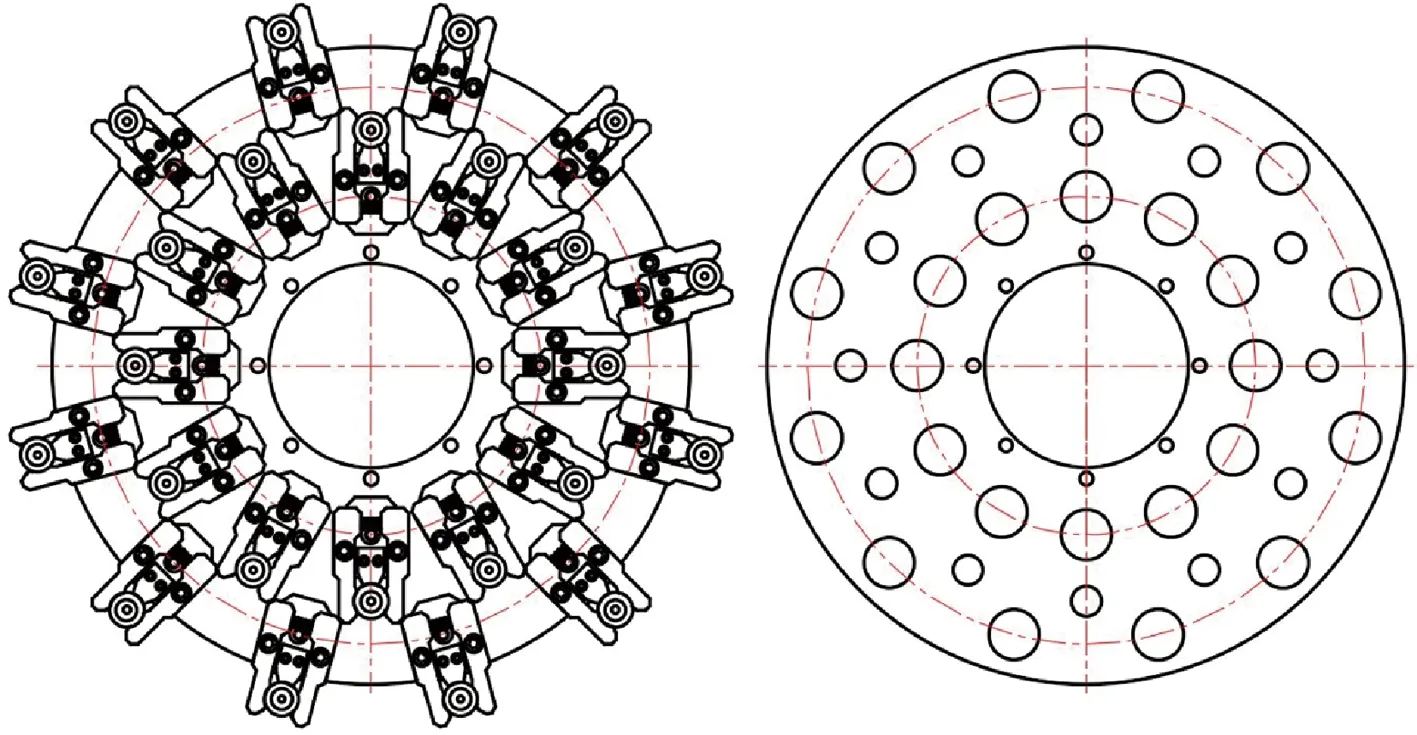
图18 刀夹排布及刀盘结构Fig.18 Distribution of cutter assemblies and structure of cutterhead

图19 机器人制孔系统及盘式刀库Fig.19 Robotic drilling system and disc-type cutter library

本文研究的盘式刀库经过设计、制造、装配和调试，已经成功应用到飞机壁板机器人制孔系统中(详见图19)，大大提高了飞机壁板的制孔效率。

5 结 论

1) 提出了一种新颖的机器人自动换刀方法，阐述了换刀原理和换刀流程。

2) 通过刀夹夹持受力分析，得到了刀夹稳定夹持所需的夹持力计算方法。

3) 针对刀具进出刀夹过程，通过几何和力学的综合分析并采用MATLAB数值仿真，得到了换刀全过程的刀夹阻力变化曲线。

4) 针对圆形刀盘上刀夹组件排布，通过以包络线来代替刀夹轮廓，以内外环包络轮廓相切和改变刀夹组件刀具侧朝向而产生多种排布方案，通过对比选优，得到了使总惯量最小的刀夹组件双环排布方式。

本研究中分析方法和计算方法，对设计自动换刀系统有着明显的指导作用。