基于新型电涡流阻尼器的大飞机垂尾装配界面精加工振动抑制

樊伟，郑联语,*，赵雄，杨毅青，刘新玉，杨森

1. 北京航空航天大学 机械工程及自动化学院，北京 100083 2. 上海飞机制造有限公司 航空制造技术研究所，上海 201324

垂尾装配结合面连接大飞机垂尾和后机身，属于设计分离面[1]。由于受零件制造误差、装配误差、测量误差及温度的影响，传统的垂尾装配结合面往往不能满足与后机身对接装配的精度要求[2-3]。因此，在对接装配前，需对垂尾装配结合面进行精加工处理。但由于每块装配界面是由钛合金制成的薄壁件，刚度较低，在加工时易产生严重的加工颤振和变形现象，导致其精加工质量无法控制。为保证及提高装配界面的精加工质量和效率，经研究发现振动控制技术是解决上述问题比较合适的方法途径。

按照工作机理，振动控制技术可分为阻尼、隔振和动力吸振方法[4]。按照动力驱动类型，上述各项方法又可细分为被动振动控制和主动振动控制。其中，阻尼技术主要是对金属表面进行阻尼处理来改变整个金属结构的阻尼系数以达到减振目的，如自由阻尼层处理[5]和约束阻尼层处理[6]。该技术虽然操作简单，但有时需将黏弹性阻尼材料粘贴在金属表面上，导致后期清洗工作比较费时繁琐。隔振主要是切断振动能量的传播路径，从而避免将振动能量传递到工件或设备上[7]，该技术目前还很少直接应用于薄壁件的数控加工中。而动力吸振器技术[8-12]主要是将一个或多个动力吸振器安装在振动物体上，通过调节吸振器的固有频率及阻尼特性来改变振动物体的振动状态以达到抑制振动的目的。其中，被动动力吸振器对于抑制稳定的窄频振动有效，但在切削过程中，随着材料去除，工件的固有频率在发生变化，当固有频率偏离最优同调频率[11]时，系统的减振功能会显著丧失。而主动动力吸振器可抑制宽频带振动，但其需附加大量的控制、驱动及在线监测等元器件而构成主动抑振系统，使得整个加工系统的复杂度提高、可靠性降低，工件的控制和加工生产成本也明显上升，因此该技术并不太适于数控加工中。据研究发现，电涡流阻尼器(Eddy Current Damper, ECD)是一种有效的解决上述问题的机电一体化被动减振装置[13]，可将振动机械能直接转化为热能而散失掉，这种不可逆的能量转化过程便达到了抑振目的。由于ECD具有阻尼系数易调节、机械结构简单、动态响应迅速、可靠性高、使用寿命长、维护方便等优点[14]，目前主要应用于楼宇及桥梁结构、高铁及汽车制动系统、航空航天精密仪器设备等领域的振动抑制中[15]，具有良好的应用前景。

国内外学者对ECD进行了一定研究，比较典型的研究有：Sodano等[16]针对悬臂梁结构件设计了一种ECD，并建立其理论模型，为估计悬臂梁受到的电磁阻尼力提供了理论支撑。为增加转子轴承系统的稳定性，刘淑莲和郑水英[17]提出了一种改进式被动ECD，其结构类似电磁轴承。当转子旋转时，在转子表面产生电磁阻尼，抑制转子振动，具有良好的在线消除轴承振动的效果。汪志昊等[18]设计了一种针对人行天桥减振的新型装配式竖向ECD，并提出了磁路优化布置及初步设计方法。针对同样的问题，Ao和Reyndds[19]采用一种新型涡流阻尼装置对传统动力吸振器进行改造来抑制人行天桥的振动，并采用有限元分析方法对新型吸振器进行了性能分析。结果表明在随机谐波激励信号作用下,该吸振器的阻尼效应得到了一定增强。Kienholz等[20]提出了一种面向航天飞机有效载荷隔振功能的ECD系统，该系统主要由一块铜导体板和两块永磁铁组成，通过导体在直流磁场中相对运动感应电涡流产生焦耳热而耗散振动能量。基于此，肖登红等[21]设计了一种可抑制航天器振动的筒形ECD，该阻尼器主要由两块导体板和一块永磁铁组成。通过数值仿真和实验验证，在外载荷激励下能够输出与仿真结果较为接近的阻尼力，进一步提高了该类型阻尼器的工作性能。此外，He等[22]还设计了一种被动ECD，主要由固定式永磁体和导电板组成，机械结构简单且具有较强的阻尼性能，可用于航天器的某些隔振系统中。Wang等[23]为解决大型传统调谐质量阻尼器(Tuned Mass Damper, TMD)的漏油和阻尼难调等问题，将ECD嵌入到TMD中重构了一种新型TMD，并对其进行了测试分析，结果表明该阻尼器对于结构振动控制是可行且可靠的。Lu等[24]也在传统TMD的基础上提出了一种非接触式电涡流TMD，并在一个五层钢架模型上对其进行了一系列振动台实验。结果表明在不同地震激励下，该TMD能有效降低钢架在竖直方向的振动响应。同理，Bae[25]和Yang[26]等也分别设计了相应的电涡流TMD，并分别将其应用在悬臂梁型和方框型结构件的振动抑制中，取得了较好效果。

总之，目前ECD技术在结构振动控制方面得到较广泛应用，但其在大型薄壁件的数控加工振动控制方面的应用还少有学者进行研究。基于此，在研究电涡流阻尼减振机理及装配界面精加工工艺特点的基础上，设计了一种用于抑制装配界面多模态振动的新型ECD(Novel Eddy Current Damper, NECD)。通过分析及验证表明该阻尼器能有效地解决装配界面的铣削颤振和根切问题，从而保证了装配界面的精加工质量和效率。

1 垂尾装配界面及其精加工系统

如图1(a)所示，民用大飞机垂尾装配结合面是平面多孔配合(2.5D制造特征)的复合结合面，由8块分布式装配界面组成(见图1(b))，其精加工工艺过程主要包括平面铣削和连接孔的镗削及钻削。如图1(c)和图1(d)所示，装配界面的精加工系统属于分体式加工系统[2-3]，主要由数控定位调姿系统、主动夹紧系统、数控系统、在机测量系统和外部激光跟踪仪测量系统等组成。其中，数控调姿定位系统用于垂尾大部件的定位和空间位姿调整；当定位和调姿完成后，在不破坏垂尾大部件气动外形及保证精加工过程稳定性的前提下，主动夹紧系统对其施加一定的夹紧力进行夹紧；当垂尾大部件完成装夹后，由CAD/CAM系统规划并生成数控指令并发送至数控系统、在机测量系统等，就可执行相应的操作。

装配界面主要由钛合金制成，属于难加工材料，整体结构刚度和导热系数较低，在铣削时易出现振动、变形、根切和刀具崩刃等现象，对装配界面的最终精加工质量和刀具的使用寿命造成了不可估量的影响。其传统加工方式如图2所示，在Z轴方向装配界面类似于底端固定，上端悬空的悬臂梁结构。在周期性铣削力作用下，其上端易产生较严重的颤振和让刀现象(见图2(c))。在X轴方向，刀具与装配界面的切入和切出区域，由于该处刚度较弱，对切削力比较敏感，刀具与其剧烈冲击易产生较严重的强迫颤振，致使其表面质量超差，甚至还会出现废品现象。因此，增加系统刚度和抑制铣削颤振是保证装配界面精加工质量的有效解决途径。

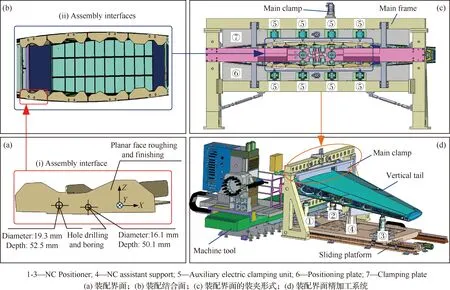
图1 装配界面及其精加工系统Fig.1 Assembly interfaces and their finish machining system

图2 装配界面传统精加工Fig.2 Traditional finish machining of assembly interface

2 NECD的设计及阻尼特性

2.1 NECD的设计及工作原理

如图3所示，设计的抑制装配界面多模态振动的NECD主要由静子和动子两部分组成。其中，定子包括导体管、导体盘和屏蔽罩等，而动子主要包括磁场激励源、磁靴、导向杆、弹性单元和执行末端等。其中，导体管和导体盘是产生电涡流的载体，其材料的电磁特性对阻尼器的阻尼性有重要影响，因此均采用电导率高且导热性好的黄铜制成；由于永磁体具有较高的矫顽力和磁能积，且不需要额外的供电设备和励磁绕组，因此选用具有优异磁力学性能的高磁性钕铁硼(NdFeB)永磁体作为磁场激励源；磁靴主要起传输永磁体磁场(称之为主磁场)、减小磁漏和提高主磁路磁通的作用，采用导磁率比较高的铁氧体制成；弹性单元通过执行末端对装配界面施加静刚度，防止装配界面在加工中产生弹性变形而造成根切现象，由具有一定弹性刚度的螺旋弹簧构成；屏蔽罩的主要作用是屏蔽主磁场，防止磁泄露对精加工系统中其他精密传感元器件或测量仪器造成磁干扰；永磁体与导体管之间的气隙用于保护永磁体，防止其与导体管碰撞而磨损，同时还能为导体管提供散热通道，但气隙磁场的厚度会对主磁场磁阻产生重要影响。为保证主磁场磁阻尽可能小，将气隙厚度控制在0.5～2 mm。

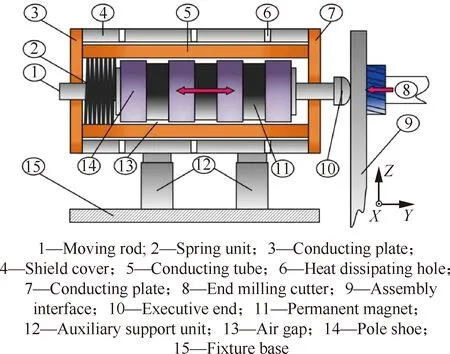
图3 NECD的机械结构Fig.3 Mechanical structure of NECD

另外，图4显示了永磁体的安装排列形式，其中永磁体与相邻的磁靴组合构成阻尼器的一个磁极。为增大磁靴处磁场的磁通量密度，永磁体均采用同极相对的排列安装方式[27]。其中，l为永磁铁的厚度；l1为磁靴的厚度；lp=l+l1为磁极的厚度；Rin、Rout和δ1分别为导体管的内径、外径和壁厚；R1、R2和δ2分别为导体盘的内径、外径和薄板厚度。

此外，执行末端固连于装配界面，这样可直接将装配界面的振动能量通过执行末端传递至NECD，使定子与动子发生相对运动而切割主磁场磁感线，使得导体部分的内部磁通量发生变化而在感应出电涡流。同时阻尼器的导体电阻在电涡流作用下便会产生焦耳热而耗散，这种不可逆的能量转化过程起到了抑制装配界面铣削颤振的作用。另外据洛伦兹定律知，由于电涡流和主磁场的相互作用，阻尼器还会产生一个抑制装配界面振动的电涡流阻尼力(简称阻尼力)，其也是表征NECD阻尼特性的一个重要工作性能指标。

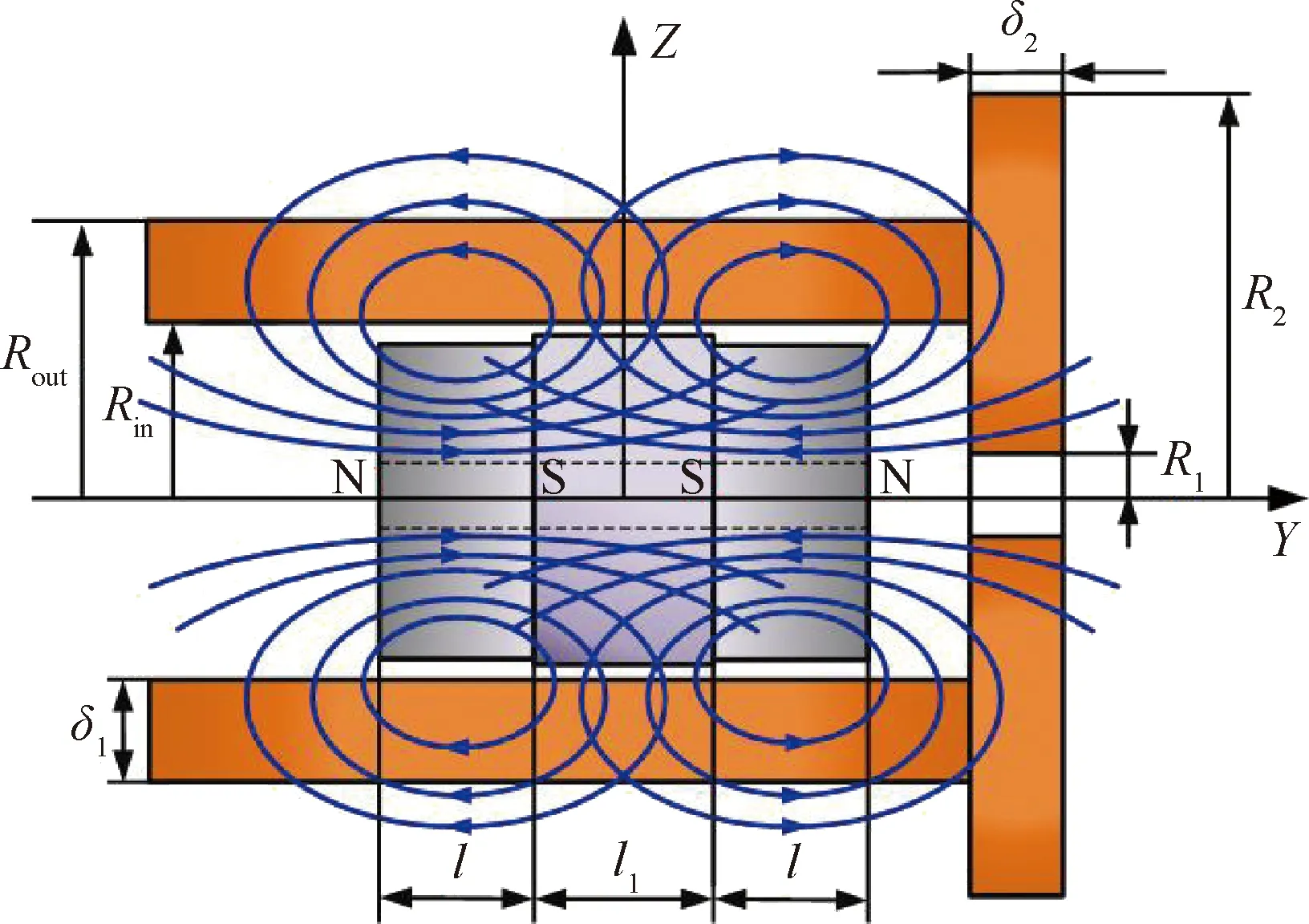
图4 NECD永磁体安装排列分布Fig.4 Distribution of permanent magnets for NECD

2.2 NECD的阻尼特性模型

如图3所示，由于NECD主要抑制装配界面法线方向的振动，故设定子与动子的相对运动速度为v，永磁体主磁场的磁感应强度矢量为B。即

v=0·i+vyj+0k

(1)

B=Bxi+Byj+Bzk

(2)

式中：i、j、k分别为沿X、Y、Z坐标方向的单位矢量;Bx、By、Bz分别为磁感应强度矢量B沿X、Y、Z坐标方向的分量。

根据电磁感应定律，由于阻尼器导体切割主磁场磁感线便会在其内部感应出电涡流，感应的电涡流密度J可表示为

J=σ(v×B)=σvy(Bzi-Bxk)

(3)

式中：σ为导体盘及导体管的导体电导率。

根据洛伦兹定律，NECD产生的电磁感应力(即阻尼力)fe可表示为

(4)

式中：V为导体管或导体盘的几何体积。

由于定子与动子的相对运动主要发生在导向杆轴向上且磁极中永磁体采用同极相对的安装方式，故只有主磁场的磁感应强度B的径向分量Br对阻尼力fe有效。据式(4)，阻尼力可表示为

(5)

由此可知，阻尼力fe与相对速度vy成线性负相关关系，其作用效果与黏性阻尼类似。C也可称为NECD的等效黏性阻尼系数。

另外，主磁场内任意点处的磁感应强度B可通过以下方法得到。如图5所示，坐标系O-XYZ为主磁场的全局坐标系(Global Coordinate System, GCS)，坐标系O1-X1Y1Z1为宽度为dy的无限小微分单元永磁体磁环的局部坐标系(Local Coordinate System, LCS)；点Q为主磁场内任一点，其在GCS中的坐标可记为(x,y,z)。y0为LCS到GCS的空间距离；rin、rout和l分别为永磁体的内径、外径和厚度。

由图5可知，有

r=r1-r2

(6)

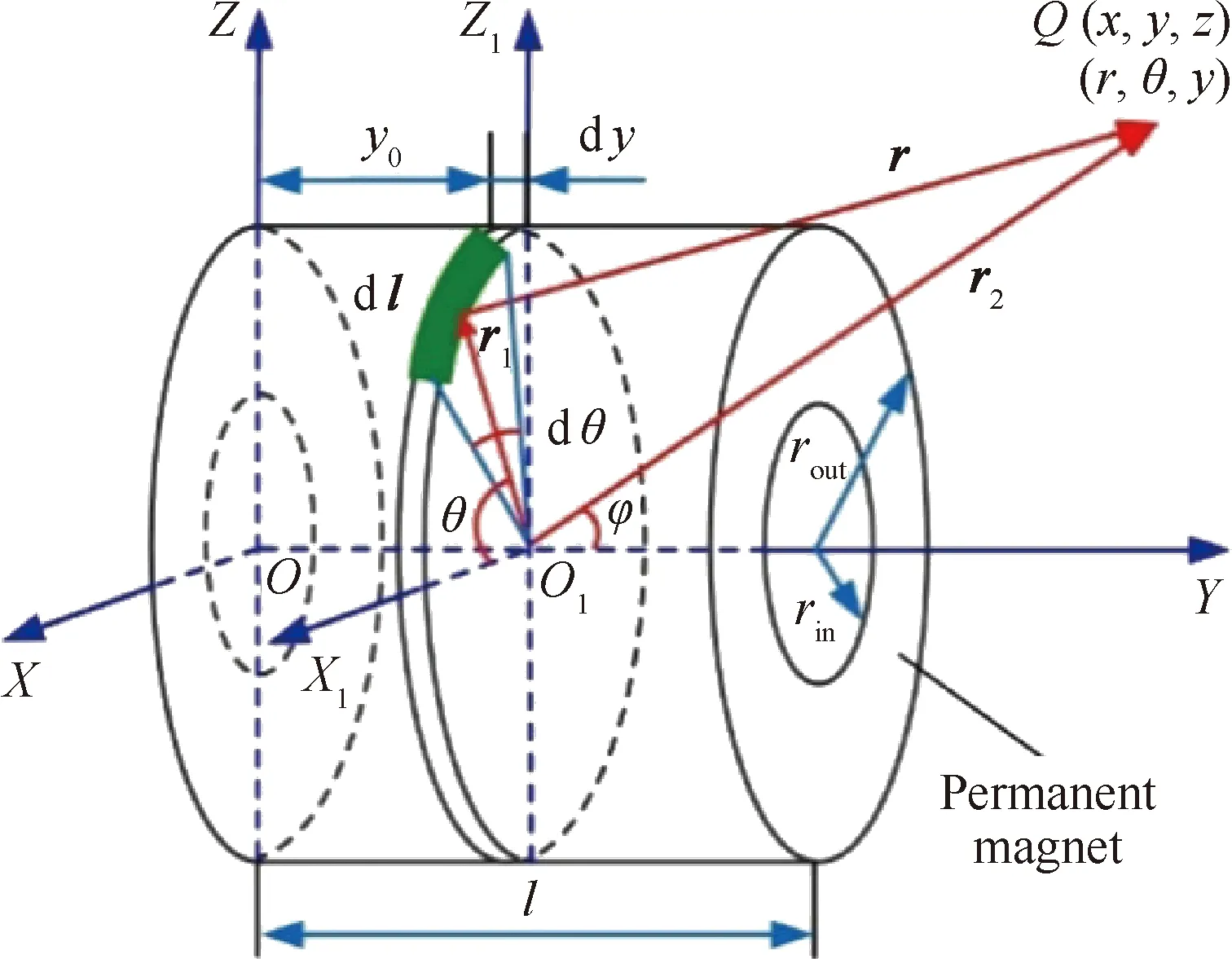
图5 主磁场空间任意点Q处的磁感应强度BFig.5 Magnetic flux density B of point Q in main magnetic field

式中：r1=routcosθi+y0j+routsinθk;r2=yj+zk。

因此，Q点处磁感应强度矢量BQ[13,16]可表示为

(7)

式中：P=-(y-y0)rcosθ;S=-r2+rzsinθ;

T=-r(y-y0)sinθ；μ0和M分别为永磁体的真空磁导率和磁化强度。且微分向量dl可表示为

dl=-routsinθdθi+0j+routcosθdθk

(8)

故磁感应强度矢量BQ在X、Y和Z三个坐标轴上的分量可表示为

(9)

(10)

(11)

因此，由式(7)、式(9)和式(11)可得到点Q处的径向磁通量密度矢量Br为

Br=BQx+BQz=BQxi+BQzk

(12)

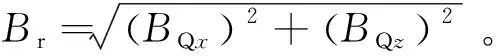
因此，考虑集肤效应的影响，由式(5)可知，因导体管产生动生电动势而感应的阻尼力fe1的大小可表示为

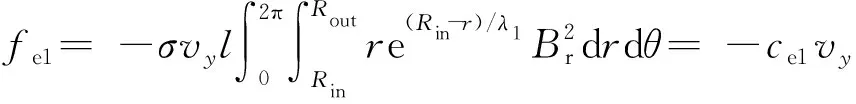
(13)

式中：λ1为导体管的集肤深度；则产生的等效阻尼系数ce1可表示为

(14)

同理，导体盘产生的阻尼力fe2的大小可表示为

(15)

式中：λ2为导体盘的集肤深度；则产生的等效阻尼系数ce2亦可表示为

(16)

由于NECD是由多个磁极组成的，则点Q处的径向磁通量密度为各个磁极磁通量密度的矢量和，故整个阻尼器产生的阻尼力fe的大小可表示为

vy=-cevy

(17)

式中：nm为阻尼器的磁极数。故整个阻尼器的等效阻尼系数ce可表示为

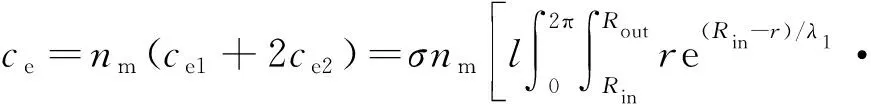
(18)

因此，可将式(17)和式(18)称之为NECD阻尼特性的数值模型。由此可知，NECD阻尼特性的影响因素主要包括相对速度vy和等效阻尼系数ce。而ce主要受阻尼器的材料和结构设计参数影响。因此，阻尼特性的影响因素主要为：磁极厚度lp、导体管厚度δ1、导体盘厚度δ2及其截面积s、磁极数nm等。以下利用数值计算和有限元仿真方法对上述各影响因素进行分析研究。

2.2.1 NECD阻尼特性随磁极厚度的变化规律

磁极由永磁体和磁靴构成，其厚度变化可分为两种情况：① 保持永磁体厚度l不变，变化磁靴厚度l1；② 保持l1不变，使l发生变化。

情况1如图6(a)所示，在一个完整的振动周期内，不难发现对任一l1，阻尼力fe都是先增大至峰值fe,max+后开始下降至反向峰值fe,max-，且有|fe,max-|<|fe,max+|。这是因为fe的随时间t变化趋势与vy基本一致，接近于简谐变化，且后半个振动周期内NECD接受的振动能量较弱于前半个周期。另外，对于不同的l1，随着其不断增大，fe开始随之增大，但当增至最大值(即l1=12 mm时)后其开始减小。这是因为当l1=6～12 mm时磁靴处的主磁场处于磁饱和状态，随着l1增加(即磁通截面积不断增加)，该处通过的磁通量会不断增大，使得fe与其对应的等效阻尼系数ce也随之逐渐增大。但随着磁通截面积的不断增大，受结构及材料限制，磁靴处的磁通量不会无限增大。故当l1>12 mm时，该处的磁通量密度B便开始减小，从而导致fe和ce也随之逐渐减小，如图6(b)所示。

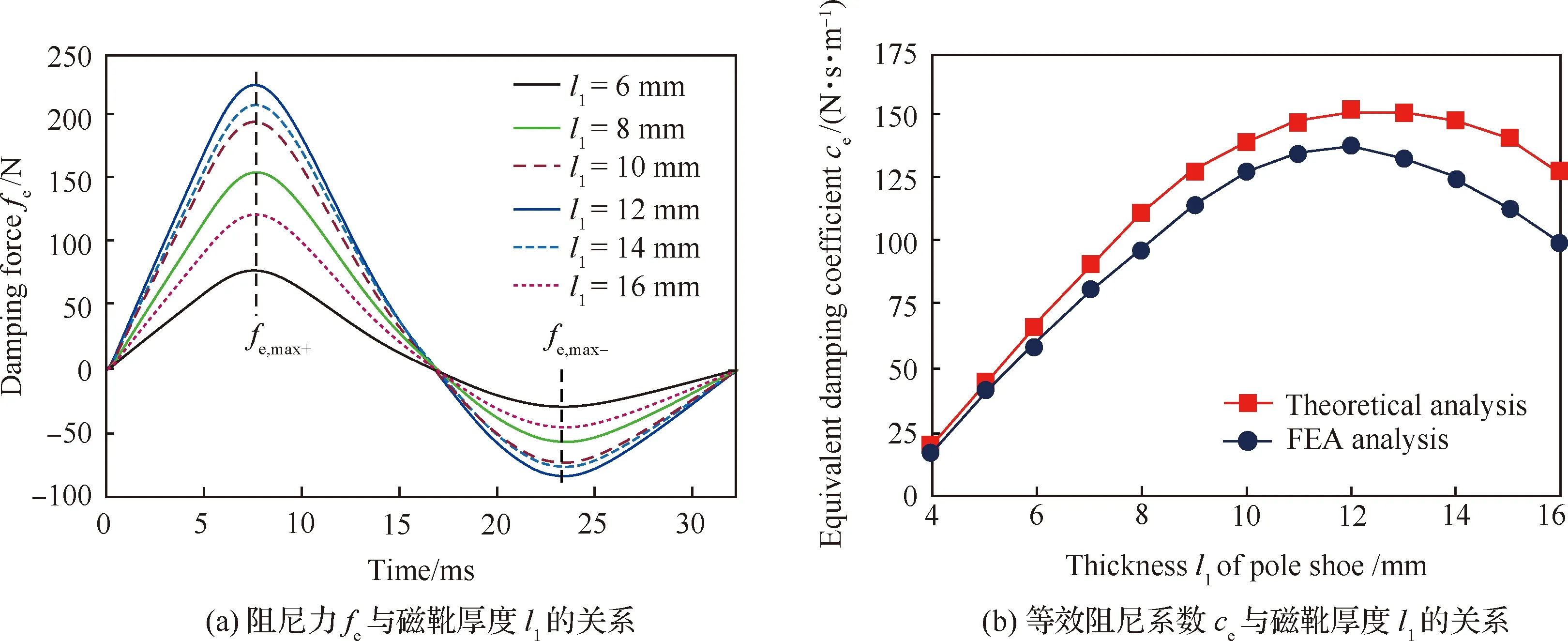
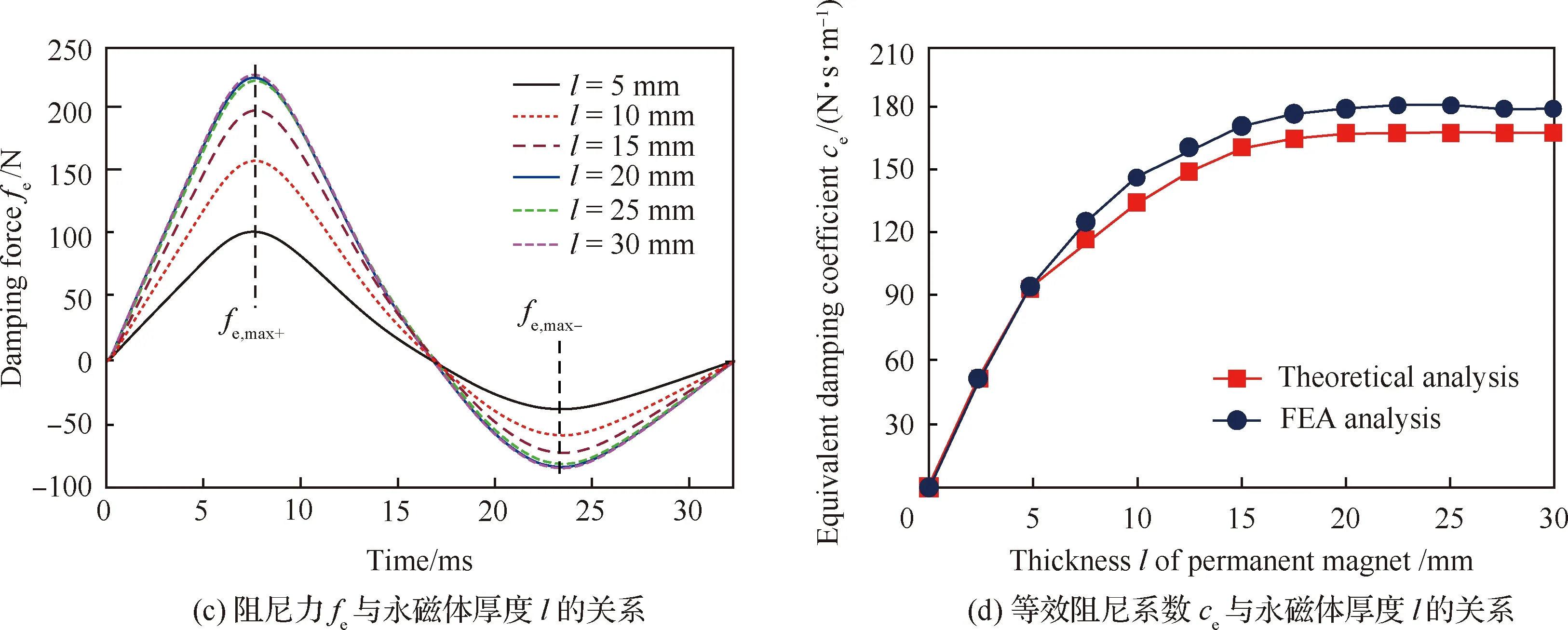
图6 NECD阻尼特性随磁极厚度的变化规律Fig.6 Variation of damping performance of NECD with thickness of magnet pole

情况2如图6(c)所示，分别改变l和l1的大小对NECD阻尼特性具有不同效果。随着l不断增加，fe随之逐渐增加，但其增量Δfe却逐渐减小。当l增至20 mm时，Δfe减小至零并保持动态不变，此时fe增至最大值。如图6(d)所示，与fe相对应的ce也有同样变化趋势。这是因为随着l增加，永磁体的磁动势也在不断增大，从而使得通过导体的磁通量密度B和由此感应的电涡流密度J也随之增大。但同时永磁体的磁阻及导体涡流区产生的电涡流磁场也在逐渐增强，并对B和J的增加起抵抗作用，致使NECD的阻尼特性不会随着l的增加而持续增强。

2.2.2 NECD阻尼特性随导体厚度的变化规律

对于导体管，改变其厚度δ1(即Rin保持不变，改变Rout的大小)，得到fe和ce随δ1的变化规律，如图7(a)和图7(b)所示。随着δ1增大，fe和ce皆是先增大至最大值(当δ1=4 mm时)后保持不变。因为随着δ1增大，导体管电涡流感应区域逐渐增大，电涡流效应也逐渐增强，使得fe和ce逐渐增大。但随着电涡流感应区域增大，对主磁场起抵抗和消磁作用的电涡流磁场也愈加增强，使得导管处主磁场的磁流通密度不断降低，致使fe和ce不能随着δ1而无限增大。同理，对于导体盘，改变其厚度δ2，也会得到类似的规律，如图7(c)所示。

图7 NECD阻尼特性随导体厚度的变化规律Fig.7 Variation of damping performance of NECD with thickness of conductor

另外，导体盘横截面积s对NECD阻尼效应也有明显影响。因此，改变s大小(即保持R1不变，改变R2的大小)，得到fe和ce随s的变化规律，如图7(d)所示。随着s增大，fe和ce也是先增大至最大值(当R2=50 mm时)后保持不变。通过比较发现，改变δ2比改变s对NECD的阻尼性能影响更大。因此，综合考虑阻尼性能、实际工作空间和制造成本等因素，设计NECD时应优先考虑改变δ2使其达到工作性能指标。

2.2.3 NECD阻尼特性随磁极对数的变化规律

在精加工中，要达到抑制装配界面铣削颤振的目的，不可避免地对NECD至少配置两对磁极。因此，分析磁极对数nm及布局方式对NECD阻尼性能优化具有重要意义。据研究[27]，为获得更好的NECD阻尼性能，其采用永磁体同极相对的排列布局方式，如图4所示。而NECD阻尼特性随磁极对数nm的变化规律如图8(a)和图8(b)所示。随着nm逐渐增加，fe和ce也逐渐增大至最大值(nm=6时)后并保持动态不变。因为随着nm增大，NECD电涡流感应区会逐渐增大，同时电涡流磁场的消磁效应及磁抗作用也会愈加增强，致使fe和与ce不能随之无限增大。

此外，工作温度对NECD的工作性能也有较大影响，当温度升高时阻尼器导体的电导率会下降，阻尼器产生的电涡流效应就会减弱。且当温度超至永磁体居里温度后，永磁体的性能会发生较大变化甚至会失效。因此，在屏蔽罩关键位置处设计并制造了散热孔，以便迅速有装配界面振动机械能转化的热量。总之，对比数值计算和有限元仿真方法的分析结果，两者之间具有较好的吻合度。因此，在分析NECD阻尼特性的同时也进一步验证了理论模型的正确性。因此，综合考虑以上分析结果、装配界面的精加工工艺特点及阻尼器有限的工作空间等因素，将NECD关键零组件的材料及几何参数可确定为如表1所示。

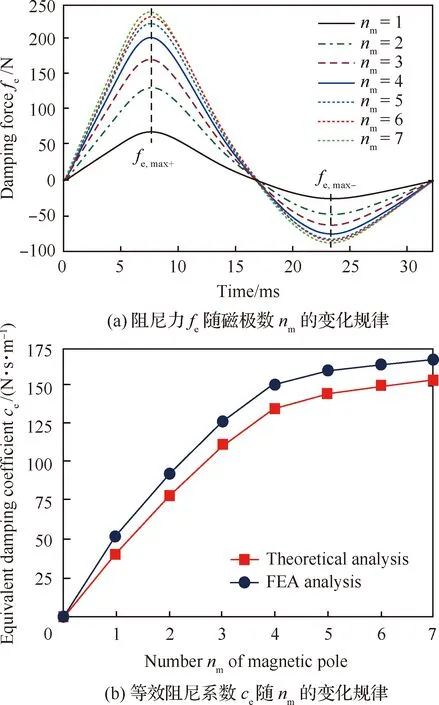
图8 NECD阻尼特性随磁极对数的变化规律Fig.8 Variation of damping performance of NECD with number of magnet pole

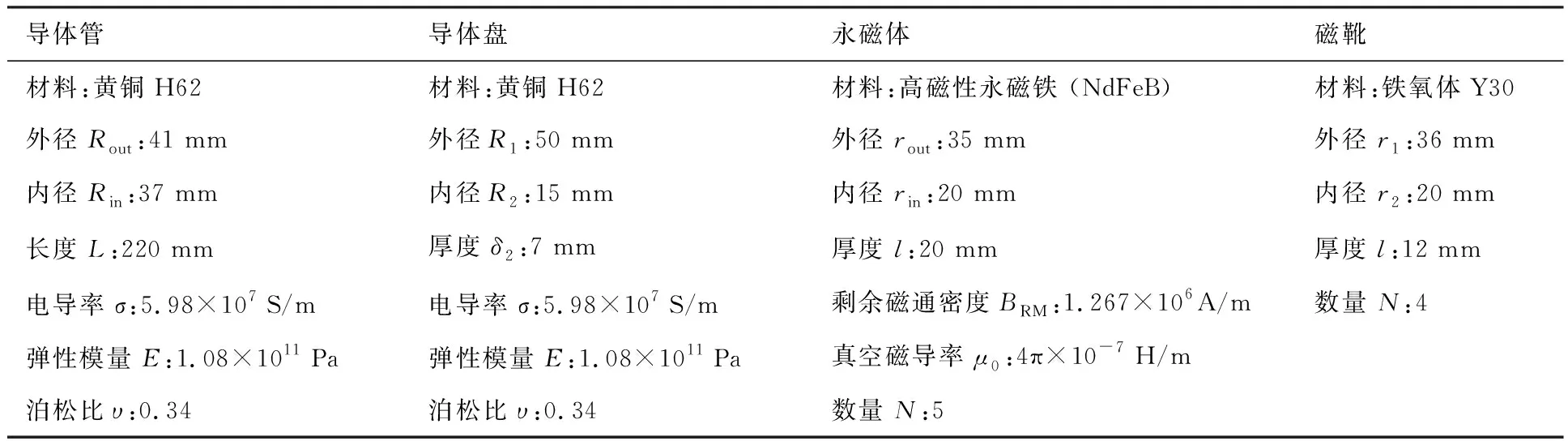
表1 NECD关键零组件的材料及几何设计参数Table 1 Material and geometric design parameters of key components of NECD

3 装配界面抑振系统的动力学分析

如图1(a)所示，对于每块装配界面，其左上及右上部刚性较弱，加工时振动和变形最为严重。为增加系统刚度，在每块装配界面的振动最严重的区域各配置一个NECD(该配置方案的可行性将在第4节进行详细论述)，从而构成装配界面的抑振系统(见图9(a))，而其对应的动力学模型如图9(b) 所示。其中，装配界面作为主系统，将其简化为质量块m0、弹簧单元k0及阻尼单元c0组成的单自由度系统连接到工装基座上；每个阻尼器作为一个子系统，将其简化为由弹簧单元k和阻尼单元c组成的单自由度系统连接到主系统的m0上。根据工艺知识，作用在主系统上的周期性铣削力可设为Fm=F0ejωt。因此，装配界面抑振系统在抑振方向上的运动微分方程可描述为

y0(t)=F0ejω t

(19)

式中：ω为铣削力的角频率；y0(t)为主系统在抑振方向的振动位移。

将式(19)进行傅里叶变换，可得到该系统的柔顺性函数为

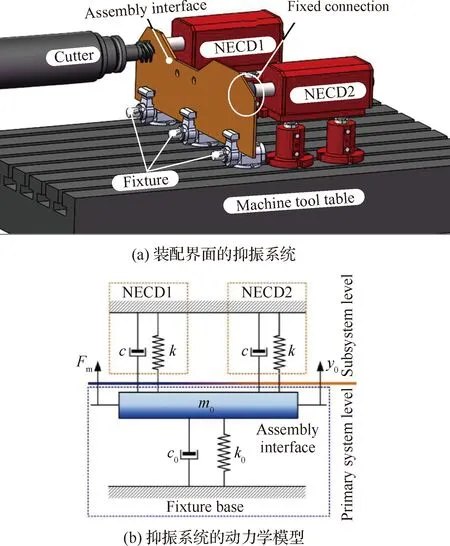
图9 装配界面的抑振系统及其动力学模型Fig.9 Vibration suppression system of assembly interface and dynamic model of vibration suppression system

H(ω)=y(ω)·F(ω)-1=[-ω2m0+

jω(c0+2c)+(k0+2k)]-1

(20)

根据周期性精加工铣削力的特点，则主系统的动态振动响应可表示为

y0(t)=Y0ejω t

(21)

将式(21)代入式(19)可得到

(22)

由于NECD有足够的设计刚度和稳定性，其自身产生的振动位移可忽略不计。对式(22)两边关于时间t求导，可得到定子与动子的相对速度vy为

(23)

另外，由于相对速度vy与装配界面的法向振动速度相等，故式(22)和式(23)也能表征在周期性铣削力作用下装配界面的动力学特性(即动态振动位移和速度响应)。因此，通过数值计算和有限元仿真分析，可得到NECD阻尼特性(fe和ce)与vy变化的规律，如图10所示。理论上NECD产生的阻尼力fe和相对速度vy呈线性相关关系。但有限元仿真结果显示fe不能随着vy而无限增大，当fe增至其最大值fe,max后便开始减小。经研究，随着vy增大，NECD的集肤效应越来越强，致使阻尼器导体的电导率下降，使得产生的电涡流密度J逐渐减弱，导致ce也随之逐渐减小，所以fe不会随着vy无限增大。另外，可将fe,max对应的vy称为NECD的临界速度vmax。因为当阻尼器工作速度超过vmax时，其阻尼特性会严重降低甚至会失效。因此，可将vmax和其对应的fe,max作为NECD的两大工作性能指标。

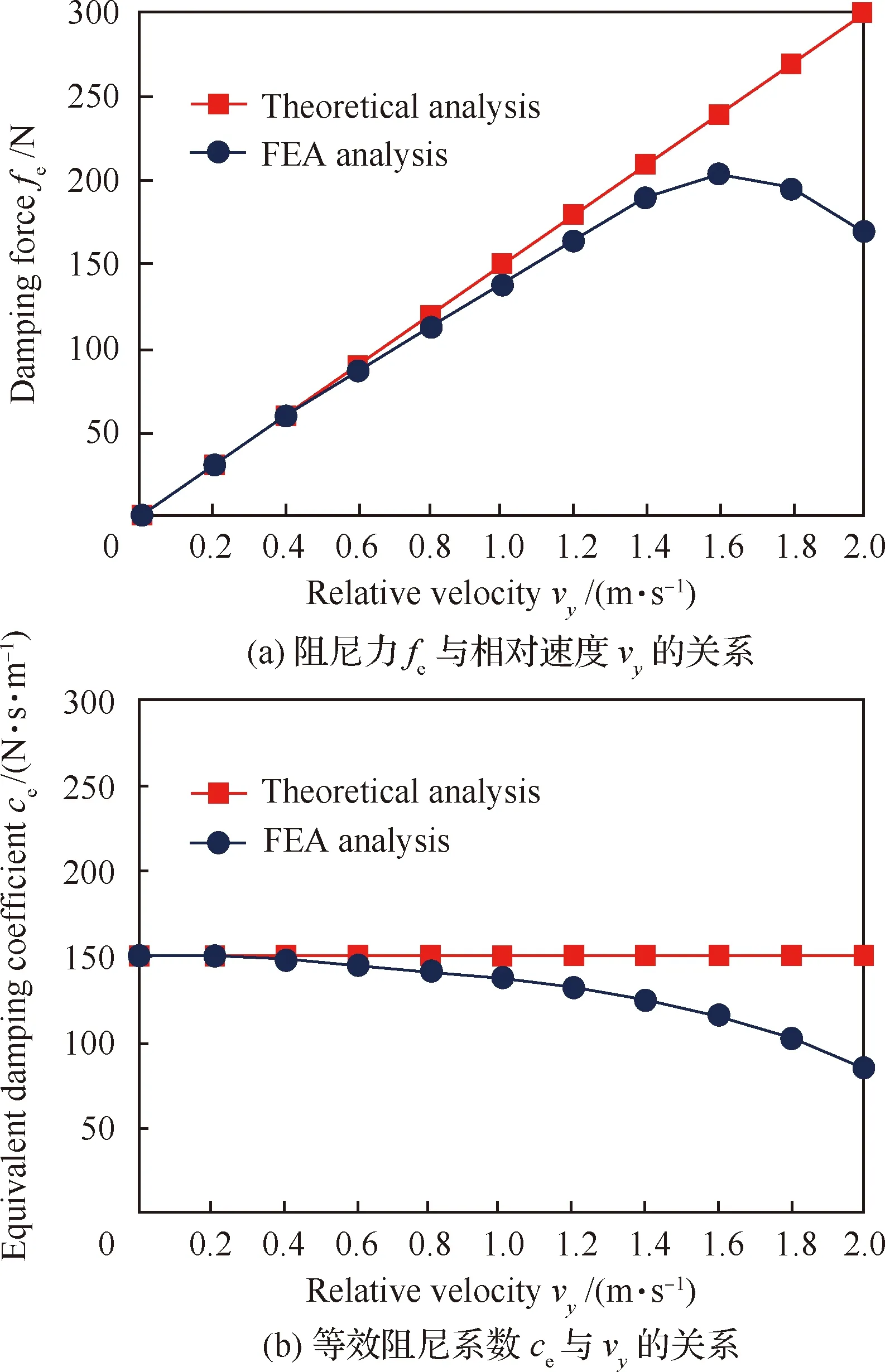
图10 NECD阻尼特性与相对速度的变化规律Fig.10 Variation of damping performance of NECD with relative velocity

4 实验验证及结果分析

如图1(b)所示，垂尾装配结合面是由8块边界约束条件和加工工况相同的装配界面构成。不失一般性，取其中一块装配界面作为样件并模拟其实际边界约束条件和加工工况，在三轴卧式复合机床上验证NECD对装配界面的抑振效果，整个实验设置如图11所示。

装配界面是由钛合金Ti6-Al4-V制成的薄壁工件，材料参数为：密度ρ=4.48×103kg/m3，剪切模量为G=4.17×1010Pa，弹性模量为E=1.14×1011Pa，泊松比为υ=0.33，其几何尺寸详见图12。其振动响应的数据处理系统主要由加速度计(型号INV9832-50、灵敏度为99.563 mV/g、频率范围为20 ～10 000 Hz)、数据采集仪(型号INV3062V2、24位网络式智能采集仪)和数据分析及处理系统(Coninv DASP-V11)等组成。

图11 装配界面的实验设置Fig.11 Experimental setup for assembly interface

如图11(d)所示，根据NECD的配置情况，可通过3种实验方案对装配界面进行动力学测试和切削实验验证，即:① NECD作用于装配界面；② 单 NECD作用于装配界面；③ 双NECD作用于装配界面。

4.1 动力学测试

如图12所示，采用锤击激励测试对装配界面进行动力学测试，将力锤作为激振源以施加脉冲信号，而加速计用于采集装配界面振动响应的加速度信号，经过数据分析及处理，可得到装配界面的动态振动特性。另外，在装配界面待加工表面上规划了49个分布点作为锤击激励点，同时将振动变形比较大的点1和7作为NECD与装配界面的固定连接点，将点4和5作为装配界面振动响应的拾取点(即加速度计的安装位置点)。

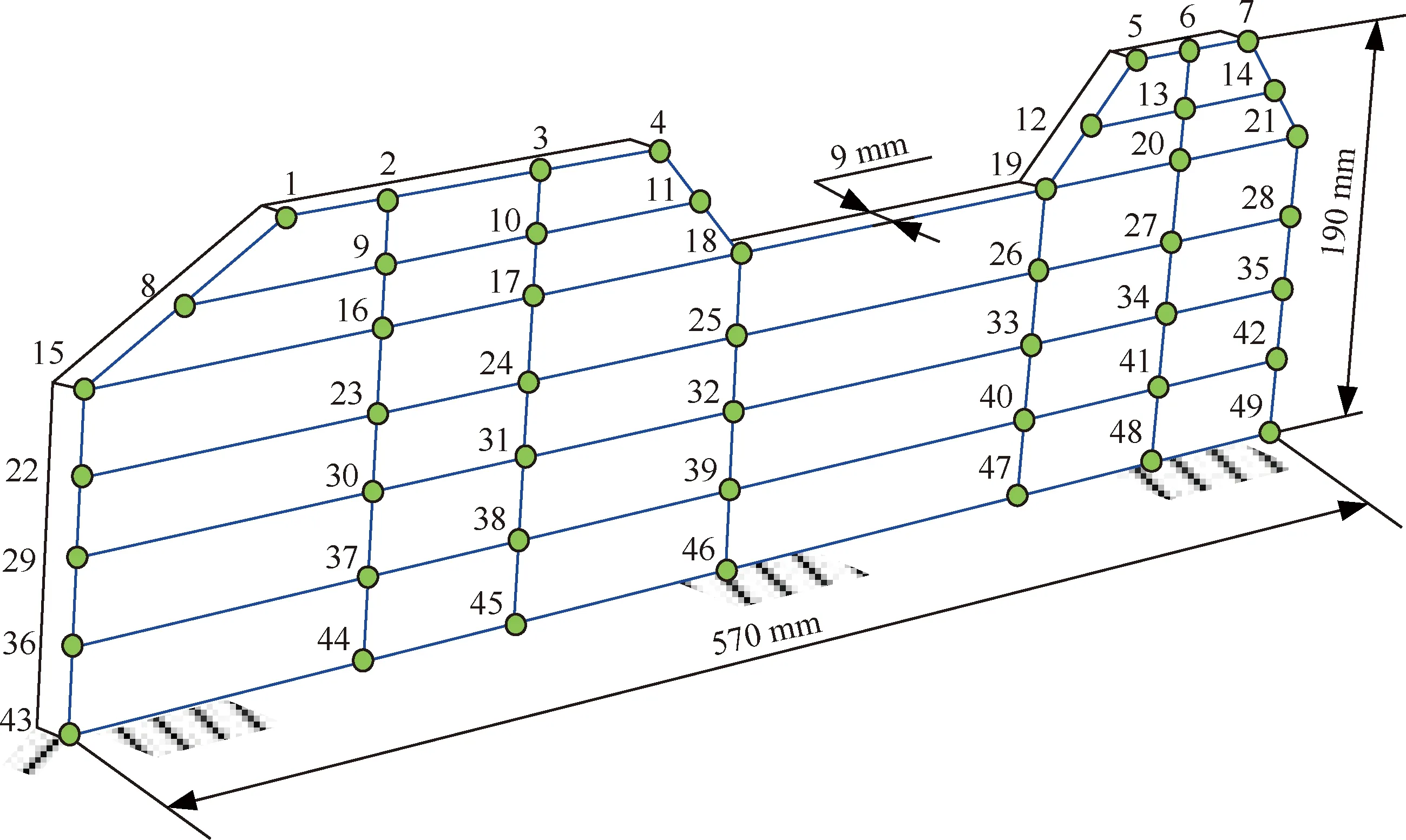
图12 装配界面的锤击测试Fig.12 Impact test for assembly interface

根据以上3种不同对装配界面进行测试，测得其频响函数(Frequency Response Function, FRF),如图13所示。在相同冲击条件下，单或双NECD作用时，装配界面的FRF幅值明显降低，且FRF频谱线也在逐渐变宽，说明在阻尼器作用下装配界面抑振系统的阻尼明显增加。

对测得的FRF进行动力学参数识别，结果如表2所示。其中，无NECD作用时装配界面的固有频率ωn为742.07 Hz，阻尼比ζ为2.4%及FRF幅值p为78.26 g/N。而在单或双NECD作用下，其ωn分别增至798.32 Hz、842.63 Hz；ζ升至4.1%、5.2%；p分别降至47.89 g/N、35.24 g/N。显然，单或双NECD作用时装配界面的阻尼比和等效刚度值明显增加，其中阻尼比最大能提高2.17倍，等效刚度最大能提高1.65倍，抑振效果明显提升。由于采用低频加工，固有频率的提高可有效避免装配界面精加工过程中的共振现象。另外，如图14所示，无NECD作用下，装配界面从外部冲击激励到稳定状态的衰减时间为0.26 s，而单和双NECD作用下，其衰减时间分别缩短为0.14 s和0.10 s，衰减速度分别提高了1.86倍和2.60倍。以上测试结果表明：NECD对于抑制装配界面因外部冲击而产生的自由振动具有较好的可行性和有效性，并且双NECD配置对装配界面的抑振效果更好。

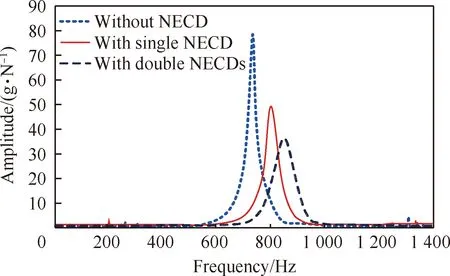
图13 装配界面的频响函数Fig.13 FRF of assembly interface

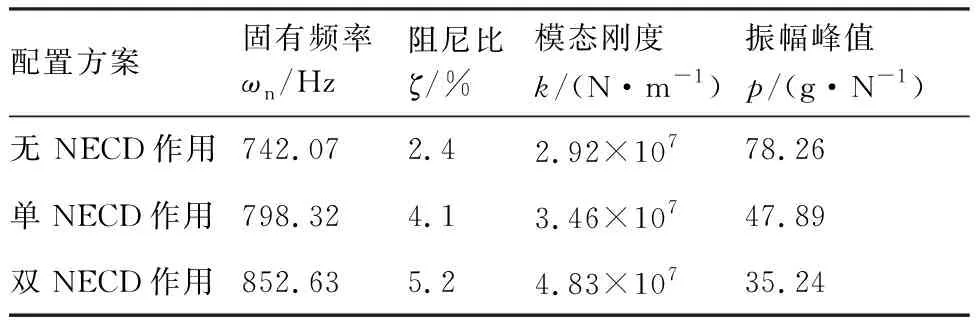
表2 辨识的装配界面模态参数Table 2 Identified modal parameters of assembly interface

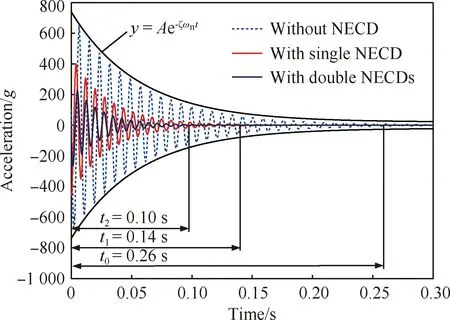
图14 不同NECD配置下装配界面的动态振动特性Fig.14 Dynamic vibration characteristics of assembly interface under different NECD configurations

4.2 切削实验

下面设计的一系列切削实验来进一步验证阻尼器的抑振性能。由于装配界面属于难加工材料，在精加工过程中易产生剧烈的强迫振动，使其加工质量难以控制，同时该过程还显著加剧了刀具磨损。为保证加工质量和减少刀具磨损，采用顺铣往复行切走刀的加工方式，且刀具选为直径为Φd=125 mm及齿数Zc=6的端铣刀。另外，由于过程阻尼的存在，加工稳定预测图对装配界面精加工过程稳定性预测作用不大。因此，基于加工工艺知识[28]和实际加工经验，将该实验的加工工艺参数确定为：主轴转速n=300 r/min，轴向切深ap=0.3 mm，径向切深ae=50 mm，切削进给速度vf=120 mm/min。同时，加速度计用来采集铣削过程中装配界面在产生的振动响应信号，如图15所示。

1) 如图15(a)所示，无阻尼器作用时装配界面振动的时域信号幅值达到了90g，有效值RMS为42.7g。对时域信号进行傅里叶变换得到相应的频域信号，从频谱图中可发现刀具切削频率的倍频fc=240 Hz处出现明显的颤振频率fcf=233.4 Hz，除此之外还出现了多个不同的振动频率，如fh=84.4, 157.2,326 Hz等。由此可判定装配界面的该铣削过程是非稳定的并伴随有强烈颤振发生。另外，从装配界面的表面加工质量也能直接验证这一现象，其表面粗糙度达25 μm，表面加工质量超差。

2) 如图15(b)所示，单NECD作用下装配界面的时域信号相比于无NECD作用时，其有效值RMS的幅值降低了近37.4%，且对应的频域信号中刀具切削频率的倍频fc=240 Hz和450 Hz占主导地位，无其他颤振或谐振频率，由此判定该铣削过程是稳定的。

3) 如图15(c)所示，相比于无或单NECD作用，双NECD作用下装配界面时域信号有效值RMS的幅值分别降低了64.4%和43.1%，表面加工质量达到了1.6 μm，且频域信号中占主导地位的只有频率fc=240 Hz和450 Hz。由此判定该铣削过程是稳定的。

值得指出的是，在NECD作用下，其与装配界面接触区域的刚度得到明显增强，可有效解决装配界面的根切问题。为验证该项性能，将图12中装配界面的点1～28(即变形比较敏感的点)作为铣削后的壁厚值测量点，并利用测厚仪对其进行测量，测量结果如图16所示。经分析知：无NECD作用时，装配界面的表面加工质量较差、回弹变形和根切现象较严重；单个NECD作用时，阻尼器与装配界面的作用区域加工质量较好且无明显回弹变形及根切现象，但非作用区域则与之相反，工件变形及根切现象较严重、加工质量较差；通过对比，双NECD作用下装配界面的加工质量更好，其壁厚能有效控制在11.676～11.739 mm 范围内，能较好地满足其加工质量技术要求。

在保证加工质量的前提下，双NECD配置还可进步优化装配界面的精加工工艺参数。经分析，工艺参数轴向切深ap和主轴转速n是装配界面铣削振动的主要影响因素。为此，有如下情况:

情况1双NECD作用下，其他加工工艺参数不变，即n=300 r/min，ae=50 mm，vf=120 mm/min，改变ap的大小(ap=1.0, 2.0,2.5 mm)对装配界面进行切削实验，得到的装配界面振动响应的时域和频域信号如图17所示。当ap=1.0,2.0 mm 时，振动响应的时域信号比较平稳，而对应的频域信号f=240 Hz和450 Hz 处的刀具切削频率倍频占主导地位，无其他颤振频率存在，表明该铣削过程是稳定的。从加工后的工件表面质量也能验证这一点，其表面粗糙度均不超过3.2 μm，满足技术要求。但当ap=2.5 mm时，装配界面振动响应的时域信号开始出现紊乱，在对应的频域信号中出现了明显的颤振信号f=137 Hz，且切削后的工件表面粗糙度达25 μm，加工质量开始恶化，表明该铣削过程不稳定。该实验说明：双NECD配置能显著提高工艺参数ap的有效加工范围，在保证精加工质量的前提下(见图18)，可明显提高装配界面的精加工效率。

图15 铣削过程中装配界面振动响应的时域及频域信号Fig.15 Vibration signals of assembly interface in time and frequency domains during milling process

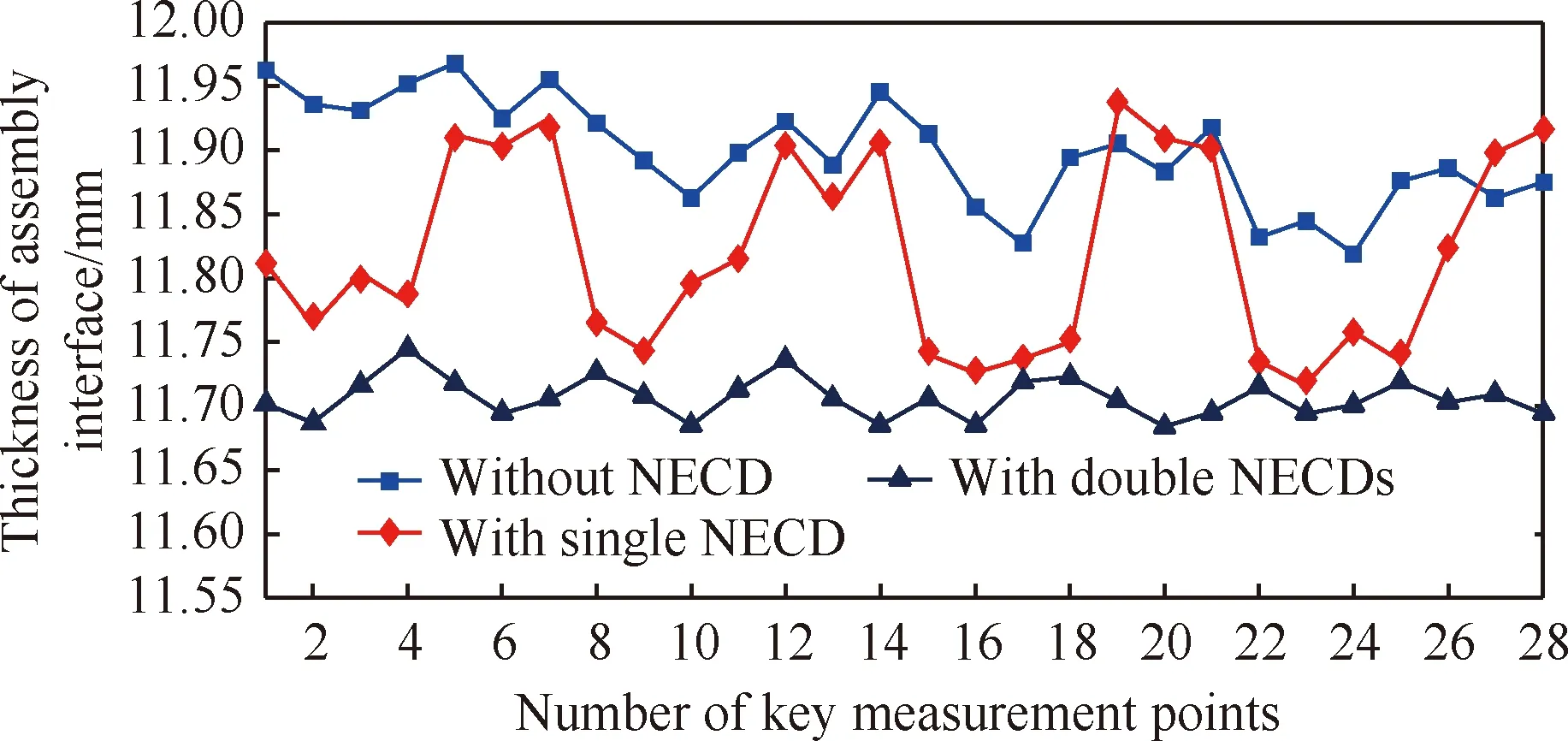
图16 装配界面关键测量点处的工件壁厚值Fig.16 Wall-thickness values of key measurement points of assembly interface

情况2双NECD作用下，其他工艺参数不变，即ae=50 mm，ap=0.3 mm，vf=120 mm/min，改变n大小(n=350，500,550 r/min)对装配界面进行切削实验，得到其振动响应的时域和频域信号及加工后关键测量点的壁厚值分别如图19和图20所示。由图19和图20 可发现，当n=350,500 r/min时装配界面的铣削过程稳定且加工质量较好，但当n增至550 r/min 时，切削过程开始失稳，表面加工质量变差。该实验表明：在满足加工质量的要求下，双NECD配置能显著提高装配界面的动态可加工性，使工艺参数n可提升至500 r/min。

总之，通过以上实验表明：在满足加工质量要求的前提下，双NECD配置能显著提高装配界面精加工过程的稳定性和动态可加工性。据不完全统计，相比于传统精加工方式，双NECD作用下装配界面的精加工时间减少了30%～45%，提高了生产效率。应该说明的是，上述实验只是针对单块装配界面进行的，而大飞机垂尾装配结合面是由八块上述装配界面构成的。在实际精加工过程中只需对每块装配界面各配置两个NECD，便能有效解决装配结合面在精加工过程中出现的铣削振动、回弹变形及根切问题。将进一步开展该项研究与验证工作。

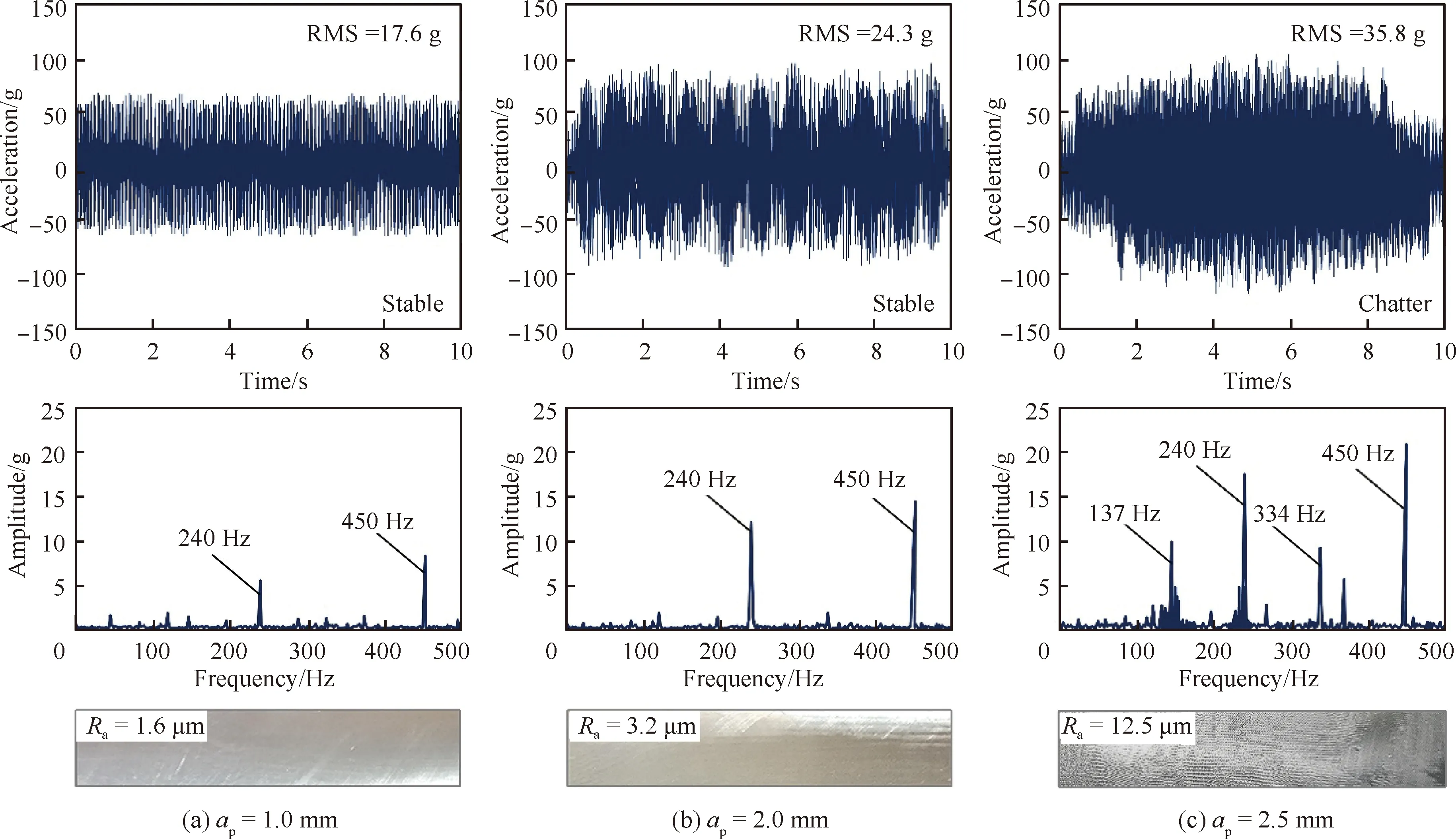
图17 不同轴向切深ap铣削过程中装配界面振动响应的时域及频域信号Fig.17 Vibration signals of assembly interface in time and frequency domains with variable axial cutting depth ap during milling process

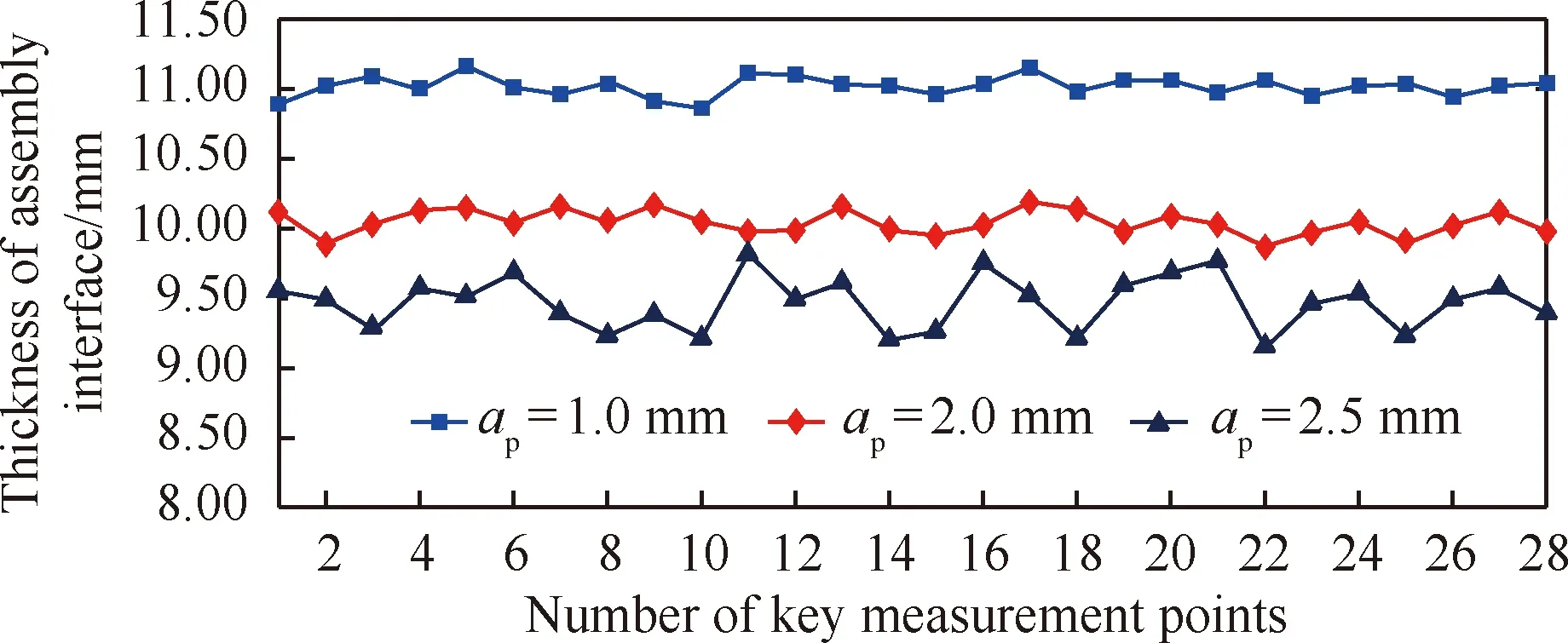
图18 不同轴向切深ap下装配界面关键测量点处的工件壁厚值Fig.18 Wall-thickness of key measurement points of assembly interface with variable axial cutting depth ap

5 结 论

1) 研究并设计了一款用于抑制飞机垂尾装配界面精加工多模态振动的新型电涡流阻尼器(NECD)。该阻尼器由定子和动子组成，可将装配界面产生的振动机械能转化为热能而散失以达到抑振的目的。与传统ECD相比，该阻尼器的导体部分由导体管和导体盘组成，从而在有限的工作空间内增加了电涡流感应区域，使其能产生较强的阻尼效应。动子部分的弹性单元通过执行末端作用于装配界面对其施加动刚度作用，可有效解决装配界面在铣削过程中产生的回弹变形及根切问题。

2) 基于电磁感应原理，建立了NECD阻尼特性的理论模型。该模型揭示了NECD的阻尼特性与装配界面法向振动速度呈线性负相关关系，所产生的阻尼效果与黏性阻尼类似。通过数值计算和有限元仿真方法分别给出了NECD阻尼特性随动子与定子的相对速度、磁极厚度、导体厚度及磁极数的变化规律，为阻尼器关键零组件材料选择和几何参数确定提供了科学依据。

3) 动力学测试结果表明，NECD的应用可使装配界面抑振系统的阻尼比和刚度明显增加，可快速衰减装配界面因冲击激励而产生的自由振动。切削实验结果表明，双NECD配置不仅能提升装配界面精加工过程的稳定性，而且还能明显提高其动态可加工性；双NECD配置是解决装配界面铣削振动、回弹变形和根切问题较优的解决方案。

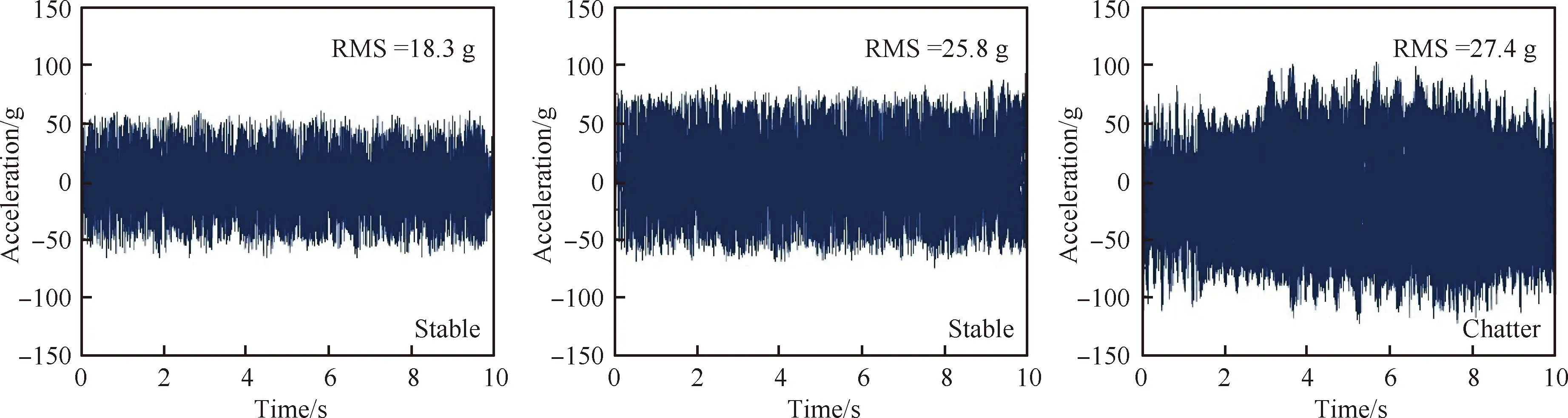
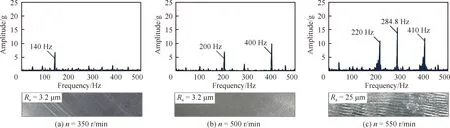
图19 不同主轴转速n铣削过程中装配界面振动响应的时域及频域信号Fig.19 Vibration signals of assembly interface in time and frequency domains with variable spindle speed n during milling process

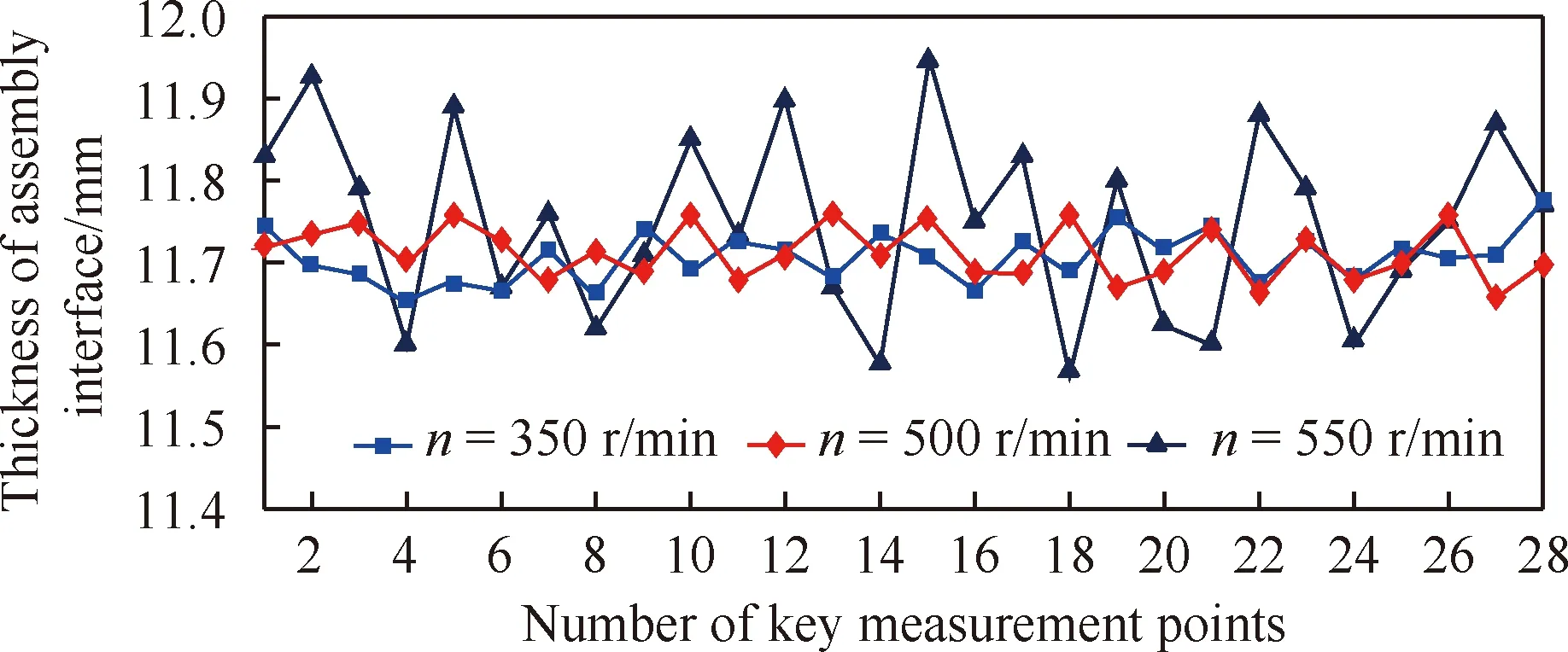
图20 不同主轴转速n下装配界面关键测量点处的工件壁厚值Fig.20 Wall-thickness of key measurement points of assembly interface with different spindle speeds n

由于大飞机垂尾装配界面类似于大尺寸薄壁悬臂梁结构件，其结构刚度较低。不失一般性，本文设计的NECD及相关理论可为航空航天、汽车、船舶等领域类似工件的数控加工提供一定的理论及应用支持，解决加工中出现的振动、回弹变形和让刀等问题。