模块化可重构卫星在轨自重构的分层规划

王博，叶东,*，孙兆伟，唐生勇，陈欣

1.哈尔滨工业大学 卫星技术研究所，哈尔滨 150001 2. 上海宇航系统工程研究所，上海 201109 3. 北京航天长征飞行器研究所，北京 100076

随着微小卫星及其技术的蓬勃发展，结构固定的卫星已经难以满足各国对其提出的多任务执行能力、较强的环境适应性及抗风险等要求，因此人们将目光转向具有在轨变结构[1]能力的模块化可重构卫星。

在传统的设计模式下，卫星的研制周期很长。在轨卫星一旦失效，就需要很长的时间进行重新部署。并且由于现有卫星采用定制研制模式，导致卫星的设计成本和测试成本无法有效降低。

模块化可重构卫星可根据不同任务需求，将原有构型的多个功能卫星模块重组成适应新任务的最佳构型；在局部卫星模块出现故障的情况下，可通过在轨自重构完成备用模块与故障模块之间的替换，具有自修复功能[2]；还可根据发射条件将模块化可重构卫星调整到最佳的发射构型，进入轨道后通过在轨重组恢复到运行及工作形态。图1 为利用空间链式自重构机器人进行装配、合作操纵和自我修复的构想图[3]。

自重构机器人的概念首次由日本学者福田敏夫提出，并且设计了全部由通用连接模块构成的机器人CEBOT[4-5]。但是该机器人模块数目少，执行任务的能力有限。日本产业技术研究所、南加州大学、康奈尔大学等机构分别研发了M-TRAN[6-7]、SuperBot[8]、Molecubes[9]，这些自重构机器人都采用链式结构，相比网格型结构可以实现的构型较少。Telecube[10-11]是美国Xerox Palo Alto研究中心研制的一款以平动为运动方式的网格型结构自重构机器人。文献[12]基于模块平动的特点提出将底部空心的结构下沉填满下层空缺的“梳齿-梳柄”化过程。将这一过程形成的“梳齿-梳柄”结构作为中间构型，并通过逆“梳齿-梳柄”化过程完成自重构。与滑动相比，模块旋转需要额外的间隙。因而，基于滑动模型的算法不能应用于旋转立方体模型。麻省理工学院设计了以转动为运动方式的模块化自重构机器人3D M-Block[13-14]。与文献[12]类似，文献[15]基于转动运动的特点提出了将直线结构作为中间构型，通过直线化和逆直线化实现自重构的规划算法。

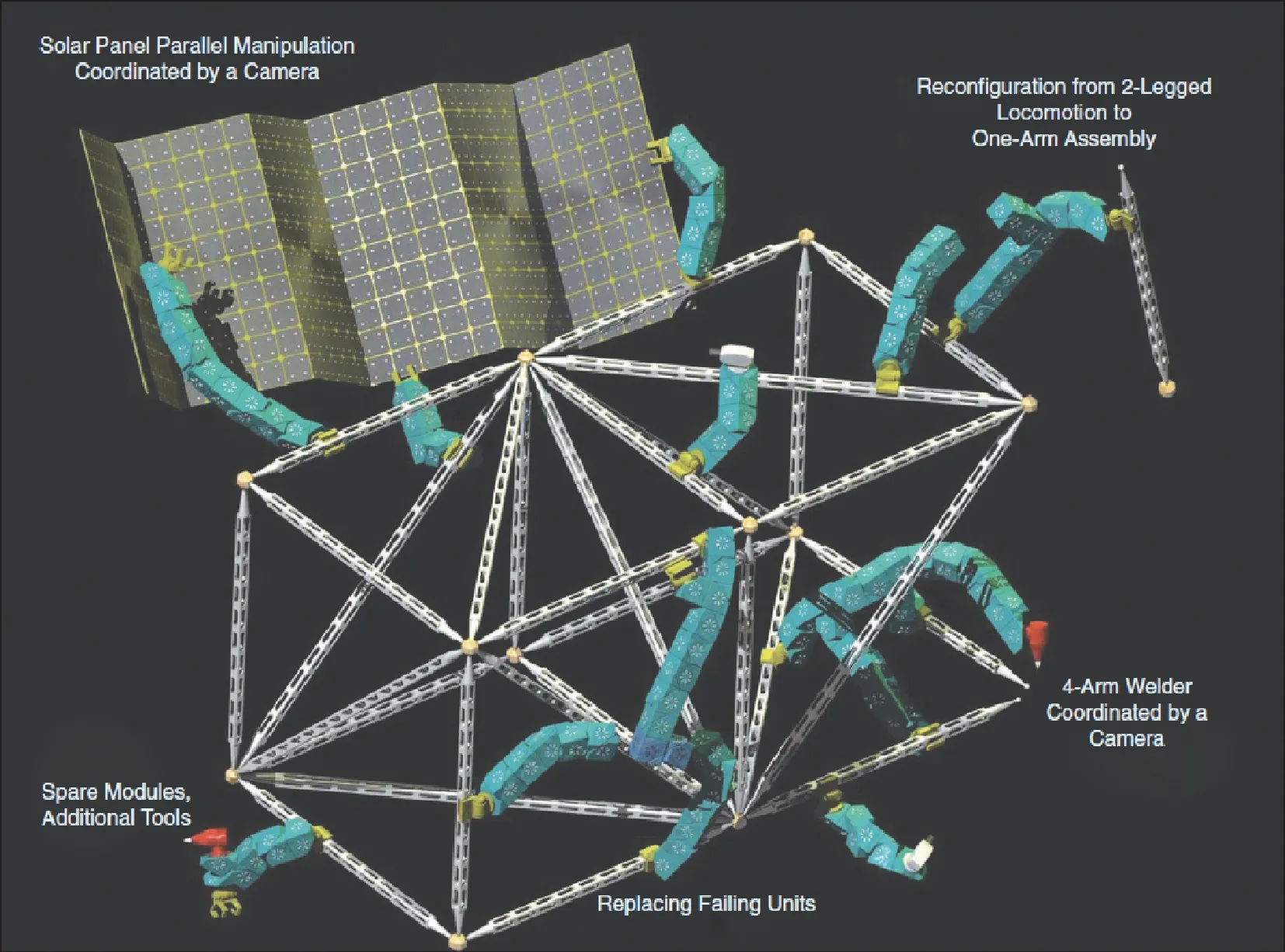
图1 利用空间链式自重构机器人进行装配、 合作操纵和自我修复的构想[3]Fig.1 Idea of using space chain self-reconfigurable robots for assembly, cooperative manipulation and self-repair[3]

但是由于直线构型结构跨度大，整体表现出频率低、模态密集的动力学特征[16]。卫星所处的空间环境复杂、阻尼小，直线构型在模块旋转过程中容易产生大幅振动，并且这种振动不易衰减。因此这一算法不适合应用于航天领域。本文提出一种新的以转动运动网格型自重构机器人为基础的可重构卫星的在轨自重构规划算法。文章内容安排如下：首先，详细陈述了模块化可重构卫星的在轨自重构过程。其次，建立了矩阵形式的自重构模型，并给出了构型、位置矩阵、连接矩阵等概念。再次，给出了模块运动空间的求解算法，并分析了模块三维运动特性。基于分层规划模型设计了重构规划问题的规划算法，并且给出了基于二分图理论和Kuhn-Munkres算法的上层规划以及基于广度优先搜索的下层规划。最后，将提出的规划算法应用于10模块卫星在轨自重构问题，并针对自重构过程中中间构型构型的结构跨度进行了仿真研究。

1 模块化可重构卫星的在轨自重构过程

模块化可重构卫星是一种新概念卫星，由许多功能独立、外形相同的标准模块组成。依靠模块上的传感器感知周围环境信息，在没有外力干预的情况下利用模块间的可连接性和互换性通过模块间的相互运动、连接/分离(卫星在模块运动的过程中保持整体的连通性)改变构型，扩展功能和运动形式。

模块化可重构卫星可以进行组合发射，如图2 所示。设计合理的模块化可重构卫星初始构型，将多个卫星组合成适应发射平台的标准发射构型。入轨后，发射构型分离解体。每一个卫星进行自重构，由初始构型变为执行设计任务的目标构型。接到任务变更指令时，根据任务设计新的目标构型。进行重构规划，得到自重构策略。按照该策略完成自重构，执行新的任务。

图2 模块化可重构卫星的组合发射和在轨自重构Fig.2 Combined launch and on-orbit self-reconfiguration of modular reconfigurable satellites

通过自重构可以解决公用平台针对不同任务和有效载荷的适应性问题。同时可以实现在轨自修复，在轨释放、捕获目标等功能；模块化可重构卫星可以提前发射入轨待命，接到指令后进行变形以完成相应任务，实现对紧急情况的快速响应；当卫星的某一执行机构失效时，模块化可重构卫星可以通过自重构适当调整相应的安装矩阵，保证卫星可以继续正常工作。原理框图如图3所示。

2 模块化可重构卫星的相对位置建模

2.1 模块化可重构卫星的构型

为了描述后续研究内容，提出构型的概念：具有一定连接关系的模块集合、位置集合或模块位置混合集合在三维空间中的结构形式称为构型。模块化可重构卫星的一个构型C由n个模块构成。两个面接触的模块通过施加在接触面上的相互作用力连接在一起，彼此称为对方的相邻模块。模块化可重构卫星所有模块的连接关系可以用图g(ν,ε):顶点集合ν={i:i为C中的模块},边ε={(i,j):模块i,j互为相邻模块}来表示，称为构型C的拓扑连接图，如图4所示。

图3 模块化可重构卫星在轨自重构原理框图Fig.3 Block diagram of modular reconfigurable satellite on-orbit self-reconfiguration

图4 构型的拓扑连接图Fig.4 Topological connection diagram of configuration

基于构型的概念定义卫星自重构：给定模块数均为n的初始构型C0和目标构型Cgoal，在保证构型连通性并且模块之间不发生碰撞的前提下，通过模块的运动使构型C0经历一个构型序列(C0,C1,…,CT)最终变为Cgoal。重构规划问题就是求解构型序列(C0,C1,…,CT)。

2.2 构型的位置矩阵

位置矩阵是构型对应集合中各元素之间相对位置的描述。定义一个三维坐标系，模块i可由它的坐标(xi,yi,zi)表示。xi,yi,zi∈Z，模块的边长作为一个单位长度。按照ν中的顺序将模块的坐标向量排成一列，使第i行对应模块i，这就定义了模块化可重构卫星的位置矩阵V。如果将位置也用坐标表示，就可以得到构型的位置矩阵。

当模块i的坐标(xi,yi,zi)包括在构型C的位置矩阵中时，称i∈C。定义构型位置矩阵的集合运算如下。

定义1(交运算)f∩称为位置矩阵的交：Va和Vb是构型Ca、Cb的位置矩阵，f∩(Va,Vb)=Va∩b。Ca∩b是构型Ca与Cb的公共模块组成的构型，使得∀i∈Ca∩b满足i∈Ca且i∈Cb。若构型Ca与Cb没有公共模块，称他们的交集为空，表示为f∩(Va,Vb)=0。

定义2(并运算)f∪称为位置矩阵的并：Va和Vb是构型Ca、Cb的位置矩阵，f∪(Va,Vb)=Va∪b。Ca∪b是构型Ca与Cb的公共模块组成的构型，使得∀i∈Ca∩b满足i∈Ca或i∈Cb。

2.3 构型的连接矩阵

(1)

利用N可以计算出模块i相邻位置k的坐标：

vk=vi+N(k)

(2)

式中：N(k)表示矩阵N的第k行。

定义连接向量e表示模块i的连接情况，e为一个六维向量，它的第k个元素ek表示标号为k的相邻位置是否有模块与i连接。ek∈{0,1}，满足：

(3)

按照ν中的顺序将模块的连接向量排成一列，使第i行对应模块i，这就定义了模块化可重构卫星的连接矩阵E。已知构型的位置矩阵可以推算出构型的连接矩阵。

3 自重构过程中的运动空间与运动特性

在相对位置的约束下可以对模块的运动进行离散化分析，研究模块一步运动结束后到达的位置，以此建立自重构运动模型。

3.1 立方体模块旋转运动的PCM模型

模块在旋转的过程中，除了初始位置和运动结束后的位置，还需要扫过一片额外的区域。这片区域的存在意味着利用模块平移进行自重构和利用模块旋转进行自重构这两种方式在研究上存在根本性的区别。因而，人们在研究这片区域对运动影响的过程中建立了专门描述利用模块旋转实现变构的自重构机械系统单个模块运动的旋转立方模型(Pivoting Cube Model，PCM)，如图5所示。

在PCM模型中，模块旋转尽可能大的角度。这就意味着在它有一面与其他模块接触前运动不会停止。由于旋转的模块为立方体型，旋转扫过的最大区域取决于模块在旋转面内投影的对角线扫过的面积。PCM模型给出了模块旋转需要满足的5条假设：

1) 旋转模块围绕与另一个模块共享的边缘(转轴边缘)旋转。

2) 正在旋转的模块扫过的区域不能和其他模块区域相交。

3) 旋转扫过的区域在同一平面内，该平面与转轴垂直。

4) 在不旋转期间，模块位于立方晶格上。

5) 连接的模块必须共享一个面。因此正在进行旋转的模块是无连接的。

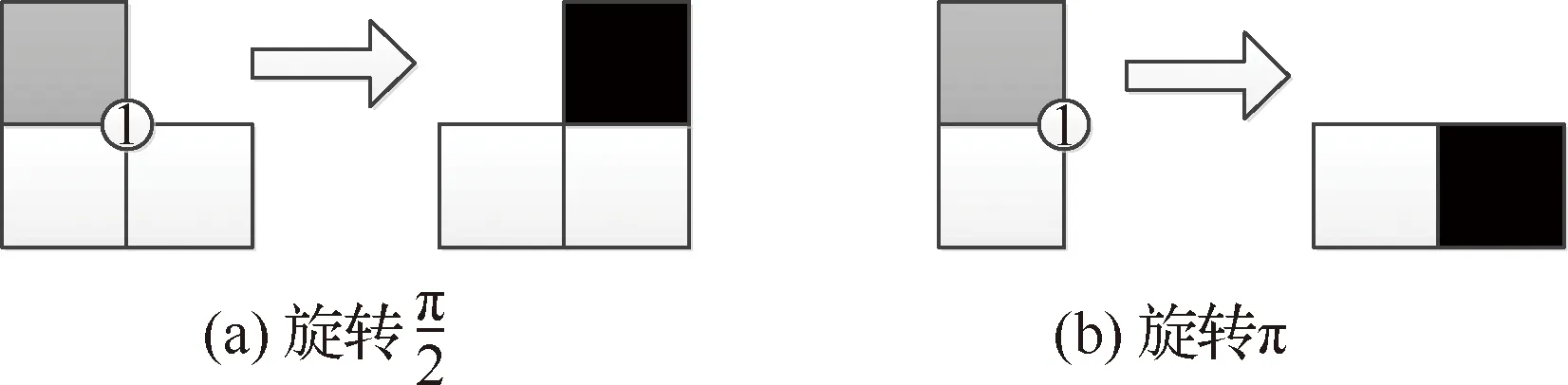
图5 PCM模型下的模块旋转运动Fig.5 Module rotation under PCM model

3.2 模块在当前构型下的运动空间及其求解

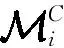
不考虑连接情况，模块共有6个可能的运动方向。为了研究的方便，将模块刚开始运动的速度方向定义成模块旋转运动的方向。

对于立方模块，运动方向总是与模块本体系坐标轴平行。因此运动方向可以用相应坐标轴方向的标号表示，在本文中用d表示。

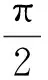
(4)

式中:i为旋转模块；vi为其坐标向量。在旋转过程中，模块运动的路径经过图6中的位置1、2。

(5)

式中:v1、v2分别是位置1、2的坐标向量，表达式为

v1=2vi-vj

(6)

v2=2vi-vj+N(d)

(7)

式中：j为相邻模块；vj为其坐标向量。

同理可得模块旋转π到达的位置可以表示为

vπ=vj+N(d)

(8)

(9)

式中：v3、v4分别为位置3、4的坐标向量，表达式为

图6 旋转过程中扫过的位置Fig.6 Swept position during rotation

v3=vi+2N(d)

(10)

v4=vj+2N(d)

(11)

定理在保证连通性的前提下，模块i绕相邻模块j沿方向d旋转：

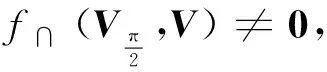
枚举出模块在平面内所有可能的连接情况，利用定理1进行分析可以得到运动空间，如图7所示。

模块i绕其相邻模块j的旋转可以在两个平面内进行，这两个平面均与i、j连接面垂直。i绕j的空间运动可以分解成两个平面运动进行研究，运动空间为各平面内运动空间的交集。在每个平面内运动有顺时针和逆时针两个运动方向。

对每个相邻模块讨论这两个平面内的4个运动方向可以遍历模块i所有可能的运动形式。除此之外，模块的运动不能破坏构型整体的连通性。借用图论中割点的定义[17]，模块可以运动的前提是该模块不是构型的割点。根据以上两条结论可以得到求解模块运动空间的算法1。

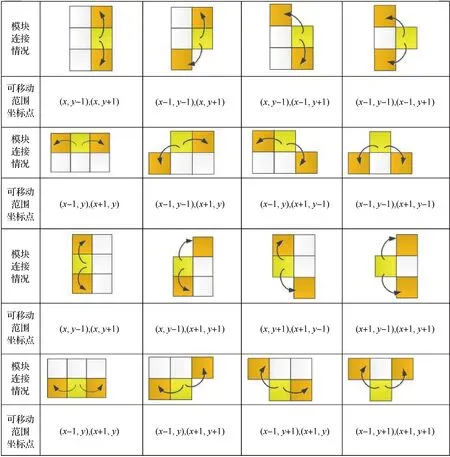
图7 模块在平面内运动的所有可能情况Fig.7 All possible cases of module motion in the plane

算法1 运动空间输入:位置矩阵V,模型i坐标vi输出:运动空间Ci1:if i为构型的割点then2: Ci=03:else4: Ci=0 %运动空间初始化为空集5: Vη^i←相邻位置6: Vηi←f∩(Vη^i,V)7: for all j∈η do8: for all 可能旋转的方向d do9: 计算Vπ2和Vπ10: if f∩(Vπ2,V)=0 then11: if f∩(Vπ,V)=0 then12: 将vπ2加入Ci13: else if f∩(Vπ2,V)≠0 then14: 将vπ加入Ci15: end if16: end if 17: end for18: end for 19:end if20:return Ci

输入任意构型C的位置矩阵V和构型中任意模块i的坐标vi，算法1可以求解i在C中的运动空间。首先判断i是否是C的割点。如果是，i的运动空间为空集。模块根据自身连接向量搜索到相邻模块。遍历绕该相邻模块旋转的4个 移动方向，计算旋转经过的位置。根据定理3确定在各方向旋转的角度，将旋转到达的位置添加到i的运动空间中。对每一个相邻模块都按上述方法操作就能得到模块的运动空间。

3.3 立方体模块的旋转运动特性分析

当模块i有5个相邻模块时，i不能运动。当i有4个相邻模块时，如果这4个模块在同一平面那么i同样无法运动；当这4个相邻模块不在同一平面时，为保证构型连通性，模块可以移动的必要条件是这4个相邻模块自身至少有2个相邻模块。如图8中所示，由于椭圆形中的3个模块除了运动模块没有其他相邻模块，导致这种翻出运动无法进行。

模块i有3个相邻模块时，i的运动可分为两类情况：① 3个相邻模块中存在2个模块在同一轴线方向；② 3个相邻模块中任意2个模块不在同一轴线方向，如图9所示。第1种情况i只能绕与其他2个模块不在一条直线上的相邻模块运动，需要克服较大的阻力，称为“翻出”运动。

模块i有2个相邻模块时，围绕i可以构成直线型结构和“L”型结构，如图10所示。在直线型结构中i不能运动。模块i有1个相邻模块时，i在4个方向均能旋转，旋转角度取决于相邻模块的连接情况。

通过算法1可以列出模块所有可能的运动情况，称为模块的运动空间构型库。限于篇幅，以下仅列举部分，如图11所示。

图8 4相邻模块运动的连通性Fig.8 Connectivity of four adjacent module motion

图9 3相邻模块的两类情况Fig.9 Two types of three adjacent modules

图10 “L”型结构和直线型结构Fig.10 “L” structure and straight structure

图11 模块部分连接情况的运动空间Fig.11 Motion space of several situations of module connection

4 基于分层规划的重构算法

自重构问题可以分解为挑选模块和移动模块两个子任务的组合，因而适合采用分层规划策略解决。根据Kuhn-Munkres算法明确在轨自重构结束后模块的最终位置，利用广度优先搜索求解模块的最短移动路径，就可以完成重构规划。

4.1 解决自重构问题的分层模型

在自重构过程中，每一步移动都会对之后的重构过程产生影响，这种影响往往是难以预测的。有些影响不会在下一步直接体现出来，而是在若干步后才开始体现。自重构问题的这一特点决定了重构规划是复杂且不确定的。

涉及大量模块在三维空间内运动，直接寻找由初始构型到目标构型的运动路径十分困难，本文提出将初始构型到目标构型的运动拆分为初始构型到中间构型、中间构型到中间构型、中间构型到目标构型的运动。分解的目的在于将一条复杂构型到复杂构型的完整运动路径拆分成多段简单构型到简单构型的运动路径，降低运动规划的难度，增加了运动规划的可操作性。针对上述路径拆分的思想，本文提出分层运动规划方法:上层运动规划解决经历哪些中间构型的问题，属于构型间的规划;下层运动规划解决简单构型到简单构型之间，单个模块由初始位置到目标位置的运动路径问题，属于单个模块的最优路径问题。

虽然传统的动态规划算法同样可以降低前面构型变换步骤对后续变换的影响，但动态规划的优势在于解决具有重叠子问题和最优子结构性质的问题。在本文提出的问题模型下，寻找最优子结构较为困难，因而这一方法并不适用。

算法2 分层规划输入:位置矩阵Va,Vb1:\Kuhn-Munkres算法2:for all eij∈G=(Ga,Cb;E) do3: 最短路径←最短路径(vi,vj,Vka)4: 按最短路径将ai移动到bi5: Vk+1a←移动后的位置矩阵6:end for7:return (Vka)

可以看出，上层规划是一个指派问题，它将目标位置分配给具体的模块卫星去填充。将分配好任务的一模块按下层规划得到的最短路径移动到它被指派的目标位置的过程称为构型更新。完成一次构型更新可以得到一个中间构型。通过合理中间构型就可以在有限步构型更新内完成自重构。每一次构型更新都会从目标构型中尚未有模块到达位置中挑选一个目标位置，并从当前构型挑选一个模块移动到该位置。

分解前的原规划问题不能在多项式时间内验证其最优解，是一个典型的非确定性问题。经过分解得到的指派问题和最短路径问题都是可以在多项式时间内解决的确定性问题，从而降低了问题的不确定性。

4.2 基于二分图模型的最优分配模型

对于两个模块数目均为n的构型Ca和Cb,ai和bi分别为其中的节点。它们之间可以建立一种映射：f:Ca→Cb，将构型中Ca的节点ai与构型Cb中的节点bi对应起来，称之为构型Ca和Cb之间的匹配。简单匹配问题是将构型Ca和Cb中的节点对应，通过简单匹配可以找到上层规划的一种可能的解。但这个解并不一定是最优的。要找到一种使构型改变幅度最小的自重构方法需要在上层规划中进行权重匹配。解决这一权重匹配问题需要建立基于二分图理论的最优分配模型。

给出如下定义：

定义1(曼哈顿矩阵)构型Ca和Cb的曼哈顿矩阵D为一个n×n的矩阵，矩阵中的元素D(i,j)为ai与bi之间的曼哈顿距离。

定义2(匹配矩阵)匹配矩阵M为一个n阶方阵，M(i,j)∈{0,1}。M(i,j)=1表示ai与bi匹配。当匹配完成时，rank(M)=n。

定义3(分配度量)所有匹配在一起的节点ai与bj的权重之和作为构型Ca和Cb的分配度量，用δ表示。δ=trace(M×D)。

定义4(权重矩阵)常用的最优分配算法往往用于求解分配度量的最大值，而上层规划要求曼哈顿距离之和最小，因此要做如下转化：

W(i,j)=dmax-D(i,j)

(12)

在权重匹配中，分配度量最大的一种分配称为最优分配。其分配度量称为最优分配度量，用δC表示。最优分配度量可以作为两个构型之间的一种度量函数，它满足度量函数应具备的3条性质[18]。

将权重矩阵中的元素作为节点ai和bi之间的边eij的权重，可以得到赋权二分图：G=(Ca,Cb;E)。每一种匹配方式都有其对应的赋权二分图。寻找最优分配的任务转化为了寻找赋权二分图G=(Ca,Cb;E)使权重和最小的图论问题。

在二分图理论中，若Ca的每个顶点都与Cb的每个顶点相连，则称为完全二分图。用匹配矩阵表示二分图：

(13)

4.3 上层规划的Kuhn-Munkres算法

利用Kuhn-Munkres(K-M)算法可以得到二分图的最优分配[19-20]。首先介绍算法过程中几个概念的定义。

定义5(顶点标记)给二分图中每个节点都赋予一个实数值，称这个值为节点的顶点标记，用l表示。

若一个匹配是最佳匹配，那么所有匹配在一起的节点ai和bi的顶点标记应该满足:

l(ai)+l(bj)=W(i,j)

(14)

式(14)称为最佳匹配问题的边界条件。

定义7(交错路)[21]设M是G的匹配，G的M交错路是指其边在EM的M中交错出现的路。

算法开始前对节点的顶点标记进行初始化：

(15)

初始化后，按照边界条件至少有一对节点可以形成匹配，即相等子图中至少包含一条边。按照如下方法修改顶点标记l

(16)

更改交错路中顶点的顶点标记：

(17)

通过修改顶点标记可以扩大相等子图的范围。在相等子图中进行匹配的问题可以转化为简单匹配问题，用匈牙利算法解决[22]。直到相等子图中包含构型Ca和Cb中的所有节点，在相等子图中求简单匹配就可以得到二分图的最佳匹配。算法3如下。

算法3 Kuhn-Munkres算法输入:位置矩阵Va,Vb1:D←曼哈顿矩阵2:l(xi)←minb∈B d(ai,b);l(yj)←03:while∃aj∉^Ca do4: 生成相等子图^G5: 用匈牙利算法在^G中寻找最大匹配6: 调整可行顶点标记7:end while8:return(eij)

用图2中的自重构过程验证此上层规划算法，初始构型和目标构型之间的曼哈顿矩阵为

利用Kuhn-Munkres算法求解出上层规划的匹配矩阵为

在上述曼哈顿矩阵中框出匹配模块之间的曼哈顿距离。可以计算出上层规划的曼哈顿距离和为9，是所有匹配中的最小值。

4.4 基于最短路径的下层规划

利用上层规划已经求解出了每个模块自重构后应该到达的位置，根据模块当前位置和目标位置可以通过下层规划设计出每个模块运动的最短路径。

要解决最短路径问题，必须要先建立相应的带权有向图。在下层规划中，对于一个模块在其运动空间中的模块权重为1，其他模块权重为∞。本文采用广度优先搜索，可以在建图的同时找到最短路径。

一个模块在当前构型下可以到的所有位置可以构成一个搜索树。p表示树中节点的层号，其在路径规划中的意义是模块运动的步数，w表示第p层中的节点序号。在搜索的过程中，标记节点的父节点。从根节点出发，直到搜索到目标位置停止搜索。从目标位置依次回溯父节点可以得到模块从当前位置移动到目标位置的一条路径。由于是逐层进行搜索，搜索到的目标位置必是层号最小的一个。这就意味着得到的路径运动步数最少，是最短路径。

5 算例与仿真

用一个10模块的模块化可重构卫星在轨自重构来验证本文所设计的重构规划策略的有效性，卫星初始构型和目标构型的位置矩阵为

图12和图13分别为初始构型和目标构型的示意图。图14为分层规划算法(算法2)得到的模块运动方式(即自重构问题的解)，图中白色立方块表示运动模块的初始位置，深灰色立方块表示不移动模块，黑色立方体表示运动模块的目标位置，浅灰色立方块表示模块移动的路径。可以看出经过6个模块共计19步运动，卫星由初始构型最终变为目标构型，完成了在轨自重构。

图12 初始构型Fig.12 Initial configuration

图13 目标构型Fig.13 Target configuration

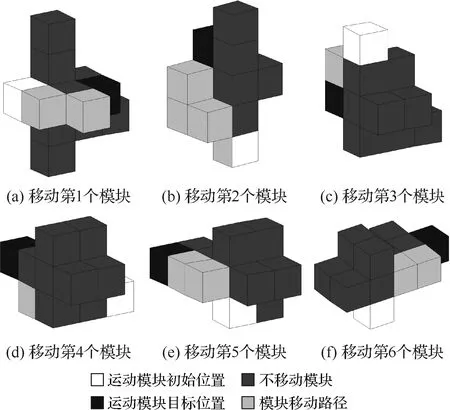
图14 移动第1～6个模块Fig.14 Move the first to sixth module

为了减少文章篇幅和避免重复，只给出第1个 模块移动路径的位置矩阵：

同时给出第1个模块的另外2条移动路径的位置矩阵：

可以看出下层规划中本文采用的广度优先搜索可以得到模块移动的最短路径。

按模块数目从6～50随机生成在轨自重构任务，按本文提出的算法对这些任务进行规划。得到执行重构策略的模块移动总步数，如图15所示。

为方便观察总步数随模块数目增加的变化趋势，以每增长5个模块为一组取步数的平均值，可以看出随模块数目增加该算法求解出的重构方案所需的移动总步数近似线性增长。

图16为按照本文提出的算法对上述在轨自重构任务进行规划的重构未完成度α,α的计算方式为

(18)

同样为方便观察α随模块数目增加的变化趋

图15 自重构所需的总步数Fig.15 Total step to self-reconfogurate

势，以每增长5个模块为一组取步数的平均值。可以看出本文提出的算法更适用于模块数目较多的在轨自重构任务。

利用本文设计的分层规划策略对500个随机在轨自重构问题进行求解，这些自重构问题中模块的数目在6～105之间。图17为按Kuhn-Munkres算法设计的中间构型的结构跨度。在图中，单位长度为模块的边长。

图16 重构算法的未完成度Fig.16 Unreconfigurated rate of algorithm

图17 在轨自重构过程中中间构型的结构跨度Fig.17 Structural span of intermediate configuration during rail self-reconfiguration process

以直线构型作为中间构型[14]，结构跨度等于模块数目。因此可以将直线y=n作为参考曲线。可以看出，按照分层规划策略进行重构可以有效减小中间构型的结构跨度，从而起到避免大幅振动的效果。

6 结 论

本文基于自重构过程的离散运动模型，面向模块化可重构卫星，提出了一种在轨自重构分层规划算法。

1) 创新性地提出用分层规划策略解决重构规划问题。基于二分图模型，利用Kuhn-Munkres算法求解上层规划，实现了中间构型的动态设计。下层规划中利用广度优先搜索可以得到模块移动的最短路径。

2) 仿真实验表明，本文设计的算法可以完成初始构型和目标构型中模块间的最优匹配以及实现重构规划问题的求解。并且验证了相比现有算法可以减小中间构型的结构跨度，更适合应用于航天领域。