一种基于二次分配的测试性指标分配方法

杨鹏，谢皓宇，邱静

国防科技大学 智能科学学院 装备综合保障技术重点实验室，长沙 410073

测试性是装备通用质量特性之一，测试性指标分配是开展装备测试性工程的首要工作，只有将装备顶层的测试性指标逐步分配给其分系统、设备等较低层次，才能将测试性要求逐步落实到各层级的测试性设计中去。

通用质量特性(可靠性、维修性、安全性、测试性、保障性和环境适应性)指标的分配可以采用多种方法，如最简单的方法是等分法，即将上一级的指标平分给下一级，只要下一级产品能够实现其分配的指标，上一级产品即可实现其指标。但为了装备测试性设计更容易实现、设计实现技术风险更小，往往在指标分配时考虑多种因素，如测试性技术较成熟的可多分一些指标，否则少分一些。

国外对测试性分配方法做了大量研究，主流方法是故障率分配法、加权分配法和综合加权分配法[1]，其基本思想是按照各单元的分配权重(如故障率、重要度、测试难易程度等因素)来构造分配函数，然后利用该函数来计算各单元的指标，这些方法统称为函数分配法。针对多个影响因子如何科学量化的问题，国内外学者还研究了基于层次分析法的分配方法[2-4]。

另一类指标分配方法是优化分配法，其基本思想是构建一个融合多影响因素和多约束条件的优化分配模型，然后采用遗传算法等优化算法来获得最优分配结果[5-11]。

上述分配方法适当改进后亦可用于可靠性和维修性指标分配。指标分配问题是目前国内外研究的热点[12-23]。

目前在工程实践中大多采取上述方法之一实施一次性分配，没有反馈迭代。这样的分配方式难以保证各组成单元均能分到合适的测试性指标。如某在研飞机采取一次分配，经过首轮测试性设计和分析发现，不少单元指标分配过高，承研单位付出极大代价也难以满足要求，对此业内普遍认为必须采取多次分配，以得到既满足系统指标要求，又兼顾各单元设计水平的指标分配结果。然而这又带来新的问题：① 应采取多少次分配；② 每次分配采取哪种分配方法；③ 每次分配之间如何实现数据的反馈迭代。

针对上述问题，本文提出一种基于二次分配的测试性指标分配方法，分别针对初次分配和再次分配中存在的问题进行理论分析，提出解决对策和方法，最后进行仿真和实例应用，验证方法的有效性和先进性。

1 二次分配法的技术流程

二次分配法的技术流程如图1所示。

步骤1在开展设计之前，利用有限数据实施初次分配，将总指标分配给组成单元。

步骤2依据初次分配指标对各组成单元实施测试性初步设计，包括：选择测试项目，依据故障传递和测试点布局情况，构建测试性模型，基于模型实施单元测试性指标预计。该步骤的具体方法见文献[1]。

步骤3收集单元测试性指标预计结果、技术成熟度和指标实现成本等数据，判断是否需要再次分配。如需要，则实施再次分配；如不需要，则将初次分配的指标作为单元指标。

两次分配存在的问题和对策研究见2.3节。

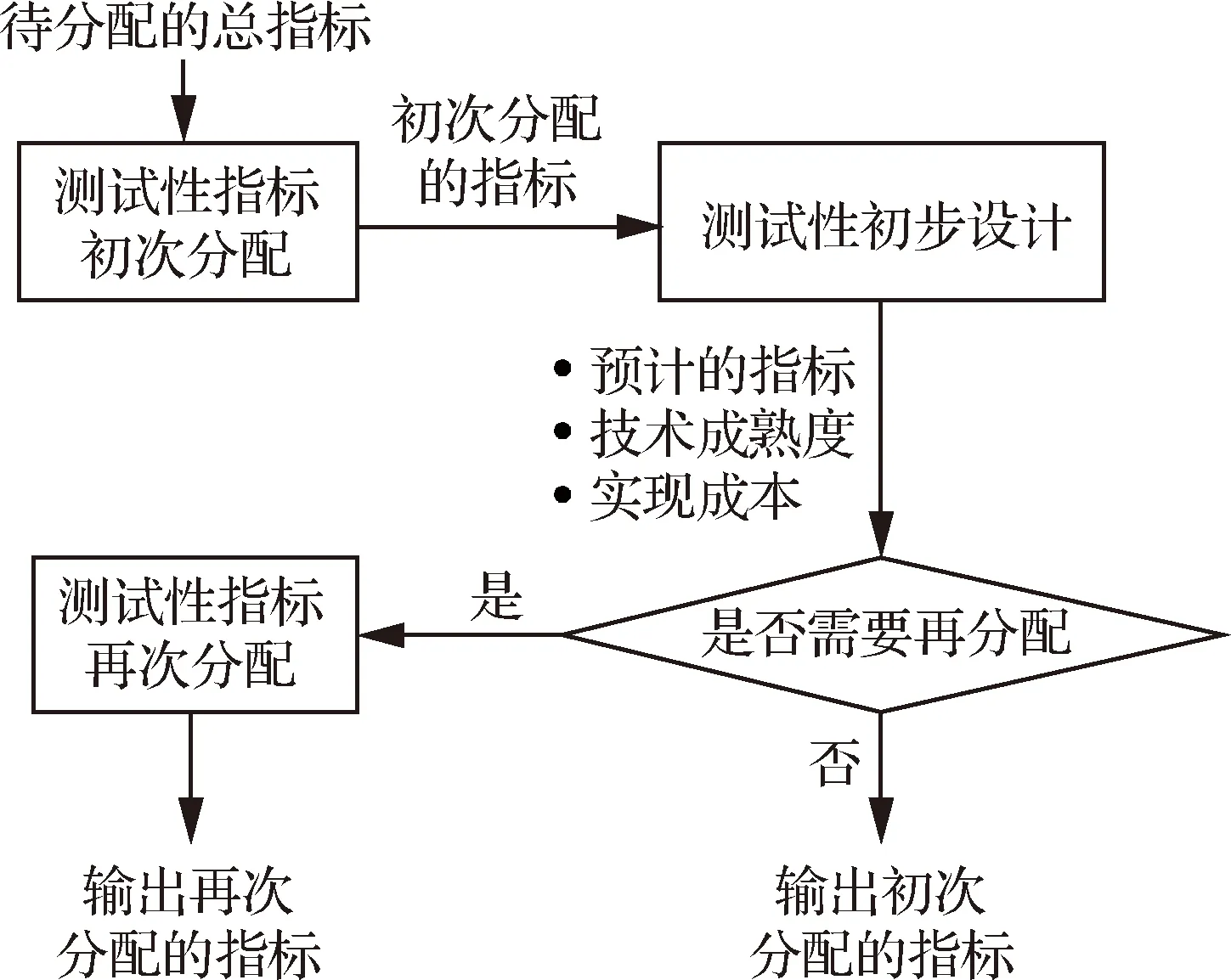
图1 二次分配的技术流程图Fig.1 Flowchart of quadratic allocation

2 初次分配中的问题与方法

2.1 分配模型与问题分析

测试性分配问题在数学上可描述为

γi=f1(λi) 1≤i≤N

(1)

γs=f2(γ1,γ2,…,γN)

(2)

0≤γi≤1

(3)

γsr≤γs≤1

(4)

式中：式(1)为分配函数，γi为第i个单元的分配指标；N为系统组成单元数目；λi为第i个单元的故障率，是分配函数的自变量，若采用加权分配法，则用分配权重因子Wi代替λi；式(2)为验算函数，γs为由各单元的分配指标综合计算得到的总指标，故障检测率的验算式见式(10)；式(3)为边界条件；式(4)为闭合条件，即由分配指标再综合得到的总指标γs不低于要求 (待分配)的总指标γsr，分配后必须检验所分指标是否满足式(4)，称之为指标的闭合性验证。

理论上，初次分配可以采取上述任意一种现有分配方法。但由于初次分配时装备通常处于研发早期，产品尚未开始设计，既无实际的故障率数据，亦无其他可用于指导分配的数据，可能仅有分配的故障率数据或相似产品的故障率数据，因此初次分配只能选择等分法或故障率分配法。而后者能体现各单元指标差异，更好地指导单元设计，如在初次分配时能够获取单元故障率数据，则应尽量采用故障率分配法。

然而经典故障率分配法会出现分配结果大于1，即不满足式(3)的情况，须进行算法改进。

2.2 初次分配函数的推导

经典故障率分配法出现异常结果的本质原因是因为其采用了线性分配函数[1]，没有体现测试性指标提升的一般规律，即：对于测试性水平低的单元，通过改进设计提升其指标相对容易；而对于测试性水平已经较高的单元，进一步提升指标则相对困难。因此，对于分配权重(故障率)较低的单元，不应分配过低的指标，而应分配一个相对值较低而绝对值不低的指标；对于分配权重较高的单元，应分配相对值较高而绝对值不能太高(如逼近于极限值1)的指标。综上，分配函数不应是线性的，而应为一个上凸的抛物线型函数，即单调递增，且增速减缓(一阶导数单调递减)的函数。

令分配函数为

γ=f(λ)

(5)

式中：γ为分配的测试性指标，据分析，f(λ)应满足以下规律:

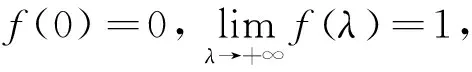
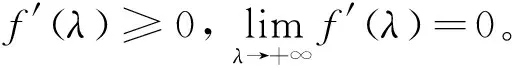
可构造满足规律2的幂函数，即

(6)

式中：A、B、C和θ均为区间(0,+∞)内的常数。不妨取θ=2(可以证明，当取其他数值时，无法同时满足两个规律)，再对式(6)取积分得

(7)

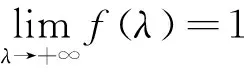
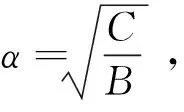
(8)

至此，得到测试性分配函数的一般表达式，这是一个反正切函数，α为一个待定的未知量，它的取值必须使各单元的分配指标满足式(4)。

2.3 初次分配算法设计

依据式(8)，可得故障检测率的分配函数为

(9)

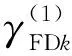
故障检测率的验算式为

(10)

给定要求达到的总的故障检测率为γFDsr，将其与式(10)代入式(4)，有

(11)

将式(11)取等号，代入其他参数，采用数值方法可计算得到α的最小值αmin，本文采用MATLAB的fsovle(·)函数求解得到αmin。

再将αmin代入式(9)，即可得到各单元分配的故障检测率指标。故障隔离率指标的分配函数可依据其定义照此方法类推得到。

同理可构建满足上述规律的指数分配函数：

(12)

式中：ω为待定参数，其满足ω∈(0,1)，参考上述方法可计算得到ω的最大值ωmax，将其代入式(12) 即可得到满足条件的单元分配指标。

2.4 仿真算例

应用文献[1]中的案例进行对比分析。该案例由5个单元构成，待分配的指标为γFDsr=0.95。应用4种方法进行分配，分配结果见表1。

方法1为反正切函数分配法，αmin=0.807 5，其分配结果分布在0.88～0.96之间，满足式(3)，且随着故障率变大，分配指标增幅逐渐减小。

方法2为指数函数分配法，ωmax=0.950 9，其分配结果分布在0.77～0.99之间，比方法1的分布区间大，这是因为指数函数的变化速度比反正切函数大。虽然拉开了各单元指标的差距，但会导致故障率大的单元指标趋近于1，实现难度增大。因此从指标实现角度来看，反正切函数分配法比指数函数分配法更实用一些。

方法3为经典故障率分配法，单元LRU1和LRU2分配的指标仅为0.277 8，LRU4分配的指标到达到1.394 0，这些指标都是不合理的，可见经典故障率分配法的实用性较差。

方法4为综合加权法分配法，其采用多因素(故障率、故障影响、修复时间、诊断难易度、诊断成本)综合加权，加权数据见文献[1]，此方法还需指定分配指标的上限，如本例中指定分配指标上限为0.98。可以看出，由于采取多因素综合加权，分配权重差距缩小，同时限定指标上限，避免了分配指标超过1的情况，但它仍是一种线性分配函数(综合权重的线性函数)，而且分配权重因子和分配上限的确定带有主观性。

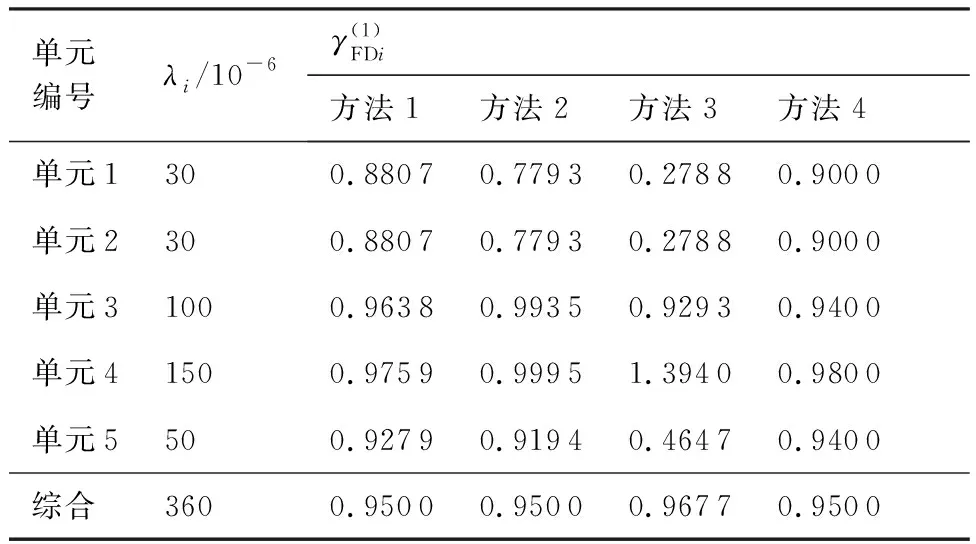
表1 初次分配的仿真案例Table 1 Primary allocation of simulation case

经验算，由4组分配结果综合计算得到的总指标依次为0.950 0、0.950 0、0.967 7、0.950 0，均不低于要求的总指标0.95，通过闭合性验证。

除闭合性验证外，还需进行可实现性验证，即考察所分配的指标是否能够设计实现，这需要结合实际设计反馈来验证，后文将给出可实现性验证方法。

图2给出了以上4组分配方法的结果对比图。可以看出：经典故障率分配法得到的分配结果与故障率呈一条直线，故障率最大的单元很容易超出分配上限；综合加权分配法、反正切函数分配法和指数函数分配法所得到的分配结果均与故障率呈非线性关系；综合加权分配法与反正切函数分配法分配结果最接近。

考虑到反正切分配法所需的数据少于综合加权分配法，而分配结果相近，因此该方法更加简单实用。其他分配方法，如加权分配法、基于层次分析法的分配法以及优化分配法虽未与反正切分配法进行比较，但通过类比分析可知，用这些方法得到的结果应与综合加权分配法差别不大，且所需数据与综合加权分配法相近。因此，可以认为本文提出的反正切分配法优于现有方法。

图2 4种分配方法的结果对比Fig.2 Results comparison among four allocation methods

3 再次分配中的问题与方法

3.1 问题分析

再次分配需要解决的问题是：① 如何判断初次分配是否存在指标偏高/偏低情形，以及确定哪些单元指标偏高/偏低；② 采取哪种方法实施再次分配。

对于问题①，再次分配的时机可选在测试性初步设计之后，此时可依据初步设计结果来判断初次分配指标是否偏高/低，定义如下参数。

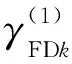
事实上，在满足式(4)的前提下，单元指标修正的一般规律是：不可能全部提高或全部降低，必然是有的降低、有的提高，或者全部不变，这是一个相对的调整过程。据此再定义如下参数。

定义2单元测试性指标实现相对难度系数，记为σk，其计算方法为

(13)

式中：Wk为单元k的测试性技术成熟度，其数值越大则实现单元所分指标的技术难度越低；Ck为实现单元所分指标的预计成本，其数值越大则指标的实现难度越高；M为平均难度系数，其计算方法为

(14)

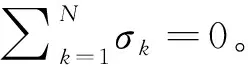
对于问题②，再次分配可采取以下两种方式实施：① 基于此时已有的数据，如故障率、测试难易程度、测试成本等，采用已有方法，如综合加权分配法或优化分配法再分一次指标；② 对初次分配的指标进行针对性的、局部的修正。第①种方式固然可行，但考虑到第②种方式更能体现两次分配之间的迭代关系，且修正的方式对指标偏高/低单元更具有针对性，故本文选择后一种方式。

首先基于指标预计结果判断是否需求进行修正。若对∀k，都有εk≤0，则说明所有单元初步设计结果均满足初次分配的指标，此时无需修正；否则，需要进行修正，修正策略如下：

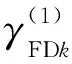
定义3指标修正函数，记为g(x)，其变量x=σk,g(x)满足:

(15)

下面推导g(x)及其边界条件。

3.2 修正函数的推导

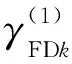
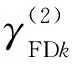
(16)

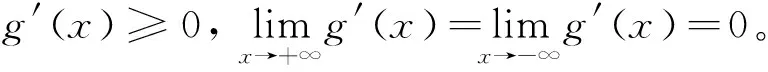
显然g(x)与初次分配函数f(λ)的规律相似，故参考2.2节的推导方法，可得到

g(x)=Darctan(βx)

(17)

将式(16)代入式(17)，可得

(18)

3.3 再次分配算法设计

将式(17)，x=σk代入式(15)，得到

(19)

参数β的计算方法如下：根据式(4)，有

(20)

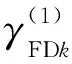
3.4 仿真算例

再次应用文献[1]中的案例，给定单元测试性指标实现相对难度系数(见表2第4列)，应用上述方法计算得到分配结果(见表2第5列)。

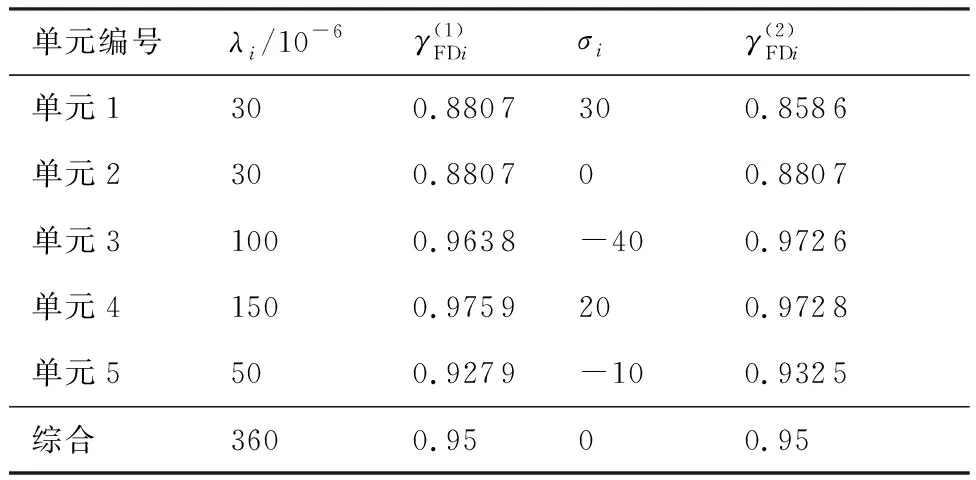
表2 二次分配的仿真案例Table 2 Secondary allocation of simulation case

可以看出：单元1和单元4的相对难度系数为正，所以其指标下调；单元3和单元5的相对难度系数为负，所以其指标上调；单元2的相对难度系数为0，所以指标不变；调整结果符合指标修正的一般规律。此外，从闭合性验算结果来看，两次分配的综合指标均为0.95，通过闭合性验证。

4 实例应用

下面以某案例系统对本方法进行演示验证。该系统由自动飞行控制计算机、自动飞行控制装置、驾驶柱回传作动器、驾驶盘回传作动器、脚蹬回传作动器、主飞控计算机、惯组系统、飞行管理系统和大气数据计算机共9个单元组成。

采取图1所示步骤实施分配。首先进行初次分配，此时案例系统尚处于方案阶段，仅已知待分配的故障检测率指标为0.95，以及经可靠性分配得到的单元故障率数据(见表3第2列)。

鉴于可用数据有限，故采用反正切函数分配法实施初次分配，利用式(11)计算得到αmin=0.255 2，代入式(9)计算得到各单元指标(见表3第3列)。该结果经闭合性验证满足式(4)。

然后，依据初次分配的指标实施测试性初步设计，包括单元失效模式与影响分析(FMEA)，单元测试选择等，据此应用测试性建模分析软件构建系统测试性模型，如图3所示。

应用该软件进行测试性指标预计，得到各单元的故障检测率预计值(见表3第4列)，可以看出各单元均未达到初次分配的指标。而且在设计中发现各单元实现测试的难易程度不同，于是对各单元的测试技术成熟度和测试成本进行评分，再利用式(13)计算得到各单元相对难度系数(见表3第5列)。

应用本文第4节方法实施再次分配，利用式(20) 计算得到βmax=0.000 5，将其代入式(17)计算得到各单元指标(见表3第6列)，该结果经闭合性验证也满足式(4)。

可以看出，自动飞行控制装置和3个作动器实现初次分配指标的难度较大，其相对难度系数均为50，所以再次分配的指标均得到不同程度的下调，4台计算机和惯组系统的相对难度系数为-40，所以再次分配的指标得到上调，这样系统总的指标得以满足，且符合指标修正的一般规律。虽然各单元最终分得的指标均高于单元预计结果，但由于修正过程综合考虑了单元技术成熟度和成本因素，所以相对而言是合理的。

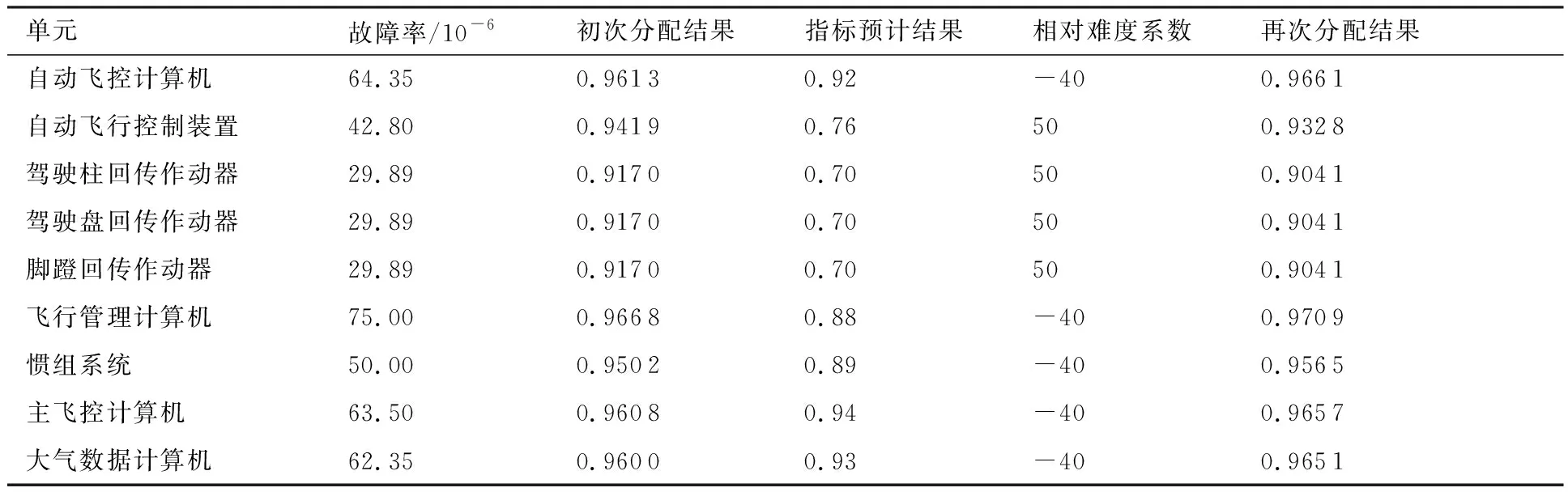
表3 案例系统测试性指标二次分配Table 3 Quadratic allocation of the actual case

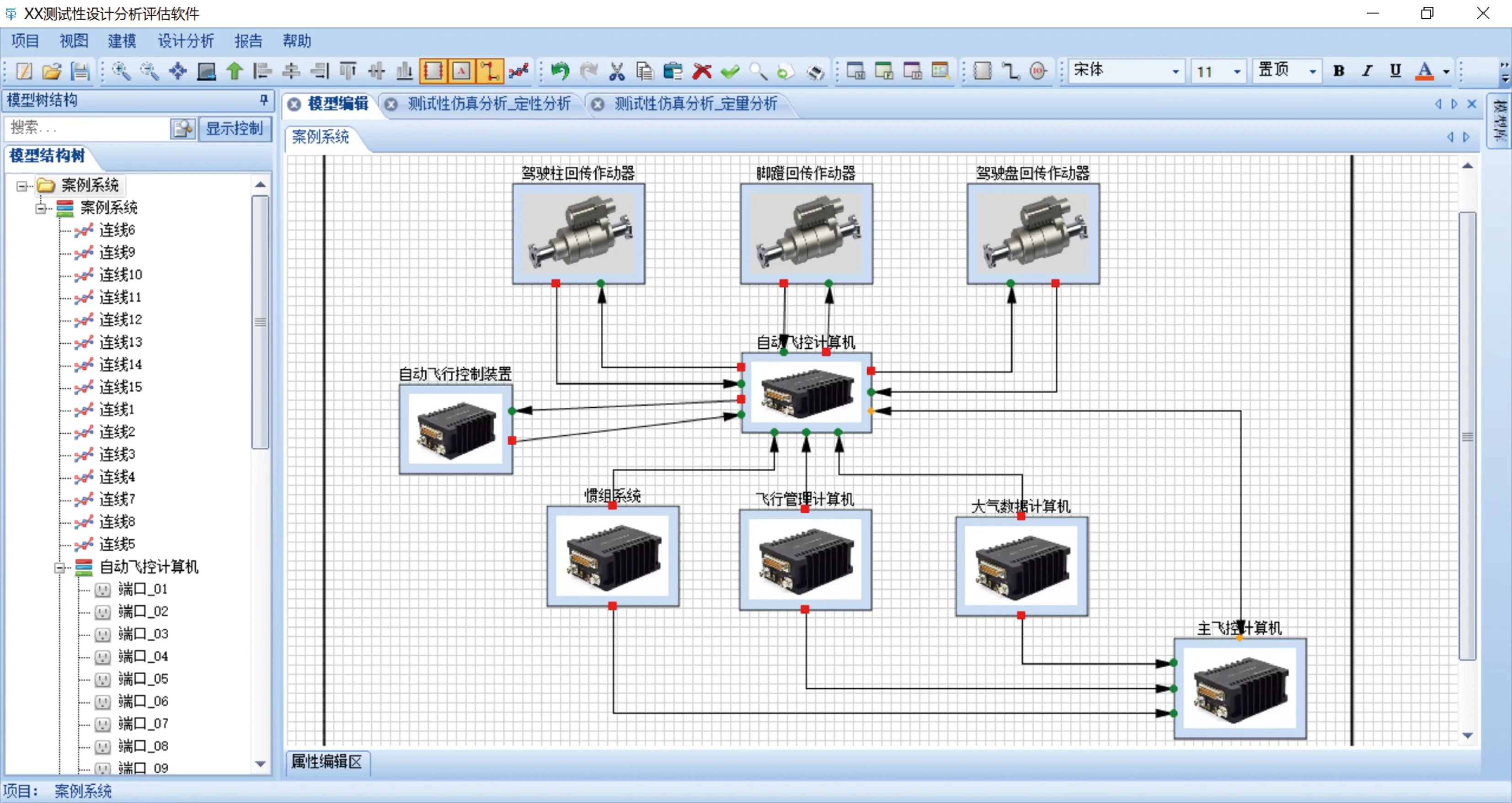
图3 真实案例系统测试性模型Fig.3 System testability model for actual case

最后，对分配的指标进行可实现性检验。定义E(i)描述分配指标的可实现性，其计算式为

(21)

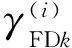
由于本案例系统尚未最终完成测试性设计，故将各单元预计可达到的指标代替最终设计达到的指标，代入式(21)计算得到E(1)=1.072 0,E(2)=1.049 4，二者相比可见再次分配的指标比初次分配的指标更趋紧于预计的单元指标，据此初步判定再次分配的指标实现性更好，即二次分配优于一次分配。

5 结 论

针对目前测试性指标采取一次性分配，缺乏必要的反馈和迭代的问题，提出了一种基于二次分配的测试性指标分配方法，通过指标可实现性验证，该方法优于一次性分配方法。

针对初次分配，提出了一种基于反正切函数的分配法。仿真计算表明，该方法仅利用故障率数据，就得到了与利用多种数据的综合加权分配法几乎相同的分配结果，显著优于仅使用故障率数的经典故障率分配法，证明该方法较为合理，且简单实用。

针对再次分配，提出了一种基于单元相对难度系数的修正函数，对指标偏高/偏低的单元实施局部修正。实例计算表明，经过修正后的指标不仅满足闭合性条件，而且指标可实现性显著优于初次分配的指标。