计入粗糙度的液压缸仿生微织构耦合效应研究*

陈小兰,2 曾良才 湛从昌

(1.武汉科技大学冶金装备及其控制教育部重点实验室 湖北武汉 430081;2.黄冈师范学院机电与汽车工程学院 湖北黄冈 438000)

仿生微织构技术是模仿生物体表面形态特征，通过人为地在物体表面加工一系列具有一定分布规律和尺寸的微小几何形貌，从而改变物体接触表面性能(减摩、抗磨、增摩、减振、降噪、抗黏附等)的一种技术方法和手段[1]，其中以织构减摩性能研究最为广泛。研究表明[2]：仿生微织构技术可以有效改善物体接触表面的摩擦，提高产品的性能，延长使用寿命，已广泛应用于机械密封与润滑、汽车活塞与气缸以及各类轴承等领域，但是将其应用于液压领域的研究却刚刚兴起。将仿生微织构技术应用于液压系统和元件，改善液压系统和元件的摩擦磨损，提高液压系统的工作效率，是实现液压系统节能和长寿命的关键。

MAO等[3]基于质量守恒边界条件，在液压缸缸筒内表面构造圆形微凹坑，通过研究空化气泡的产生、发展和破灭过程中气泡的多少对流体动压力和界面摩擦因数的改变情况，利用仿真分析得到了气泡数的变化改变了液体的密度，进而改变了摩擦性能的结论。张颖等人[4]在活塞表面构造圆形、圆柱形、椭圆形、正方形等多种仿生微织构形貌，分析了不同微织构形貌对液压缸摩擦副动压润滑的影响。CHEN等[5]在液压缸缸筒内表面构造菱形微凹坑，分析菱形微织构形貌结构参数对缸筒表面润滑性能的影响，并对织构形貌进行优化，得出存在最优菱形织构形貌使得缸筒内表面动压润滑性能最佳。上述研究均将仿生微织构建立在光滑的缸筒内表面或活塞外表面，忽略了液压缸摩擦副表面粗糙度因素对仿生微织构表面的动压润滑影响。然而，当液压缸摩擦副间的平均间隙与其自身的表面粗糙度在同一个量级时，粗糙度与仿生微织构的耦合影响不能被忽略[6]。余广等人[7]利用平均雷诺方程对缸筒与活塞的配合处微织构流场进行仿真模拟，探讨了多种织构形貌与表面粗糙度综合作用对活塞表面润滑性能的影响，但尚未进行实验验证。

基于此，本文作者在间隙密封液压缸缸筒的内表面构造仿生微织构形貌，并计入液压缸缸筒内表面与活塞外表面粗糙度的影响，采用等效流量法建立基于平均雷诺方程的液压缸摩擦副动压润滑理论模型，利用五点差分和超松弛迭代法求解雷诺方程，分析不同表面粗糙度与仿生微织构对缸筒内表面润滑性能的耦合影响；同时以液压缸常用材料45钢为试件，采用纳秒激光加工技术，在具有不同表面粗糙度的试件表面构造仿生微织构形貌，利用三维轮廓仪和流变仪进行试件表面的动压润滑性能测试，以进一步探讨织构形貌与表面粗糙度对液压缸摩擦副动压润滑的影响规律。

1 缸筒内表面动压润滑模型的建立

间隙密封液压缸密封间隙的大小主要是考虑对泄漏量的影响。间隙不能太小，否则活塞无法在液压缸缸筒内自由移动；间隙也不能太大，否则液压缸内泄漏严重。因此，密封间隙一般设计为几个微米至几十个微米，液压油在间隙中的流量则属于典型的缝隙流动。因为液压油在液压缸摩擦副缝隙的流动速度不大，故缸筒和活塞之间的缝隙流动通常可认为是层流运动，并将液压油看成牛顿体[7]。同时，为简化模型，通常假设活塞和缸筒之间同心。

1.1 几何模型的建立

鲨鱼游动速度飞快是源于其鱼体表皮肤上布满类似菱形的盾鳞，使其能够减少游动时的摩擦阻力[8]。盾鳞上的脊状凸起称为肋条，肋条之间构成具有圆弧底的沟槽，这些沟槽组成的类菱形形貌的肋条结构具有良好的减阻作用。因此，在液压缸缸筒内表面构造最优仿鲨鱼体表菱形微织构形貌[5]，如图1所示。

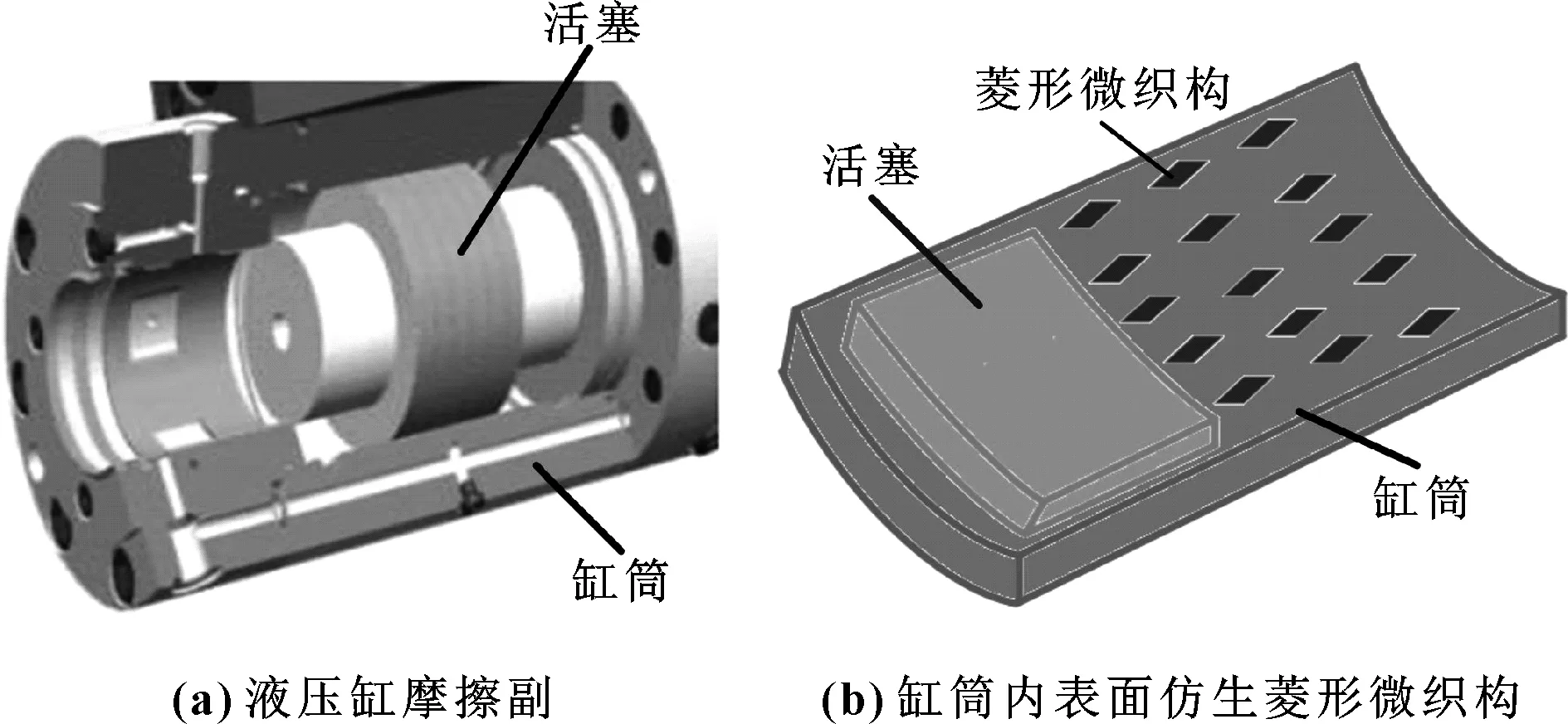
图1 液压缸缸筒内表面仿生菱形微织构示意图

由于摩擦副间隙油膜厚度远远小于摩擦副零件有关尺寸，因此可以忽略二者之间油膜曲率半径的影响。于是可将液压缸缸筒内表面展开成平面进行分析，并建立以活塞运动方向为x轴、以活塞半径方向为y轴的直角坐标系。为了简化计算和节省仿真计算的时间，取一个单元菱形微织构为研究对象，如图2所示。菱形微织构各结构参数如下：织构单元控制边长Lx×Ly为1.0 mm×1.0 mm，织构单元横纵半对角线长a×b为0.5 mm×0.4 mm，织构深度hp为0.006 mm。于是单元织构的菱形织构面积占有率可表示为sp=2ab。

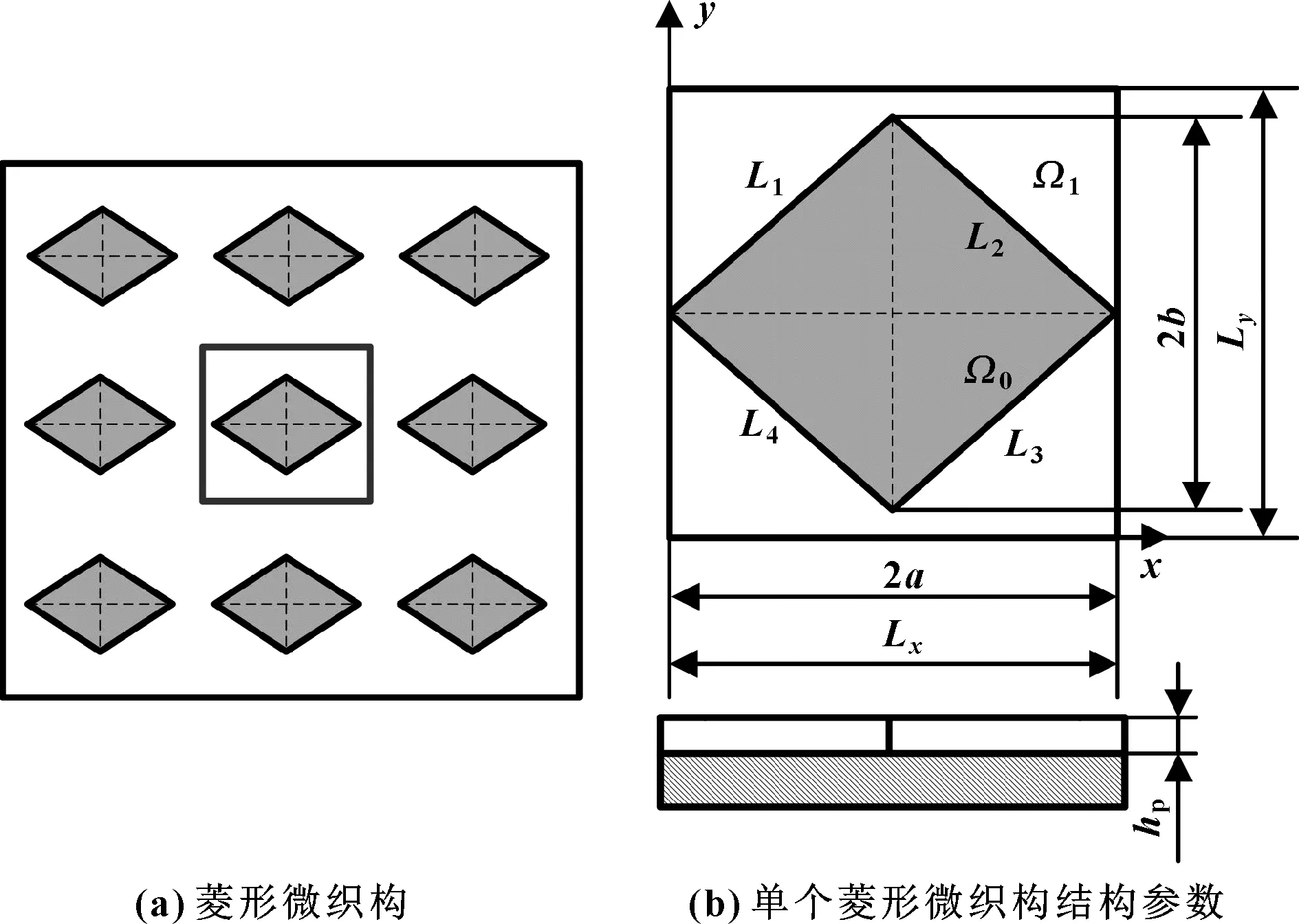
图2 菱形微织构结构参数

1.2 粗糙度接触模型的建立

当考虑液压缸摩擦副表面存在随机分布的粗糙度时，设液压缸缸筒内表面的粗糙度值为σ1，活塞外表面的粗糙度值为σ2。以摩擦副间隙为流场，流场内充满了牛顿体的液压油，若活塞的运动速度为U，摩擦副的最小间隙为h0，考虑摩擦副可能存在表面间直接接触的情况，建立如图3所示的粗糙度接触模型。

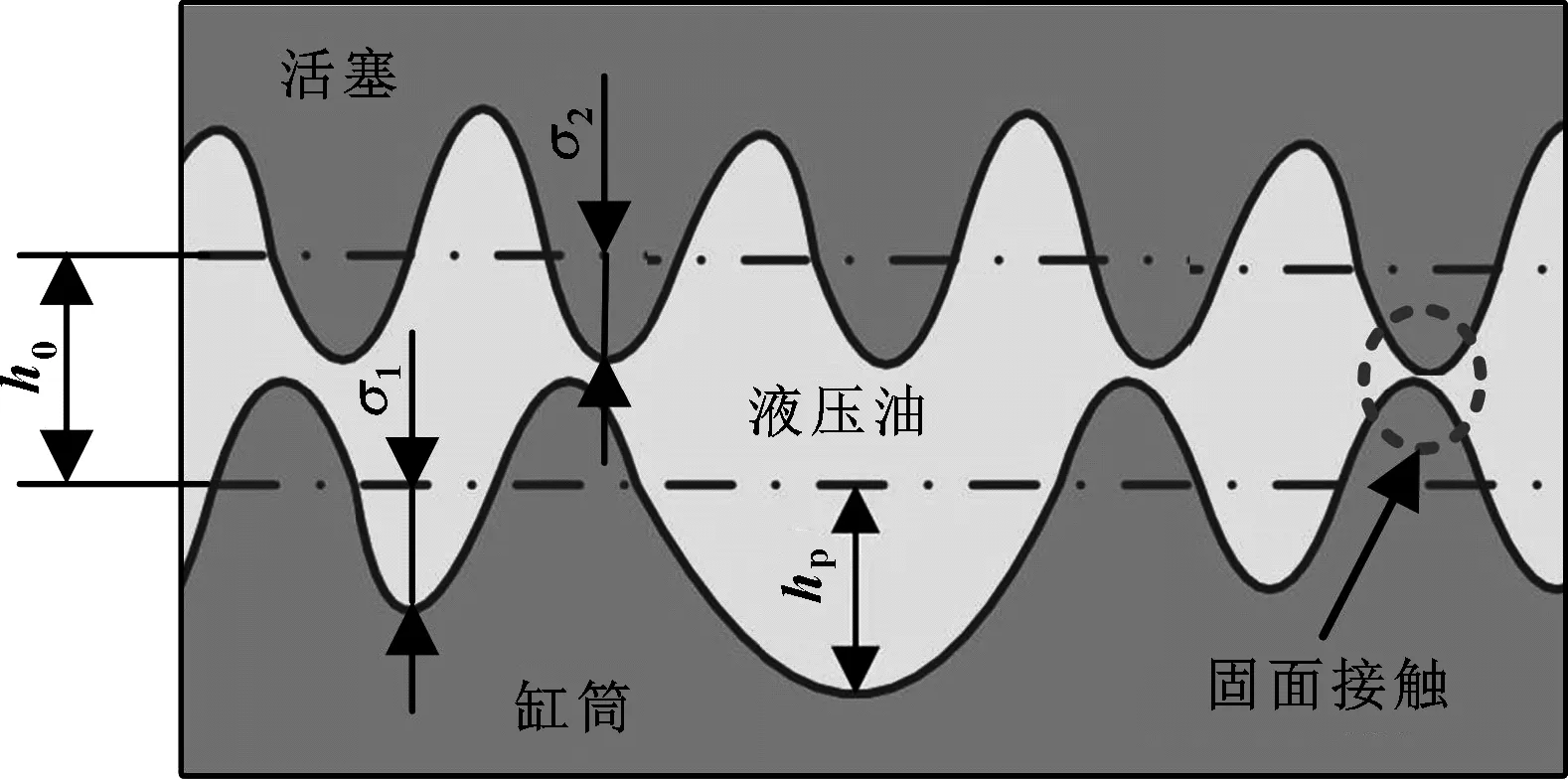
图3 粗糙度接触模型示意图

于是，间隙流场中摩擦副间的间隙就是流场中油膜的厚度。不考虑粗糙度时，由图3可知油膜的厚度可表示为

(1)

式中：Ω1表示非菱形微织构区域；Ω0表示菱形微织构区域，由4条直线组成，即

(2)

考虑粗糙度时，由图3可知实际的油膜厚度变为

hT=h+σ1+σ2

(3)

1.3 控制方程

根据PATIR和CHENG[9]提出的等效流量原理建立平均流量模型，即将表面粗糙度对接触表面的动压润滑影响等效为流量变化的影响，通过引入流量因子来描述，其等效流量表示为

(4)

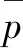
各流量因子的取值可参考文献[10]。同时引入2个参数：膜厚比H，用以描述间隙流场的润滑状态；表面方向参数γ，用以描述表面粗糙度的粗糙峰方向。

(5)

当膜厚比H≥3时表示润滑油膜厚度远大于表面粗糙度值，摩擦副两表面无法接触，流场区域处于完全流体润滑状态；反之表示流场区域处于混合润滑状态，摩擦副两表面可能有接触，此时不能忽略表面粗糙度的耦合效应。表面方向参数γ>1时表现为水平方向条纹，此时侧流很小，粗糙峰对压力流的阻力也很小，这是因为表面粗糙峰的形貌走向与流体的流向相同；当表面方向参数γ=1时，粗糙峰的形貌对油液的走向不敏感；当表面方向参数γ<1时，表现为垂直条纹，此时粗糙峰对油液的流动起阻碍作用，这是因为随着表面方向参数的减小，增大了侧流，使得主流量减小了。

边界条件的选择依据菱形微织构的润滑性质、液压缸摩擦副的运行工况来确定，同时还需兼顾计算的平稳性和精确性。基于此，选择了Reynolds空化边界条件：

(6)

式中：p0为标准大气压。

1.4 摩擦副润滑性能参数的计算

1.4.1 油膜承载力

当间隙流场处于混合润滑状态时，摩擦副表面的油膜承载力W由两部分组成：微织构表面油膜承载力W1和表面粗糙峰油膜承载力W2。

W=W1+W2

(7)

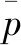
(8)

(9)

1.4.2 摩擦力

当考虑摩擦副表面粗糙度时，缸筒内表面的摩擦力也将由两部分组成：液压油的剪切力和摩擦副间表面粗糙峰接触时的摩擦力，可由下式表示：

(10)

式中：η为液压油的动力黏度；μf为表面粗糙峰间的摩擦因数，在此假设其值为0.1；φf和φfs为剪切力因子，其值亦可参考文献[10]。

1.4.3 摩擦因数

当油膜承载力W和摩擦力Ff均求出之后，即可计算摩擦副表面的摩擦因数：

μ=Ff/W

(11)

2 摩擦性能实验

利用Matlab软件对计入粗糙度的摩擦副表面进行润滑性能数值仿真的同时，文中也开展了模拟液压缸运行工况下的摩擦性能实验，并对摩擦副的表面织构与表面粗糙度耦合效应的仿真结果与实验结果进行对比，以寻找二者间的影响规律。

2.1 试件的制备及表面表征

试件选用液压缸常用材料45钢，其物理和机械性能如表1所示[12]。

表1 45钢性能参数

首先，对试件基体进行机械加工。为了获得不同的表面粗糙度，对个别试件进行了细砂纸打磨和抛光等处理。其次，利用纳秒激光加工设备在试件表面进行仿生微菱形织构加工，微织构横纵间距为1 mm，如图4所示。

图4 试件表面微织构制备过程示意图

最后，利用三维白光干涉轮廓仪对试件表面的菱形微织构及粗糙度进行表征，可以获得试件表面的菱形微织构形貌深度约为6 μm，表面粗糙度值约为0.4 μm，如图5所示。

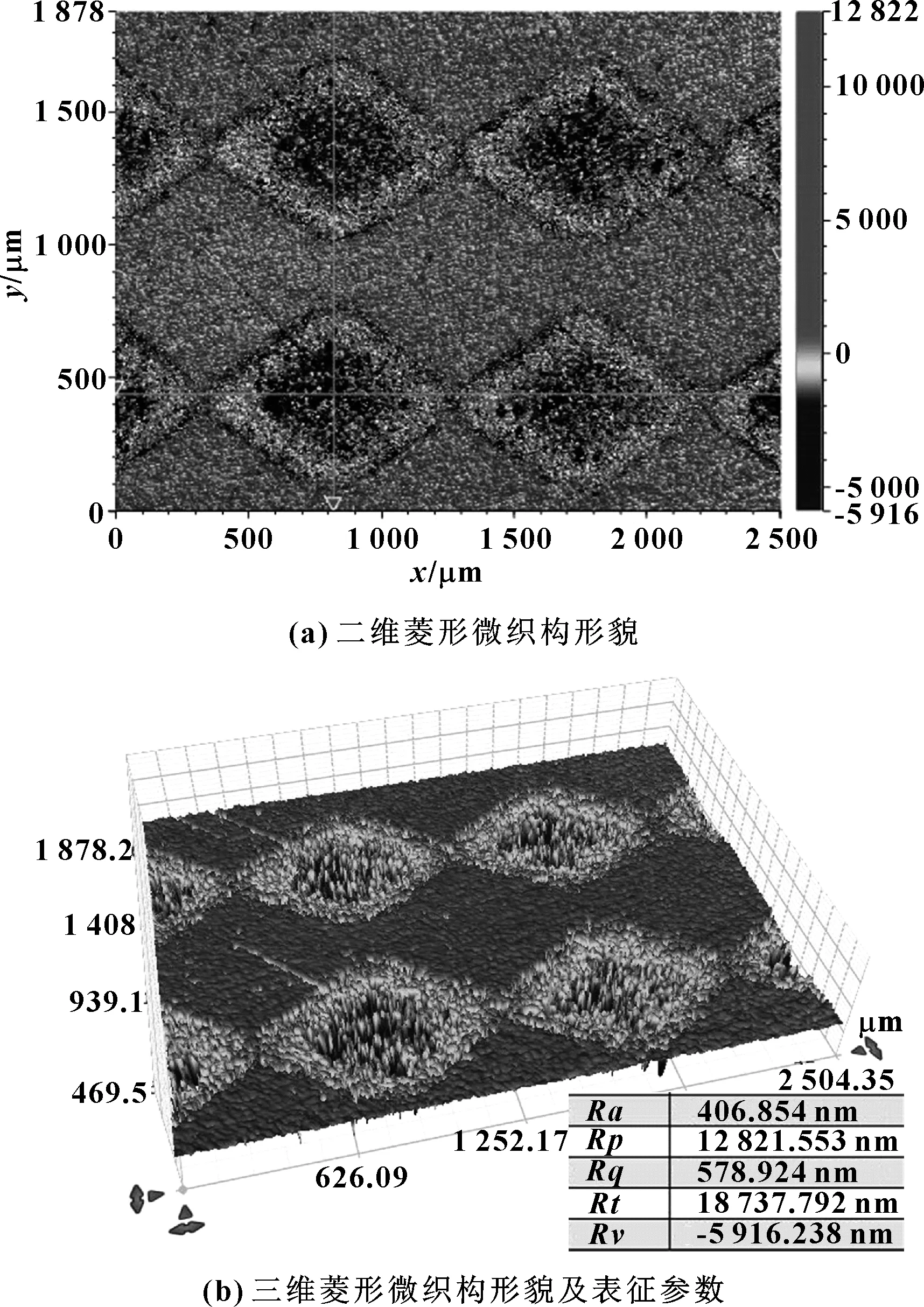
图5 试件表面的微织构形貌及粗糙度表征

2.2 试件的摩擦性能试验

对试件的摩擦性能试验采用AR2000流变仪进行测试，如图6所示。

图6 流变仪摩擦性能测试示意图

为了保证试件试验的精确度，设计了图6中所示的装夹容器方案。将工件置于装夹容器(304不锈钢)中并固定，利用微型水平尺检测控制装夹后试件表面的平行度误差。不锈钢装夹容器内倒入动力黏度值为0.046 78 Pa·s的液压油，并自由放置于流变仪测试工作台，利用容器自身的惯性定位，几何测头选用直径为40 mm的钢平板。

此外，为了验证试件表面的润滑性能是否单纯为粗糙度与织构的耦合效应，另外设计制备了另一组不同菱形织构形貌、表面粗糙度值较低的试件进行对比实验分析。

3 仿真与实验结果分析与讨论

3.1 仿真结果及分析

不同粗糙度值对试件表面压力等值线分布影响如图7所示。可以得出：不同粗糙度的试件表面其油膜压力等值线分布规律基本一致，这是由于所分析的菱形微织构几何结构参数相同，其导致的油膜压力分布区域和分布规律也基本相同；不同粗糙度的菱形微织构表面均产生了动压力，且动压力的最大值均在微织构凹坑偏右侧上下对称分布，这是由于菱形微织构左侧为发散区，发生空化效应，右侧为收敛区，产生微轴承动压效应。但是随着表面粗糙度值的增大，油膜压力最大值也随之增大，这是表面粗糙度耦合作用逐渐加强的缘故。

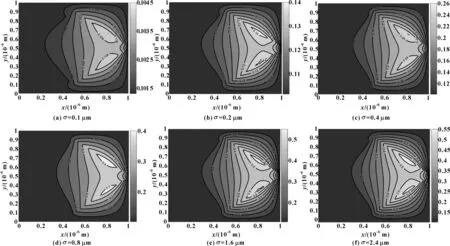
图7 不同粗糙度下摩擦副表面油膜压力等值线分布图

如图8所示，在表面粗糙度与表面方向参数综合作用下，试件表面的摩擦性能有显著的变化。

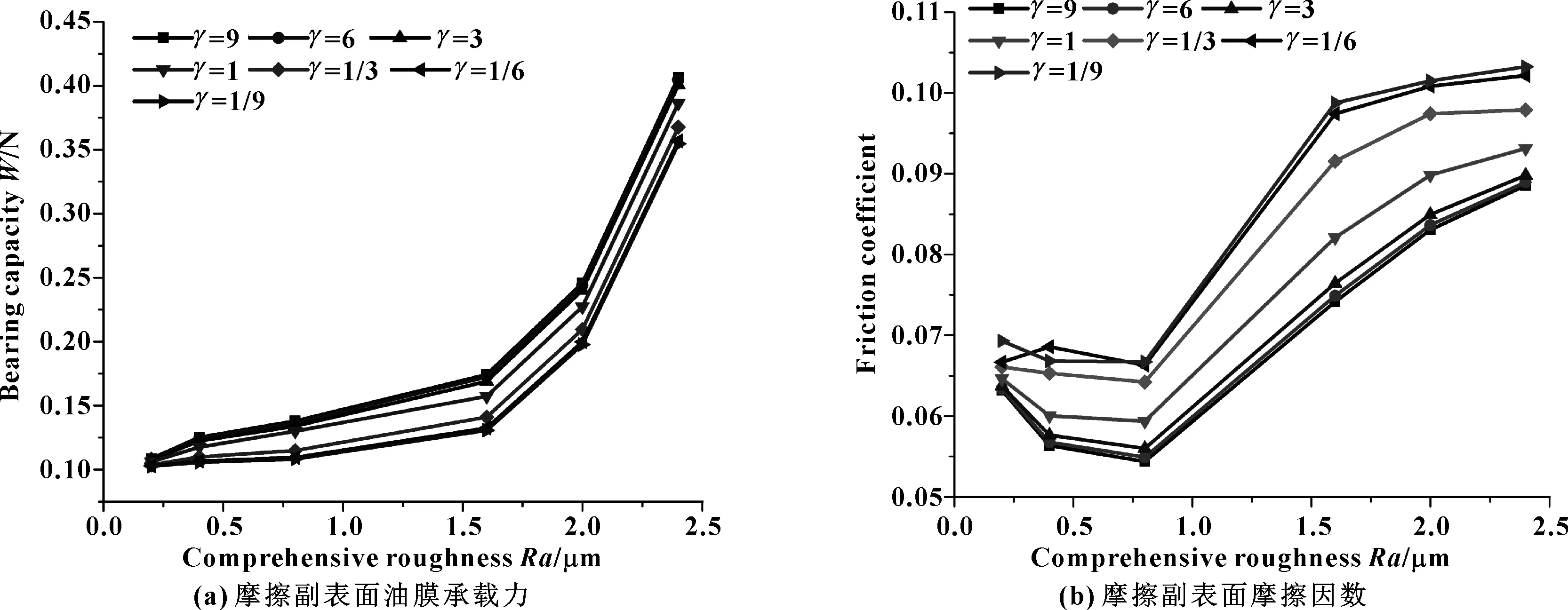
图8 不同方向参数对摩擦副表面承载力及摩擦因数的影响

当表面粗糙峰形貌走向表现为水平条纹(表面方向参数大于1)时，油膜承载力明显大于粗糙峰形貌走向为纵向条纹(表面方向参数小于1)时的油膜承载力，如图8(a)所示。同时，可以发现：随着表面粗糙度值的增大，在粗糙峰形貌走向各不相同时，摩擦副表面的摩擦因数均呈现先减小后增大的变化趋势，即试件表面存在一个最佳粗糙度值，使得菱形微织构试件表面的摩擦因数最小。这说明表面菱形微织构与表面粗糙度的耦合效应，在表面粗糙度值约为0.8 μm时最强。

3.2 试验结果及分析

对10个试件进行表面摩擦性能测试。测试过程分成2组：

(1)第一组：不同菱形微织构结构参数的5个试件，其表面粗糙度值均约为0.4 μm，如表2所示。

(2)第二组：不同表面粗糙度值的5个试件，如表3所示。

表2 不同试件的菱形微织构结构参数

表3 不同试件的表面粗糙度值

调节环境温度为常温26 ℃，流变仪几何测头钢平板与试件表面间距为2 μm，对不同微织构形貌与粗糙度值的摩擦副表面的承载力及摩擦性能进行测试，结果如图9所示。从图9(a)中不难发现：在一定的表面粗糙度下，存在最优菱形微织构形貌，使得试件表面摩擦性能最好；同时从图9(b)中可看出：当微织构形貌一定时，也存在最优表面粗糙度值，使得试件表面摩擦因数最低。这是表面织构与表面粗糙度耦合作用的结果。

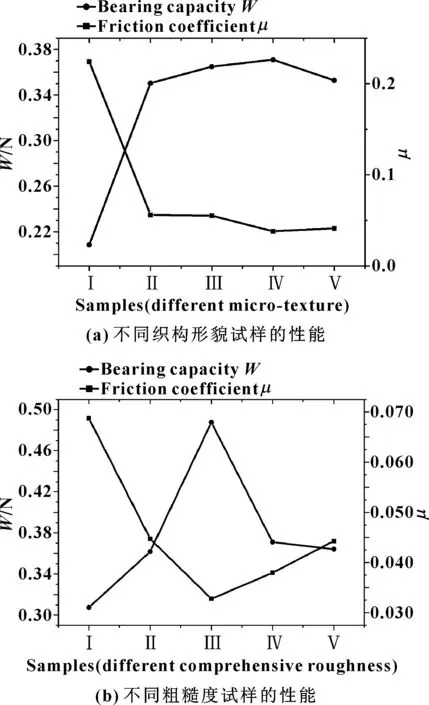
图9 微织构形貌与粗糙度值对摩擦副表面承载力及摩擦性能的影响

当载荷、黏度不变时，速度与摩擦因数的曲线与Stribeck曲线变化趋势接近[6,13]。于是对上述10个试件同时进行不同转速下的摩擦性能测试，结果如图10所示。从图10(a)中可看出：结构尺寸0.5 mm×0.4 mm的菱形微织构的摩擦因数曲线,随着转速的增大最先达到谷底，表明该微织构试件最先从混合润滑状态转变为流体润滑状态。从图10(b)中可看出：表面粗糙度值为0.8 μm的试件也是优先转变润滑状态。这与前面的仿真结果非常吻合。因此，可以得到一组最优摩擦性能组合的摩擦副，即在表面粗糙度为0.8 μm的45钢上耦合横纵半对角线长为0.5 mm×0.4 mm的菱形微织构形貌，可以获得二者耦合作用下最佳表面摩擦性能。

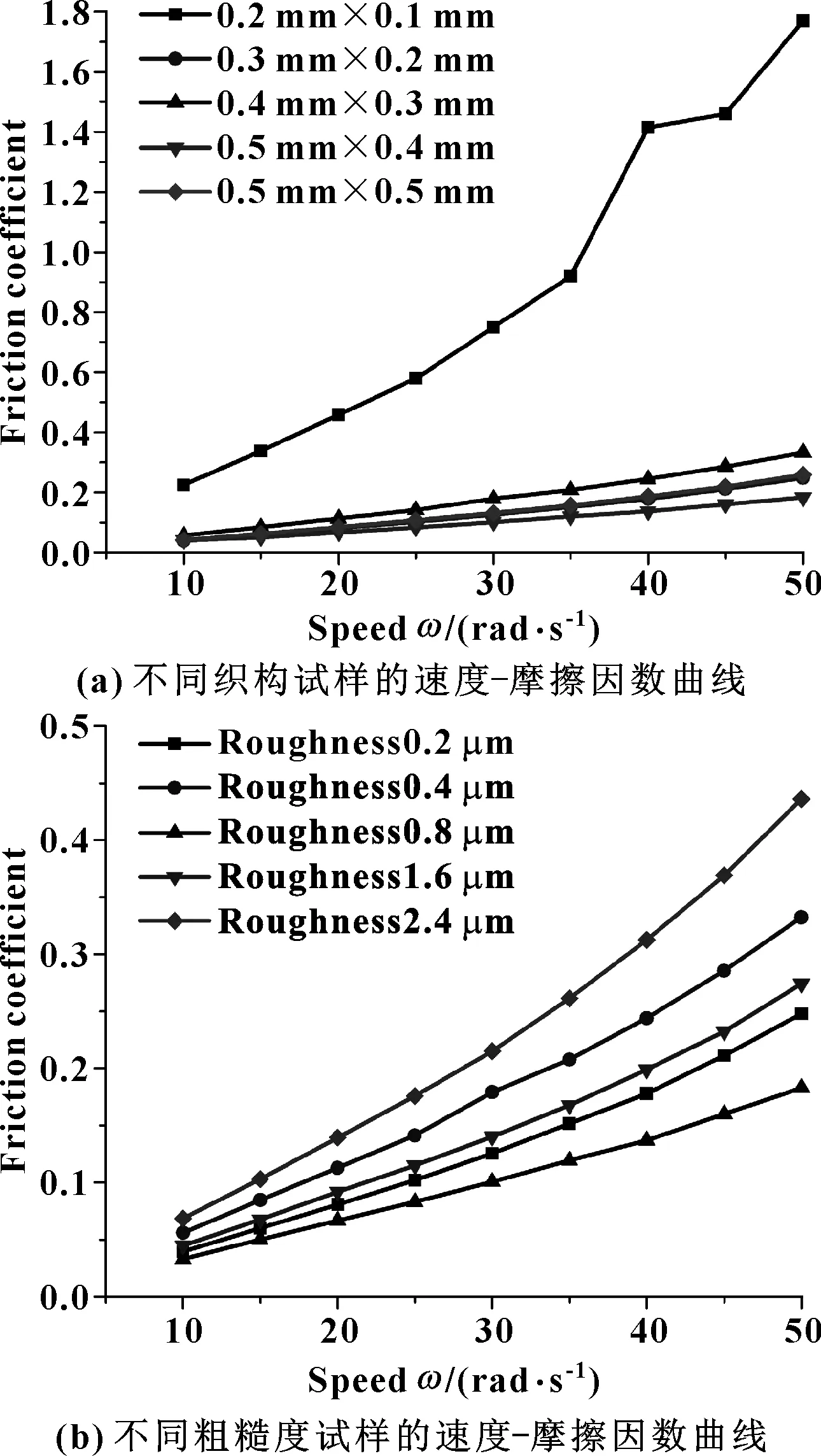
图10 微织构形貌与粗糙度值对摩擦副表面摩擦因数的影响

4 结论

(1)等效流量模型的方法说明，表面粗糙度与表面织构在混合润滑区域对摩擦副表面的摩擦性能耦合作用非常明显，即使试件表面粗糙度纹理走向各不相同，均存在摩擦副表面摩擦润滑性能达到最好。

(2)液压缸摩擦副的表面粗糙度与表面微织构耦合作用明显，合适的表面粗糙度和表面微织构尺寸可使液压缸缸筒内表面从混合润滑状态转变为流体润滑状态，从而增大缸筒内表面的动压润滑效应。

(3)不同菱形织构形貌与不同表面粗糙度的正交实验结果表明二者的耦合效应不能忽略，同时速度与摩擦因数的变化曲线进一步验证二者间存在一个最佳组合，使得摩擦副表面摩擦因数最低。