金融支持、科技进步对供给侧改革影响研究——基于H省样本数据与VAR模型的实证分析

高彦彬，阮非凡

（河南理工大学 财经学院，河南 焦作 454000）

一、引言

在第十三届全国人大二次会议上，《政府工作报告》中提出了2019年我国经济社会发展的总体要求，其中强调了要继续坚持以供给侧结构性改革为主线。供给侧结构性改革作为一项系统性工程，对于推动我国经济高质量发展具有关键性作用。供给侧结构性改革的本质是优化生产要素配置，提升供给体系质量，改善市场供需关系，实现经济增长。根据柯布—道格拉斯生产函数模型Q=A（t）KαLβ（其中Q表示经济发展水平，用来表示供给侧改革成效；A（t）、K、L分别表示科技进步水平、资本供给数量、劳动力供给数量；α、β分别表示资本和劳动力产出的弹性系数），资本供给、科技进步、劳动力供给是影响区域经济发展的三要素，也是影响供给侧结构性改革的三要素，其中科技进步是影响供给侧结构性改革成效的重要因素。而金融是连接科技进步与供给侧结构性改革的桥梁，金融可以通过支持科技进步从而提高供给侧结构性改革的成效。本文以H省为研究对象，从金融支持供给侧三要素之一的科技进步角度着手，从金融支持广度、金融支持强度和金融支持效率三方面，探讨金融通过支持科技进步进而影响供给侧结构性改革的作用机理及其影响程度。

二、文献综述

国外关于“供给侧”的研究起步较早，也经历了曲折过程。亚当·斯密（1776）在《国富论》中开始通过“供给侧”来探究宏观经济发展问题[1]。法国经济学家萨伊（1830）的《政治经济学概论》一书传承了亚当·斯密的思想，主张“供给自动创造自身的需求”，即萨伊定律[2]。此后，阿尔弗雷德·马歇尔（1890）的著作《经济学原理》问世，使经济学中的供给侧和需求侧问题得以同时研究[3]。然而，凯恩斯（1936）在《就业、利息与货币通论》的论著中，主张政府应适当干预经济、刺激社会需求，因此前过于重视需求侧而忽略了供给侧的作用。之后以蒙德尔（1974）、拉弗（1974）、万尼斯基（1975）等为代表的经济学家开始从供给侧的视角来另辟蹊径研究经济[4]。保罗·克雷·罗伯茨（1987）[5]在其著作《供给学派革命》中提出，提高生产率、增加要素有效供给是抑制通货膨胀的有效方法。美国总统里根（1981）提出了“经济复兴计划”，其理论核心就是“供给革命”。20世纪90年代后，美国改变了以往的经济管理模式，采取加税政策，供给侧理念随之渐渐隐退。

国内关于供给侧改革的研究方兴未艾。其中，李月和王珊珊（2018）[6]认为西方结构性改革主要是应对经济衰退以及短期危机，而中国供给侧结构性改革是为了应对中等收入阶段发展困境，实现经济向中高端水平迈进。刘尧飞和沈杰（2016）[7]研究指出，我国经济发展步入了“中等收入陷阱”，供给侧改革势在必行。黄剑（2016）[8]认为供给侧改革的实质是在外部环境及内部要素条件发生改变的情况下，重组生产要素。刘霞辉（2013）[9]主张提高要素供给效率和质量应作为改革的重点，而赵海（2017）[10]则认为供给侧改革还应对产品及产业结构不断改进。勾东宁（2016）[11]提出金融机构的支持是供给侧改革不可或缺的后备力量。许泽玮和施健（2016）[12]认为互联网金融能够同时唤醒供给侧和需求侧“沉睡的资金”，助力供给侧改革取得新突破。张红伟和向玉冰（2017）[13]从居民金融资产配置的视角分析指出，金融能有效促进供给侧要素端和生产端的结构性改革。寇佳琳（2017）[14]的研究显示互联网金融是促进供给侧改革的关键环节，可以解决小微企业因为信息不对称而受到融资约束等问题。李文华（2017）[15]通过对资本市场的分析提出，应促进股权融资，去杠杆、降成本，使补短板工作落到实处。李松龄（2018）[16]从劳动创新理论和资本创新理论两方面对供给侧改革的理论依据进行分析，提出供给侧改革需要科技教育体制、生产资料所有制形式以及收入分配体制等方面的制度变革。

尽管国外学者对供给侧研究较早，其理论基础也较为成熟，但国外学者对供给侧的研究主要集中在传统理论及其改进方面，并且从宏观角度研究的较多而从微观层面量化研究的较少；国内学者关于供给侧改革的研究多是借鉴国外的研究思路与方法，但在指标体系的选取上存在较大偏差。国内有关金融支持供给侧结构性改革的文献有的注重定性理论分析，有的从金融在供给侧改革中的作用、可行性路径等方面进行分析。而供给侧结构性改革是一项系统性工程，影响因素较多，各因素的影响程度也不同，此外我国当前供给侧改革的金融支持现状还存在明显的区域性差异，应对不同地区、不同因素展开有针对性的研究。

本文利用H省的样本数据，从金融支持科技进步为切入点，借助VAR模型实证检验金融支持、科技进步与供给侧改革的动态影响机制，为金融支持科技进步、两者合力助推供给侧结构性改革提供决策参考。

三、研究设计

（一）指标选取

本文将金融发展水平设定为自变量，将供给侧要素指标设定为因变量。根据柯布—道格拉斯生产函数模型，供给侧要素指标应包括科技进步水平、资本供给数量、劳动力供给数量，由于文章只探讨金融通过支持科技进步进而影响供给侧结构性改革的机理，因此资本供给数量、劳动力供给数量不在研究之列，只把科技进步设定为因变量，具体指标及含义如下：

1.科技进步。国内外学者大多从两个角度来衡量关于科技进步：一是科技创新能力，二是科技创新产出。本文基于科技创新产出的视角，以科技创新结果来衡量科技进步。在参考相关文献的基础上，结合H省实际状况以及数据的可获得性，选择专利申请授权数来衡量科技进步，用A表示。

2.金融支持效率。直接融资是在没有金融机构介入的情况下进行的资金融通，直接反映了金融支持的效率，直接融资规模用债券和股票规模之和来度量，以此来反映H省金融对供给侧改革的支持效率，用DF表示。

3.金融支持广度。金融业增加值体现出一个地区的金融发展状况，同时也反映了一个区域的金融业对周边的影响力以及金融深化的程度，以金融业增加值衡量金融支持广度具有一定的代表性，因此本文选用金融业增加值来度量金融对供给侧改革的支持广度，用FGDP表示。

4.金融支持强度。间接融资通过金融中介机构融通资金，间接融资规模体现了一个国家或地区金融机构规模的大小，反映了金融支持的强度，用人民币贷款余额来度量，以此来反映金融对供给侧改革的支持强度，用IDF表示。

（二）数据来源

本文相关数据选自H省1993—2017年度的Wind数据库、《H省统计年鉴》、《中国金融年鉴》以及H省统计局官方信息发布平台，缺失的数据由《H省国民经济和社会发展统计公报》补充。此外，考虑到数据中异方差存在的可能性，而取对数化后的时间序列不会改变原序列的性质，因此本文取各变量的对数形式进行模型的构建及运算。

（三）模型设定

VAR模型是将系统中的各个内生变量当作所有内生变量滞后值的函数来构建模型，以此把单变量的自回归模型应用到多元时间序列变量组成的向量自回归模型。在相互关联的时间序列中，可用VAR模型分析随机扰动项对系统的动态冲击，并对经济变量形成过程中由于各种冲击因素产生的影响进行阐释。本文构建滞后p阶的VAR（p）模型的数学表达式如下：

φt=A1φt-1+…+Apφt-p+B1xt+…+Brxt-r+εt（t=1，2，…，T）

其中：φt为k维的内生变量向量，xt为d维的外生变量向量，p和r表示内生变量和外生变量各自的滞后阶数，T表示样本的数量。k×k维矩阵A1，…，Ap和k×d维矩阵B1…Br是需要估计的系数矩阵。εt表示k维误差向量。

对于不含外生变量的非限制向量自回归模型的数学表达式如下：

φt=A1φt-1+…+Apφt-p+εt

或φt=A（L）φt-1+εt

上式中A（L）是一个以滞后算符L（Lφt=φt-1）表示的具有P个项的多项式矩阵，A（L）=A1（L）+A2（L）+…+Ap（L），εt表示误差项。

本文建立的VAR理论模型为：

φt=A（L）φt-1+εt

φt=（LNA，LNDF，LNFGDP，LNIDF）

εt=（εA，εDF，εFGDP，εIDF）

其中，A（L）是多项式矩阵，εt是误差项向量，LNA是科技进步指标，LNDF是直接融资指标，LNFGDP是金融业增加值指标，LNIDF是间接融资指标。

四、实证分析

（一）单位根检验

为了避免“伪回归”，消除非平稳性，有必要对各时间序列变量进行ADF单位根检验。表1给出了H省金融发展水平以及科技进步时间序列的平稳性检验结果。

表1 各指标单位根检验结果

从表1中可以得出，在原始序列（对数化后）水平上，所有序列的ADF检验值均大于10%显著性水平下的临界值，因此接受存在单位根的假设，即序列均为非平稳序列。对序列（对数化后）一阶差分后的ADF检验值均小于10%显著性水平下的临界值，即所有序列一阶差分后均拒绝了有单位根的假设，表明所有序列的差分变量是平稳的。

（二）最优滞后阶数的确定

依据Eviews软件中所给出的LR（似然比）检验、AIC信息准则和SC信息准则来确定最优滞后阶数。依据判定标准，此处确定VAR模型的滞后期为3（见表2）。

表2 VAR模型滞后期选择

（三）VAR模型构建

建 立DLNA与DLNDF、DLNFGDP、DLNIDF的VAR模型，其估计结果如表3所示（表3中系数下方分别对应标准差和T统计量）。

由表3可得出关于科技进步的如下公式：

由参数估计结果可知，科技进步不仅受其自身滞后值的影响，也受相关变量滞后值的影响，其中滞后1期的直接融资、金融业增加值、间接融资的系数都为正，说明滞后1期的金融业增加值、直接融资和间接融资对科技进步都有正向的促进作用。

（四）检验VAR模型的稳定性

图1是利用Eviews软件作出的AR根图，可以看到所有的数值都落在单位圆内，表明VAR模型是稳定的。

（五）格兰杰因果分析

利用Granger（格兰杰）提出的因果检验方法，检验VAR模型的科技进步与金融业增加值、直接融资、间接融资之间是否存在显著的格兰杰因果关系，以VAR模型最佳滞后期3作为格兰杰因果检验的滞后期，检验结果如表4所示。

表3 VAR模型的估计结果

图1 VAR模型的AR根图

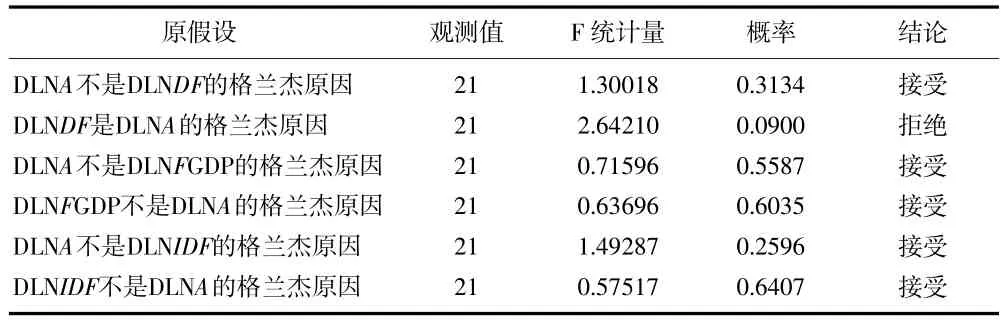
表4 格兰杰因果检验结果

从表4中可以看出：DLNA与DLNDF之间存在单向的格兰杰因果关系，其中DLNDF是DLNA的格兰杰原因，但DLNA不是DLNDF的格兰杰原因；DLNFGDP与DLNA之间以及DLNIDF与DLNA之间不存在因果关系。说明H省的直接融资的发展能够有效促进科技进步，而间接融资的发展和金融业增加值的提升并未能构成科技进步的必要条件。

（六）脉冲响应分析

在向量自回归VAR模型的基础上，分别给DLNA、DLNDF、DLNFGDP、DLNIDF一个标准差冲击得到的脉冲响应函数图解，如图2所示（横轴表示冲击延续的期数，纵轴为冲击影响程度，虚线部分表示正负两倍的标准差偏离带）。

图2 各变量脉冲响应结果

DLNA对自身的脉冲响应如图2左上角所示，科技进步对于来自其自身的一个标准差的冲击立即就有响应，第1期这种响应就达到最大值0.146。随后这种冲击带来的影响逐渐减弱，第4期达到最低点-0.033，随后响应逐渐上升第5期达到0.053后响应逐渐减弱，第7期之后响应维持负值，最终趋于平衡。说明科技进步前期有较强的自我增强作用，后期自我增强作用减弱。

DLNA对DLNDF的脉冲响应见图2右上角，科技进步对于来自直接融资的一个标准差的冲击主要表现为正向响应，在第1期时没有响应，第2期有较小的负向响应，随后响应为正并逐渐增加，第4期响应达到最大值为0.076，随后响应逐渐下降，最终趋于平衡，说明直接融资在长期内对科技进步有正向的拉动效应。

DLNA对DLNFGDP的脉冲响应见图2左下角，科技进步对于来自金融业增加值的一个标准差的冲击会产生正负双向波动，第1～3期与第5～6期呈现出正向响应，剩余各期呈现出负向响应，这说明金融业增加值在短期能促进科技进步，长期内则不利于科技进步。

DLNA对DLNIDF脉冲响应见图2右下角，科技进步对于来自间接融资的一个标准差的冲击也呈现出正负双向的响应，第1期时响应为零，第2期达到正向响应最大值，随后响应逐渐下降，第3期响应降为负值，第4期响应又有所回升达到0.024，随后响应降为负值。可以看出，间接融资对H省科技进步在短期内有正向拉动效应，长期则不利于科技进步。

（七）方差分解分析

方差分解是通过分析每一个结构冲击对内生变量变化（用方差表示）所产生的贡献大小，它反映出了对VAR模型变量产生影响的每个随机扰动的相对重要性情况。本文利用方差分解技术分析科技进步与金融发展三个指标相互之间的贡献率，方差分解结果如表5所示。

表5 科技进步的方差分解结果

由表5可以看出，科技进步对其自身的贡献程度处于不断下降的趋势，从第1期的100%，下降到第10期的58.14%，总体来看科技进步预测方差大多是由自身扰动所引起的。在短期内间接融资对科技进步的贡献作用较大，长期内直接融资对科技进步的贡献作用最大，金融业增加值对科技进步的贡献程度最小，其中直接融资对科技进步的贡献程度基本维持在22%左右，间接融资对科技进步的贡献度基本维持在11%左右，金融业增加值对科技进步的贡献度基本维持在8%左右。

五、研究结论与建议

本文系统分析了金融支持科技进步助推供给侧结构性改革的内在机理，构建了科技进步与金融支持效率（直接融资）、金融支持广度（金融业增加值）、金融支持强度（间接融资）三个指标的VAR模型，在模型稳定的基础上利用H省1993—2017年的数据对变量进行了格兰杰因果关系检验、脉冲响应分析和方差分解。

格兰杰因果关系检验结果是直接融资与科技进步之间存在单向的格兰杰因果关系，直接融资是科技进步的格兰杰原因，但科技进步不是直接融资的格兰杰原因；间接融资和金融业增加值都与科技进步不存在因果关系，说明H省的直接融资构成科技进步的必要条件，间接融资和金融业增加值并未能构成科技进步的必要条件。脉冲响应分析结果显示，直接融资对科技进步起到正向拉动作用，且正向作用时间较长。间接融资和金融业增加值对科技进步呈现正负双向的拉动作用，且正向拉动作用较小，持续时间较短，说明长期内直接融资对科技进步的影响较大，而间接融资以及金融业增加值对科技进步的促进作用有限。方差分解结果表明，就正向作用影响幅度和影响时间而言，对科技进步贡献程度最大的是直接融资，其次是间接融资，最后是金融业增加值。

通过上述分析可以看出，直接融资有力地拉动了科技进步，从而有效地促进了供给侧结构性改革；间接融资对科技进步具有一定的拉动作用，短期内在一定程度上对供给侧结构性改革有促进作用。而金融业增加值在整个过程中对科技进步、供给侧结构性改革并未起到明显的促进作用。

根据上述实证分析结果，提出如下建议：首先，应拓宽直接融资渠道。大力发展多层次资本市场，稳定主板市场，扩大中小板、创业板以及新三板市场。积极培育企业债券市场，鼓励有条件的大型企业发行企业债券，引导中小型企业发行集合债券。其次，应巩固间接融资渠道。在引导国有商业银行、股份制商业银行支持供给侧结构性改革的同时，积极发展城市商业银行、农村金融机构以及民营银行，鼓励多元化银行机构将资金更多地运用到供给侧结构性改革需要的地方。