基于自适应M-H采样的放射源定位算法

王明生，肖宇峰，刘 冉，刘 成2，杨 川

(1.西南科技大学 特殊环境机器人技术四川省重点实验室，四川 绵阳 621010；2.西南科技大学 国防科技学院，四川 绵阳 621010)

核工业设备在我国得到了广泛应用，据国家核安全局统计发布的最新数据，全国在用各类放射源 126991枚；各地方放射性废物库已收储废旧放射源 40341枚，国家放射源集中暂存库以及由生产厂家回收的废旧放射源共152109枚[1]。遗失的放射源会污染环境，严重威胁人们的身体健康甚至生命安全，快速准确的放射源定位与搜寻方法是核安全领域重要研究课题。

关于放射源定位方法，国内外都取得了不少成果。Sun等人[2]介绍了一种使用编码孔径相机的方法估计放射源位置，但其设备较重，使用范围有限。张译文等人[3]建立了基于多探测器单元的方向信息和计数信息的放射源定位和活度计算方法，用于区域内的放射源定位和活度监测。左国平等人[4]设计了一种三角圆筒铅屏蔽的NaI定位探测器，铅屏蔽层厚度影响角度分辨能力。Miller等人[5]介绍了一种定位方法，用于机载平台从空中大范围的放射源定位。Sharma等人[6]介绍了一种基于统计的网格细化方法定位放射源；Pahlajani等人[7]通过部署传感器网络确定放射源，两者适用于固定场景。Bai等人[8]采用最大似然估计方法定位放射源，没有利用放射源的先验信息。另外一些学者通过信号强度对射频标签进行定位[9-10]。

小型的个人剂量仪操作方便、使用灵活，是获取辐射信号强度的常用传感器；同时在放射源测量中存在着测量噪声以及先验信息不足等不确定因素，而概率统计是处理此类问题的有效方法[11]。基于此，建立放射源定位的贝叶斯推理模型，提出了改进的自适应M-H(Metropolis-Hastings)算法实现放射源的位置估计。使用Eu-152源设计实验，对改进前后的M-H算法实验结果进行了验证。

1 辐射测量中的贝叶斯模型

1.1 辐射测量原理

在均匀空气中，点放射源d处的剂量当量率H(μSv/h)根据文献[12]可由式(1)近似计算。

(1)

式中,A为放射源活度(MBq)；E为衰变时释放的伽马射线能量(MeV)；d为距离(m)。

式(1)可改写为H=I/d2，其中I=AE/6，可以看作在离源1 m处的剂量当量率。

在辐射测量中，可以探测放射源在单位时间内发射的放射性粒子数，该过程存在放射性计数统计涨落现象且服从泊松分布[13-15]。

(2)

式中，z∈N+为实测的每分钟计数值(min-1)，λ=Mη，M为理论计数值，η为探测器的效率，λ为期望计数值。z可表示为包含一个能量响应常数Energynumber的算式[12]，即z=H×Energynumber。

1.2 辐射测量中贝叶斯推理模型

根据辐射测量原理，对环境中未知放射源的检测，可用图1所示的平面示意图简单说明。

图1 放射源检测示意图

如图1所示，在辐射场内存在r≥1个未知的点源，源s(s=1,2,…,r)用参数向量θs=[xs,ys,Is]T∈R2×R+表示，(xs,ys)为放射源的平面坐标，Is为放射源1 m处辐照强度计数值，所有点源集合表示为θ=[θ1,θ2,…,θr]。gi=[xi,yi,zi]T∈R2×R+表示在该平面某位置(xi,yi)的一个测量点，zi为测量点处的计数值。i=1,2，…，m，表示不同的测量点。假设各测量点之间相互独立，观测向量集G=[g1,g2,…,gi]，则观测向量G的似然函数为

(3)

式中,p为式(2)定义的泊松分布。

p(gi|θ,r)=P(zi;λi(θ))

(4)

(5)

(6)

式(5)中，忽略空气介质的衰减，μb为背景辐射值。

假设放射源参数向量θ的先验分布为p(θ|r)，根据贝叶斯理论可得θ的后验分布为

(7)

式中，p(G|r)可视为常数，因此联合式(3)，式(7)可写为

(8)

得到后验分布p(θ|G,r)，估计放射源位置。以估计位置和真实位置的距离来评估放射源定位的精确度。

对于一般情形，点源的数量和位置都是未知的。除了定位放射源的位置，还要估计放射源数量。可采用渐进估计的方式，其后验概率计算公式为

(9)

在p(θ,r|G)基础上，可得到r个放射源概率的一般意义计算公式：

(10)

可得放射源数目r的MAP估计值为

(11)

放射源参数θ的MAP估计值为

(12)

本文主要研究r已知情况下的放射源定位。

2 自适应M-H采样的放射源定位算法

2.1 M-H采样算法估计放射源位置

马氏链蒙特卡罗(MCMC)模拟方法是从某一目标分布f(x)中抽取样本的一类方法。常用采样方法有Gibbs采样和M-H采样。Gibbs采样应用于多维分布的采样，需要满足的条件是：多维度分布中任意一个子分量关于其他子分量的条件分布已知，以此条件分布作为提议函数。在放射源位置估计问题中，条件分布p(xs|ys,Is,r)、p(ys|xs,Is,r)、p(Is|xs,ys,r)未知，无法使用Gibbs采样。而使用随机游走链的M-H采样，通常构造提议函数为正态分布函数，正态分布的性质由均值和标准差决定，更易于实现。

本文采用M-H算法，对放射源参数向量θ的后验分布p(θ|G,r)采样，然后对样本进行统计分析，间接得到后验分布p(θ|G,r)的统计性质，完成放射源位置估计，主要包括以下几个步骤。

(1) 初始化采样点，令t=0。

(2) 采样新粒子与更新粒子集，当t=1,2,…,n时。

① 构造提议函数。对于放射源参数θ，假设其Markov链中上一时刻状态为θt-1。构造以θt-1为均值，标准差为σ的正态分布为提议函数q(θ*|θt-1)～N(θt-1,σ2)，其标准差σ的选取是关键。

③ 计算新状态θ*的接受概率。将采样得到的新状态θ*通过式(8)计算p(θ*|G,r)。再根据式(13)，计算候选状态θ*的接受概率α。

(13)

假设θ中各分量相互独立,先验分布p(θ|r)为均匀分布，提议函数为正态分布，式(13)可简写为

(14)

④ 更新粒子集。以概率α接受候选状态θt=θ*，以概率1-α保持上一时刻状态不变θt=θt-1。

(3) 估计放射源位置。

对采样得到的粒子集θ=[θ0,θ1,θ2，…，θn]进行统计模拟分析，得到θ各分量粒子集的期望E(xs)和E(ys)，以期望值估计放射源位置。

2.2 自适应M-H采样算法估计放射源位置

采用随机游走链的M-H算法，其初始点和提议函数标准差对整个算法的收敛、效率都有较大影响，它主要的不足是这两者需要依靠人的经验来选取调整。如果取值不合适，算法执行的最终结果可能收敛缓慢甚至不收敛。

通常，将后验分布p(θ|G,r)附近的点为起点有利于在很短时间内就能得到有效的采样，提高算法效率。对于提议函数标准差的选择，也有不同的策略。一种策略是依据一条链的生成过程中对新状态的接受率来选择。根据文献[16]～文献[18]的研究，不同的接受率会使随机游动采样法的效率受到不同程度的影响。对于一维变量，最优接受率为0.44，将最大限度优化随机游动采样法的效率，大于五维以后会降为0.23左右，且与具体分布无关。

该阶段主要工作是得到一个采样起始点θ0，使其后验概率值p(θ0|G,r)大于阈值ρ(ρ≥0)，以此让采样的起始点靠近后验分布p(θ|G,r)附近，具体过程如下。

(2) 自适应调整提议函数标准差σ。

① 根据最优接受率0.23设置一个比较理想的范围，如区间 [β-ε,β+ε] (β=0.23，ε为容忍度)。以第(1)阶段得到的初始值θ0为采样起始点，给定标准差初始值σ0，生成一条长为的L的Markov链(实验部分L取值为3000)，即粒子集[θ0,θ1,θ2，…,θL]，记录粒子集中接受候选状态的次数为nnew。

② 估算接受比率Pn。

(15)

若P0∈[β-ε,β+ε]，则得到满足要求的标准差σ=σ0；反之，则以σ0为中心，τ为偏差做一次随机游动，得到一个新的标准差σ1，即σ1～N(σ0,τ2)。然后以同样的方法得到P1，以此类推计算P2,…,Pn。τ的计算为

τ=σn×(|Pn-β|÷β)

(16)

τ的计算依据是根据接受比率与理想值的接近程度进行调整。

在不断调整标准差的过程中，还应当考虑到此类情况，在第n次经过随机浮动后得到的标准差下，得到的接受率Pn比上一次得到的Pn-1(n>2)更远离理想区间，即|Pn-β|>|Pn-1-β|，在这种情况，说明新得到的标准差σn不如上一次得到的σn-1理想，是应当舍弃的，同时接下来的调整应当在两次中相对更好的条件下进行，也就是保留上次结果，置σn=σn-1，Pn=Pn-1，然后继续下一轮调整，直到求得满足接受率的标准差σn为止，保存标准差σ=σn。

(3) 执行M-H算法估计放射源位置。

以第(1)阶段中得到的θ0为初始值和第(2)阶段中得到的σ为标准差，执行M-H算法对放射源参数θ的后验分布p(θ|G,r)实施采样，对采样的粒子集θ=[θ0,θ1,θ2，…，θn]进行统计模拟分析，得到θ各分量粒子集的期望E(xs)和E(ys)，以期望值估计放射源位置。

3 实验验证及其分析

3.1 单放射源定位实验

为验证上述算法的可行性和有效性，设计如下实验：在13 m×19 m的大厅，建立笛卡尔坐标系。采用1枚活度约为370 MBq的Eu-152放射源，以北京核仪厂的BH3084型个人剂量仪为探测器进行实验。

将放射源完全暴露在空气中，实验选取9个随机测量点，每个测量点测量时间为2 min，待读数稳定，用同一个仪器测三次取平均值。放射源真实坐标为(4.8 m,4.8 m)，测量结果见表1。

表1 实验测试点及剂量率

使用Matlab编程实现M-H算法和自适应M-H算法，对实验采集的数据进行处理。可设放射源位置为x∈[1,5]、y∈[1,5]上的均匀分布，迭代4500次。如图2所示，给出了M-H算法和自适应M-H算法的采样轨迹图，从图2(a)中可以看出M-H算法在迭代约500次后进入平稳状态，能估计出放射源位置。但样本路径混合性能较差，表现为在真值附近波动小，没有对待估变量的支撑域进行充分采样。在相同初始条件下，依据2.2节的描述，设置自适应M-H算法中接受率容忍度ε=0.05。ρ通常是一个很小的值，取较大值表明采样初始值靠近后验分布附近，但计算量大，本文取ρ=2×10-10。w的值根据采样空间大小决定，目的是消除采样随机性，减少极端采样值的影响，文中取w=10。从图2(b)中可以看出自适应M-H算法约迭代100次后进入平稳状态，其收敛速度约为M-H算法的5倍。同时采样的样本具有良好的混合性能，表现为在支撑域附近剧烈的震动，在真值附近进行充分的采样。

图2 采样轨迹图

表2给出了实验中使用的初始值θ0、提议函数初始标准差σ0和改进前后两种算法的统计结果，可得M-H算法的估计误差为0.26 m，自适应M-H算法的估计误差为0.17 m。改进后的自适应M-H算法估计结果更为准确。

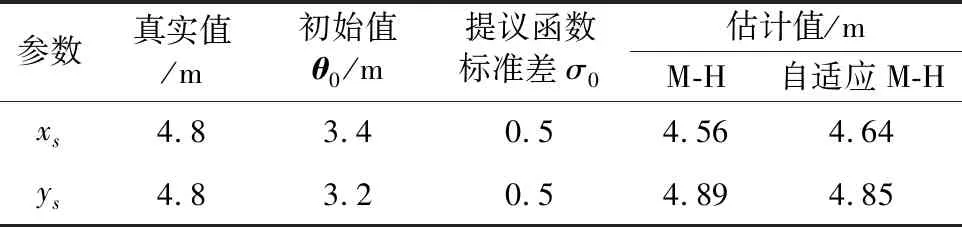
表2 估计结果统计

此外，还希望得到的样本是独立的，为检验样本间的自相关性，如图3所示，给出了两种算法得到的样本自相关系数图。在图3中，M-H算法得到的样本自相关曲线，下降较为平缓，说明样本间有较大的自相关性，得到的样本集中独立的样本数较少，算法效率不高。也说明在轨迹图(见图2(a))中，样本曲线在真值附近波动小的原因，采样不够充分。自适应M-H算法得到的样本自相关曲线具有很陡的下降曲线，说明得到的样本集中样本间自相关性小，采样更充分，表明与M-H算法取得相同长度的Markov链中包含有更多的独立样本，算法效率更高。

图3 样本自相关系数图

3.2 双放射源定位实验

同单放射源定位实验的场地和条件，使用2枚活度约为370 MBq的Eu-152放射源，将其中一枚放入铅罐，分别放置在s1(4m,4.8m)和s2(4.8m,4.8m)进行实验，测量结果见表3。

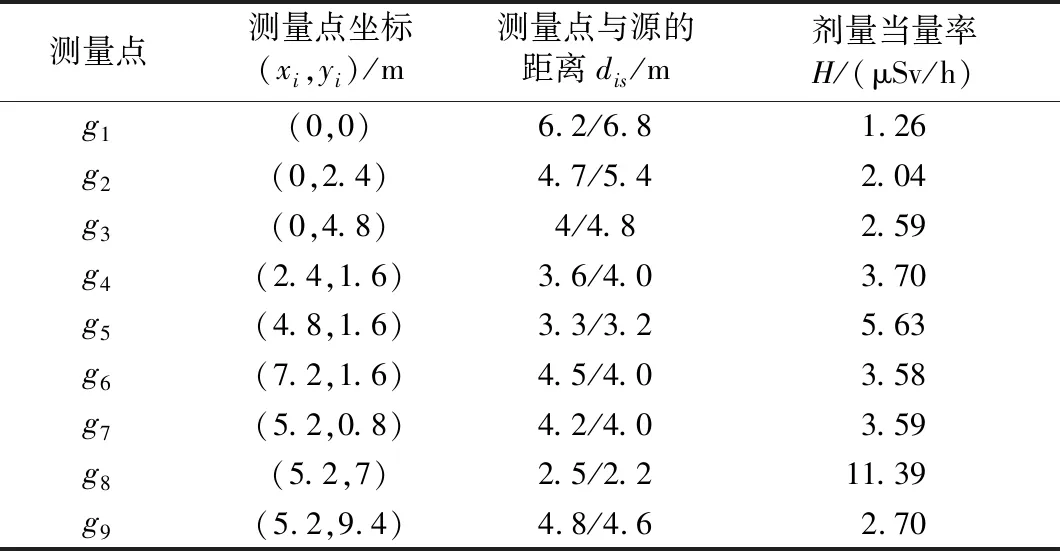
表3 实验测试点及剂量率

单放射源定位实验已经证明了自适应M-H算法具有更好的定位效果，所以直接使用自适应M-H算法对双放射源定位实验采集的数据进行处理。具体的分析过程同单放射源实验，限于篇幅，不在赘述，

样本直方图可以直观表现出对各空间位置的估计，图4给出了迭代6000次的采样结果统计直方图。图4(a)中拟合的正态曲线均值，即统计结果为(3.7 m,4.9 m)、图4(b) 中拟合的正态曲线均值，即统计结果为(5.0 m,4.9 m)，可分别对应于放射源s1和s2，能够完成双放射源的定位，证明了定位方法对多源的有效性。

图4 样本统计直方图

4 结束语

定位点放射源是一个非常有挑战的课题，而使用轻量级的传感器结合有效的算法是一个重要的研究方向。 实验结果表明：在室内，使用相对便宜的个人剂量仪，采用贝叶斯理论结合统计模拟方法能够较好地定位点放射源。所提出的自适应M-H算法能对点放射源位置估计量的初始值和提议函数的标准差进行自适应调整，在效率和收敛速度方面都优于M-H采样方法。下一步研究工作主要针对未知数量的多源、有障碍物情况下的点放射源定位。