基于Laguerre函数的BLDCM转速预测控制器

郭 伟1,，姜 睿，李 涛1,，高严凯

(1.大气环境与装备技术协同创新中心，江苏 南京 210044； 2.南京信息工程大学 自动化学院，江苏 南京 210044)

无刷直流电机(Brushless DC Motor,BLDCM)因具有结构简单、运行效率高等优势，在精密机床、汽车电子、航空航天等领域得到广泛应用[1]。传统BLDCM控制器多基于线性理论设计，但由于模型中存在R、L等慢时变参数，故解耦简化得到的模型势必不能满足不同工况调速的需求[2]。

针对上述问题，许多学者将自适应机制引入控制器设计中，将非线性时变参数看作扰动项，设计自适应观测器或滤波器进行估计[3-5]，但大多会假设未估计量变化率为零，且观测器本身会带来系统延迟，这都会影响参数辨识精度，进而导致控制误差。因此，可根据实时信息在线辨识模型参数的控制器设计显得尤为重要。

近年来，随着微处理器(如DSP、FPGA等)性能的大幅提升，预测控制算法在电力电子和电机驱动领域得到广泛关注[6-7]，设计简单、动态性能好等特点使该方法成为电机控制领域最有可能替代PI算法的控制方案[8]。文献[9]用电流预测控制器替代了传统PI电流调节器，有效抑制了电流纹波。GPC作为一种结合自校正思想的预测控制算法[10]，具有建模与控制于一体的特点，自Clarke提出以来30多年，已有众多学者对其进行了改进优化。文献[11]从预测模型着手，利用ARMAX模型描述动态对象，并在此基础上推导得出可直接求解控制量的广义预测控制器。文献[12]将优化后的广义预测控制应用于无刷直流电机速度控制中，并在DSP实验箱中进行了算法验证，证实该算法在快速系统中应用的可行性。针对原始GPC和文献[11]中所提算法需引入丢番图方程求解计算量大的问题，文献[13]利用递推的方法得到预测模型，求解过程简单，更易于硬件实现。文献[14]将ARMAX模型转换成状态空间方程形式，并将Laguerre函数引入来解决传统模型预测控制不能保证无差拍控制的缺点。

调速性能和转矩波动一直是衡量BLDCM运行性能的两个重要指标，本文主要研究BLDCM控制系统的调速性能。为进一步减小算法计算量，满足电机控制实时性要求，本文在文献[13]提出的简化GPC基础上，引入Laguerre函数对控制增量进行参数化，针对传统GPC算法普遍存在超调的问题，借鉴文献[18]中修改性能指标的思想，以期结合PI算法的优势，提出了一种新型的控制算法，最后将其应用在BLDCM转速跟踪控制中，并与文献[13]所提算法进行比较。Matlab平台仿真结果表明，相比文献[13]提出的算法，该算法对跟踪指令响应更快，超调小，抗干扰能力强，对参数不确定性具有较强的鲁棒性。

1 BLDCM模型

传统BLDCM控制策略为双闭环控制结构，内环电流环主要作用为限制电流，保证系统稳定运行[15]。实际应用中，转速单环控制器已能满足绝大多数运行情况[16]，故本文采用单环控制器，在此推导BLDCM空载运行时的传递函数[1]。

以A、B导通为例，不计换相暂态过程，则有

(1)

式中，Ud为直流母线电压；ra为绕组线电阻，ra=2R；La为绕组等效线电感，La=2(L-M)；ke为线反电势系数。

由电机运动方程可得空载情况下的电枢电流为

(2)

式中，KT为电机转矩系数；J为转子转动惯量；Bv为黏滞摩擦系数。

将式(2)代入式(1)中，并做Laplace变换可得BLDCM传递函数为

(3)

因有Ω=2πn/60，故机械角速度与转速之间呈线性关系，其中转速n单位为r/min。

2 控制增量Laguerre化的预测控制

2.1 离散Laguerre函数

连续型Laguerre函数是平方可积函数空间L2(0,∞)上的一组正交基，将其z变换离散化后可写为[17]

(4)

式中，a为离散Laguerre函数的极点，0≤a<1。

注意到有如下递推关系:

(5)

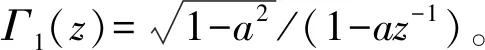
用l1(k)表示Γ1(z)的z逆变换，则有

L(k)=[l1(k),l2(k),…,lN(k)]T

那么式(5)满足

L(k+1)=ψL(k)

(6)

且有

(7)

式中，ψ为N×N的矩阵；β=1-α2。

2.2 改进的广义预测控制

被控对象ARMAX模型可表示为[13]

(8)

式中，y(k)、u(k)和ξ(k)分别为输出、控制和白噪声，d+1为时滞；其中参数可由下式递推得出：

(9)

式中，n=min{w-1,na}。

预测模型为

Y=Ym+GΔU

(10)

Y=[y(k+d+1|k),y(k+d+2|k),…,y(k+p|k)]T
Ym=[ym(k+d+1),y(k+d+2),…,y(k+p)]T
ΔU=[Δu(k),Δu(k+1),…,Δu(k+p-d-1)]T

(11)

式中，p为预测长度。其中，

需要注意的是，令式(9)第二个式子中i=0可快速递推出矩阵G中元素。

极小化性能指标

(12)

式中，λ为控制加权系数；参考轨迹Yr计算具体见文献[19]。

由∂J/∂ΔU=0可得

ΔU=(GTG+λI)-1GT(Yr-Ym)

(13)

则即时控制增量为

Δu(k)=fT(Yr-Ym)

式中，fT=[1 0 … 0][GTG+λI]-1GT。

由此可得控制量为

游客们对三峡地区历史文化的认知主要是巴蜀文化和巫文化。原始的巴人部落、舞蹈表演和神秘的巫文化祭祀活动构成了游客们对三峡地区古代文明的体验，帮助游客更好地理解遥远的历史文化。一位广西的年轻游客描述了印象深刻的巫文化祭祀表演：

u(k)=u(k-1)+Δu(k)

(14)

相比于Clarke提出的原始形式广义预测控制算法，该算法的预测模型计算借鉴了动态矩阵控制，无需引入丢番图方程，求解过程更加简洁，编程易实现。

2.3 控制增量Laguerre化的PI型广义预测控制

算法最终会在嵌入式场合实现，为进一步减小算法计算量，本文将离散Laguerre函数引入上述算法，并与PI型性能指标结合。

在k时刻，控制增量轨迹Δu(k)，Δu(k+1)，…，Δu(k+j)可以看作是一个稳定动态系统的脉冲响应，因此，可将Laguerre函数应用于控制增量的参数化设计，即利用l1(k)，l2(k)，…，lN(k)捕获一系列与系统脉冲响应有关的系数c1，c2，…，cN[17]。与预测函数控制类似，该函数的引入使得算法对控制量的求解从控制量本身转移到了组合系数的优化，由于这些系数个数少且与预测长度无关，因而可以减少在线优化的计算量[10]。

控制增量Laguerre化过程如下

(15)

式中，L(j)=[l1(j),l2(j),…,lN(j)]T；η=[c1,c2,…,cN]T。

设定参考轨迹与预测输出间误差为

e(k+j)=yr(k+j)-y(k+j|k)

则有

Δe(k+j)=e(k+j)-e(k+j-1)=Δyr(k+j)-Δy(k+j|k)

工业控制中常选取PI型性能指标[18]，故本文修改性能指标如下：

ki(j)e2(k+d+j)+r(j)Δu2(k+j-1)

(16)

式中，kp(j)、ki(j)和r(j)分别为输出误差和控制增量加权系数，假设为常数kp、ki和r。

为推导方便，将该性能指标改写成矩阵形式

(17)

定义L=[L(0)T,L(1)T,…,L(p-d-1)T]T，则控制增量可写为

ΔU=Lη

(18)

将式(18)代入式(17)，由最小二乘法可得

(19)

式中，μ=LTGTHGL+LTRL；β=LTGTH+LTGTHT；H=TTKpT+Ki。

因而可得即时控制量为

u(k)=u(k-1)+Δu(k)=u(k-1)+L(0)Tη

(20)

当对象参数(式(8))未知时，可采用渐消记忆最小二乘法进行参数估计[19]，很多情况下，由于在线辨识的复杂性，用参考轨迹实现反馈校正。

采用上述算法设计BLDCM转速控制器，控制系统结构框图如图1所示。

图1 控制系统结构框图

3 仿真结果与分析

将电机空载运行时采集到的输入输出数据导入Matlab系统辨识工具箱，可得被控对象为[20]

y(k)-0.4288y(k-1)-0.5665y(k-2)=

1.875u(k-1)-1.87u(k-2)+ξ(k)

式中，ξ(k)为方差为0.01的白噪声。

为验证新型算法的可行性，在Intel酷睿i7处理器、64位8 GB系统、Matlab版本R2016a的环境下进行仿真，仿真总时长0.063 s。所提出的算法参数选为：预测长度p=3；Laguerre函数参数a=0.2，N=5；加权矩阵Kp=Ki=diag{0.2,0.2,0.2}，R=diag{0.5,0.5,0.5}；柔化系数α=0.7。

下面对电机在变速、受扰和模型失配3种工况下的控制性能进行比较。

图2为文献[13]改进GPC与所提出的算法在调速性能上的比较。电机起动时转速设定值为2500 r/min，在0.2 s时设为2000 r/min，由图1可知，新型算法在起动时几乎无超调，控制增量在0.012 s迅速收敛至零，且跟踪转速更为迅速，变速运行时依旧能保持很好的跟踪性能。

图2 调速性能比较

图3、图4为4种算法下抗干扰能力的比较。由图可知，电机起动时，4种算法中GPC_Laguerre_PI响应最快，GPC_Laguerre紧跟其后，GPC_PI次之，最后则是改进GPC算法。在0.2 s时给系统加入扰动，GPC_Laguerre波动之后能迅速恢复到设定转速，GPC_Laguerre_PI抗干扰能力与之相当，最后则是GPC_PI。

图3 抗干扰能力比较(转速分析)

图4 抗干扰能力比较(控制增量分析)

图5为4种算法在模型失配情况下的控制性能比较。由图可知，GPC和GPC_PI两种算法受预测模型失配影响非常大，而控制增量Laguerre化后的两种改进GPC算法则几乎不受该工况影响。其中，模型失配时，GPC_Laguerre_PI算法控制效果最好。

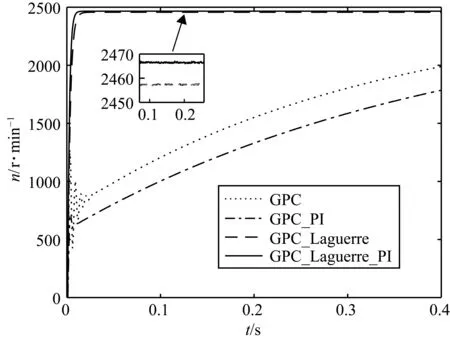
图5 模型失配比较

图6为Laguerre函数中a参数变化的比较。由图6可知，当a=0.8时，系统响应最快，但存在抖动，实际中不利于电机控制。当a=0.2时，虽响应较慢，但控制器可以准确跟踪设定转速值2500 r/min，因此本文调参时选用a=0.2。

图6 Laguerre函数参数a变化比较

4 结束语

本文在改进GPC算法基础上引入Laguerre函数对控制增量进行参数化，使系统响应更迅速；通过修改PI型性能指标，抑制了超调，得到更好的稳定性。用改进后新型的控制算法设计了无刷直流电机转速单环控制器，并在Matlab平台进行验证。仿真结果表明，该算法具有良好的控制品质。本文减少了电流环对最大电流的限制，若能将电流约束引入算法推导中，还需结合优化算法做进一步的研究。