制动片结构变化对系统不同频段稳定性的影响

林梅彬

(福州职业技术学院 交通工程系， 福州 350108)

汽车盘式制动器结构的优化设计一直以来是汽车行业研究的热点问题，不合理的制动器结构设计可能导致汽车在制动过程中产生不稳定振动，进而产生刺耳的制动尖叫噪声。这些制动振动噪声的存在将严重影响驾驶的舒适性和制动稳定性[1]。由于制动噪声是制动盘和制动片之间的摩擦动态不稳定造成的，因此可以根据噪声频率的不同将其分为3类：0～1 000 Hz的低频颤振噪声、1 000～8 000 Hz的中频尖叫噪声和8 000 Hz以上的高频尖叫噪声[2]。

目前国内外对制动器进行结构仿真分析的文献比较多，且大多集中在振动模态分析、热应力分析以及制动噪声分析等方面[3]。Shin等[4]建立两自由度模型来研究盘式制动器系统产生不稳定振动的基本机制，并论证了抑制其不稳定振动的必要条件。李清等[5]利用ANSYS软件建立盘式制动器有限元模型，计算分析了制动器各部件的振频现象，并深入研究了不同零部件及其参数对结构制动稳定性的交叉影响，结果表明：在一定范围下改变钳体和制动盘的厚度能提高制动器的稳定性。此外，许多学者采用复特征值分析法研究了不同制动片结构对制动系统不稳定性的影响，结果证明制动片结构的变化将会改变系统的本征频率和模态耦合现象，进而改变系统的稳定性[6-8]。虽然这些研究结果均表明制动器结构变化对系统的稳定性及耦合状态产生影响，但是它们并没有系统性地对结构变化和不稳定振动的频段进行划分，不同结构的制动器系统在制动过程中是否可以抑制或增加某些频段的不稳定模态及频率亦没有系统性地讨论和研究。因此，开展制动器结构变化对系统不同频段影响的研究具有重要意义和创新性。

如今，许多制动片生产商在摩擦材料表层进行开沟倒角处理，用于改善制动系统的稳定性及热挥发特性。但是，关于制动片这些结构变化和制动器不稳定振动频段之间的关系并没有得到系统性的研究。本文利用有限元软件Abaqus/Standard处理器研究了制动片结构变化对汽车在制动过程中不同频段的稳定性的影响，探寻能提高制动器稳定性的结构优化参数值，为提高汽车制动器安全性及稳定性设计提供理论依据。

1 方法和数值模型

1.1 复特征值分析方法

汽车盘式制动器的制动过程主要依靠制动盘和制动片之间相互接触产生的摩擦阻力来达到减速刹车效果，其运动方程表示为[9]：

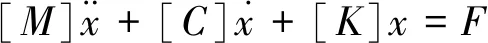
(1)

式中： [M]、[C]、[K]分别为制动器系统的质量矩阵、阻尼矩阵、刚度矩阵；x为振动的广义位移向量；F为制动盘和制动片接触面的摩擦力，可简化为以下形式[9]:

F=⎣Kf」x

(2)

式中：⎣Kf」为摩擦接触刚度矩阵。将式(2)代入式(1)，得

(3)

式(3)中由于引入了摩擦力将导致系统的刚度矩阵出现非对称，这意味着该线性系统的雅克比矩阵存在复特征值。式(3)的特征方程可以表示为

{λ2[M]+λ[C]+([K]-[Kf])}φ=0

(4)

式中：λ和φ分别为方程(4)的特征值及对应的特征向量。系统第i阶的复特征值λi为

λi=ai±jwi,i=1,2,…

(5)

式中：ai为复特征值实部，wi表示系统的不稳定程度；为复特征值虚部，代表系统的不稳定振动频率。当复特征值实部大于0时，表示摩擦系统处于负阻尼状态[10]，系统由于能量的馈入将发生不稳定振动，此时相应虚部则为系统不稳定振动的模态频率。

为使摩擦系统在各不稳定振动频率处的不稳定程度具有可比性，定义复模态阻尼比εi作为评价指标[11]:

(6)

如果阻尼比为正，阻尼消耗能量，系统是一个典型的振动衰减系统，是稳定的。如果阻尼比为负，系统中不断有能量馈入，摩擦系统失稳，并形成持续的不稳定振动。

1.2 有限元模型

汽车盘式制动器是由制动盘、摩擦材料、背板及卡钳、活塞等多个零部件组成的系统，但不同零部件对系统稳定性的影响程度各有不同[11-12]。为减少计算量、提高计算效率，同时又能真实精确地预测和分析制动器系统的不稳定模态及频率，故简化的有限元模型由制动盘、制动片及制动背板3个关键零部件组成[6]。

本文利用Abaqus有限元软件建立如图1所示的简化制动器有限元模型，各零件实体均采用C3D8I单元类型划分网格，并选择advancing front网格算法来保证计算准确性。该模型共划分成2.138 2×104个实体单元，3.532 6×104个节点。制动盘与制动片之间为库伦摩擦接触形式。根据汽车实际制动工况及条件对简化有限元模型进行边界条件及制动压力、旋转速度等参数的设定，然后提交Abaqus/Standard处理器计算系统复模态及不稳定频率。

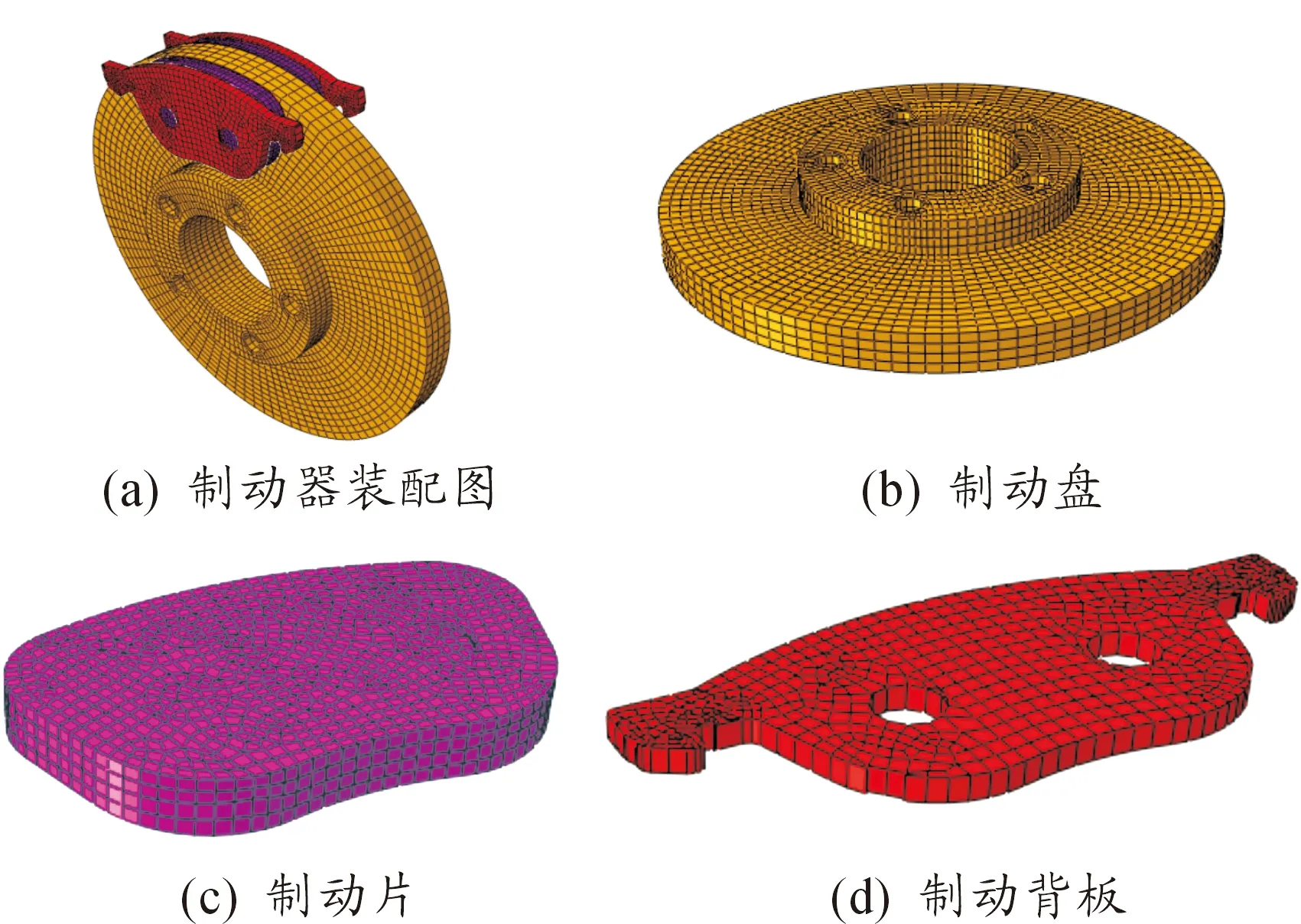
图1 盘式制动器简化有限元模型

Abaqus/Standard进行复特征值分析包含以下4个步骤：① 非线性静态分析，即对模型施加制动压力；② 非线性静态分析时对制动盘施加转速；③ 提取系统本征频率及模态振型；④ 结合摩擦耦合作用进行复特征值分析[12]。

1.3 制动器模型复特征值

通过对图1所建的简化盘式制动器三维有限元模型进行复特征值分析计算，设置常值摩擦因数为0.3，得到制动片表面未经加工处理下的制动系统复模态特征值仿真结果，系统所有不稳定振动模态及频率如图2所示。由图2可知：盘式制动器系统的不稳定模态主要表现为制动盘沿面外的弯曲振动模态，系统不稳定模态的复特征值实部均为正值，表示摩擦系统会发生不稳定振动，其相应虚部表示系统的模态频率，即制动系统主要存在5个不稳定模态且失稳频率分别为：2 647.8、5 785.3、8 188.7、9 935.1和1 1465.4 Hz，其中包含2个中频尖叫噪声频率(2 647.8 Hz和5 785.3 Hz)以及3个高频尖叫噪声频率(8 188.7、9 935.1和11 465.4 Hz)。

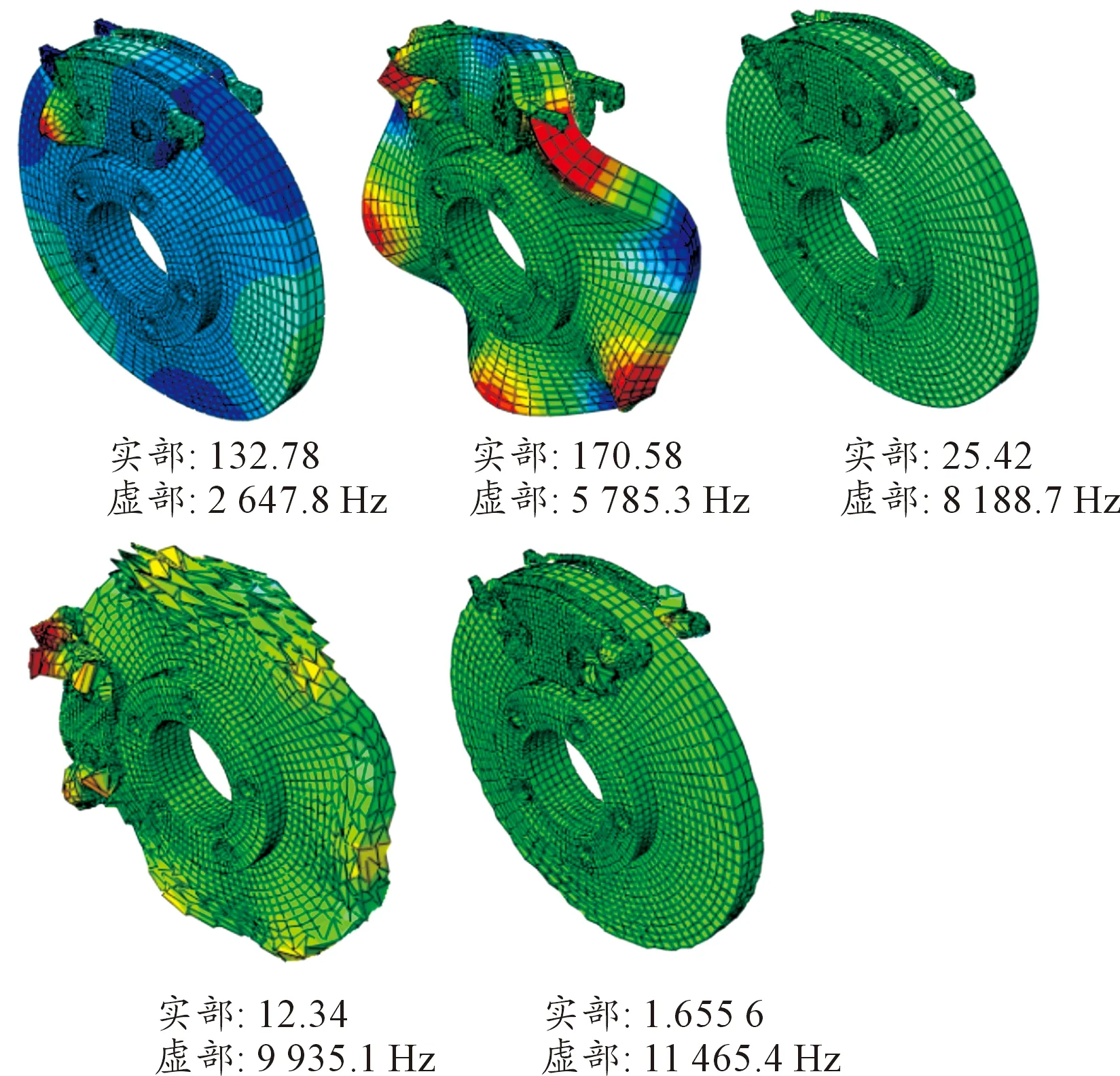
图2 制动系统不稳定模态及频率

2 结果和讨论

图3所示为制动片经过加工倒角和沟槽改变后的三维立体模型。图3(a)为表面两侧经过倒角处理的制动片，本文中选取10°、20°、30°和40°四组角度的倒角进行研究。图3(b)表示在制动片表面加工中间垂直单沟槽，沟槽深度为1.5 mm，选取2、4、6和8 mm这4组数值的沟槽宽度为研究对象。以制动片中心为沟槽旋转中心，中间垂直线为起始线，沿制动盘转动方向相同的沟槽角度记为“+”，与转动方向相反的沟槽角度记为“-”，其中沟槽宽度为3 mm，深度为1.5 mm，角度大小分别取10°、30°和50° 3组数值，其示意图如图3(c)和(d)所示。

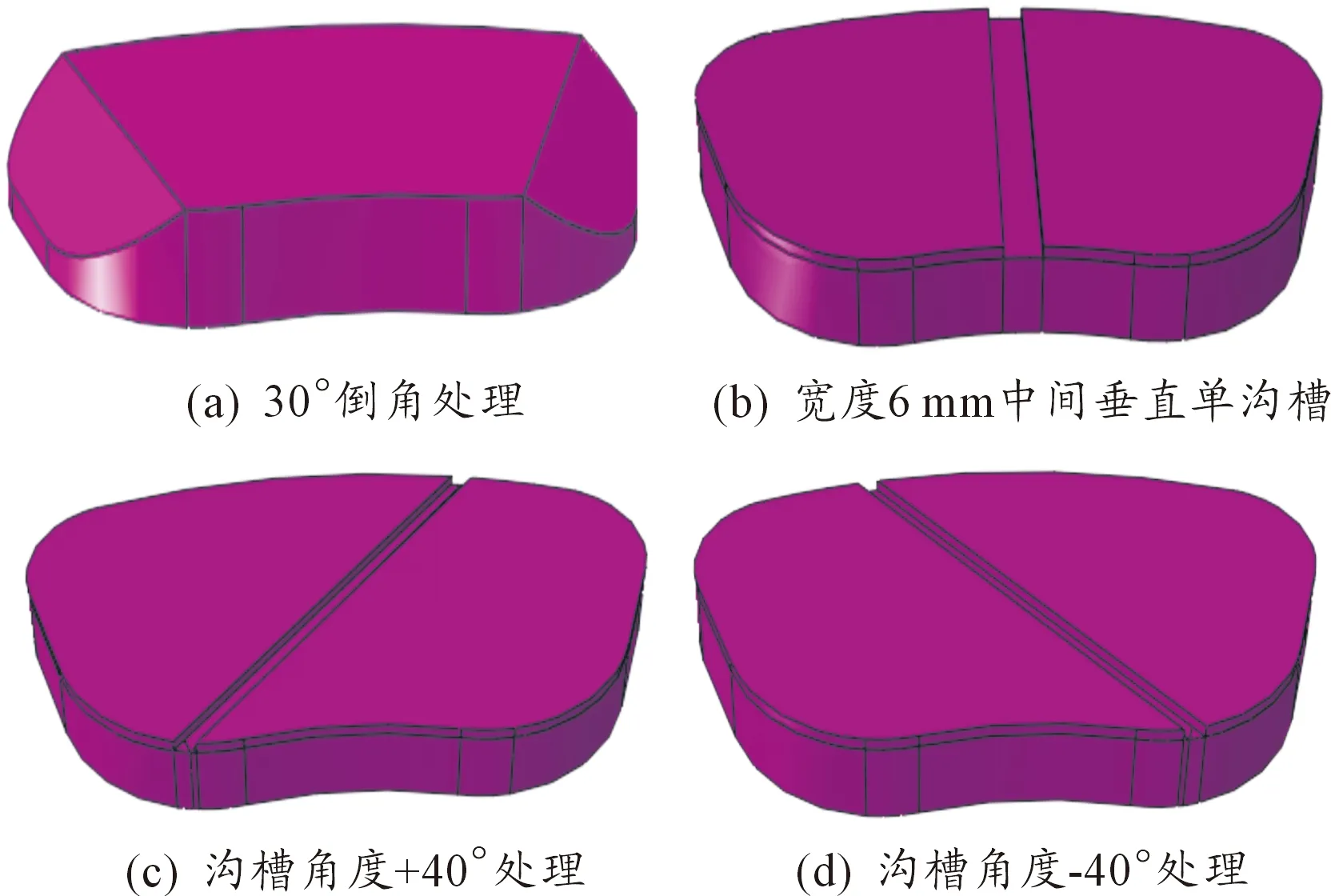
图3 制动片不同结构变化

2.1 倒角角度变化对系统不稳定模态频率的影响

图4所示为盘式制动器系统的不稳定模态频率和阻尼比随制动片上不同倒角角度的变化情况。

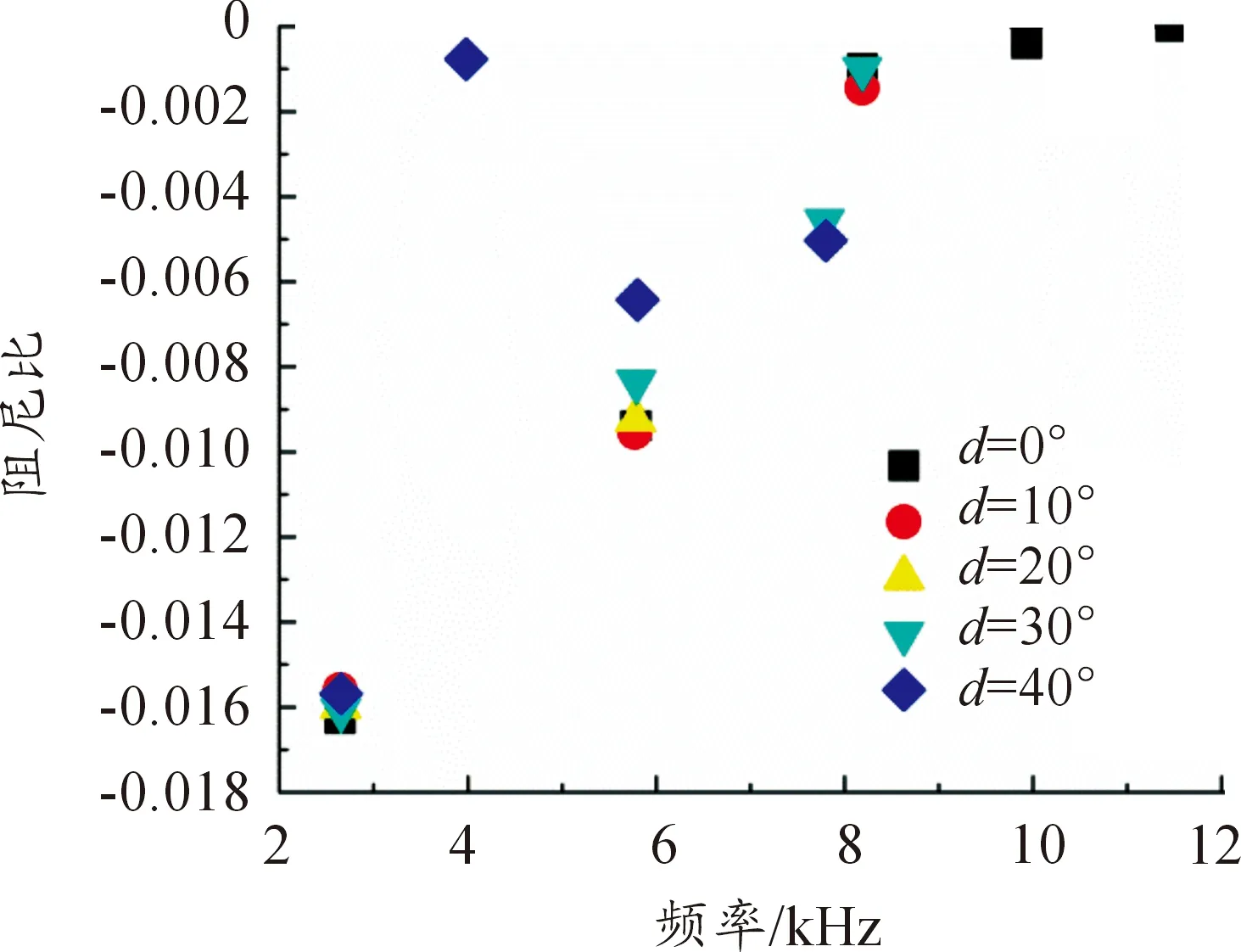
图4 系统阻尼比及不稳定频率随倒角角度变化

由图4可知：与光滑表面制动片相比，30°、40°倒角共有4个不稳定频率，虽使系统中频尖叫噪声频率的个数增加，但都能完全消除掉8 500 Hz以上的高频尖叫噪声频率，且40°倒角效果更佳；对于存在3个频率的10°倒角制动片而言，能够有效抑制在光滑制动片状态下出现的8 500 Hz以上的失稳模态频率；效果最为理想的是20°倒角，只有2个不稳定频率，且6 000 Hz以上的中高频频率则被完全消除。这表明制动片上倒角角度的变化将改变系统不同频段的不稳定模态频率，且当倒角角度为某特定值时，抑制系统不稳定频率效果更佳。此外，可以看出，进行制动片倒角处理的制动系统，其阻尼比值相比较光滑表面的值要小，意味着系统不稳定程度更小，系统稳定性增强。

2.2 沟槽宽度变化对系统不稳定模态频率的影响

通过在制动片表面中间开垂直单沟槽，数值分析研究了制动片上沟槽宽度变化对系统模态复特征值的影响，结果如图5所示。与光滑表面相比，在制动片表面开沟槽处理可以明显降低制动器系统在8 500 Hz以上的高频不稳定模态频率，证明了制动片上沟槽与系统失稳频率存在相关性。其中2 mm和4 mm沟槽存在3个不稳定模态频率且基本没变化。由图5可知：6 mm沟槽只有2个频率且都低于6 000 Hz，且阻尼比值是相对最小的，这表明在制动片上开宽度为6 mm的沟槽不仅可以完全消除6 000 Hz以上不稳定模态的中高频频率，还能很大程度上降低制动器系统发生模态耦合倾向性，从而提高盘式制动器的稳定性和制动效果。

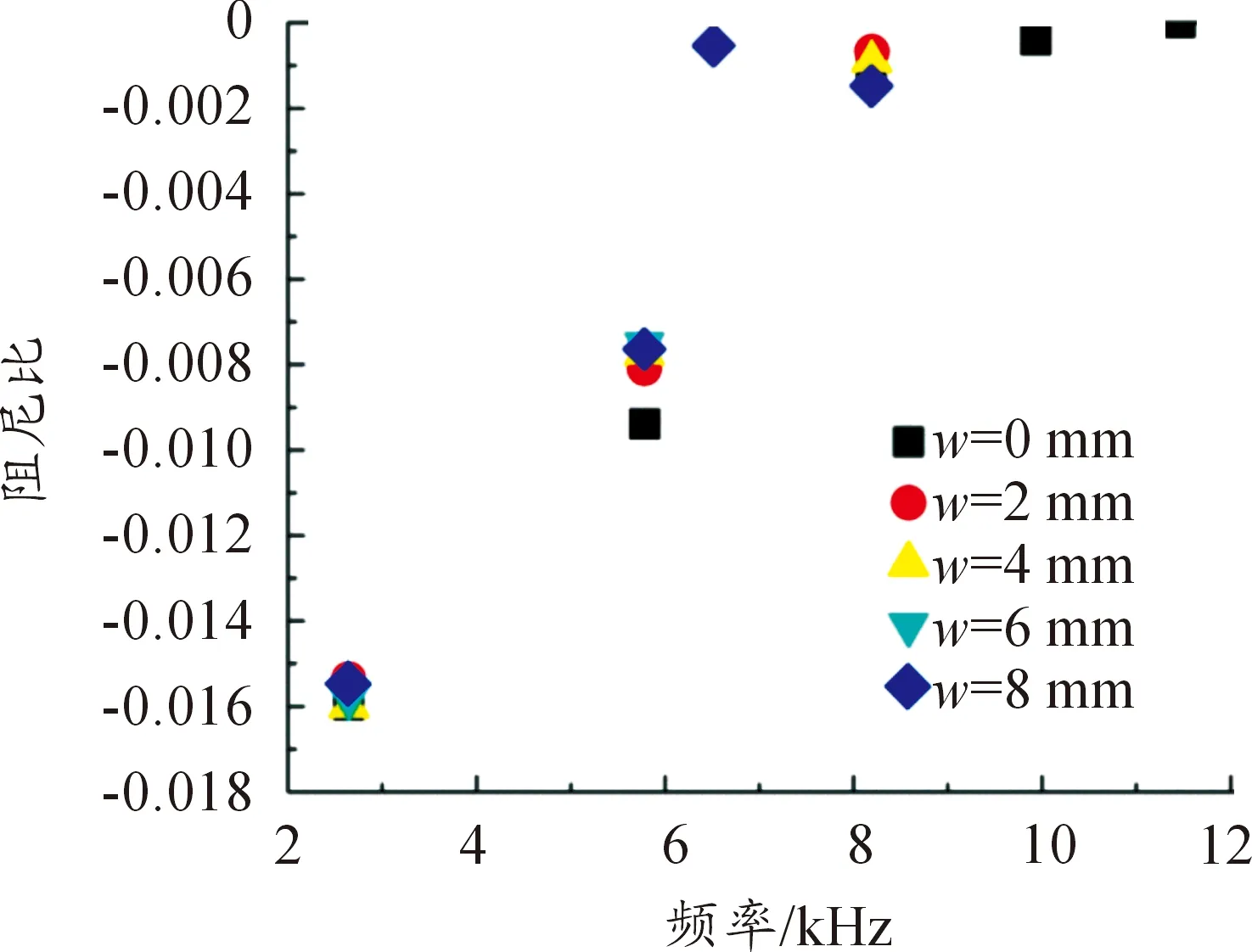
图5 系统阻尼比及不稳定频率随沟槽宽度变化

2.3 沟槽角度变化对系统不稳定模态频率的影响

从图6可以看出：在制动片表面加工与制动盘旋转方向相同的沟槽角度能够有效抑制住制动器系统8 500 Hz以上的高频尖叫噪声频率且系统阻尼比值会变小，表明开沟槽处理对于降低制动系统不稳定性有一定作用。其中+50°的沟槽还能有效消除光滑表面6 000～8 500 Hz范围内的中高频不稳定频率，+10°、+30°的沟槽则对8 500 Hz以下的不稳定模态频率影响效果不大，这说明当沟槽角度为某定值时能更大程度地消除系统不稳定模态及一定范围内中高频尖叫频率。

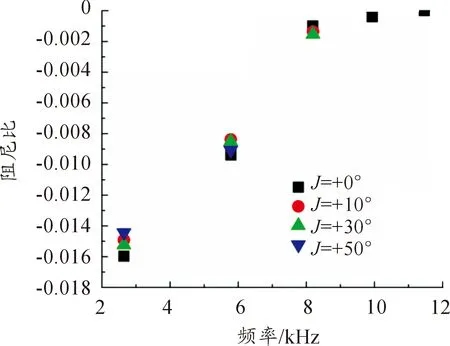
图6 系统阻尼比及不稳定频率随沟槽“+”角度变化

图7所示为系统的不稳定模态频率和阻尼比随制动片表面角度为“-”的沟槽的变化情况。同角度为“+”的沟槽的作用情况基本相似，-10°、-30°、-50°的沟槽亦可以消除8 500 Hz以上的系统振动模态频率，且-50°沟槽效果最佳，亦仅有2个失稳模态频率，频率在6 000 Hz以上的不稳定模态能被有效抑制。综上所述可以发现：在制动片表面沿2个不同方向开沟槽都能有效抑制或消除系统一定范围内的不稳定振动模态和频率，尤其当沟槽角度为某特定值时效果会更加理想。

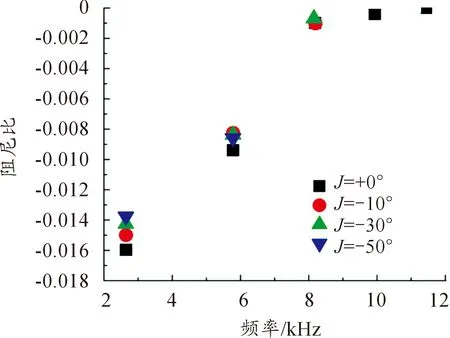
图7 系统阻尼比及不稳定频率随沟槽“-”角度变化

为进一步研究制动片上沿2种不同方向开沟槽对系统不稳定性的影响，将这6组沟槽角度分别进行两两对比，结果如图8所示。虽然同等大小沟槽的系统振动模态频率值基本一样，但角度为“-”的沟槽的阻尼比值要明显小于角度为“+”的沟槽，这表示沿与制动盘转动相反方向加工的沟槽能产生更小的不稳定系数，系统发生不稳定振动的倾向性更小，盘式制动器在工作过程中会更加稳定。

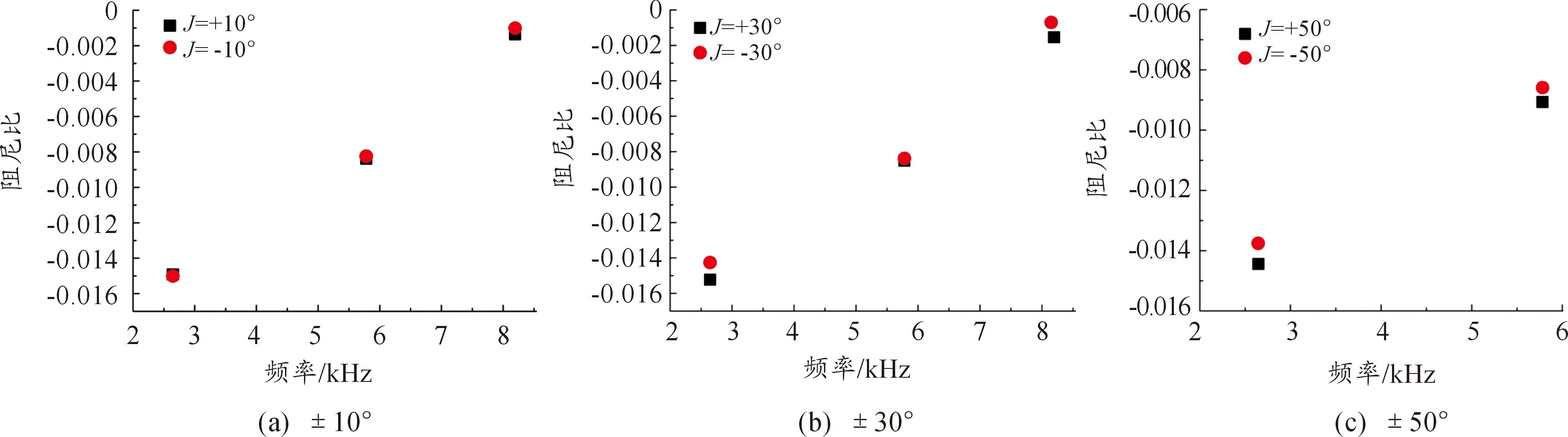
图8 2种沟槽角度方向对比

3 结论

本文通过对汽车盘式制动器简化有限元模型进行Abaqus有限元复特征值分析，预测和研究了制动片不同结构变化对制动系统振动稳定性及不稳定模态频率范围的影响。结果表明：

1) 在制动片表面加工倒角、沟槽等处理对系统不稳定模态很大的影响；

2) 不同的倒角角度、沟槽宽度、沟槽角度可以有效地降低、抑制或消除盘式制动器系统内一定范围的中高频不稳定频率，且当制动片上的倒角和沟槽取某些特定参数值时，系统发生模态耦合的倾向性更小，系统的不稳定程度更低；

3) 沟槽角度方向与制动盘旋转方向相反时，系统阻尼比值要明显小于方向相同的沟槽角度，故盘式制动器系统在工作过程中稳定性会更好。制动片不同结构变化对系统稳定性的影响可为汽车盘式制动器稳定性及结构优化设计提供一定理论依据和指导。

4) 对沟槽宽度、倒角角度等参数进行优化，通过响应曲面方法、正交试验法或者其他优化方法可以得到改善系统振动噪声某一特定频率的最优值，为优化设计提供理论依据。