基于灰色马尔科夫的地铁火灾逃生最优路径规划及3D模拟

张先华，李 政，谭小慧，王 康

(首都师范大学 a.信息工程学院; b.管理学院， 北京 100048)

地铁作为出行最为便捷、经济和高效的一种交通工具，广泛服务于大中城市。随着地铁成为人们出行越来越重要的交通工具，其安全问题也越来越受关注。地铁在带给城市人群便捷交通的同时，也存在许多不安全因素。由于地铁内环境封闭，大多数乘客对所处的环境不熟悉，这给突发火灾时的人员疏散带来巨大的安全隐患，容易引起群体恐慌，发生踩踏事故，甚至造成严重伤亡。

不同于地面建筑，地铁绝大部分线路和车站都在地下，空气流动只能依靠通风设备，地铁车站近乎为一个封闭的空间。由于大多数地铁乘客是不熟悉地铁结构环境的外来人员，导致人群容易慌乱中随意寻找出口，增加疏散的难度[1]。

当地铁火灾发生时，由于人群完全依靠事故照明和指示灯进行逃离，再加上浓烟影响，导致可视距离降低，人员疏散困难[2]。通过对100多年来国内外地铁典型事故死亡人数、发生频率的统计分析，发现地铁的重大事故主要集中在七大类[3]，其中地铁火灾事故占68%。为此，对地铁火灾的研究显得尤为重要。在地铁火灾中，烟气的高温、毒性和窒息是致人死亡的直接原因，对人员构成的威胁最大，且烟雾使能见度降低，不仅阻滞人员逃生，也加大了消防人员的救援工作难度。因此，对火灾发生时的烟雾浓度及其分布特性进行准确、有效的预测有利于帮助人群快速找到相对安全的逃生路线，降低火灾造成的人身安全损失[4]。在特定的能见度低、逃生出口不明确的情况下，为快速逃离火灾现场，本文在模拟地铁场景基础上，提出基于灰色马尔可夫预测模型的地铁场景最优路径规划算法。在存在多条逃生路径的情况下，根据路径上烟雾浓度、出口距离等其他因素进行实施规划，选择当前最优的路径帮助人群逃生[5]。对于地铁这样人流密集型公共场所，难于实地逃生演习，因此虚拟演练成为重要的逃生训练方式，本文将最优路径规划应用至虚拟逃生演练中，验证了本文方法的可行性及其应用价值。

1 相关工作

灰色系统是指部分信息已知、部分信息未知的系统，由邓聚龙教授在1982年提出。该理论通过灰色数据序列建立系统反应模型，并通过该模型预测系统可能的变化状态。其理论的实质是将无规律的原始数据进行累加生成，得到规律性较强的生成数列后再重新建模。由生成模型得到的数据再通过累加生成的逆运算累减生成得到还原模型，由还原模型作为预测模型[6]。该预测模型的优点是易于建立数学模型，需要的原始数据少，但对于波动性较大的数列拟合精度较差，预测精度较低，在火灾中不能满足实际预测的需要，所以必须提高其预测精度。马尔科夫链根据系统不同状态之间的转移概率来预测系统的发展趋势，它和系统当前的状态相关，与系统过去的状态无关，适用于预测波动性较大的数列。因此，马尔科夫链可以较好地弥补灰色系统理论在实际预测中的缺陷[7]。

将灰色系统理论和马尔科夫链结合在一起的预测模型——灰色马尔科夫预测模型，已经被广泛应用于瓦斯涌出量预测[8]、运动员长跑成绩预测[9]、物流量预测[10]、道路交通事故预测[11]、水果产量预测[12]等社会生活领域。在火灾事故方面，该预测模型多用于对火灾的发生次数和分布特性进行研究，通过把每年火灾事故发生的次数作为原始数据来对未来一段时间内火灾的发生次数进行预测，是一种预防性研究。毛占利等[13]通过对火灾发生次数进行回归分析，利用灰色马尔科夫预测模型进行预测研究；安春晖等[14]把火灾发生次数、直接经济损失、死亡伤亡人数作为原始数据，分别用灰色系统理论、马尔科夫链和灰色马尔科夫预测模型进行预测，得出灰色马尔科夫预测模型的精度明显高于前两种预测模型的结论。以上两种火灾事故相关研究均是对火灾发生次数的预测，对于已发生火灾的建筑并不适用，因此，为了减少已发生的火灾造成的人员伤亡与财产损失，本文从最优逃生路径规划方面对地铁火灾进行研究。

在火灾中，烟雾的毒性和窒息是致人死亡的直接原因。因此，对于发生火灾的地铁，利用灰色马尔科夫预测模型对可行的逃生路线进行预测十分重要，其预测结果能较好地指导人员快速确定逃生方向。本文采集每个时间段内烟雾的浓度作为原始数据序列，利用灰色马尔科夫预测模型对未来一段时间内烟雾的浓度进行预测，计算出烟雾浓度较低的方向，结合出口距离，为人群指出逃生路线，以期有效地降低人员伤亡率。

2 预测模型的建立

2.1 建立灰色GM(1,1)模型

将输入的烟雾浓度序列作为原始数据序列，建立灰色模型，计算出灰色预测值。

设原始数据序列为X(0)=(x(0)(1),x(0)(2),…,x(0)(n))，利用

(1)

求得X(1)的一次累加生成序列为X(1)=(x(1)(1),x(1)(2),…,x(1)(n))。

数列X(1)是1阶白化微分方程，记为GM(1,1)，即

(2)

其中：a为发展系数，反映所测数据序列的发展趋势；b为灰作用量，反映所测数据大小的变化关系。

z(1)是X(1)的紧邻均值序列

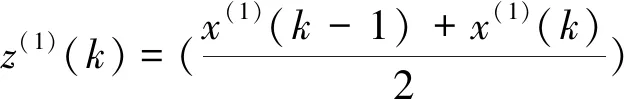
k=2,3,4,…,n

(3)

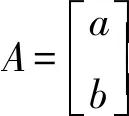
式(2)的解为

(4)

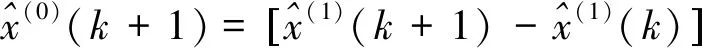
k=1,2,3,…,n

(5)

还原出X(0)的模拟值

2.2 状态划分

马尔科夫链是一种对事件发生概率进行预测的方法，该方法可以根据某些变量目前的状态来预测未来一段时间内系统可能出现的状态。状态的转移规律是马尔科夫链预测的关键，因此首先要对数据序列进行状态划分。在划分时，根据实际情况的不同，划分不同的状态。划分的状态越多，预测精度就会越高，但出现在每个状态内的数据个数也会相应减少。

本文对残差序列U(0)进行划分，

把非平稳随机序列U(0)划分为互不相交的状态，任一状态记为：

Ei=[⊗i-,⊗i+]i=1,2,3,…

其中⊗i-=uU(0)+v，⊗i+=uU(0)+v，u和v为常数。

2.3 建立转移概率矩阵

首先需要计算求得数据样本空间中由状态i经过k步转移到j状态的概率。

(6)

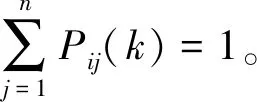
转移概率矩阵为：

(7)

在实际运用中，一般只考虑一步转移概率矩阵P(1)。

首先求出状态转移次数的矩阵

(8)

式中：Tij(1)为由状态Ei经一步转移到Ej的次数，初始值都为0。在T(1)中，若某一行中不都为0时，则分别用每个数除以每行的和就得到一次转移概率矩阵P(1)

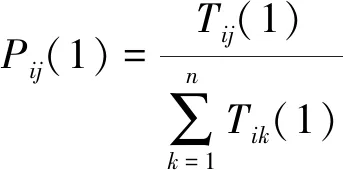
(9)

2.4 确定预测状态

状态序列为φ=(φ(1),φ(2),…,φ(n))，由某个状态φ(i)可以得到状态向量Qi，Qi初始化为(0,0,0,…,0)。

φi若为第x种状态，Qi中第x个分量的值就变为1。例如φ(i)处于第1种状态，则Qi=(1,0,0,…,0)。这样由状态序列就可以得到一个向量序列，记为Q=(Q1,Q2,,…,Qn)。由Q和转移概率矩阵P(1)计算预测状态E。E=QP(1)，E中的最大值对应的位置为预测状态E*。得到预测状态E*后,取其中间值作为要修正的值。用灰色预测值加上该修正值得到精度更高的预测值。

3 实验验证

为对算法的有效性进行验证，本文采用烟雾涌出浓度数据(见表1)概念。实验中用于输入的测试数据共121个，采样周期为1 h。在火灾事故中，由于烟雾扩散速度极快，采样周期要远小于1 h。此处采用这些数据是为了验证预测模型的精确度，且该预测模型只与原始数据相关，与采样周期无关。因此，可采用采样周期为1 h的浓度数据作为原始测试数据。

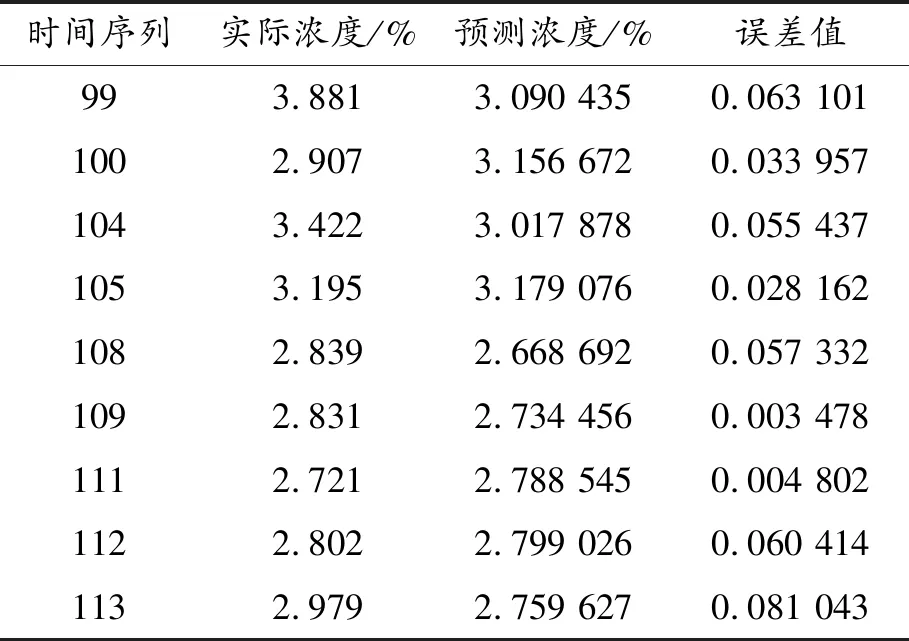
续表(表1)

图1为根据灰色马尔科夫模型预测的结果与实际数据的比较，预测值与实际值的拟合曲线非常接近，能较好地反映数据之间的波动性。灰色马尔科夫模型预测的误差分析结果显示，预测误差方差为0.489 661，平均误差为0.239 768，说明预测精度高、拟合度较好，可用于对实际烟雾浓度的预测。

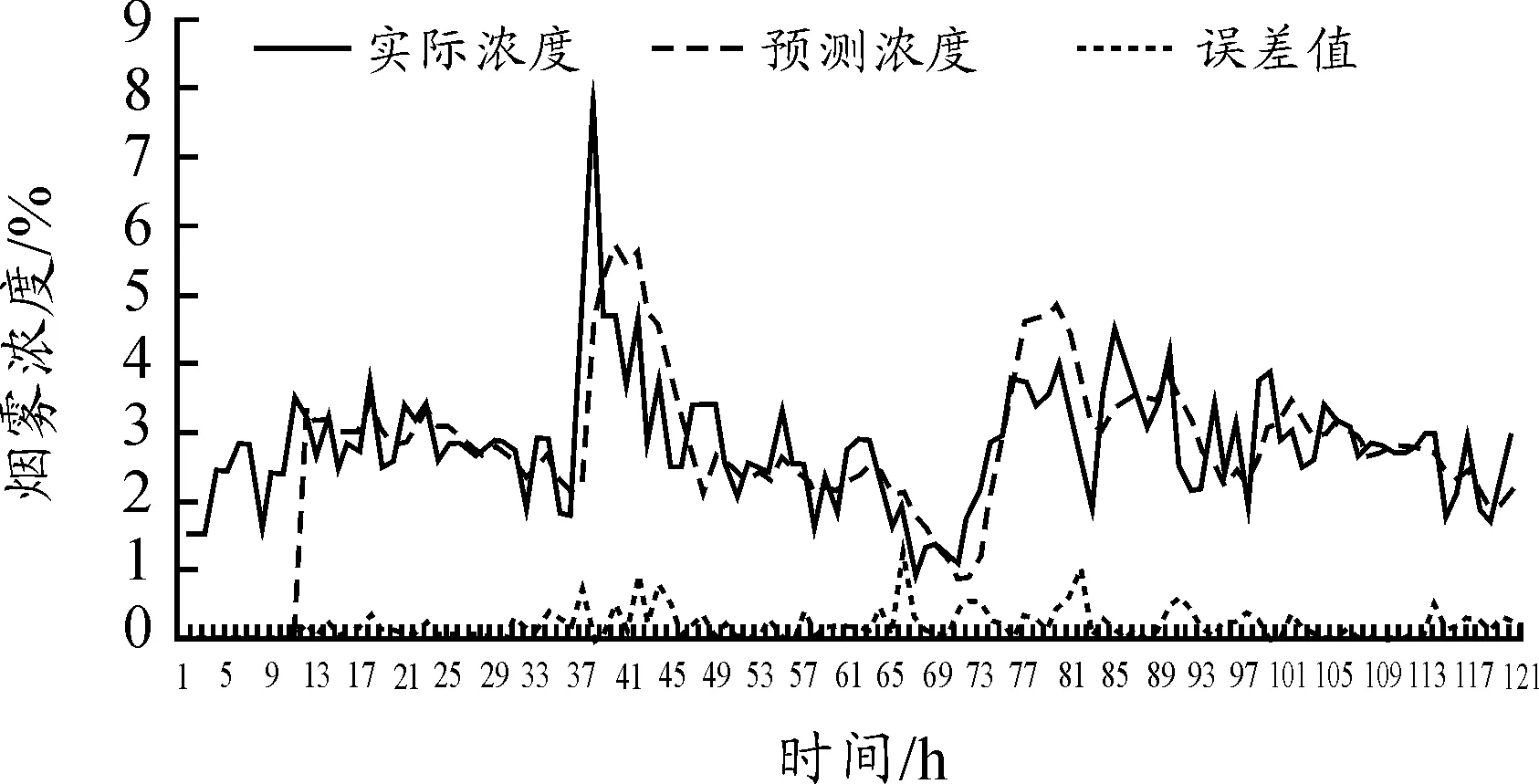
图1 预测浓度与实际浓度对比

4 仿真模拟

本文进行地铁站的建模与场景布局，采用3条通道逃生路径模拟火灾逃生。在每个逃生通道两边墙壁以及顶部设置烟雾浓度接收装置(如图2所示)进行实时烟雾浓度分析，根据烟雾浓度情况规划逃生路径。

图2 烟雾浓度接收装置

模拟系统画面小地图中有黄色带圈箭头指示标志，提示最终的逃生出口位置。该箭头规划的路径通过灰色马尔可夫预测模型进行计算，可根据当前角色位置信息、出口位置信息、路径上的烟雾浓度等信息，综合考虑可燃障碍物、火情大小等可量化的参数对未来一段时间内的影响，动态规划最优逃生路线，帮助训练对象快速逃离发生火灾的地铁站。

当地铁站内发生爆炸或火灾时，会产生大流量的烟雾，这时烟雾浓度传感接收装置开始工作，发出红色灯光，如图3所示。在接下来的时间段内，通过收集所有路径上的每一个烟雾浓度接收装置，用灰色马尔科夫模型预测烟雾浓度最小的逃生路径。烟雾的状态会随着时间的增加而越来越大，在整个过程中路径选择随着烟雾浓度的变化而相应地动态改变。在左上角的小地图中会给出逃生路径，小箭头指示方向即规划的逃生路线(如图3所示)。图3为烟雾浓度接收装置感知烟雾并发光，小地图中黄色箭头指示预测产生的逃生路径。

图3 烟雾浓度接收装置及预测路径

在用户完成模拟逃生训练之后，可对逃生系统训练所得分数进行评估。该评分结果是对用户进站到发生火灾直至最后逃生所做的详细用户行为记录。在训练系统中还设置了用户行为评分，用来记录模拟过程中出现的不恰当行为。系统会对这些不恰当行为做出记录并进行自动评分，为最终模拟逃生训练提供理论指导。模拟结束后给出反馈结果，如图4、5所示。

图4 行为评测失败结果

图4为模拟逃生训练的行为评测结果展示。在模拟过程结束后系统给出整体模拟训练的得分情况，例如对虚拟系统中所设工具使用情况的评分为5，对于训练过程中的其他不当行为如逃票、闯入地铁轨道等的评分和最后整体身体健康程度的评分。图5为模拟逃生训练的行为评测结果展示，如果能够在保证身体健康的情况下顺利完成训练，则系统会给出相应提示。

图5 行为评测成功结果

5 结束语

本文提出了基于灰色马尔科夫预测模型对火灾中的烟雾浓度预测并规划最优路径的算法，在火灾场景下利用灰色马尔科夫预测模型进行实时路径规划，帮助地铁人群快速逃生，并采用3D虚拟模拟实验对算法进行验证。实验结果表明该方法能较好地预估烟雾浓度，可使用该方法进行地铁火灾逃生模拟。

预测模型充分发挥了灰色系统理论和马尔科夫链的优势，既保留了数据的随机性，又体现了数据总体的发展趋势。通过灰色系统理论得到预测值，再通过马尔科夫链对残差序列进行状态划分，通过计算状态转移概率确定修正值，对灰色预测值进行修正，使结果更加准确。

在实际应用中，状态的划分受到诸多因素的影响，目前尚无统一的标准，所以该模型的实用性还需要进一步联系实际进行研究。对于火灾这种扩散速度极快的灾害，需要大量的烟雾数据来验证模型，因此，本实验还需要大量的原始数据作为支撑来进一步对模型进行精确度上的优化。