基于MFO-ELM的荷电状态软测量模型

蒋丽丽，陈国彬

(重庆工商大学融智学院， 重庆 401320)

电池荷电状态(state of charge,SOC)指电池在一定放电倍率下，剩余电量与相同条件下额定容量的比值[1]，100%表示全电池状态，0%表示空电池状态，是电池使用过程中的重要参数。SOC值可以让用户了解电池在需要充电之前还能继续工作的时间。近年来，电动汽车技术发展迅速，电池管理系统(battery management system,BMS)的一项重要研究内容是保证电池组的荷电状态(state of charge,SOC)在合理的范围内，防止过充电或过放电对电池造成损伤。因而，SOC的准确计算是BMS系统重要研究内容之一[2-3]。

SOC计算受电池工作状态、环境温度大小、电流大小等因素影响，并且随着充放电循环次数的增加，电池会发生不可逆的老化现象，因此SOC精确计算是一项困难任务[4]。设计精确的SOC指示系统的主要问题是电池和用户行为的不可预测性。SOC常见的计算方法有状态估计法，包括计量估计法、开路电压法、内阻法、卡尔曼滤波等[5-7]。这些方法已被广泛使用并在不同应用中获得了可接受的效果。然而，这些方法的缺点是由于计算复杂而需要更高的实现成本，且SOC的计算精度仍有待改善。

极限学习机(extreme learning machine,ELM)是一种新的前馈神经网络。与传统的单隐层前馈神经网络(FNN)相比，ELM由于具有分类精度高、泛化能力强、可调参数少等显著优点而得到较大发展[8-9]。ELM具有非线性的基本特性，对于外部激励能给出相应输出，针对电池高度非线性系统[10]，ELM能够建立准确的充放电模型。为了提升SOC预测精度，采用具有全局优化性能的飞蛾火焰优化算法(moth-flame optimization,MFO)[11-12]优化ELM模型参数。通过对电池电压、电流和温度数据进行训练学习，得到最优的MFO-ELM模型。最后，对某型号电池进行仿真实验，SOC预测结果表明了MFO-ELM算法的有效性。

1 飞蛾火焰算法

受自然界飞蛾导航启发，Mirjalili S在2015年提出飞蛾火焰算法(MFO)[11]。MFO以飞蛾行为为基础，通过一种特殊的称作横向定向导航的机制实现了勘探与开发的较好平衡，以获得全局优化性能。

在MFO算法中，飞蛾个体为优化问题的候选解，假设有n个飞蛾X=[x1,x2,…,xn]T,i=1,2,…,n，第i个飞蛾定义为xi=[xi,1,xi,2,…,xi,d]T，其中d为优化问题维数。火焰为当前迭代所获得的最佳位置，第i个火焰定义为fi=[fi,1,fi,2,…,fi,d]T。MFO算法捕焰行为和弃焰行为描述如下：

1) 捕焰行为。自然界中具有趋光特性的飞蛾Mi会朝着距离自身最近的亮光(火焰)Fj移动，其对数螺线捕焰轨迹数学模型为

S(Mi,Fj)=Di·ebt·cos(2πt)+Fj

(1)

式中:S(Mi,Fj)为更新后的飞蛾位置；b为与螺线形状相关的常量；t为[-1,1]区间的随机数；Di=|Fj-Mi|为飞蛾Mi到火焰Fj的距离。人工模拟的飞蛾捕焰轨迹如图1所示。

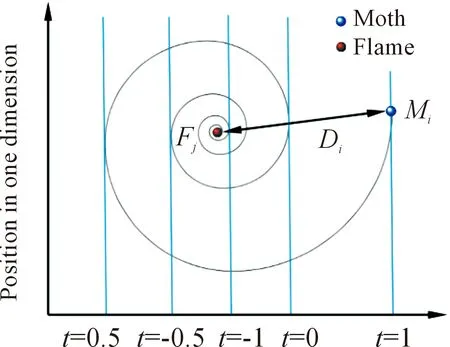
图1 飞蛾捕焰运动轨迹

图1描述了飞蛾Mi沿着螺线运动到火焰Fj以搜索全局最优解。MFO整个螺旋搜索过程以飞蛾的初始位置为起点，最优解位置为终点。

2) 弃焰行为：火焰数量通过弃焰操作逐渐减小，弃焰操作描述为

(2)

式中:t和T分别为当前和最大迭代次数；N为最大火焰数量。

2 极限学习机优化模型

2.1 极限学习机

极限学习机(extreme learning machine,ELM)是由黄广斌提出的求解单隐层神经网络的算法。ELM最大的特点是对于传统的神经网络，尤其是单隐层前馈神经网络(SLFNs)，在保证学习精度的前提下比传统的学习算法速度更快。

ELM是一种新型的快速学习算法，对于单隐层神经网络，ELM 可以随机初始化输入权重和偏置并得到相应的输出权重。设n、L、m分别为网络输入层、隐层和输出层的节点数，其基本结构如图2所示。

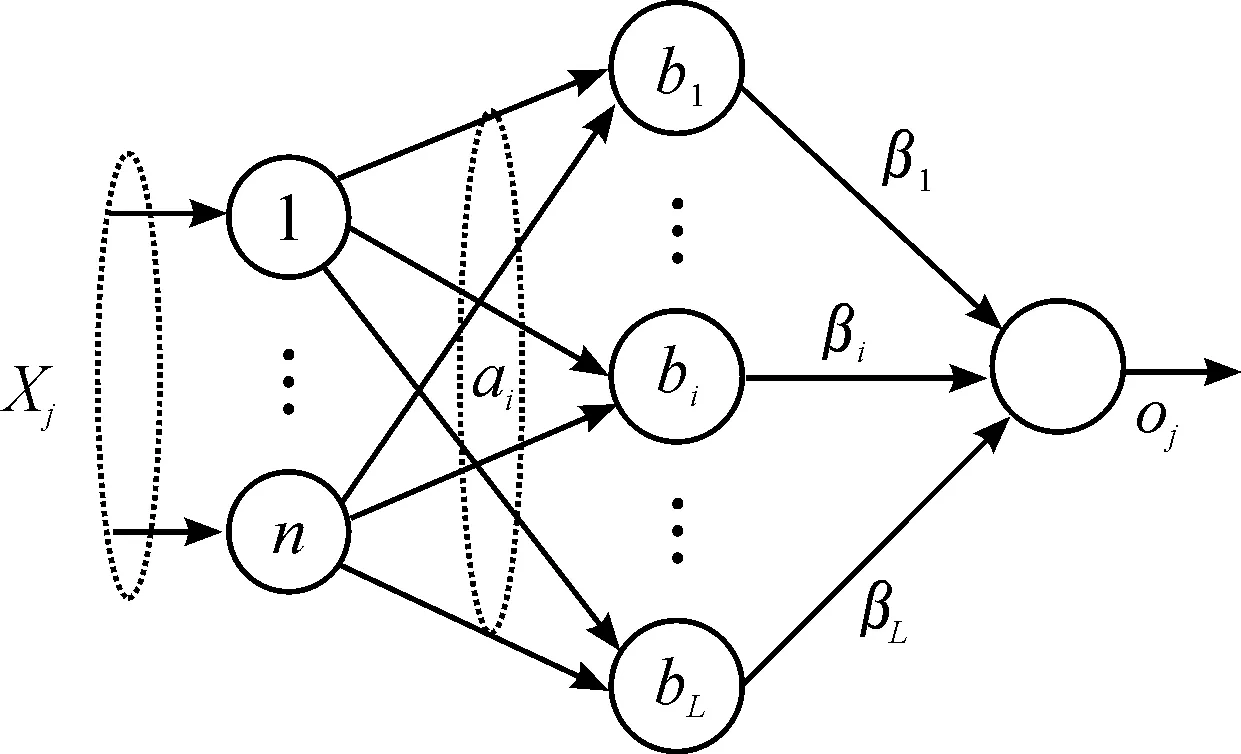
图2 ELM基本结构

图2中：输入层n个节点表示样本维度；Xj表示第j个样本；隐含层有L个节点，L越大，表达能力越强，节点i与输入层连接权值为ai，与输出层连接权值为βi；输出层oj表示样本j的输出。假设有任意的样本(Xj,Tj)，其中输入样本为Xj=[xj1,xj2,…,xjn]T∈Rn，输出向量为Tj=[t1,t2,…,tm]T∈Rm，则单隐层神经网络可表示为

(3)

式中：g(X)为隐层神经元的激活函数；ai=[ai,1,ai,2,…,ai,n]T为输入权重；βi为输出权重；bi是第i个隐层单元的偏置。

ELM学习的目标是使输出的误差最小：

(4)

式中：S=(ωi,bi,i=1,2,…,M)，包含了网络输入权值及隐层节点阈值；β为输出权值矩阵。

ELM的训练目标是寻求最优的S,β。min(E(S,β))可进一步描述为

minE=min||H(ω,b,X)β-T||

(5)

其中：H是隐层节点的输出；β为输出权重；T为期望输出。

H(a1,…,aL,b1,…,bL,X1,…,XL)=

(6)

(7)

(8)

这等价于最小化损失函数

(9)

传统的基于梯度下降法的算法在迭代过程中将调整所有参数，而在ELM算法中，一旦输入权重ai和隐层的偏置bi被随机确定，隐层的输出矩阵H就被唯一确定。训练单隐层神经网络可以转化为求解一个线性系统Hβ=T，且输出权重可以被确定：

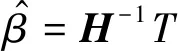
(10)

2.2 ELM优化模型

为了提升ELM预测精度和泛化能力，采用具有全局优化能力的MFO算法进行模型参数的优化选择，并得到最优的SOC模型，即MFO-ELM模型。模型参数调整示意图如图3所示，其核心思想是将SOC样本数据作为ELM的输入，得到网络的一组输出，将输出值与实验值作对比，得到预测误差。MFO算法根据预测误差调整整个网络的模型参数，直到误差降到允许误差为止，并得到最终的SOC预测模型。

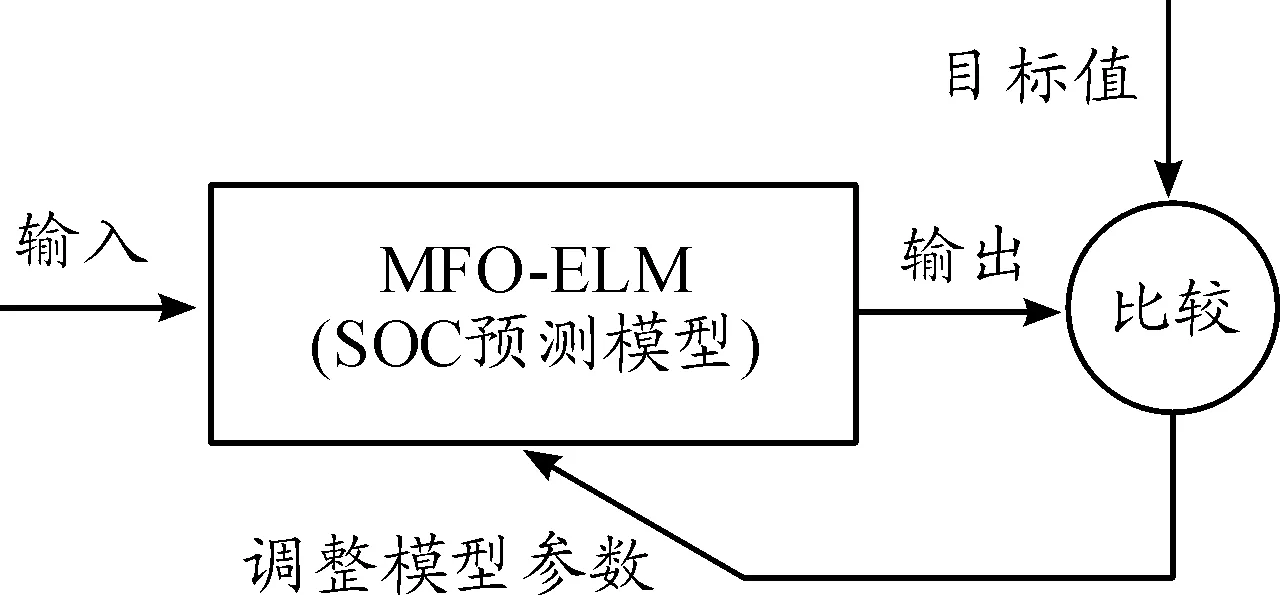
图3 ELM模型参数调整示意图

MFO算法优化调整ELM模型参数的适应度函数J定义如下：

(11)

3 SOC预测实例

3.1 预测步骤

铅蓄电池工作过程中，SOC随着电池电压、电流、温度、极化电阻的变化呈现复杂非线性关系，因而，选择输入变量为电池电压、电流、温度和极化电阻，输出变量为SOC值。通过对MFO-ELM进行训练，得到最优的MFO-ELM模型对未来SOC样本进行预测，SOC具体实现步骤如下：

1) 对采样数据进行相关性分析和预处理，构成训练集和测试集。

2) 确定ELM的SOC模型所需的运行参数，确定MFO算法各项参数，建立ELM预测模型。

3) 用训练集对ELM网络进行训练，MFO算法不断调整网络参数，到达终止条件时为止，获得MFO-ELM的SOC预测模型。

4) 将测试集送入到训练好的MFO-ELM模型进行泛化能力测试。将得到的预测值与真实值进行对比，计算误差。若误差较大，表明模型泛化能力不足，则需重新采集大量数据进行SOC预测模型的训练。

3.2 数据采集

铅蓄电池常见的充放电倍率为0.1～1 C，通过蓄电池测试分析仪对某型号的铅蓄电池按照0.1、0.2、0.33、0.75 C的充放电倍率进行测试，测试结果如表1所示。表1中前25组数据用来训练模型，后5组用来验证模型。

表1 SOC预测样本

3.3 仿真结果

取25组放电倍率为0.1、0.2、0.33、0.75 C的数据作为训练样本，用MOF优化的ELM模型对训练样本进行训练。针对训练样本，SOC预测结果及SOC预测相对误差如图4、5所示。从图4可以看出，针对训练样本，MFO-ELM预测结果几乎与SOC真实值完成重合。图5显示MFO-ELM预测相对误差较小，最大相对误差为2%，满足工程需求。

图4 MFO-ELM模型的SOC预测结果

为了验证模型的泛化性能，采用后5组测试样本进行仿真实验。图6、7为MFO-ELM与ELM模型预测结果及预测相对误差。

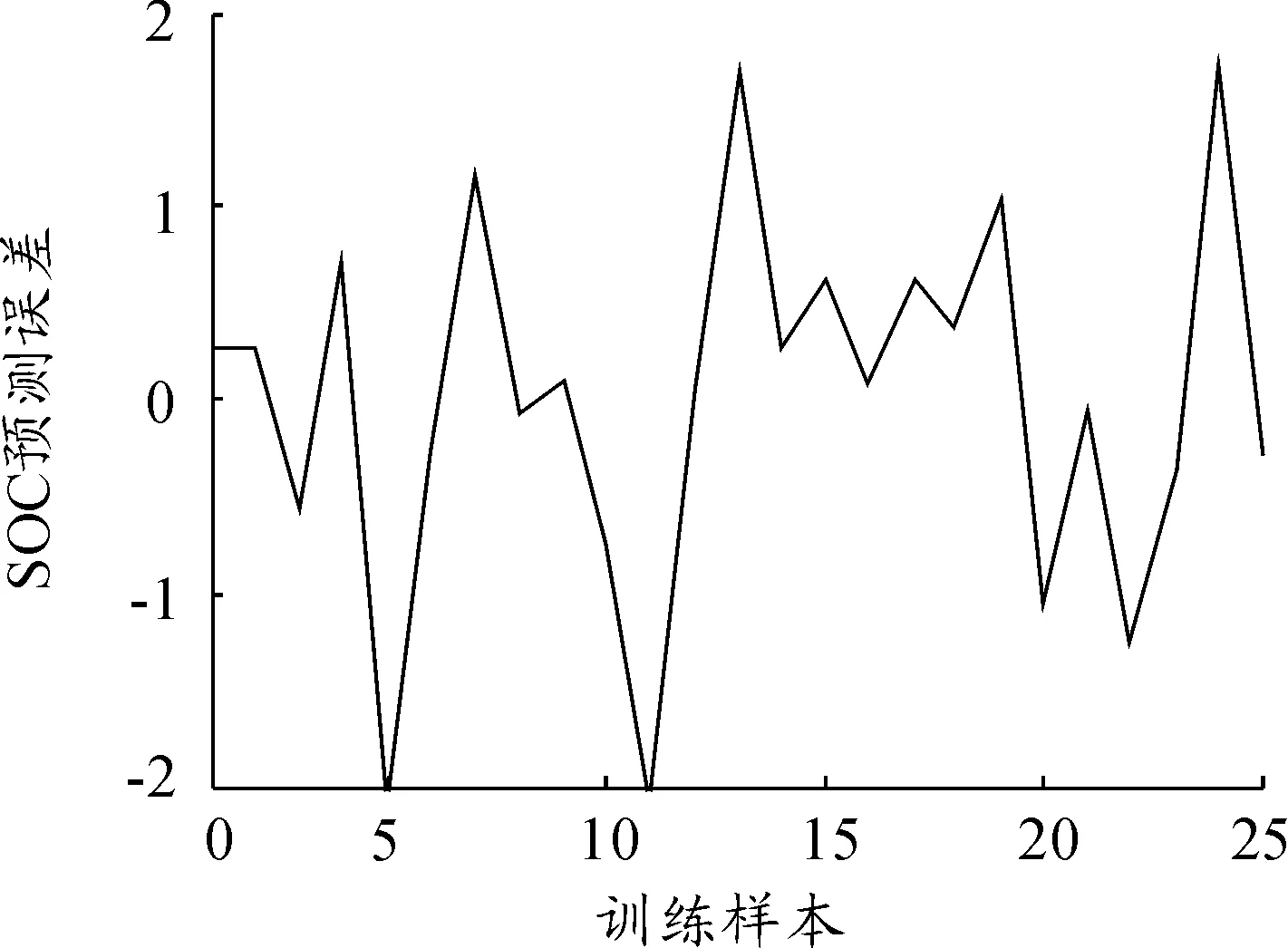
图5 MFO-ELM模型的SOC预测误差

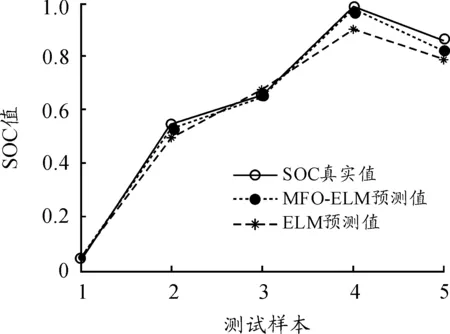
图6 SOC预测结果

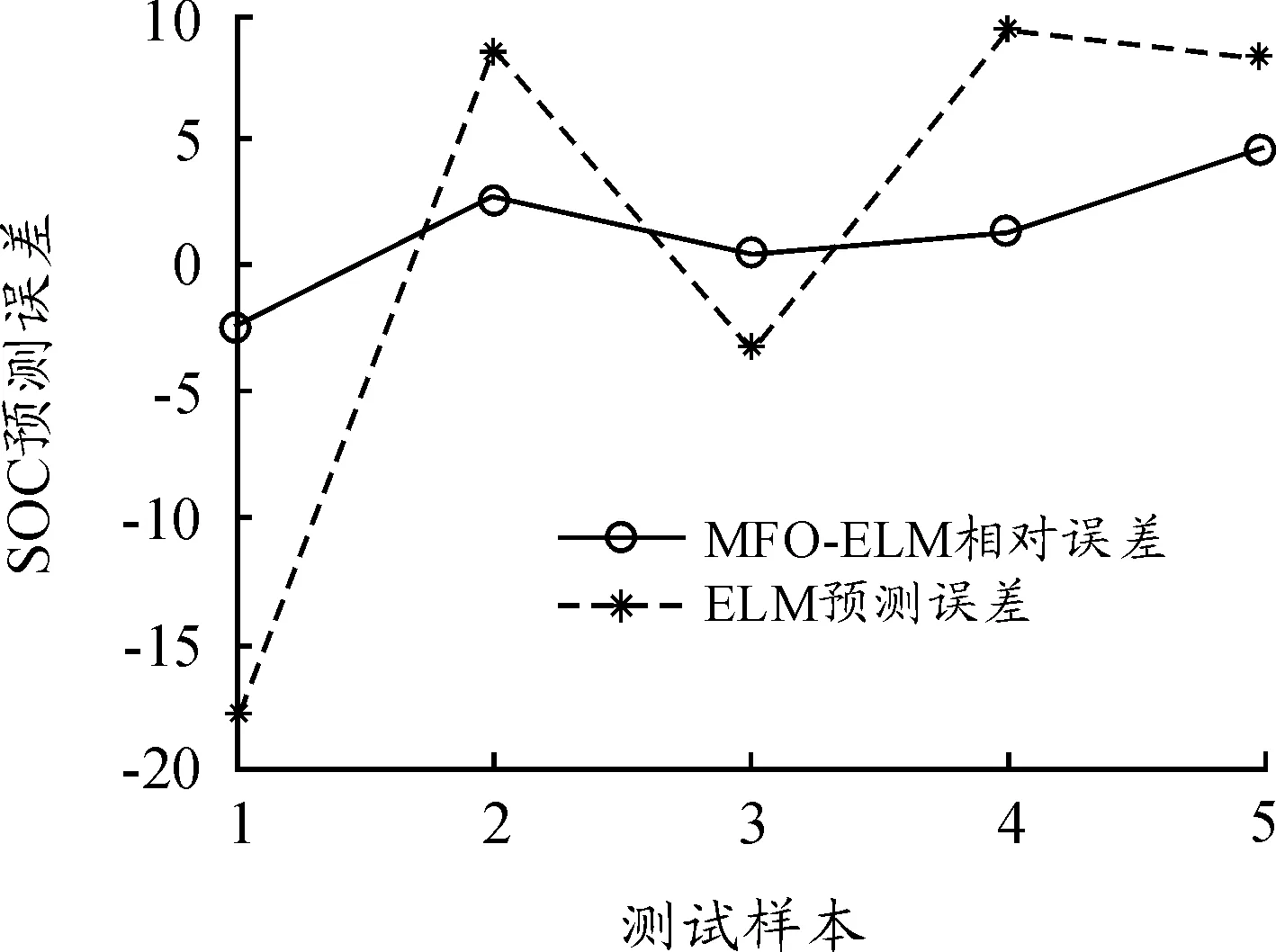
图7 SOC预测误差

由图6可以看出，MFO-ELM模型与ELM模型的SOC预测趋势一致，但采用MFO算法优化的ELM模型预测结果与真实值明显更加吻合，尤其是针对样本2、4、5，MFO-ELM模型比ELM模型预测效果更好，总体上，MFO-ELM模型的预测精度更好。从图6预测相对误差曲线可以看出：MFO-ELM模型的预测相对误差低于5%，而未经优化的标准ELM模型预测相对误差超过15%；同时，MFO-ELM模型的预测误差曲线相对较小且平缓，表明MFO-ELM泛化能力更强。总之，MFO算法能够改善ELM模型的预测精度，MFO-ELM模型的SOC预测相对误差低于5%，满足实际需求，仿真实验验证了MFO-ELM模型的有效性。

4 结束语

电池准确的SOC值对于方便用户和延长电池寿命非常重要。针对SOC值难以精准预测的不足，利用ELM非线性处理特性，从电池充电、放电测试周期中提取模型参数，通过电压、电流、温度和极化内阻数据作为输入变量，建立了SOC预测模型，避免电池内部复杂的非线性关系和数学解析过程。在ELM模型训练过程中，采用MFO算法优化选择ELM模型参数以提升SOC预测模型的泛化能力。基于ELM的SOC预测模型可以在基于低成本微控制器的BMS系统上运行，以实现SOC预测功能。最后通过仿真实验测试MFO-ELM模型的预测性能，模型预测误差控制在5%以内，满足工程需求，可为电池的状态监测、维护、安全可靠运行提供准确的SOC值。