基于复合评价值的小波去噪参数选定方法
焦志浩,吕迎春
(太原理工大学 电气与动力工程学院, 太原 030024)
在处理非稳态噪声信号时,考虑到小波变换相比于傅里叶变换在时域和频域具有更好的刻画能力和其本身的多分辨性的原因,小波变换成为了近几年降噪领域的研究热点。 含噪信号的小波阈值去噪,主要研究集中在小波基函数的选取与构造、分层数确定和阈值函数的改进[1-2]。对小波阈值函数的研究主要集中在提出或改进硬阈值函数、软阈值函数、硬软阈值折中和自适应阈值函数等方面[3-5]。对于小波基和分层数的研究,结合噪声特征值提取算法、香农熵定理、分解系数比等方法,实现对小波基或者分层数的自适应选择[6-9]。
以上研究都是从单一的某个方面选定小波去噪参数,无法一次性通过一种方法对小波去噪参数进行选定,这就导致在使用小波阈值去噪时,只能逐项选定某一项参数,致使选取过程过于零散,无法形成统一的选取过程。本文尝试将小波基函数和分层数的选取统一到同一方法中,在确定某一个参数之后,再确定另一参数,使得参数的选择过程简化。因此,本文提出了一种基于复合评价值的小波去噪参数选择方法,通过构建复合评价值来统一确定小波阈值去噪法中小波基和分层数。
1 优选评价指标构建复合评价值
1.1 小波去噪质量评价指标
传统的评价指标一般包括均方根误差(RMSE)、信噪比(SNR)、平滑度(r)。一般而言,均方根误差(RMSE)是指去噪后信号与原信号的均方误差,体现了信号的细节去噪情况,均方根误差越小,表示去噪效果越好。信噪比(SNR)是指原始信号能量与噪声能量的比值,体现了噪声信号对于整体信息的影响,信噪比越高,去噪效果越好。平滑度(r)是指去噪后信号1阶差分的方差根与原始信号1阶差分的方差根之比,体现了信号的整体变异信息,平滑度越小,表明去噪效果越好。
1.2 构建复合评价值
信号在小波变换以后产生细节信息和逼近信息,细节信息代表信号的细节分量,逼近信息代表信号的整体特征。由于小波阈值去噪中,阈值处理主要是针对细节信息,可以选取均方根误差作为评价指标。同时,平滑度作为衡量信号整体变异信息的指标,可以代表逼近信息的指标。因此,从信号进行小波分解后的细节信息和逼近信息的角度,选取均方根误差和平滑度2个评价指标,来衡量小波阈值去噪效果。
根据朱建军等[10]的融合方法,首先对均方根误差和平滑度进行归一化,再利用变异系数法[11]确定2个指标的权重,最后,将权重值与评价指标值线性组合,得到复合评价值。变异系数法是利用评价体系中的既有信息计算各指标的权重,反映被评价指标之间的差距,是一种客观赋权的方法。在本文中,均方根误差和平滑度作为2种不同性质的信息,在指标融合的过程中,需要分别确定其在复合评价指标中的权重。系数变异法作为一种客观反映不同指标差距的方法,可以用来确定均方根误差和平滑度在复合评价中的权重。通过计算均方根误差和平滑度的标准差与均值的比,得到变异系数,再求取各变异系数在整体中的比值,即可得到两者的权值,具体定权过程由式(1)~(4)所示。
由于2个指标融合以后,随着分解层数的增加,势必会出现一个极值[10],而极值点代表细节信息和逼近信息的最佳重构点,也就是信号去噪效果的最优点,同时由于均方根误差和平滑度的值越小去噪效果越好,因此,可以得出复合评价值越小,去噪效果越好。
融合的具体过程如下:
(1)
(2)
(3)
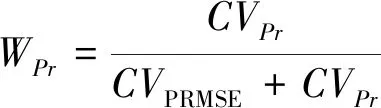
(4)
T=WPRMSE×PRMSE+WPr×Pr
(5)
式中:PRMSE和Pr表示均方根误差和平滑度的归一化值;CVPRMSE和CVPr表示均方根误差和平滑度的变异系数;σPRMSE和σPr表示均方根误差和平滑度的标准差;μPRMSE和μPr表示均方根误差和平滑度的均值;WPRMSE和WPr表示均方根误差和平滑度变异系数的权值;T表示复合评价指标值。
2 小波阈值法去噪
2.1 小波阈值去噪的基本原理
小波阈值去噪的基本原理是信号通过小波变换以后分成细节信息和逼近信息2个部分,然后根据设置的不同阈值函数,将关联的小波系数给予保留或者按照某种规律进行收缩,最后利用小波逆变换将处理后的信号进行重构。
噪声信号的数学模型可以使用加性噪声信号来表示,其原理是在纯净信号中加上等信号长度的高斯噪声信息。其公式如下:
f(t)=v(t)+n(t)
(6)
式中:f(t)是含噪信号;v(t)是纯净信号;n(t)为服从正态分布且方差为0的高斯噪声信息。
去噪过程的数学公式描述如下:
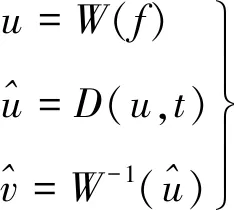
(7)

在这个过程中,第1步选择合适的小波基和分层数;第2步选择合适的阈值函数和确定最佳阈值进行去噪;第3步利用小波逆变换,将处理以后的信号重构。
2.2 小波参数的选取
2.2.1小波基和分层数的初选
小波基函数决定了信号分解的描述类型,一般对于不同的信号采用的小波基函数也有所不同,为了使超声含噪信号的去噪效果达到最优,尽可能在信号分解以后产生较多的小波系数。本文选用Symlet小波,Symlet小波是由Daubechies小波系改进而来,具有良好的正则性和对称性,在小波重构时可以使重构信号具有更好的光滑性。
在小波阈值去噪法中分层数的选择决定了信号分解的完整性,若分解层数过低,会导致原始信号与噪声信号的匹配特征不明显,若分解层数过大,重构后的信号失真性变大。因此,本文对于分层数的选取,借助经验法[12]先选取分层数的大致范围,同时为增加实验的严谨性,选取了2~9层。
2.2.2小波阈值函数的选取
小波阈值去噪中最重要的环节是小波阈值函数的选取。在小波阈值去噪中,硬阈值(H)去噪方式具有最大保留高频系数的特点,软阈值(S)去噪方式具有保持信号的连续性的特点,可以使得去噪信号重构以后更加光滑。硬软阈值是应用最早、最简洁和最成熟的2种去噪方式,其他的阈值去噪方式大都是在其基础上改进而来,去噪结果也都是对比软硬阈值去噪方式的结果。本文重点在于构建符合评价值选取小波基和分层数,使用硬软阈值去噪方式的意义在于增加实验结果的可信性和可靠性,以此来与其他文献做对比。因此,本文采用硬阈值(H)和软阈值(S)二种方式来分别处理不同的含噪信号。
硬阈值和软阈值函数表达式为:
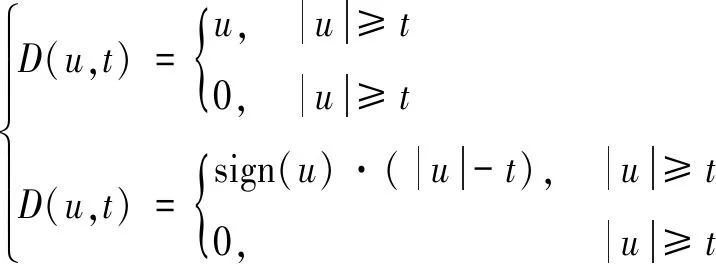
(8)
式(8)中,上式为硬阈值函数,下式为软阈值函数。硬阈值函数是指:小波系数的绝对值小于阈值时,小波系数置零;反之,保留原系数。软阈值函数是指:小波系数的绝对值大于阈值时,将小波系数的绝对值与阈值做差;反之,小波系数置零。
阈值选择的方法是采用基于史坦无偏似然估计(二次方差)原理的自适应阈值选择。对于给定的一个阈值t,得到其似然估计,再将似然t最小化,就得到所选的阈值t。
3 参数统一选定方法设计及实验结果分析
本文利用Matlab 2014b仿真平台,采用自带的通用blocks和bumps信号,超声回波信号采用理想状况下的双指数模型[13],模拟频率为40 kHz,采样频率为1 000 kHz的T/R40系列的信号模型。
3.1 参数统一选定方法步骤
1) 初选小波参数。大致确定小波基的类型和分层数的范围。
2) 小波阈值法去噪。使用硬软阈值2种去噪方式,对含噪信号进行去噪。
3) 融合评价指标得到复合评价指标值。去噪以后得到均方根误差和平滑度指标,融合得到复合评价值。
4) 确定分层数和小波基。根据得到的复合评价值,首先确定分层数,进而确定小波基。
3.2 实验结果分析
理想状态下的blocks、bumps信号如图1所示。为模拟噪声信息,在原始信号上加入10 dB的高斯白噪声,其含噪信号如图2所示。
图3和图4分别为blocks、bumps含噪信号在软硬阈值去噪方式下的复合评价值的变化趋势。分析可知,不同的小波基随着小波分解层数的不断增加,其复合评价值变化规律大致相同。小波变换分层数从2层到4层,复合评价值逐渐下降;从4层到9层,复合评价值逐渐增大。由此可见,复合评价值在4层取得极小值,根据复合评价值的意义,小波的最优分解层参数为4层。
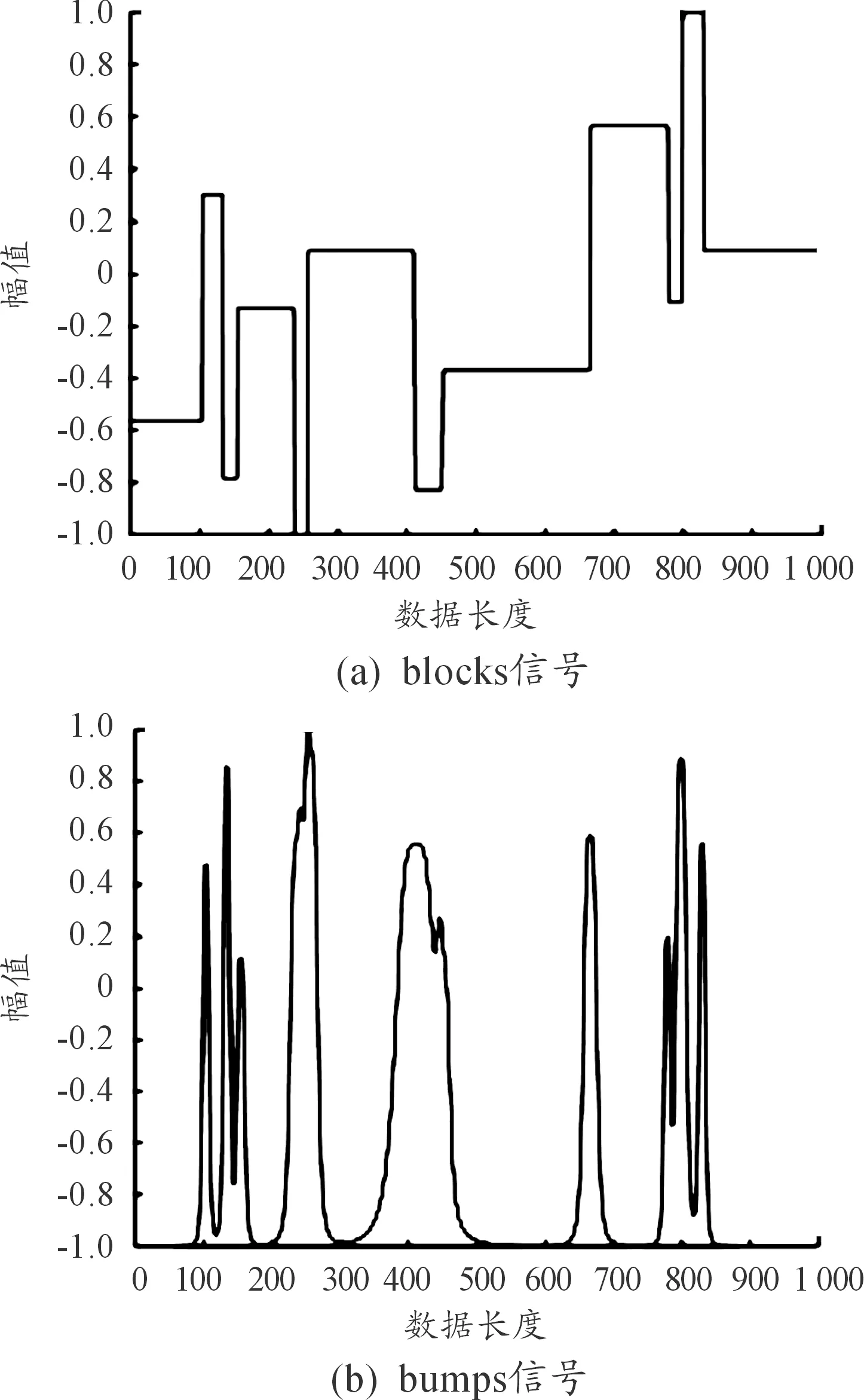
图1 原始信号
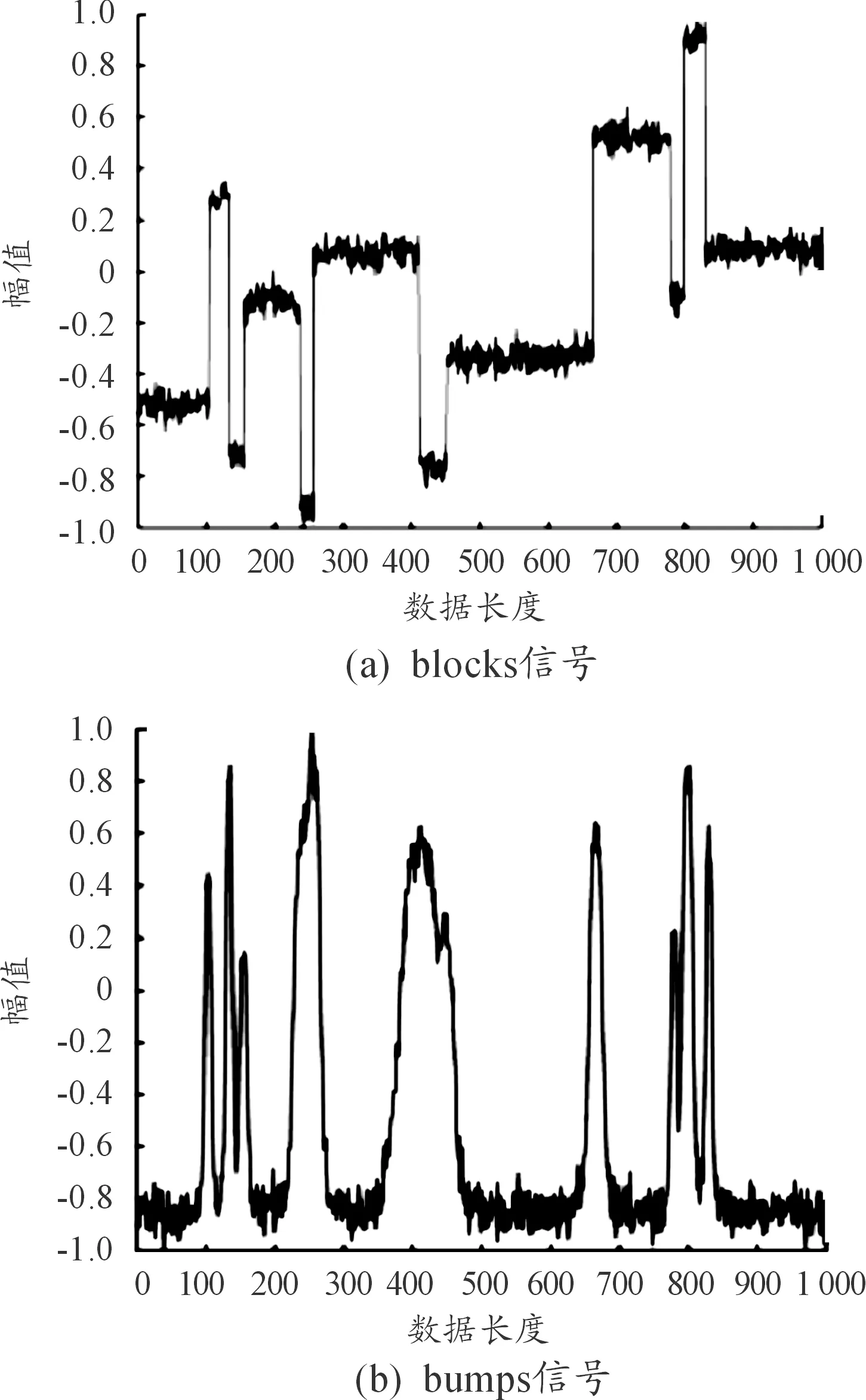
图2 含噪信号

图3 硬阈值(H)下不同信号的复合评价值变化趋势
表1和表2分别为4层分解数下blocks、bumps含噪信号在软硬阈值去噪方式下的复合评价值。分析可知,blocks含噪信号在选取sym7小波基时,复合评价值最小。根据复合评价值的意义,小波的最优小波基参数为sym7小波基;bumps含噪信号在选取sym6小波基时,复合评价值最小,根据复合评价值的意义,小波的最优小波基参数为sym6小波基。

表1 blocks信号复合评价值

表2 bumps信号复合评价值
由上述分析过程可知,对于blocks、bumps含噪信号使用小波阈值去噪方法,选择硬软阈值去噪方式。通过复合评价值的变化趋势和寻找最小值点,可以将小波阈值去噪参数中的小波基函数和分层数的选取统一到一个方法中。所以,bumps含噪信号使用小波阈值去噪方法,选用 sym7小波基函数,4层分层数,取得了最好的去噪效果;bumps含噪信号使用小波阈值去噪方法,选用 sym6小波基,4层分层数,取得了最好的去噪效果。表3为本文方法取得的去噪结果,从信噪比和均方根误差2个方面衡量了含噪信号的去噪效果。表4为文献[14]取得的去噪效果,也从信噪比和均方根误差2个方面衡量了去噪效果。将表3与表4相对比可知,本文方法的去噪效果优于文献[14]的去噪效果,证明本文方法中统一选择小波基和分层数的方法是合理且有效的。去噪效果图如图5和图6所示。
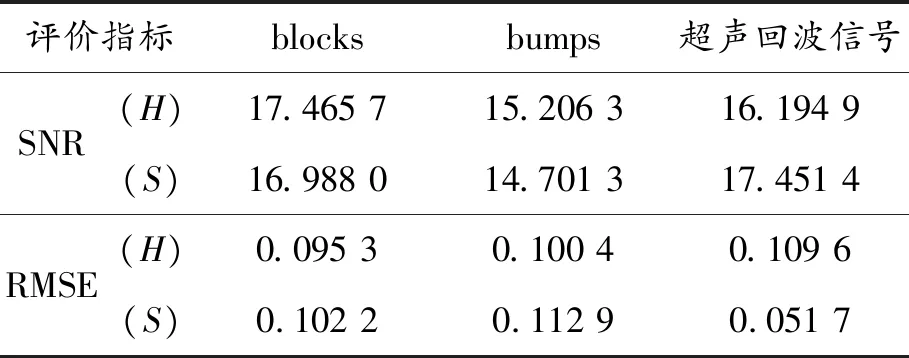
表3 本文方法去噪结果
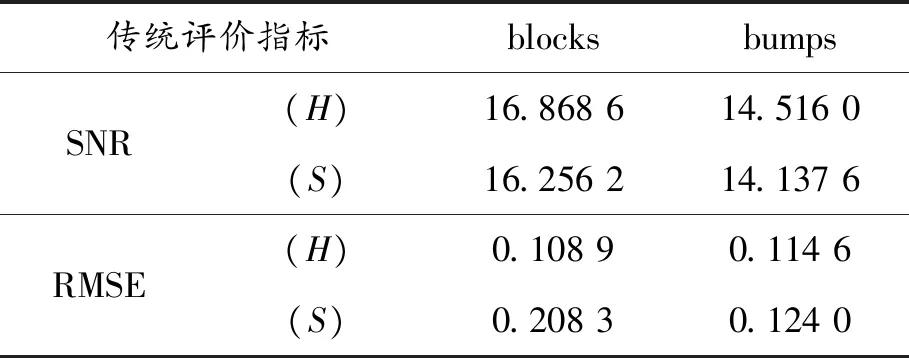
表4 文献[14]去噪结果
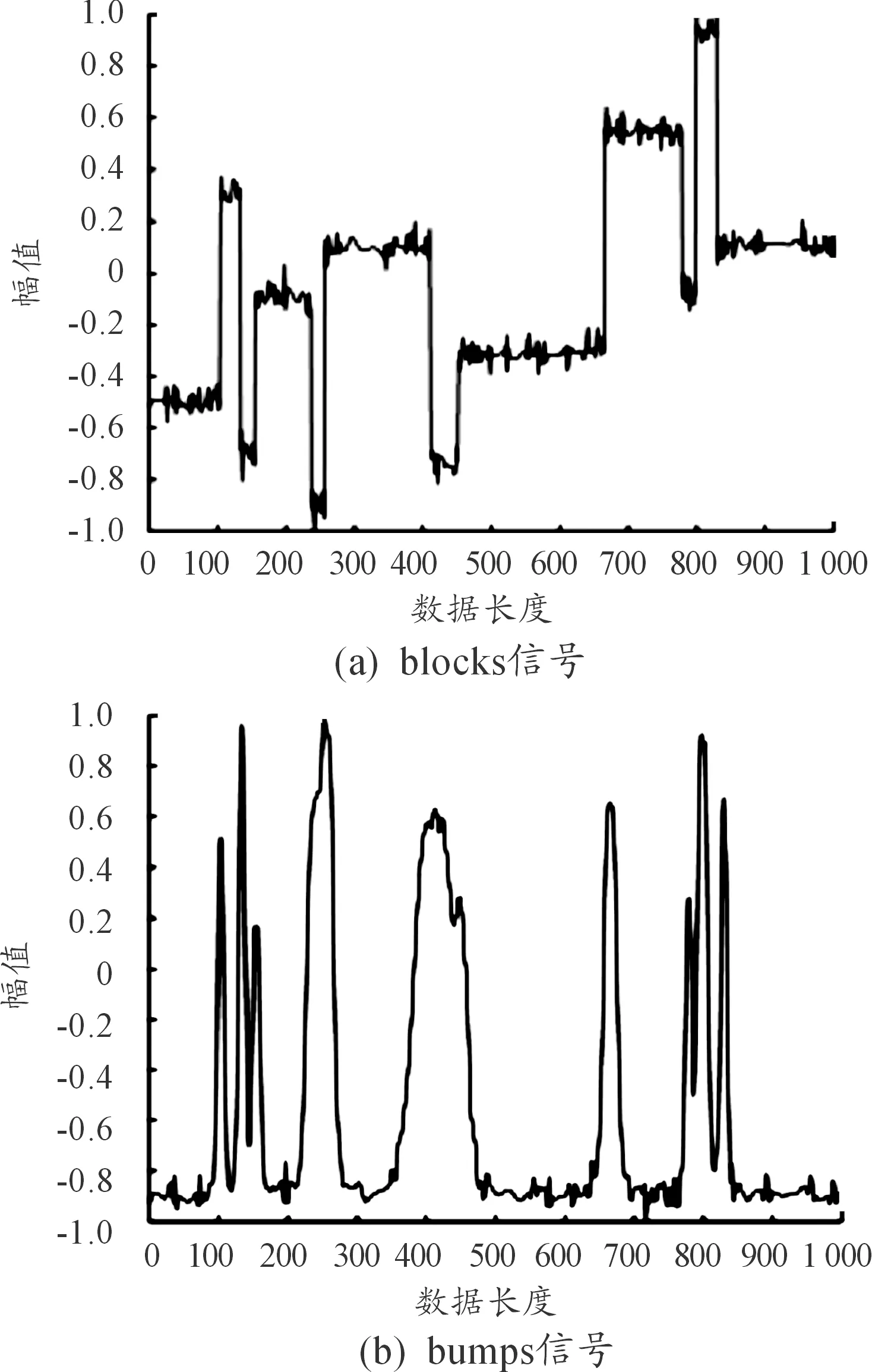
图5 硬阈值去噪效果
最后,将本文方法应用到超声回波信号小波阈值去噪中,超声回波信号和含噪如图7所示。通过复合评价值的变化趋势和寻找最小值点,确定了小波阈值去噪法选定参数为sym7小波基和4层分层数。去噪结果如表3所示,去噪的效果如图8所示。
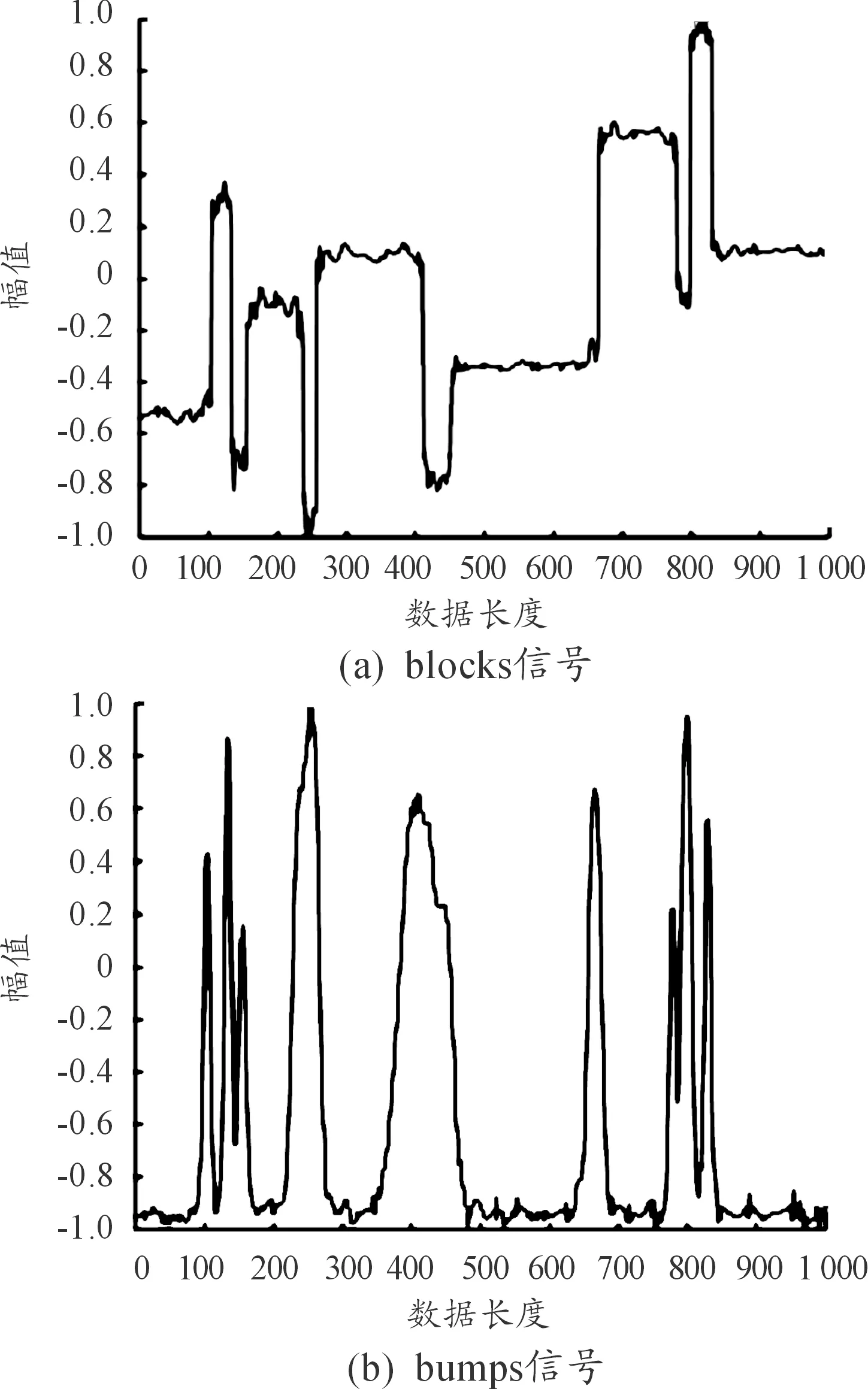
图6 软阈值去噪效果
4 结论
为了解决含噪信号在使用小波阈值去噪时的小波基和分层数的难以统一选定问题,将小波变换对信号分解的意义与传统评价指标的意义相结合,融合得到复合评价值。在小波阈值去噪以后复合评价值的变化趋势和极值点统一确定小波基和分层数,且将方法应用到超声回波信号去噪中。本文可以归纳出以下结论:
1) 小波去噪质量评价指标均方根误差和平滑度融合得到的复合评价值,其总体变化趋势呈现先下降后上升,出现的极值点可作为选取小波阈值去噪参数的依据。
2) 存在极值点以后的复合评价值并不是都符合增大的趋势。
3) 下一步工作在本文方法的基础上,结合自适应阈值函数,研究如何达到更优的去噪效果。
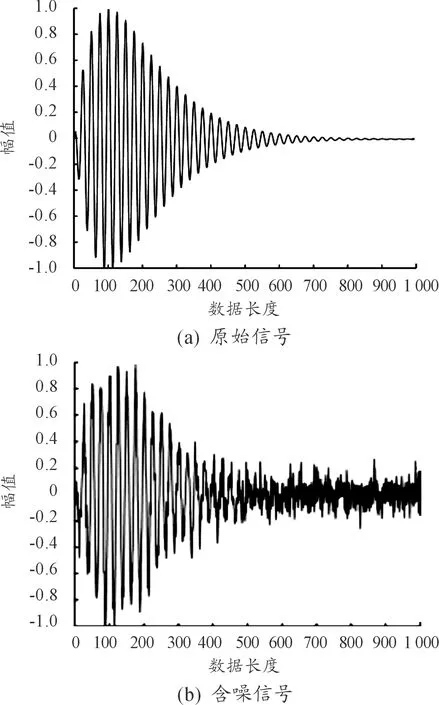
图7 超声波信号

图8 不同阈值下的去噪效果

