基于分形理论的齿轮结合面法向接触刚度研究
赵林林,黄小平,周忠旺
(1.南京林业大学 机械电子工程学院, 南京 210037;2.江苏财经职业技术学院 机械电子与信息工程学院, 江苏 淮安 223003)
机械结合面参数会影响整机设备的性能,而齿轮接触是最常见的一种接触,广泛应用于大型机械中,因此研究齿轮接触性能将有利于提高大型机械设备的加工性能。
齿轮的啮合面属于运动结合面,当受到动载荷时,齿轮结合面间会产生微小的相对位移或角位移,使得结合面间既存储能量,又消耗能量,表现出既有弹性又有阻尼,即存在接触刚度和接触阻尼,这种动态特性将对齿轮轮齿的动态特性产生很大的影响[1]。
虽然可以采用有限元法来实现齿轮的动态特性的仿真,其接触单元为齿轮结合面的计算提供了一种方法,但是刚度、阻尼等物理参数的确定对结合面来说很困难,造成了结合面的精确计算是齿轮性能预估的瓶颈。
齿轮结合面的切向接触刚度是机械结构整体刚度的重要组成部分,甚至称为整体刚度的薄弱环节,因此需要对齿轮结合面的接触刚度进行研究,而齿轮结合面的接触刚度包含法向接触刚度和切向接触刚度。本课题组在文献[2]中,已对齿轮结合面的接触刚度进行过分析研究,本文重点对齿轮结合面的法向接触刚度进行研究。
以前齿轮结合面的法向接触模型[3-5]相对简单,本文则考虑了域扩展因子Ψ的影响,并引入了微接触截面积a′,研究齿轮的齿面形貌对齿轮法向接触刚度的影响。
1 齿轮粗糙表面的分形模拟
齿轮的接触表面大多数是通过各种机加工的方法来实现的,机加工的表面质量对齿轮结合面的接触行为影响很大。文献[6]给出了45碳钢不同加工精度的磨削表面轮廓曲线。
利用W-M函数可以描述各向同性均匀粗糙表面[7-8],其表达式为:
(1
(1)
式中:D为分形维数,G为表面特征长度尺度参数,γn决定表面粗糙度的频谱。其中,最低频率与取样长度有关,即γn=1/L,L为取样长度,γ=1.5,能够适应高频谱密度和相位的随机性[6,8]。在模拟齿轮粗糙表面时,利用Matlab软件实现,n的取值为1~100。x为采样长度(mm),z(x)为轮廓高度(μm)。
2 齿轮粗糙表面微接触点大小分布函数
Wang等[9]引入了微接触截面积a′,并考虑了域扩展因子Ψ,得到粗糙表面的接触点的大小分布函数,此分布函数假设为一个粗糙表面和一个光滑平面的接触,而齿轮啮合是曲面与曲面的接触,因此引入表面接触系数λ[3],构造齿轮粗糙表面微接触点的大小分布函数为
(2)
式中λ为表面接触系数,
λ=λ0P′C2x
其中λ0为两啮合齿轮初始接触时的表面接触系数,
P′为两曲面间的法向载荷;x为综合曲率系数,
E为综合弹性模量;B为两齿轮啮合时的有效接触长度;R1、R2为两齿轮在接触齿廓处的曲率半径无侧隙安装时即为分度圆半径,+为外啮合,-为内啮合,C2为常数,C2=0.5,Ψ为微接触大小分布的域扩展因子,与分形维数有关,满足下列超越方程,其物理意义和取值可查阅文献[6],

Ar为结合面的真实接触面积[10-11]。

图1 齿轮副接触模型[10,12]
3 齿轮结合面法向载荷与真实接触面积的关系
在计算齿面接触强度时,仅考虑在节点处啮合。根据文献[5]中提出的齿轮表面接触系数来分析齿轮结合面的接触问题。
(3)
式中:Pc为相互啮合的两齿轮的法向载荷;P为两粗糙平面相互接触时的法向载荷。
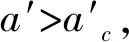
(4)
(D=1.5)
(5)
式中H为较软材料的硬度,
k=H/σy
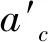
分别对式(4)(5)进行量纲为一化,得到:
(6)

(7)
(8)
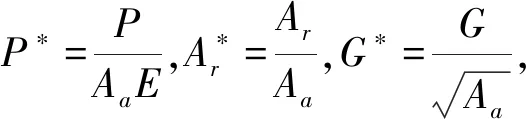
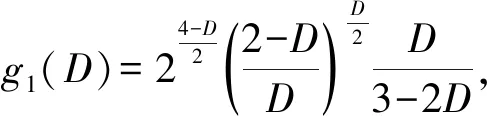
4 齿轮结合面的法向接触刚度分形模型
由文献[13]可知,引入了微凸体的截面接触面积,使得接触模型更加接近于实际。在机械结合面上,单个微凸体的法向接触刚度为:
(9)
根据齿轮粗糙表面微接触点的大小分布函数,构造齿轮结合面弹性接触区产生的法向接触刚度为:
(10)
此模型构成了齿轮结合面法向接触刚度的理论预估模型。对其进行量纲为一化得到:
(11)
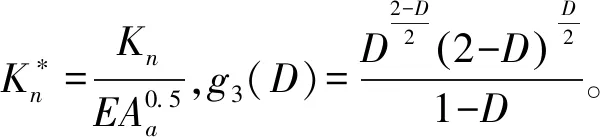
5 仿真结果
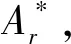
参数取值分别为:材料特性参数φ=1,0.1,0.01;k=1;表面特征尺度参数G*=10-9,10-10,10-11;分形维数D=[1.1,1.9];名义接触面积Aa=1 mm2, 大齿轮分度圆的直径R1=100 mm,小齿轮的分度圆直径R2=20,50,100 mm;接触宽度B=20 mm;综合弹性模量E=130 GPa。
由式(3)(7)(8)和式(11)建立齿轮结合面的法向载荷与法向接触刚度的关系式,通过模拟仿真分析,得法向接触载荷与法向接触刚度的关系,如图2所示,并与文献[7]和文献[3]中的模型进行比较,分析得出,同样的载荷下,文献[7]模型得出的法向刚度最大,文献[3]模型得出的法向刚度最小,这是因为文献[7]模型假设为一个粗糙平面和一个光滑平面的接触,而齿轮啮合面的接触为曲面接触,因此文献[7]模型得出的结果要高于其他两个模型的结果。而文献[3]提出的圆柱体结合面法向接触模型,虽然已经考虑了曲面接触,但是未考虑域扩展因子,在建立模型时将最大接触面积与粗糙表面的接触面积之比近似为1,得到的模型精度不高,因此得出的法向刚度低于本文提出的模型结果。而本文提出的齿轮结合面分形模型,既考虑了齿轮啮合的曲面接触,又考虑了域扩展因子的影响,并引入了微接触截面积,使得模型更加准确。
5.1 分形维数D对齿轮结合面法向接触刚度的影响
改变分形维数D,其余参数不变,得出法向载荷与法向刚度之间的关系,如图3所示。可以看出:分形维数较低时,法向载荷与法向刚度之间近似呈线性关系,且随分形维数的增加,法向刚度也随之增加;而分形维数较高时,法向载荷与法向刚度之间呈线性关系。分形维数存在一个临界值,当分形维数D>1.7时,法向刚度随分形维数的增加而减小;当D<1.7时,法向刚度随分形维数的增加而增加。同时可以看出,增加法向载荷有利于提高法向接触刚度。


图3 不同分形维数D的法向载荷与法向刚度之间的关系(G*=10-10,φ=1,R1=100 mm,R2=50 mm)
5.2 表面特征长度尺度系数对齿轮结合面法向接触刚度的影响
改变表面特征长度尺度系数G*,其余参数不变,得出法向载荷与法向刚度之间的关系,如图4所示。通过图4可以看出:法向接触刚度随着表面特征长度尺度系数的增加而减小,说明表面特征长度尺度系数越大,接触的两表面越粗糙,结合面的法向接触刚度就越小,即可以通过减小齿轮结合面的粗糙度,提高齿轮结合面的法向接触刚度。
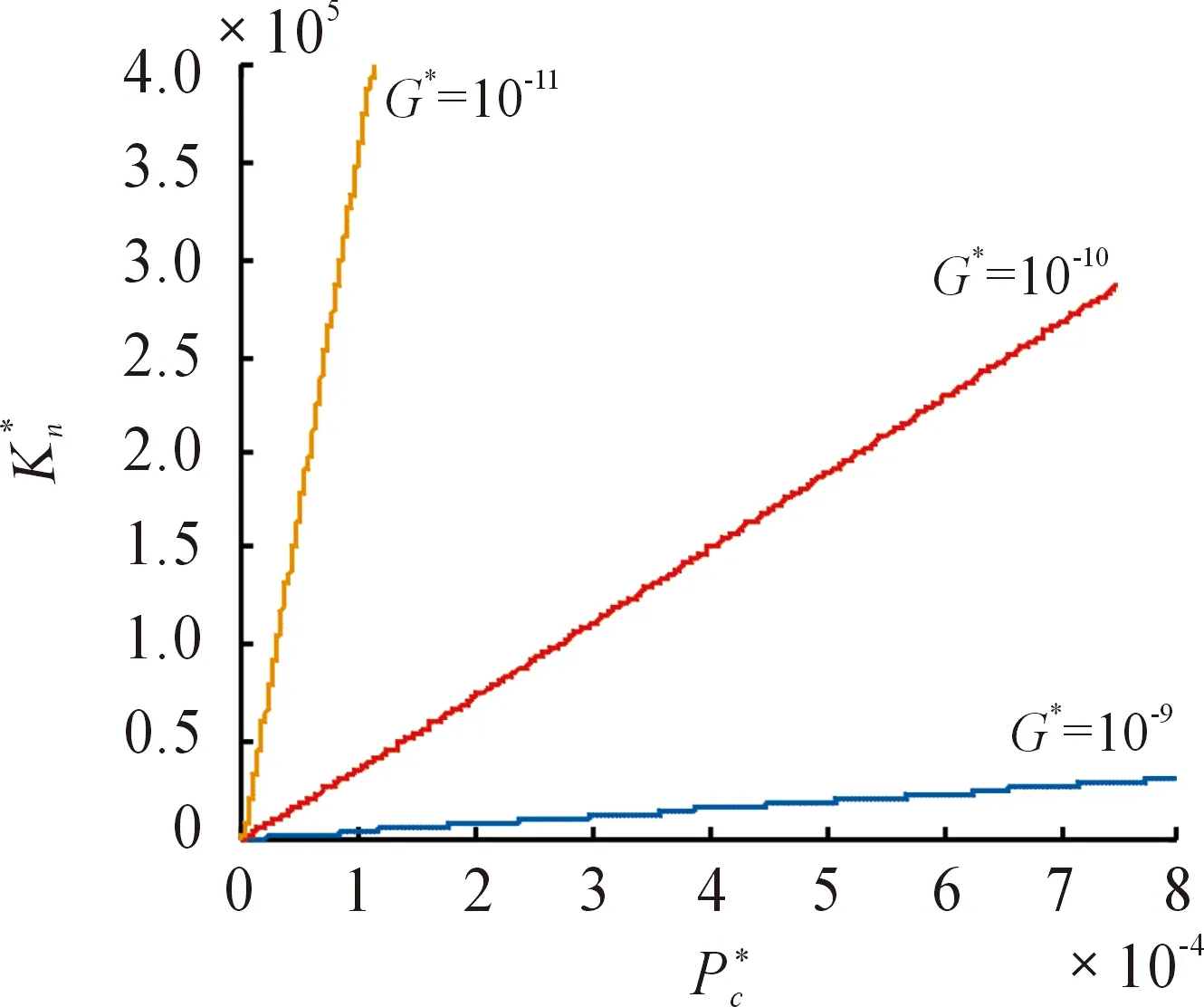
图4 不同表面特征长度系数的法向载荷与法向刚度之间的关系
5.3 材料特性参数对齿轮结合面法向接触刚度的影响
改变材料特性参数φ,其余参数不变,得出法向载荷与法向刚度之间的关系,如图5所示。通过图5可以看到:法向接触刚度随着材料特性参数的增大而增大,因为φ=σy/E,可以通过提高材料的屈服强度或减小弹性模量,来提高齿轮结合面的法向接触刚度。
5.4 齿轮分度圆半径对齿轮结合面法向接触刚度的影响
改变小齿轮的分度圆直径R2,其余参数不变,得出法向载荷与法向刚度之间的关系,如图6所示。可以看出,增加齿轮的分度圆半径,可以提高结合面的法向接触刚度,根据d=mz,可以通过增加齿轮的齿数或是增加齿轮的模数来提高齿轮结合面的法向接触刚度。
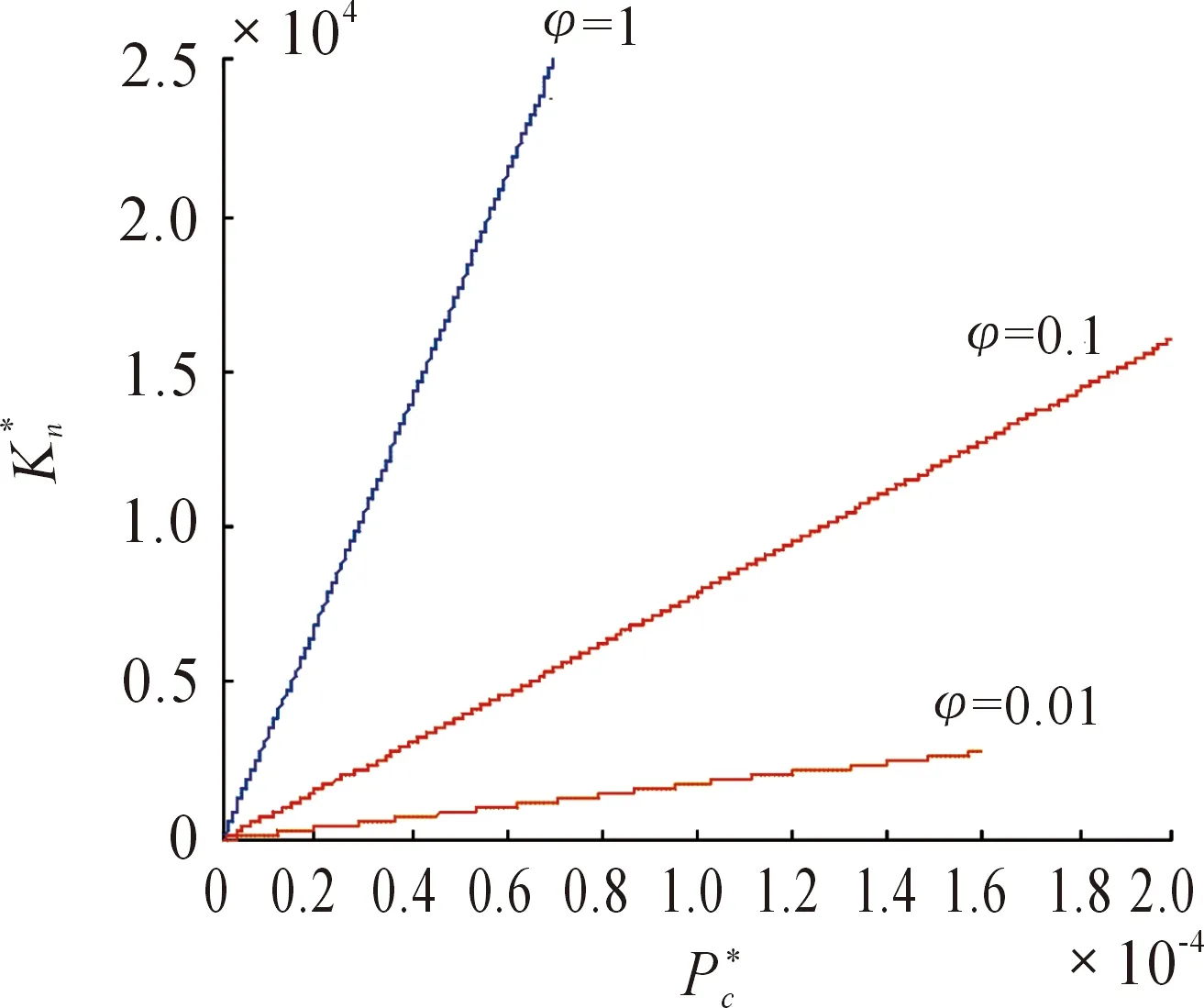
图5 不同材料特性参数的法向载荷与法向刚度之间的关系
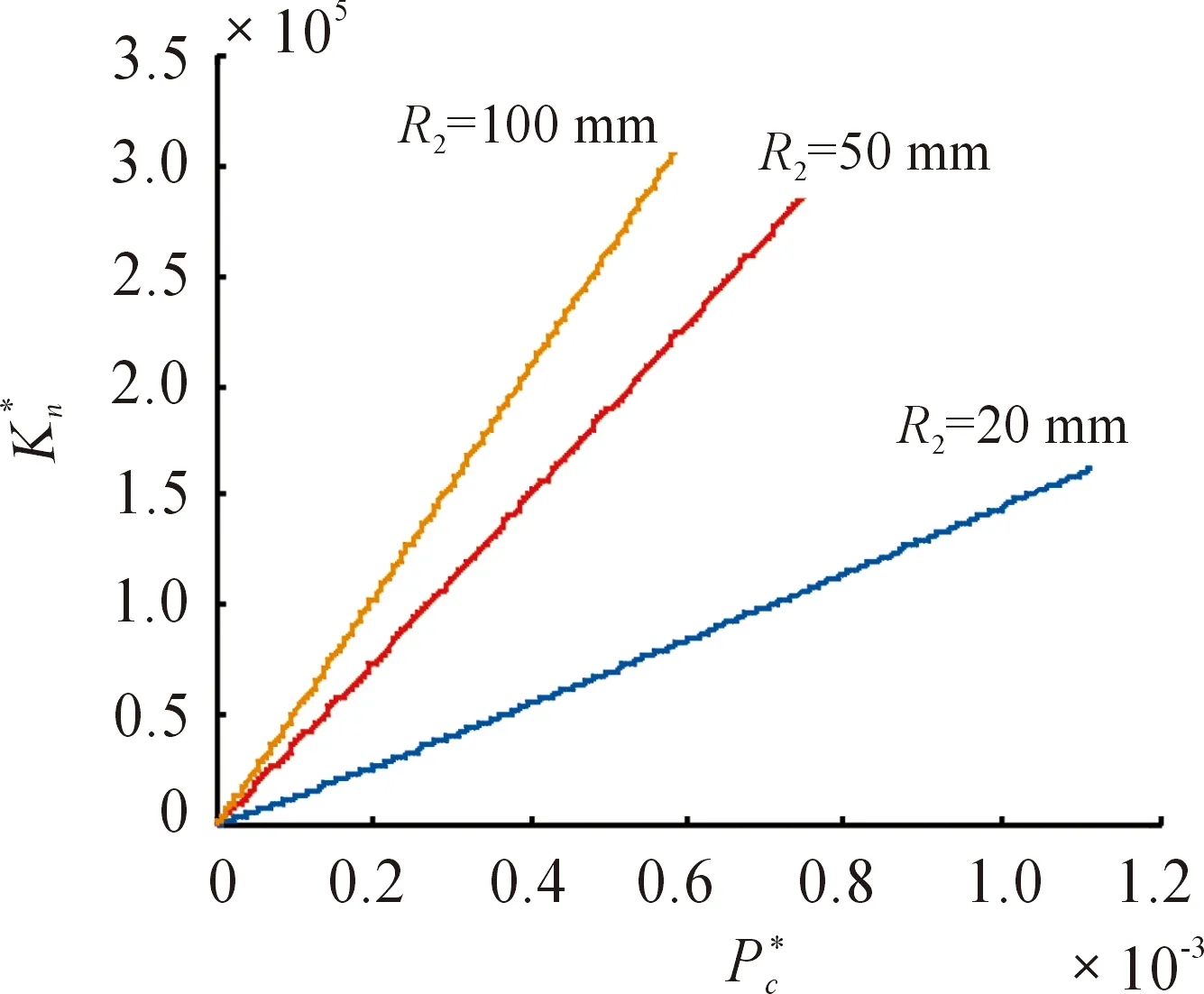
图6 不同齿轮分度圆半径的法向载荷与法向刚度之间的关系
6 结论
提出了一种新的齿轮结合面法向接触刚度预估模型,考虑了域扩展因子的影响,并引入了微接触截面积,使得模型更加准确。
仿真分析得出:分形维数比较小时,法向载荷与法向刚度之间近似呈线性关系,且随分形维数的增加,法向刚度也随之增加;而分形维数较高时,法向载荷与法向刚度之间呈线性关系。分形维数存在一个临界值,当分形维数D>1.7时,法向刚度随分形维数的增加而减小,当D<1.7时,法向刚度随分形维数的增加而增加;增加法向载荷有利于提高法向接触刚度。法向接触刚度随着表面特征长度尺度系数的增加而减小;法向接触刚度随着材料特性参数的增大而增大;增加齿轮的分度圆半径,可以提高结合面的法向接触刚度。
以上结论对于指导齿轮设计具有重要的实践意义,在确定齿轮表面的参数时,需要根据齿轮实际的受载和工况,计算表面粗糙度的最优值;通过选取齿轮材料(提高屈服强度或减小弹性模量);增加齿轮的模数或齿数,都能够提高齿轮结合面的法向接触刚度,在一定程度上能够对齿轮结合面接触特性进行理论预测,从而有效降低齿轮成本。

