基于格点型有限体积法的滑动轴承油膜压力特性分析

杨国栋, 曹贻鹏, 明平剑, 张文平, 李燎原

(1.哈尔滨工程大学 动力与能源工程学院，哈尔滨 150001； 2.中国舰船研究设计中心，武汉 430064)

滑动轴承是最常见的流体润滑轴承，具有形式简单、接触面积和承载力大等优点，在工业领域中广泛应用[1]。当轴颈转动时，轴与轴瓦之间的楔形间隙内会形成一层动压液膜，起到平衡外载荷和减小摩擦损耗的作用。

雷诺方程是求解轴承油膜压力的核心方程，其求解方法主要有解析法、有限差分法(FDM)、有限元法(FEM)等[2]。解析法只适用于无限短或无限长轴承，此时雷诺方程退化为一维方程，无法准确描述轴承内的压力分布；FDM是最常用的数值解法，形式简单，方程中的偏导数项可以通过差商形式表示，润滑区域的离散采用正交化的四边形网格，Sun等[3-10]基于该算法研究了滑动轴承的润滑特性，但是对于结构复杂的润滑区域，无法采用该算法求解；FEM是从弹性力学发展而来的算法，之后应用于润滑计算领域[11-15]，润滑区域的划分可以采用非结构化网格，单元大小和节点数可以任意选取，对润滑区域形状的要求较少，但是该算法需要构建一个总刚矩阵，计算量较大。

格点型有限体积法(Cell-Vertex Finite Volume Method，下面用CVFVM表示)是CFD领域中常用的方法，该算法既具有有限体积法强守恒性的特点，又具有FEM对网格类型灵活性的特点，近些年来在传热和+结构等领域也有较多的应用[16-17]，但是在润滑领域应用较少。

本文基于CVFVM离散雷诺方程，并利用矢量化方式推导得出了适用于非结构化网格的方程形式，并对文献[3]中的算例进行了对比和验证，在此基础上，研究了偏心率和轴颈倾斜角度对内燃机主轴承压力特性的影响。

1 理论方程

1.1 雷诺方程

在润滑现象的研究中，雷诺方程的求解是关键步骤，不可压缩流体润的瞬态雷诺方程如下

(1)

式中:θ为周向角度坐标，degree;z为轴承宽度坐标，m;R为轴承半径，m;p为油膜压力，Pa;h为油膜厚度，m;U为轴颈速度，m/s;η为润滑油黏度，Pa·s。

根据下式进行无量纲化

(2)

式中:B为轴承宽度，m;c为轴承间隙，m；φ偏位角，degree;ε为偏心率。

可得

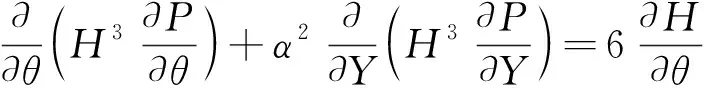
(3)

为了使式(3)适用于非结构化网格，雷诺方程转化为矢量形式如下

▽·(Γ▽p)=Φs

(4)

其中

式中:Γ为压力系数；Φs为源项。

1.2 液膜厚度方程

设轴心坐标为(x,y)，径向滑动轴承的液膜厚度可用下式表示

h=c+ecos(θ-φ)=

c+ecosφcosθ+esinφsinθ=

c+xcosθ+ysinθ

(5)

式中:e为偏心距。

无量纲形式为

H=1+Xcosθ+Ysinθ

(6)

X=x/c;Y=y/c

(7)

油膜厚度位置对坐标和时间的导数，可用如下形式表示

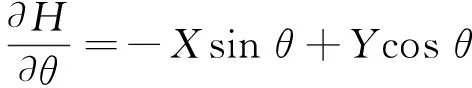
(8)

因此，源项的另一种表达如下

Φs=6(-Xsinθ+Ycosθ)

(9)

2 雷诺方程的离散

2.1 方程的积分形式

在控制体内，对式(4)进行积分可得

(10)

式中:V为控制体体积。

2.2 方程的离散

CVFVM算法将有限体积法(FVM)的守恒性和有限单元法(FEM)处理非结构单元的灵活性结合在了一起。其控制体是围绕节点构成，节点储存压力P，其他变量存储在单元中心，如图1所示。

图1 CVFVM 控制体示意图

根据高斯散度定理，将体积分转化为面积分并进行离散可得

(11)

式中:nc为节点周围的单元数；ncni为第i个单元的节点总数；j为单元内的节点编号；N为形函数；α为x和y两个坐标方向；S为围绕控制体的积分线。

假设源项在单元内均匀分布

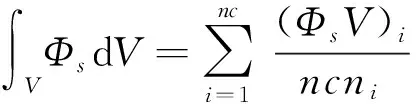
(12)

最终，式(10)可转化为

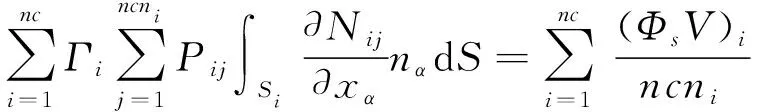
(13)

2.3 形函数积分的求解

本算法目前采用两种单元形式：常应变三角形单元和双线性四边形单元，下面分别给出各个单元形函数导数积分的推导过程：

2.3.1 常应变三角形单元

三角形单元的示意图如图2所示。

三角形单元形函数

N1=1-ξ-η;N2=ξ;N3=η

(14)

式中:ξ,η为局部坐标系中的坐标。

整体坐标系下的坐标可用下式表示

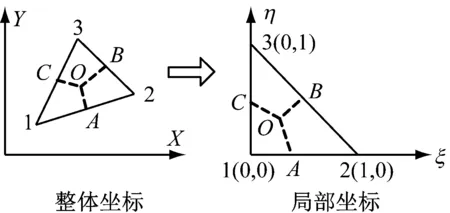
图2 任意三角形单元的坐标转换

y=y1N1+y2N2+y3N3

(15)

其中，(x1,y1)、(x2,y2)、(x3,y3)为整体坐标系下三个节点的坐标。

节点周围的第i个单元内，形函数导数沿控制体边界的积分为

(16)

式中:j为单元的节点编号；Lijα为第i个单元围绕第j个节点的积分线在α方向上的投影长度。

形函数在全局坐标下的导数如下

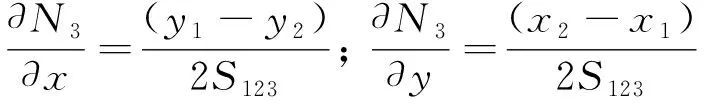
(17)

各条积分线的长度可用式(18)求解

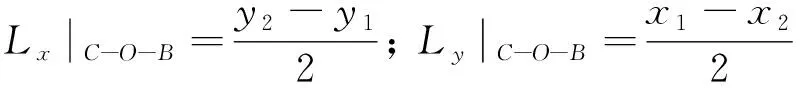
(18)

2.3.2 双线性四边形单元

四边形单元的示意图如图3所示。

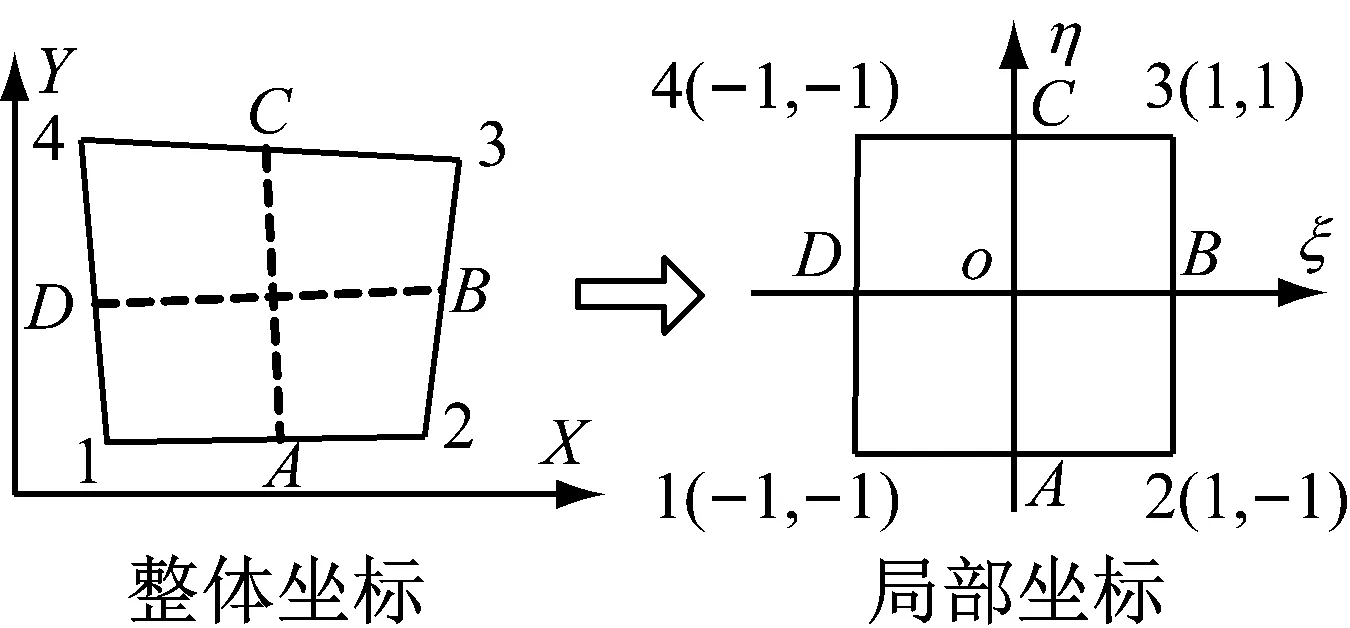
图3 任意直边四边形单元的坐标转换

四边形单元形函数

(19)

整体坐标可用下式表示

x=x1N1+x2N2+x3N3+x4N4

y=y1N1+y2N2+y3N3+y4N4

(20)

式中：(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4) 分别为四边形节点1,2,3,4在全局坐标系下的坐标。

形函数围绕节点1的线积分

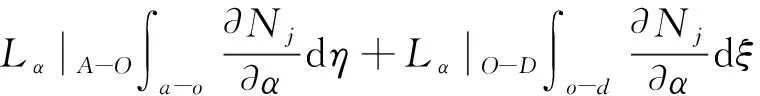
(21a)

形函数围绕节点2的线积分

(21b)

形函数围绕节点3的线积分

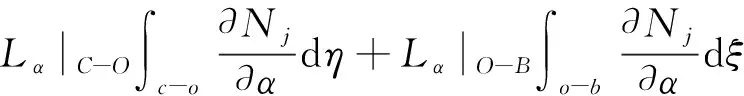
(21c)

形函数围绕节点4的线积分

(21d)

线积分的投影长度可以用下式表示

Lx|AO=(x3+x4-x1-x2)/4

Ly|AO=(y3+y4-y1-y2)/4

Lx|BO=(x1+x4-x2-x3)/4

Ly|BO=(y1+y4-y2-y3)/4

Lx|CO=(x1+x2-x3-x4)/4

Ly|CO=(y1+y2-y3-y4)/4

Lx|DO=(x2+x3-x1-x4)/4

Ly|DO=(y2+y3-y1-y4)/4

(22)

3 算例验证

本文的计算程序是在哈尔滨工程大学动力装置工程技术研究所自主开发的通用输运方程求解器GTEA软件的基础上开发的，采用Fortran90语言编程，在参数为4 GB RAM、Intel Core i5-2400、CPU3.1 GHz的计算机中运行程序，采用Gambit等网格划分软件进行网格划分，通过GTEA的前处理模块读入网格信息。为了验证该算法的适用性和精度等特点，本文采用文献[3]中的径向滑动轴承算例，分别计算了不同工况下的压力结果，轴承参数如表1所示。

3.1 压力分布的对比

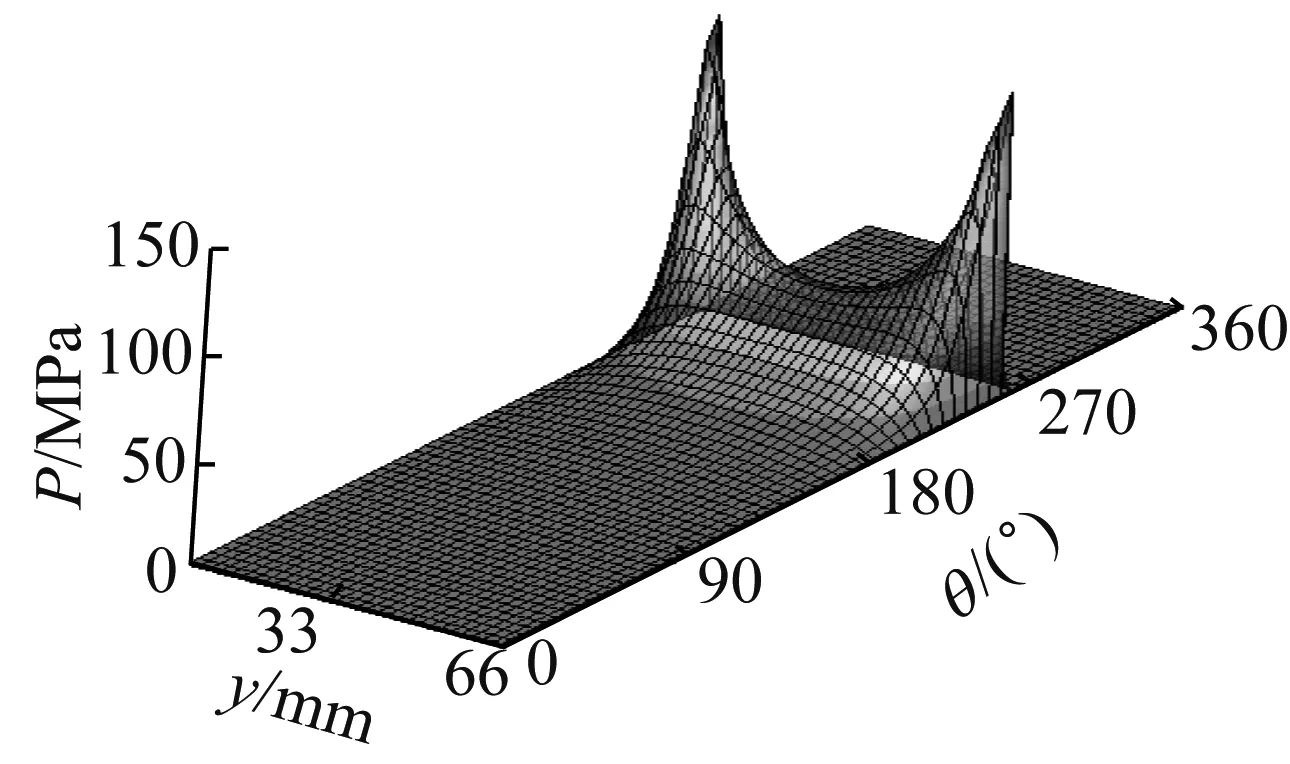
本节分别选用0.01°和0.03°工况下的压力分布结果进行对比，计算模型的偏位角均为90°。具体结果如图4～图6所示。

表1 轴承基本参数

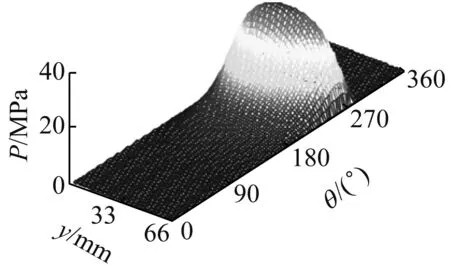
(a) 参考值

(b) 当前值

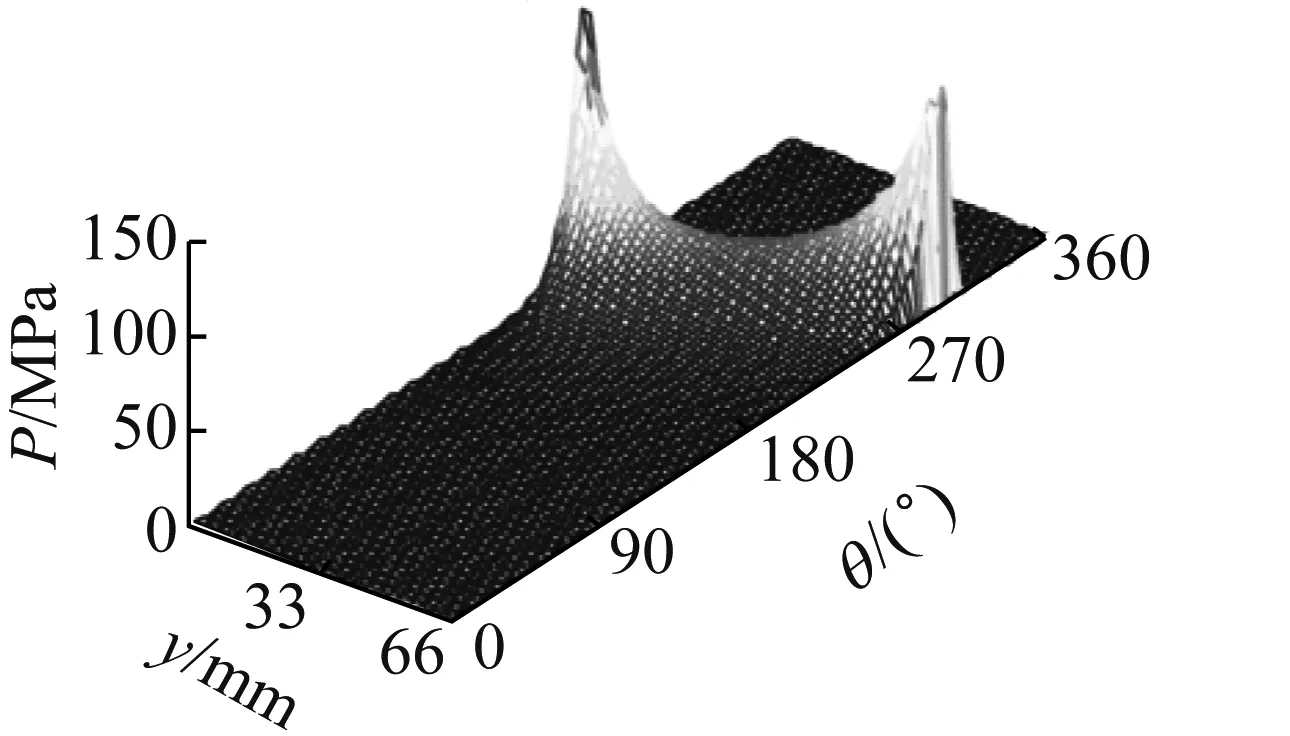
(a) 参考值

(b) 当前值

(a) 倾斜角=0.01°

(b) 倾斜角=0.03°

由图4～图5可知，不同倾角情况下，主压力区均出现在90°～270°之间，与偏位角值相对应；倾斜角为0.01°时，压力在轴承中截面处最大，并沿两侧方向之间减小；倾斜角为0.03°时，压力在轴承两个端面处最大，并沿中间位置方向逐渐减小。

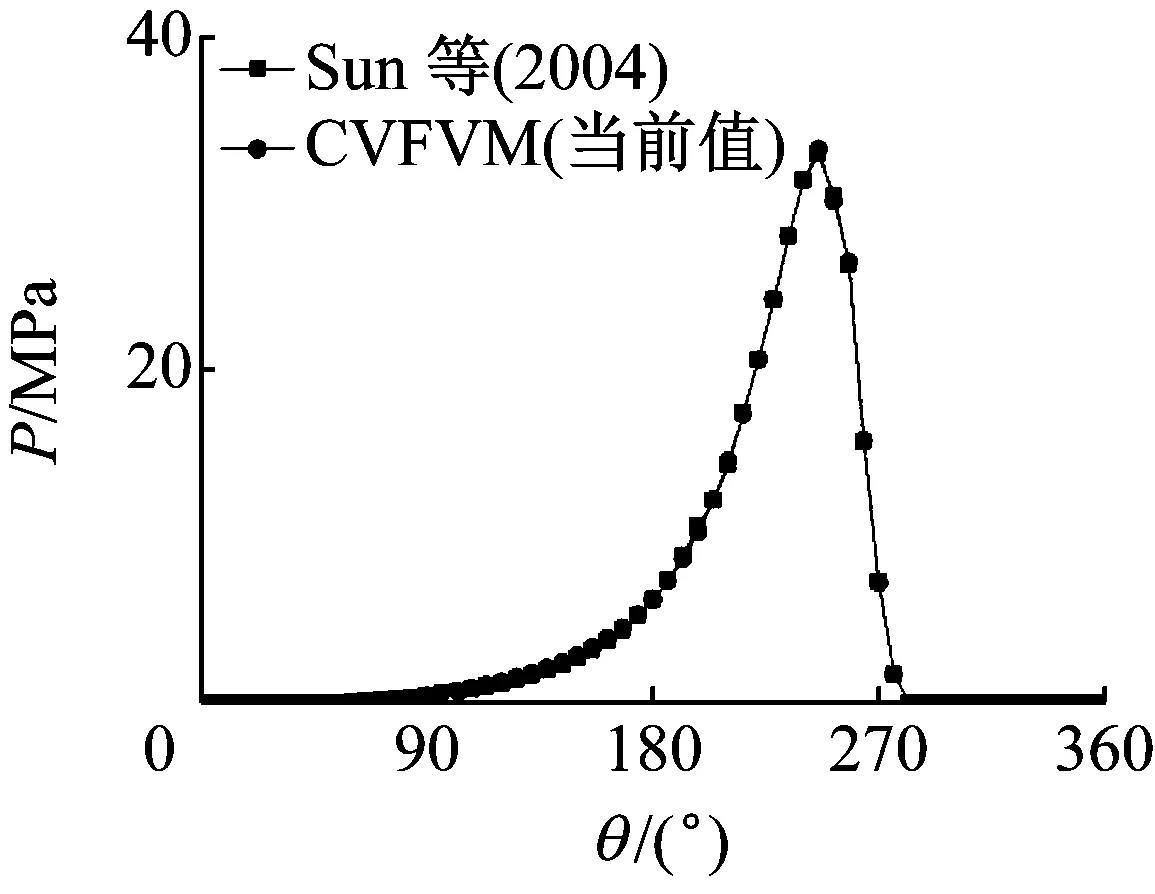
由于当倾斜角为0.01°时，最大压力值出现在轴承中截面附近，因此取33 mm处的压力分布进行对比，当倾斜角为0.03°时，最大压力出现在轴端端部附近，因此取63.8 mm处的压力值进行对比。如图6所示，在两个倾斜角情况下，CVFVM算法的结果与参考值基本一致。

由表2可知，在不同倾角下，CVFVM算法与参考结果下的做大压力值基本一致，最大误差0.67%。

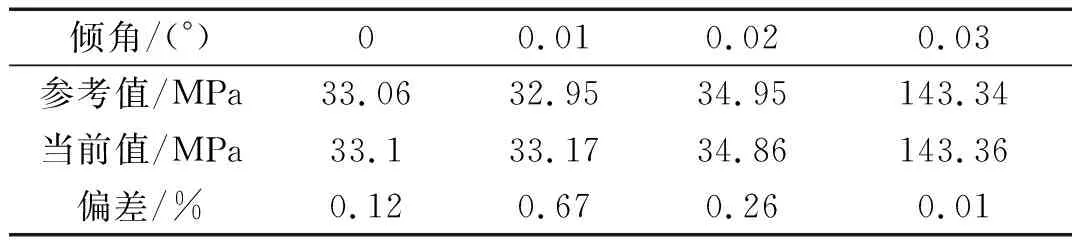
表2 峰值压力的对比

经过上面的对比分析，说明CVFVM用于雷诺方程的求解是适用的，同时也能保证较好的计算精度。

3.2 网格适应性的验证

由于雷诺方程的离散过程是采用矢量化方式推导的，因此该算法对于非结构化网格有很好的适应性，同时，基于有限体积法的强守恒特性，也可通过合理分配求解域的网格密度来提高计算效率。下面分别采用不同密度的四边形网格和三角形网格划分计算域，进而对上述两个特点进行验证。表3给出了不同模型的网格参数及计算耗时，其中Quad表示四边形网格，Tri代表三角形网格，计算结果如图7所示。

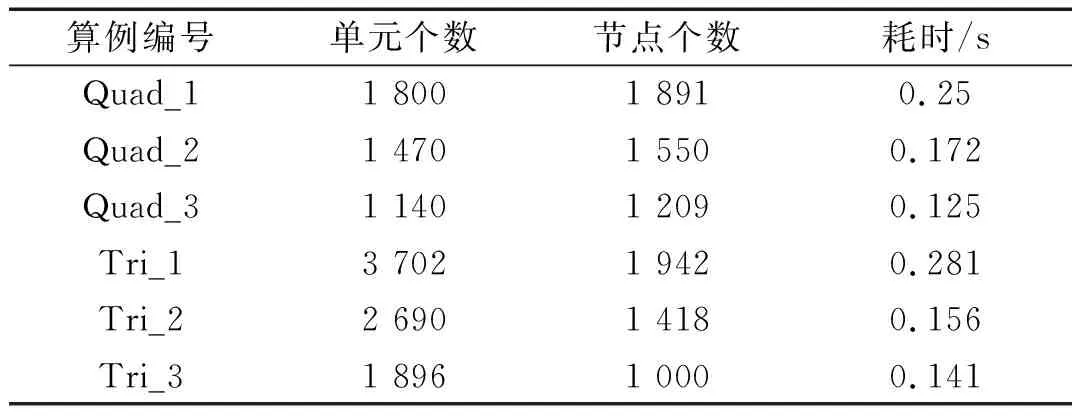
表3 不同算例的网格参数及耗时

(a) Quad_1

(c) Quad_3

图7中，方框区域内油膜压力值及梯度值较大，在油膜压力分析中为重点研究的区域，因此，保持该区域网格密度不变，分别逐步减小该区域两侧的网格密度。由图7可知，无论采用四边形网格还是三角形网格划分区域，油膜压力分布基本一致；同时由表3可知，随着两侧网格密度的减小，节点数逐渐下降，相应模型的计算时间逐渐减小。由此，CVFVM算法对非结构化网格的适应性及对计算效率的提高得以验证。

4 内燃机主轴承压力特性求解

主轴承是内燃机结构中的关键部件，其压力特性的求 解是整机润滑性能分析的关键组成部分，本节选用的主轴承参数如下表4所示，主要用于分析偏心率和轴颈倾角对压力特性的影响，其中偏位角为0°。

表4 内燃机主轴承参数

由图8可知，随着偏心率的增大，最小油膜厚度逐渐减小，同时最大油膜压力逐渐增大，在偏心率在0.7～0.9之间变化时，液膜压力的增大更为明显。

(a) 油膜厚度的变化

(b) 油膜压力的变化

由图9可知，随着轴颈倾斜角的增大，轴承端部附近的油膜厚度逐渐较小，油膜压力的峰值由中间位置逐渐向轴承端部移动，同时液膜压力的幅值逐渐增大。

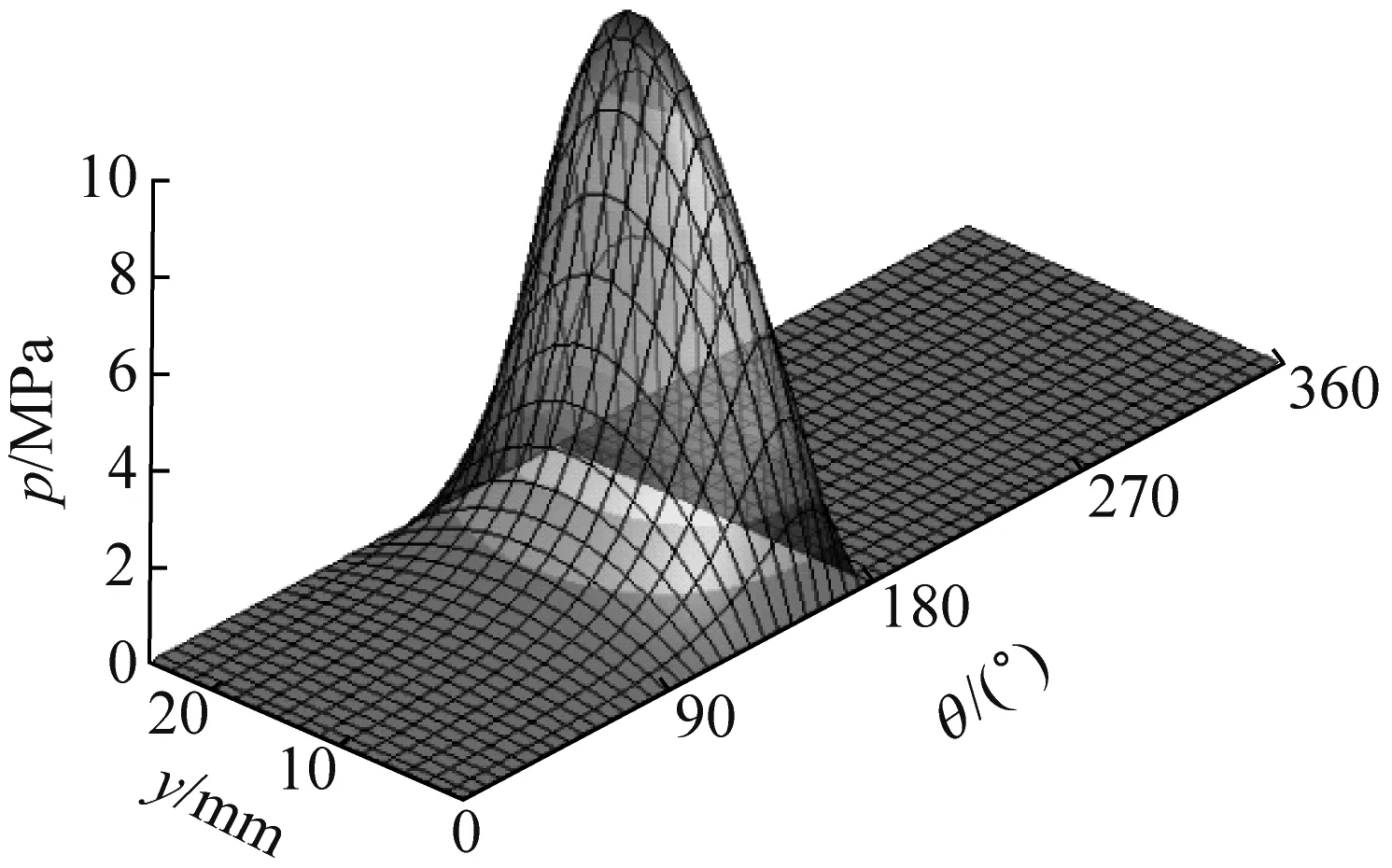
(a) 倾斜角0.01°

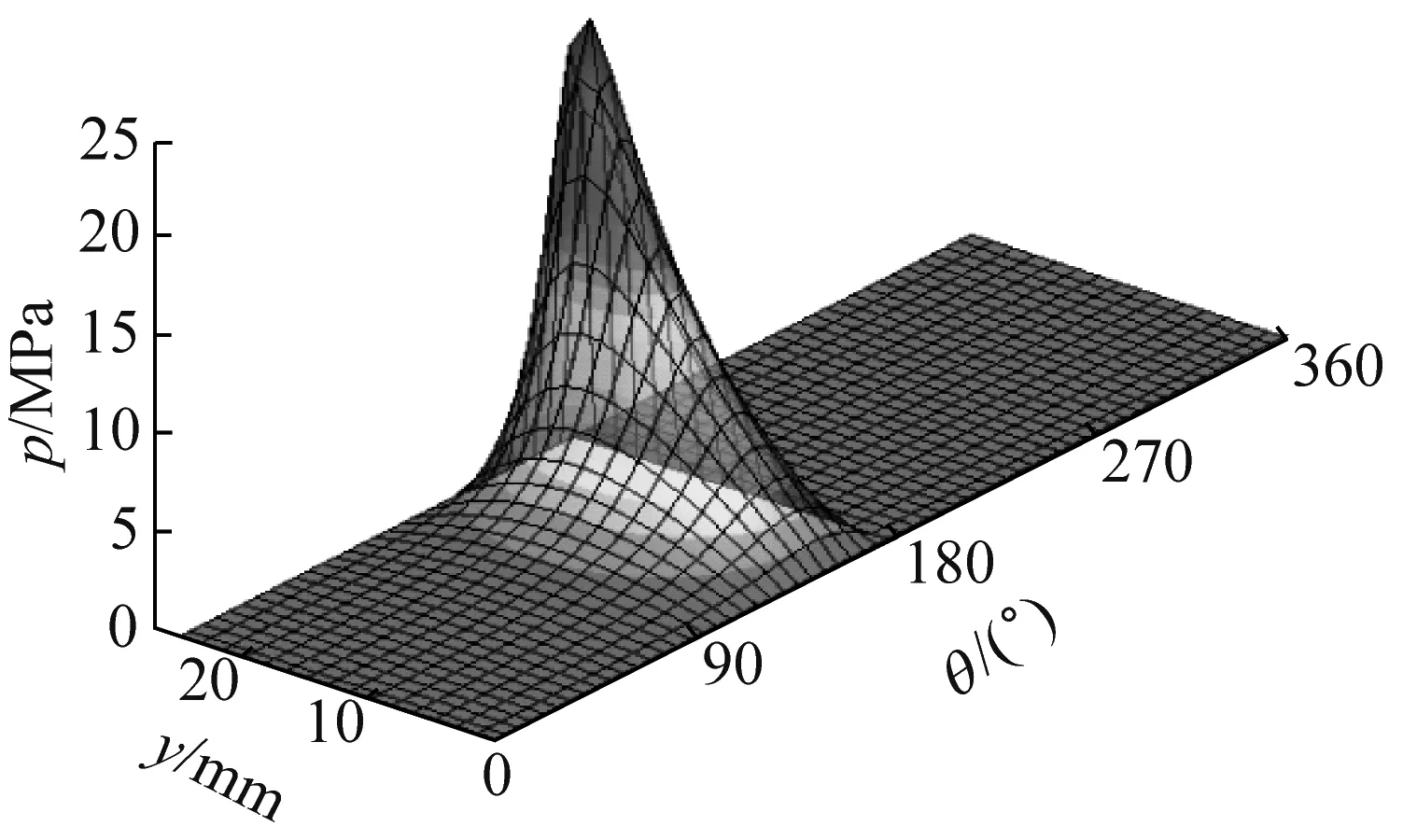
(c) 倾斜角0.03°

5 结 论

本文基于格点型有限体积法，并采用矢量化方式离散和求解了雷诺方程，通过对不同工况下滑动轴承润滑算例的对比和分析，得出以下结论：

(1) CVFVM算法用于求解雷诺方程是合理可行的，同时计算精度满足要求。

(2) 与文献[3]方法相比，CVFVM算法可用于处理非结构化网格划分的求解域，因此可用于计算几何形状复杂的润滑区域。

(3) 由于有限体积法对局部区域强守恒性的特点，可以通过对润滑区域网格密度的合理分配来提高计算效率。

(4) 主轴承的偏心距的增大会引起轴承油膜压力峰值的增大，轴颈倾斜角的增大会导致峰值压力向端部移动，会加快轴承端部的磨损。