超磁致伸缩激振器的结构优化及动态性能研究

王安明， 孟建军， 胥如迅 ， 何昌雪

(1.兰州交通大学 机电工程学院，兰州 730070； 2.兰州交通大学 机电技术研究所，兰州 730070；3.甘肃省物流及运输装备信息化工程技术研究中心，兰州 730070； 4.西安铁路职业技术学院 牵引动力学院，西安 710026)

振动时效是利用激振器给金属工件在其固有频率下施加一定时间的振动，以消除和匀化内部残余应力的一种工艺技术。与热时效和自然时效相比，具有低能耗、低成本、高效率、绿色环保等突出优点，已成为降低金属工件残余应力的标准工艺[1-3]。目前，传统的电机式激振器在国内外振动时效应用中占有很大比例。这种激振器主要的不足是振动频率低，很难达到工件的固有频率，时效效果不理想；可靠性低，寿命短，高速振动时易飞车；自动化程度低，振动频率不能平滑调节；能耗高，经济性差。鉴于传统激振器在实际应用中存在的不足，研究、开发新材料、新结构的激振器对振动时效技术的进一步推广，推动振动时效技术更新换代乃至产业升级，具有较高的应用价值。

磁致伸缩效应是在交变磁场作用下铁磁材料产生微小应变的现象。磁致伸缩系数高于10-3的材料叫作超磁致伸缩材料(Giant Magnetostrictive Material，GMM)[4]。GMM是一种性能优越的智能材料，其能量密度可达2.5×10-2J/cm3，响应时间<1 μs，能实现1 kN的输出力，其单晶结构性能更为优异[5]。此外，GMM高达0.75的机电耦合系数决定了它有比压电陶瓷材料更高的换能效率，振动频率可至数千赫兹，这些优良的性能表明它是振动时效设备理想的激振源之一。

超磁致伸缩材料的磁滞模型、激振器的磁路设计、温度控制、预压应力及输出机构决定着激振器的性能。近年来，国内外研究学者针对超磁致伸缩激振器进行了广泛而深入的研究，取得了丰富的研究成果。目前，针对激振器的动态性能研究较少，有待进一步深入。因此，在相关研究成果的基础上，针对超磁致伸缩激振器驱动线圈采用细导线、多匝数、小电流的设计方案造成其时间常数大、电流上升率小、动态性能差的问题，采用了减少匝数、增加线径、大电流驱动的设计方案，以提高激振器的动态性能。激振器驱动线圈设计为双线圈并联结构，偏置磁场由驱动电流叠加的直流分量产生，采用棒叠片式GMM棒，优化驱动线圈几何尺寸，对内部磁场进行有限元分析，在MATLAB环境下仿真激振器的阶跃响应，实验验证激振器的幅频特性，最后分析振动时效应用效果。

1 超磁致伸缩激振器的结构及其驱动原理

1.1 基本结构

超磁致伸缩激振器主要由驱动线圈、GMM棒、导磁盖、导磁壁、导磁体、输出杆、预紧弹簧、预紧螺母、底座和外壳等组成，其结构如图1所示。其中GMM棒、驱动线圈、导磁盖、导磁壁和导磁体组成闭合磁路，以改善GMM棒内部磁场的均匀性，而外壳、底座、预紧螺母和输出杆采用非导磁材料，以降低漏磁。预紧弹簧给GMM棒施加预紧力，预紧力的大小通过预紧螺母调节，从而得到最佳的磁致伸缩应变。预紧弹簧采用碟形弹簧，刚度几乎不变且压力稳定[6]。

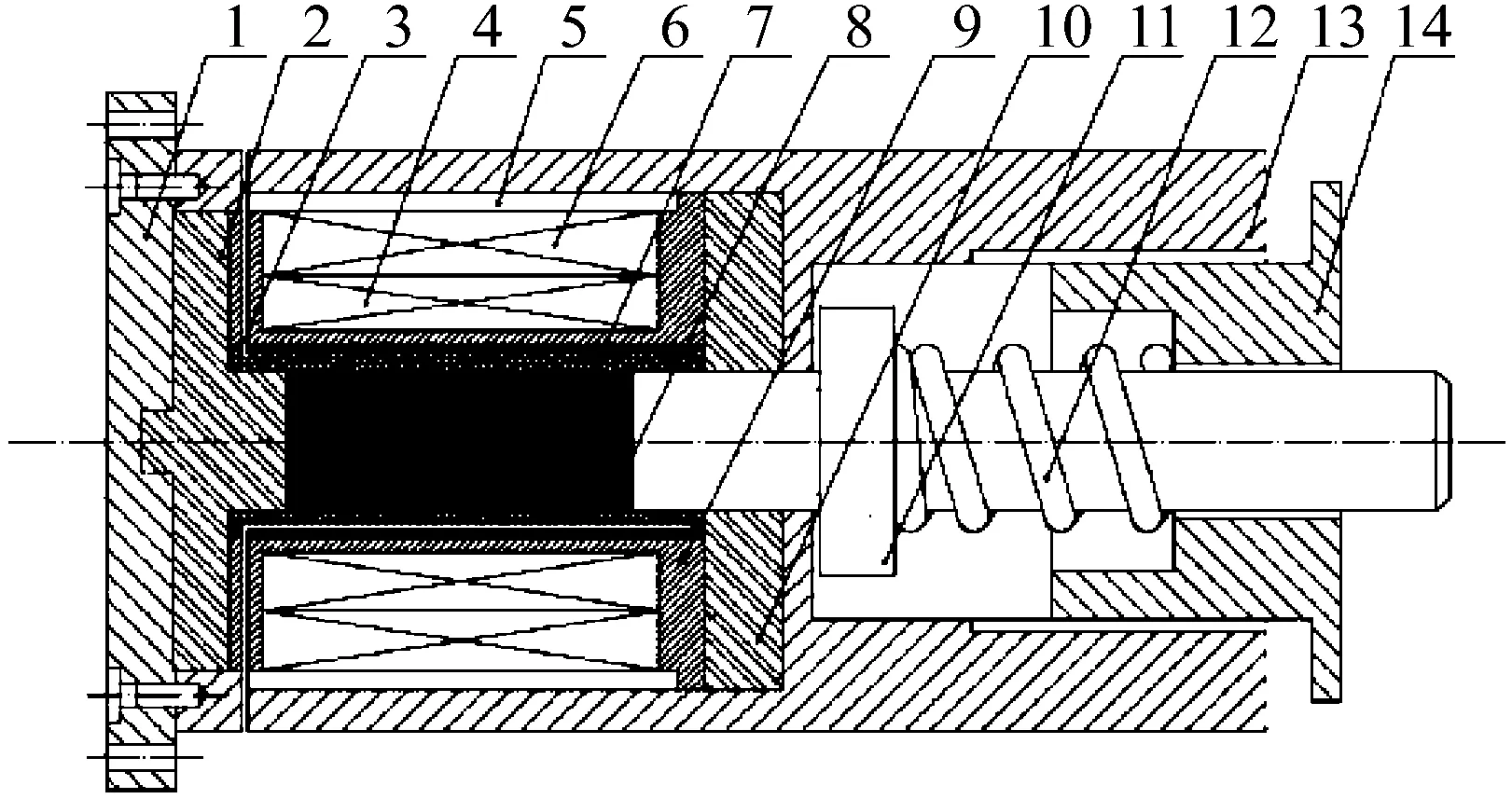
1．底座；2．下导磁盖；3．套筒；4．驱动线圈Ⅰ；5．导磁内壁；6．驱动线圈Ⅱ；7．GMM棒；8．导磁体；9．线圈骨架；10．上导磁盖；11．输出杆；12．预紧弹簧；13．外壳；14．预紧螺母

1.2 驱动原理

GMM棒在交变磁场的作用下输出频率是激励频率的2倍，即输出存在倍频效应。倍频效应增加了激振器的高次谐波分量，增大了总谐波失真[7-8]。为了消除倍频效应，采用驱动电流叠加直流分量的方法给GMM棒提供偏置磁场，方波驱动电压如图2所示。

图2 方波驱动电压

通常，在GMM棒长度确定的情况下，为了获得较大的磁场强度以提高激振器的输出位移，驱动线圈采用增加匝数、减小线径、小电流驱动的方法。这种方法虽然减小了驱动电流，却使驱动线圈的电感增加、时间常数增大、电流上升率受到限制，降低了激振器的动态性能。为此，采用减少驱动线圈匝数、增大驱动线圈线径、大电流驱动的方案。驱动线圈Ⅰ和驱动线圈Ⅱ并联，以减小电感，改善作动器的动态性能。

2 激振器的结构设计与磁路优化

2.1 GMM预压应力的选择

GMM棒抗拉强度约为28 MPa，抗压强度约为700 MPa，且脆性大，为避免在工作时承受拉应力，应对 GMM 棒加载预压应力；此外，施加适当的预压应力，低磁场强度时的磁致伸缩系数能得到明显提高[9]。

在不施加预压应力，即σ=0时，变形量明显偏小，而在一定预压应力下，变形量显著变大，变形量λ与磁场强度H呈非线性关系。GMM在不同预压应力下的λ-H曲线如图3所示。图4为GMM机电耦合系数k33、磁场强度H、预压应力σ之间的关系。由图4可知，在一定预压应力和磁场强度范围内，机电耦合系数k33几乎不变。综合考虑图1和图2各参数之间的关系，选取预压应力σ=10 Mpa、偏置磁场强度H=40 A/m，此时机电耦合系数k33=0.6。

图3 GMM在不同预压应力下的λ-H曲线

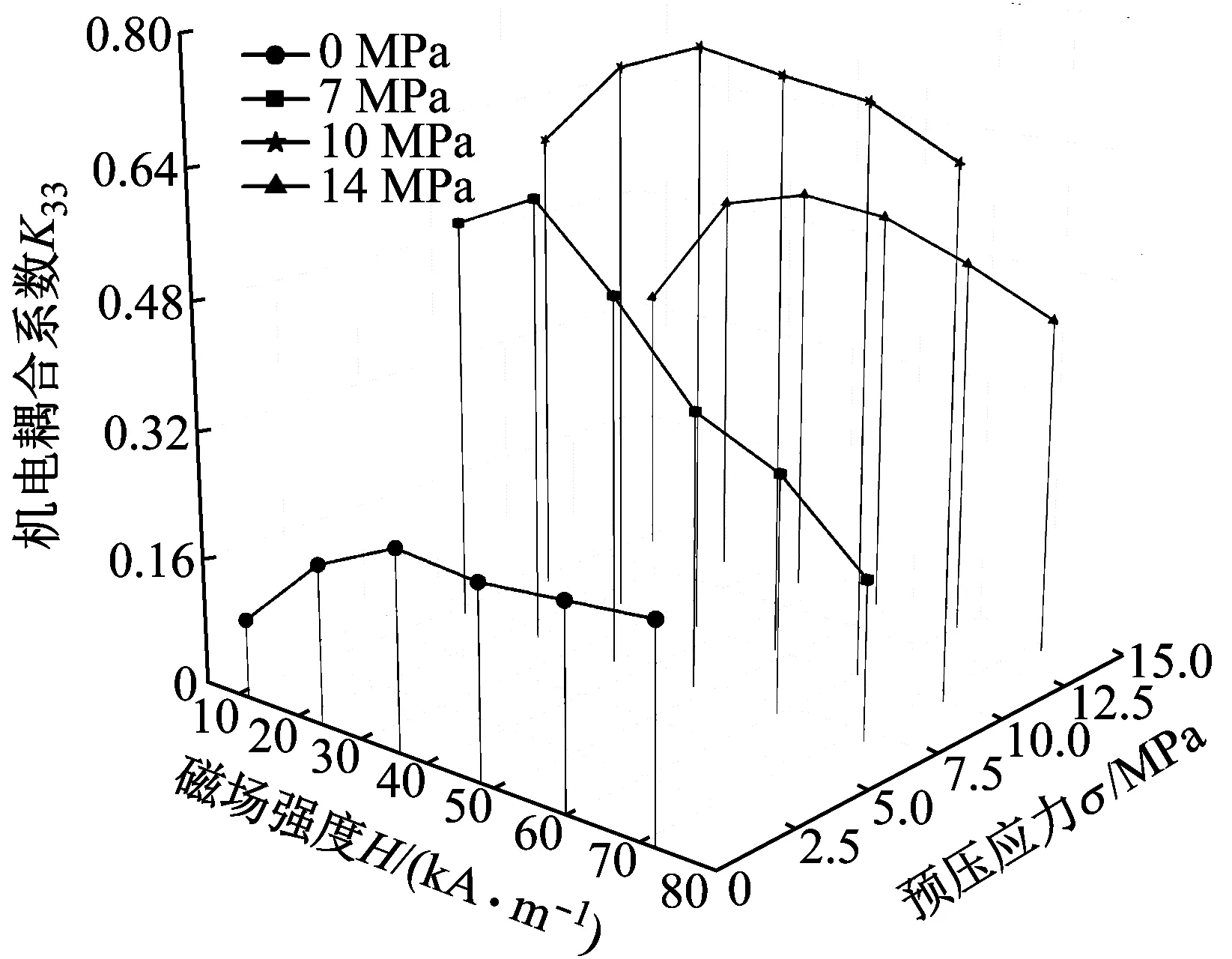
图4 预压应力σ、磁场强度H、机电耦合系数k33之间关系

2.2 GMM棒几何参数的确定

GMM棒几何形状选用圆柱体形式，主要几何参数为长度与直径，分别用lm和dm表示，其值大小决定激振器的最大输出位移xmax和Fmax最大激振力[10]，计算公式分别如下

xmax=δxs=δλslm

(1)

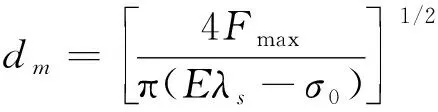
(2)

式中:xs为GMM棒磁场饱和时的伸长量；λs为GMM棒磁场饱和磁致伸缩系数；E为GMM棒的弹性模量；σ0为GMM棒的预压应力；δ为数学因子。激振器的最大输出位移xmax与最大激振力Fmax由振动时效工艺要求的输出力和位移确定。

GMM棒在交变磁场下工作时会产生涡流损耗。为此采用叠片结构的GMM以提高涡流截止频率，叠片结构的GMM棒由Terfenol-D薄片与环氧树脂粘接而成，如图5所示。叠片结构GMM棒的涡流截止频率与Terfenol-D薄片厚度的平方成反比，当外径相同时，叠片结构的GMM棒涡流截止频率是整体结构的(d/e)2倍。当工作频率相同时，GMM棒的涡流截止频率越高，损耗就越小。

2.3 驱动线圈设计及优化

激振器磁路结构中的线圈通常包括偏置线圈和驱动线圈[11]，均为多层螺线管，两者设计、计算方法相同。由于线圈发热对材料的输出特性会产生不利影响[12]。因此，应对线圈优化设计以减小发热量，抑制GMM棒的热变形，提高激振器的机电转换效率。图6中点P为线圈轴线上的几何中心，α1与α2分别代表点P与GMM棒两个端面直角顶点的夹角与水平轴线的夹角。L表示线圈的轴向长度，dr表示线圈的厚度，R1和R2分别表示线圈的内半径和外半径。

图6 多层螺线管线圈轴向结构图

多层螺线管线圈中点磁场强度为[13]

(3)

式中：N为线圈匝数；I为电流。多层螺线管线圈轴线中点上的磁场强度H和发热功耗P间的关系可由下式表示

H=G(α,β)(4P/ρR1π)1/2

(4)

式中：ρ为螺线管线圈的裸线电阻率；α=R2/R1、β=L/(2R1)、G(α,β)为螺线管线圈的几何形状因数，其值与发热功率P呈反比例关系。联立式(3)和(4)可得

(5)

当G取最大值时，磁场强度最大，发热最小，螺线管线圈电磁转换效率最高。经计算，当α=3.22，β=2.09时，G(α,β)=0.179，H=0.889NI/L。求解以kη、kβ、W为决策变量的最优化问题可得N

目标函数 Max(H)=0.889NI/L

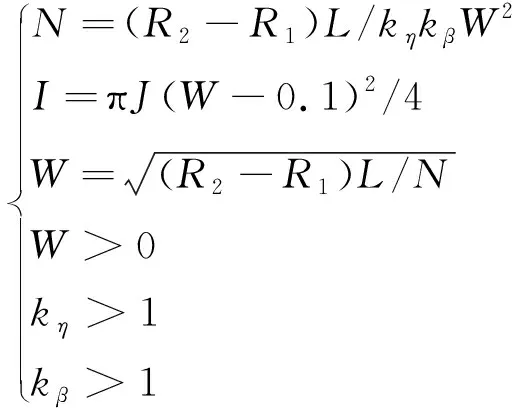
(6)

式中：kη为线圈的排绕系数；kβ为线圈的叠绕系数；W为漆包线的直径；J为电流密度。

2.4 磁路设计及优化

GMM是一种磁性功能材料，其磁致伸缩是通过磁场驱动和控制的，驱动磁场的特性对其输出特性起着决定作用[14-15]。因此，磁路设计和优化的目标是磁场强度满足位移输出的前提下，提高磁场的均匀性。

为降低漏磁、提高激振器的输出性能，把磁路结构中的各器件组成闭合磁路。由高斯磁通定律可知，无论磁介质中磁场强度与磁通密度矢量分布如何，任一闭合曲面穿出的磁通量始终等于零[16]。激振器中的磁路结构为闭合形式，磁通连续分布，可得出用磁场强度表示的如下方程

(7)

式中：N为线圈匝数；i为线圈电流值；H、Hk1、Hk2、Hk3、lk1、lk2、lk3分别代表GMM棒、上端盖、下端盖及导磁壁中的平均磁场强度与有效长度；μm、μk1、μk2、μk3、Am、Ak1、Ak2、Ak3分别代表GMM棒、上导磁盖、下导磁盖以及导磁壁中的导磁率与截面积。激振器输出位移的增大，GMM棒所处位置的磁场强度H取最大值是前提条件。

利用Comsol Multiphysics有限元软件进行参数化几何建模，用于GMM棒磁路结构的优化设计[17]。图7为磁路闭合时激振器磁感应强度云图。由图7可知，当磁路结构为闭合状态时，平均磁感应强度在GMM棒处为0.32 T，在导磁体和导磁壁的共同作用下激振器磁路内部的磁场形成了闭合回路，漏磁很少，磁轭效果更为理想。

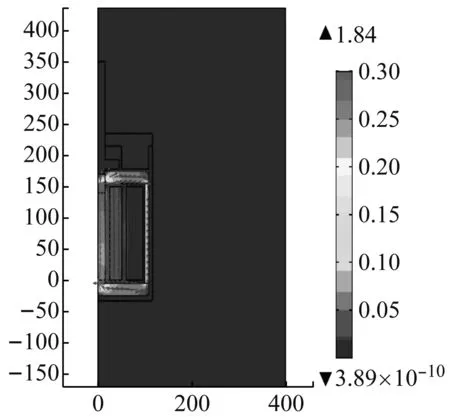
(a) 2D效果

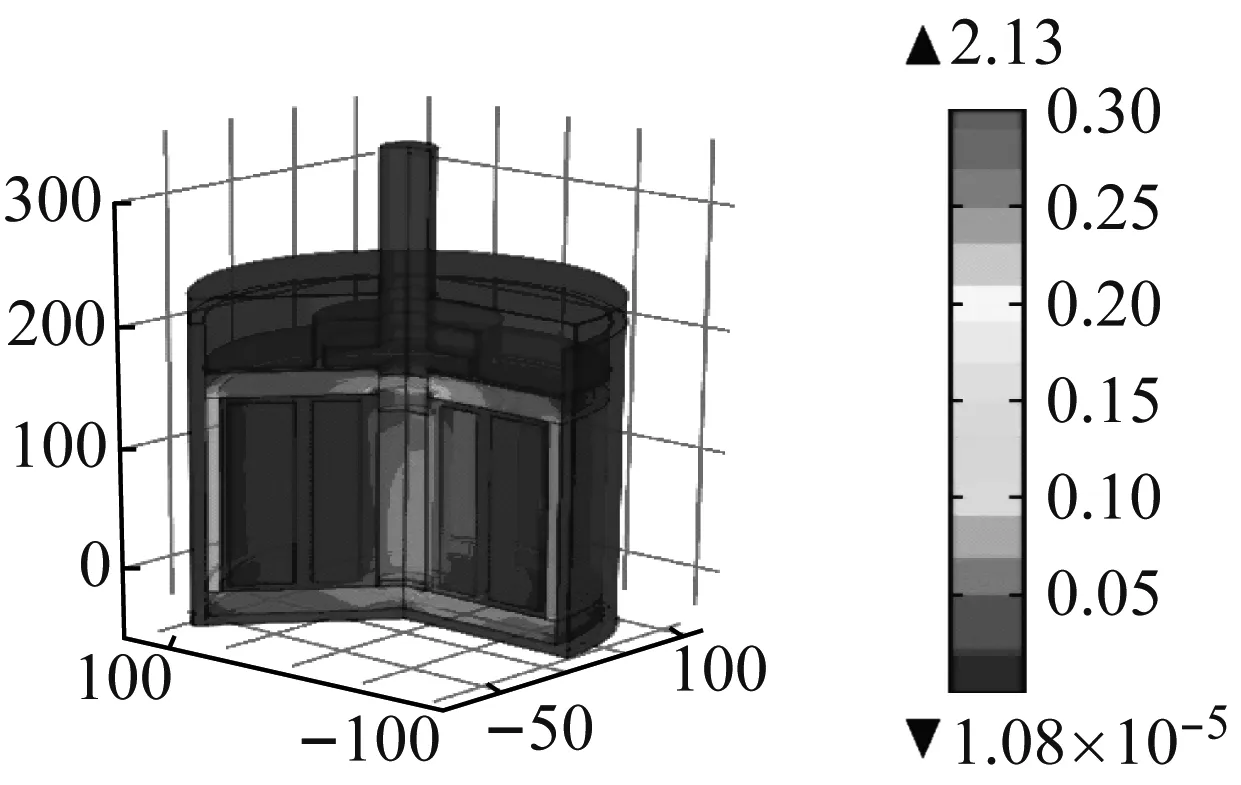
(b) 3D效果

图8为磁路结构闭合时磁棒轴向磁场与磁力线分布。由图8(a)可以看出，当磁路为闭合状态时，GMM棒所处磁场均匀性更好，磁感应强度更强；因为磁力线是按磁场密度划分，由图8(b)可知，当磁路闭合时，在GMM棒周围磁力线分布更密集。由此可见优化设计的闭合磁路具有较好的磁场特性。

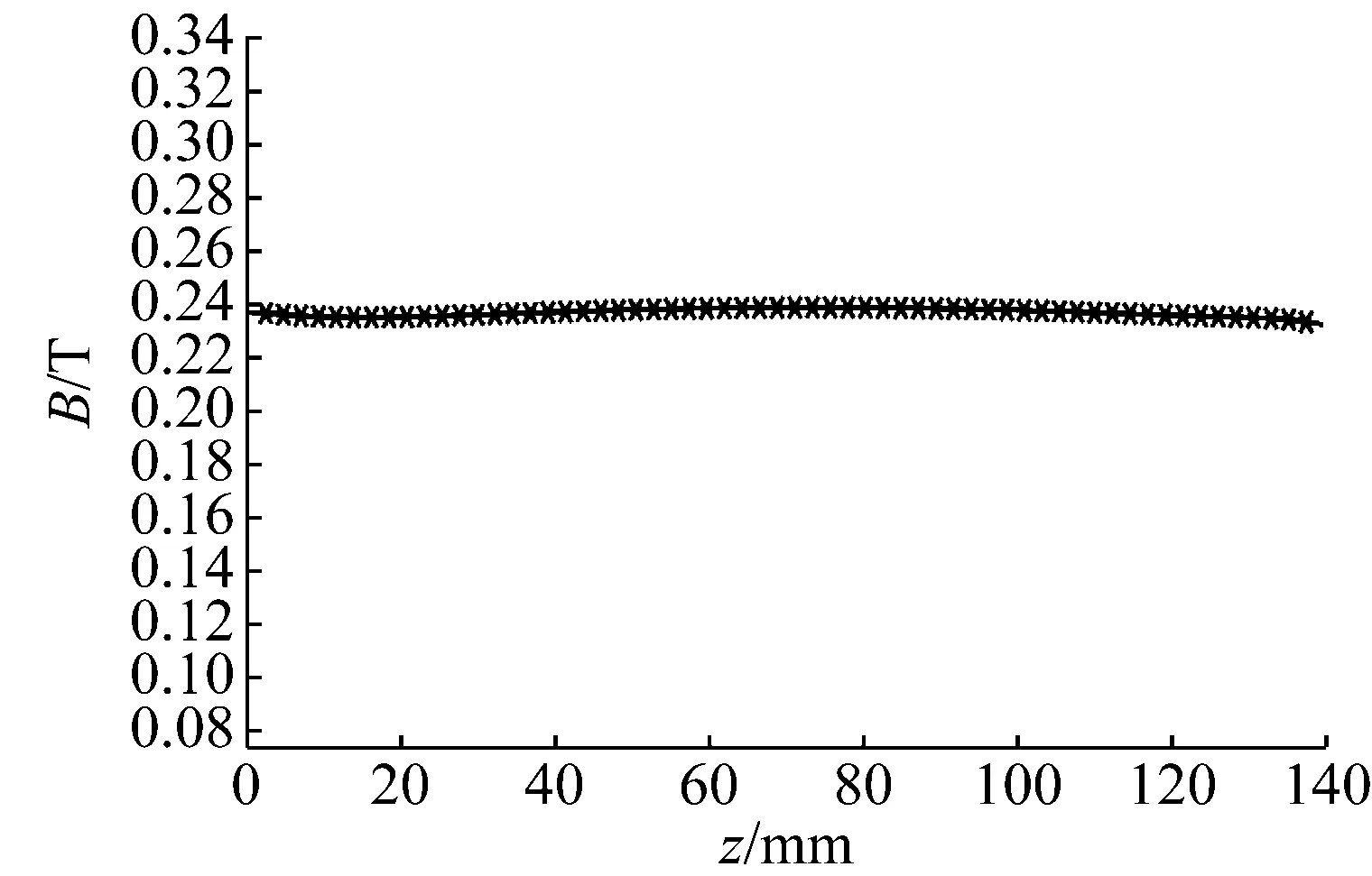
(a) GMM棒轴向磁场分布

(b) 磁力线分布

Fig.8 Axial magnetic field and magnetic lines distribution of bar magnet when the magnetic circuit structure is closed

3 激振器的数学模型与仿真

3.1 激振器的数学模型

激振器动态数学模型的建立是以超磁致伸缩激振器的电流为输入量，位移为输出量，其动态特性是输入电流激励下位移随时间变化的响应特性。图9为超磁致伸缩激振器的等效力学模型。

图9 超磁致激振器等效模型

建立激振器位移的数学模型前，先作如下假设：① GMM棒内的应力σ、磁场强度H、轴向应变ε均匀分布；② 碟簧具有足够快的响应速度，位移和应变完全满足线性关系，GMM棒、输出杆与碟簧具有相同的位移，且相位完全一致；③ GMM棒是轴向均质弹性杆，符合动力学理想模型；④ 空载时输出杆为负载，加载时负载为构件，均为质量-弹簧-阻尼负载模型[18]。

以此为前提，超磁致激振器即可简化为如图9所示的线性定常系统。

根据基尔霍夫电流电压定律

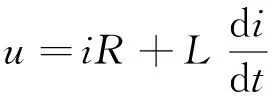
(8)

式中：u、i、L、R分别为驱动线圈的输入电压、电流、电感与总电阻；t为时间。RT为GMM棒的总磁阻，考虑等效磁路，Φ为激振器的总磁通

(9)

式中：x为激振器的输出位移；d33为GMM棒的轴向动态磁致伸缩系数。由于GMM棒的输出力F=Φ/d33，因此以激振器静平衡位置为位移的坐标原点，系统动力学方程为

(10)

式中:m1为GMM棒等效质量(均匀弹性元件在棒端的等效质量为棒质量的1/3)，m2为输出杆质量，k1、c1分别为GMM棒等效刚度系数和等效阻尼系数，k2、c2分别为碟簧刚度系数和阻尼系数，x为激振器输出位移，F为激振器输出力。将式(10)进行拉普拉斯变换，得到GMM棒输出力F到激振器输出位移x的传递函数，从而可推导出电流为输入，位移为输出的传递函数

(11)

式中：ωn为无阻尼固有频率；ξ为阻尼比。

3.2 激振器的的阶跃响应

由式(10)可知，超磁致伸缩激振器的动力学模型和质量m、阻尼系数c和刚度系数k等密切相关，这些参数对整个系统的动态性能有着不同程度的影响。GMM棒、输出杆和碟簧等材料的具体型号选定后，其力学性能相关的参数便可确定。因此，驱动线圈匝数直接影响系统的动态响应特性。在综合考虑超磁致伸缩激振器的输出力、输出位移，满足加速度要求的前提下，对GMM棒的驱动线圈进行优化设计。为了比较优化前后系统动态性能，把表1超磁致伸缩激振器的结构参数代入动力学模型，得到系统的传递函数，并在MATLAB环境下进行了仿真。图10是优化前后系统开环阶跃响应曲线。由图10可知，优化前，系统的响应时间为0.5 ms，优化后，响应时间为0.2 ms，响应速度明显加快。

表1 超磁致伸缩激振器的结构参数

图10 阶跃响应曲线

4 实验验证

4.1 激振器实验装置的组成

激振器实验装置如图11所示，主要由示波器、激振器、加速度传感器、可编程电源和计算机组成。计算机为整个实验装置的人机界面，由LabVIEW软件产生频率可变的脉冲信号，控制可编程电源输出方波功率脉冲，驱动激振器振动；示波器用于观察激振器的电流波形和加速度波形；加速度传感器把激振器输出的加速度变为电信号，经数据采集卡输入计算机；计算机记录不同频率下的加速度值，绘制阶跃响应曲线和幅频曲线，用优化前后的数值进行对比，以验证激振器的动态性能。

图11 激振器实验装置

4.2 实验数据分析

图12为实验测得的激振器的阶跃响应曲线。从图12可知，优化前，激振器阶跃响应的峰值时间为0.48 ms，超调量为17%，调节时间为0.66 ms。优化后，激振器阶跃响应的峰值时间为0.22 ms，超调量为21%，调节时间为0.41 ms。与优化前相比，优化后激振器响应速度明显提高。

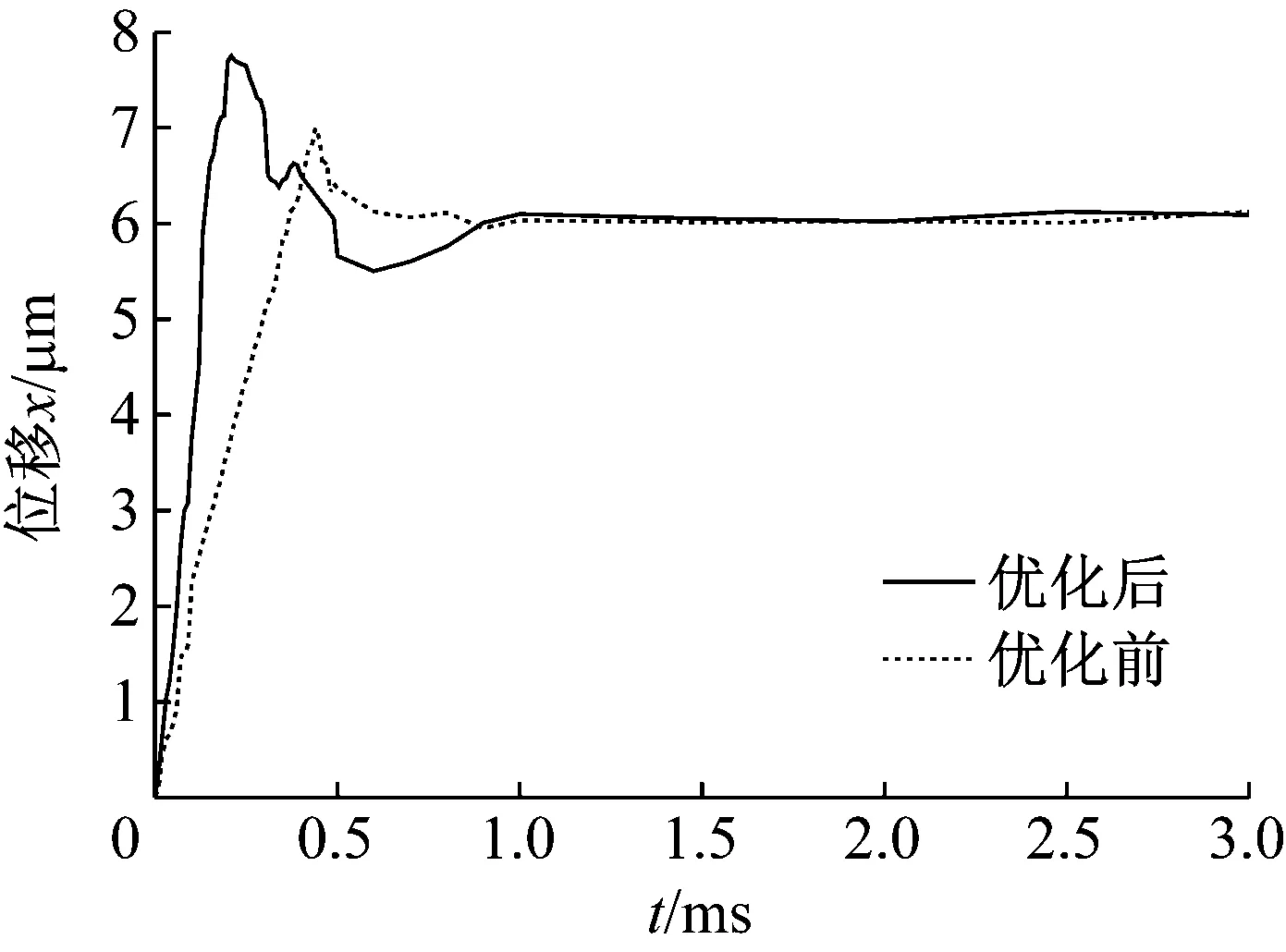
图12 激振器的阶跃响应曲线

图13为实验测得的激振器的幅频曲线。在幅频曲线中，频率范围均取1～1 000 Hz，由图13可知，优化前，幅值最大为-96 dB，最小为-171 dB，频率在1～220 Hz范围内时，幅值衰减尚不明显，但频率在220～1 000 Hz的范围内，幅值呈非常明显的下降趋势，仅在220～400 Hz，幅值就减小了9 dB，在整个频段内，幅值衰减很大。优化后，幅值最大为-88 dB，最小为-129 dB，频率在1～700 Hz范围内时，幅值仅减小了4 dB，幅值衰减不大，从700 Hz开始，幅值才开始较快下降，但总的来说，幅频曲线比较平坦，由此可见，与优化前相比，优化后的幅频曲线比较平滑，幅频特性大大提高。

图13 激振器的幅频曲线

在频率较高时，涡流损耗严重影响GMM的机电转换效率[19]，在频率较高时幅值出现很大衰减，GMM棒采用叠片式，可以大大降低涡流损耗，有效改善激振器的幅频特性。而减少驱动线圈的匝数，用方波电压驱动，可以显著改善激振器的阶跃响应。

4.3 振动时效应用效果

为了验证振动时效应用效果，对一构件实施振前扫频，其加速度峰值对应的频率为195 Hz，以此频率作为共振频率对构件进行振动时效处理，最后在相同的频带内实施振后扫频，采集振前扫频与振后扫频的加速度，绘制振动时效a-f曲线，如图14所示。由图14可知，振前扫频时，共振频率195 Hz处的加速度为38 m/s2，振后扫频时，共振频率变为115 Hz，该处的加速度为43 m/s2，显然，共振频率降低，加速度峰值升高。根据国家标准《振动时效工艺参数选择及效果评定方法》(GB/T 25712—2010)，比较振动时效a-f曲线的变化，振后扫频a-f曲线的加速度峰值较振前扫频升高，且共振频率较振前扫频降低，因此超磁致伸缩激振器达到了振动时效应用效果[20]。

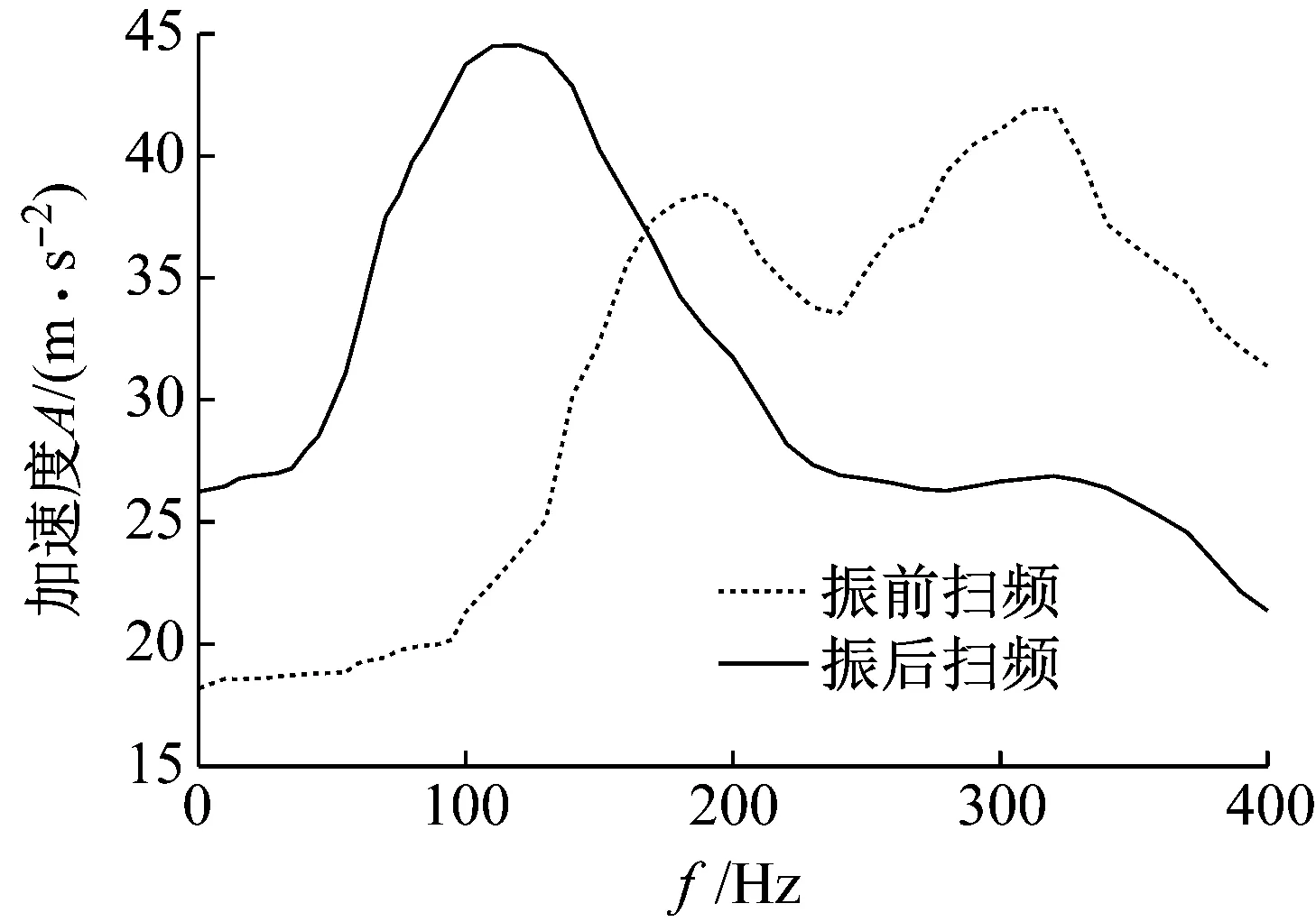
图14 振动时效a-f曲线

5 结 论

(1) 通过对超磁致伸缩激振器内部磁场进行有限元分析，优化设计的闭合磁路具有较好的磁场特性。

(2) GMM棒采用叠片式，可以大大降低涡流损耗，有效改善激振器的幅频特性。

(3) 采用减少匝数、增加线径、大电流驱动的设计方案，减小了驱动线圈的时间常数，显著提高了激振器的动态性能。

(4) 对比振动时效a-f曲线的变化，加速度峰值明显升高，共振频率大幅下降，超磁致伸缩激振器达到了振动时效应用效果。