不同应变率下岩-煤-岩组合体冲击动力试验研究

苗磊刚， 牛园园， 石必明

(1.安徽理工大学 能源与安全学院，安徽 淮南 232001；2.江苏建筑职业技术学院 能源与交通工程学院，江苏 徐州 221116；3.江苏省徐州技师学院 轨道交通学院，江苏 徐州 221151 )

冲击地压是影响煤矿安全高效生产的主要灾害类型，冲击地压的发生通常会引起煤岩体的剧烈破坏并释放出大量的能量，同时还可能会伴随着煤与瓦斯突出、瓦斯爆炸、瓦斯异常涌出、煤尘爆炸、水害和顶板冒落等次生灾害的出现。近年来，随着我国煤矿开采深度的不断延伸，煤矿开采在高地压、高地温、高应力等异常现象的影响下，冲击地压等煤岩动力灾害发生的频度和强度也逐渐增加[1]。据国家安全生产监督管理总局统计，2016年我国现有煤矿中有冲击地压危害的矿井的总数已超过160对，国有大型煤矿中，冲击矿压矿井有142座，开采深度超过1 000 m的矿井达到47座，冲击地压事故发生呈现不断增加的趋势[2]。因此，对地下工程中岩石动力学性能尤其是深部矿井中高地应力下煤岩组合体的力学行为进行研究有着重要的意义，此类研究可以为研究冲击地压发生的机理、防冲击地压工程的设计及施工提供有价值的技术参数和理论支持。

在国内对岩石，特别是煤岩的动态力学特性研究起步较晚，20世纪80年代之前研究少之又少，随着国内学者对岩石动力学特性研究的不断深入，逐渐取得一些研究成果。如单仁亮等[3-9]通过SHPB试验装置对单种岩石或者煤体的动力学特性、损伤模型、破坏机理、破裂模式、能量损失等内容进行了大量研究。刘少虹等[10-12]等对煤岩组合体进行单轴静态和少量的动态冲击压缩试验，研究煤岩体的力学性质、破坏规律和冲击地压发生的纪律。但是关于冲击作用下岩-煤-岩组合体的动力学特性、破碎特性和能量耗散规律等研究开展的较少。而煤矿冲击地压的发生，不单单是煤体或者岩体作用，而是煤—岩复合体的综合作用结果。因此对岩-煤-岩的动态力学特性研究，对研究爆破、冲击地压、地震、采掘等对煤岩体的影响有着重要的意义。因此，本文以岩-煤-岩组合体为研究对象，选取应变率、应力、应变、动态弹性模量和分形维数等为研究参数，对冲击荷载作用下岩-煤-岩组合体的动态力学特性进行研究分析。

1 试验概况

1.1 冲击试验技术及数据处理

岩-煤-岩组合体冲击作用下动态力学特性试验是在安徽理工大学能源与安全学院的冲击实验室SHPB试验装置上完成的，试验装置如图1、图2所示。该SHPB装置上的子弹、入射杆和透射杆的直径均为75 mm，材质为40Cr高强度合金钢，长度分别为0.4 m，4 m和2.5 m，弹性模量为195 GPa，密度为7 850 kg/m3,纵波速为4 985 m/s。应变片选用BX120-2AA型电阻应变计，采用DHHP-20超动态数据采集系统进行数据采集和处理。试验中将岩-煤-岩组合体试件正确安放，为了确保试件两端面与加载构件接触良好，在试件两端面涂抹适量黄油。利用粘贴在入射杆和透射杆上的半导体应变计采集3个脉冲信号(如图3所示)，即入射波εI、反射波εR和透射波εT，通过采集到三种应力波，利用三波法计算出岩-煤-岩组合体的应力应变(σ-ε)关系。

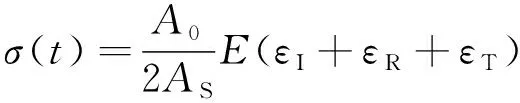
(1)

(2)

(3)

式中：AS为入射杆横截面积；A0为试件横截面积；C0为入射杆波速；Ls为入射杆长度；εI为入射波应变；εR为反射波应变；εT为透射波应变。

图1 霍普金森压杆实验设备

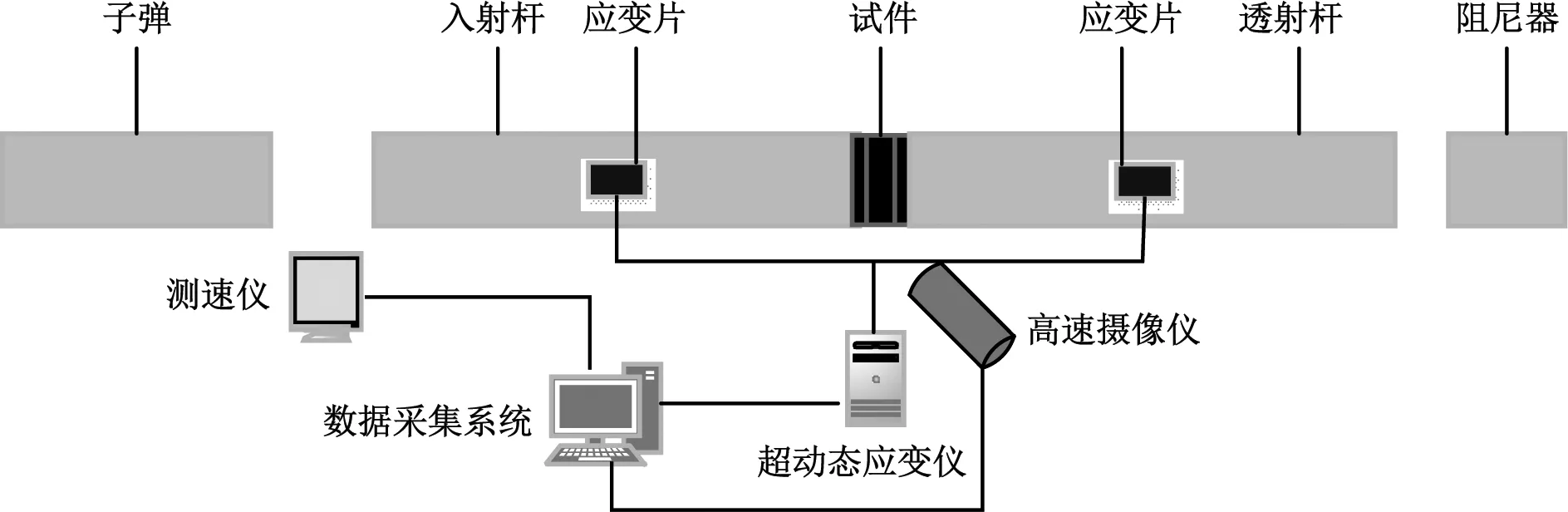
图2 实验装置系统示意图

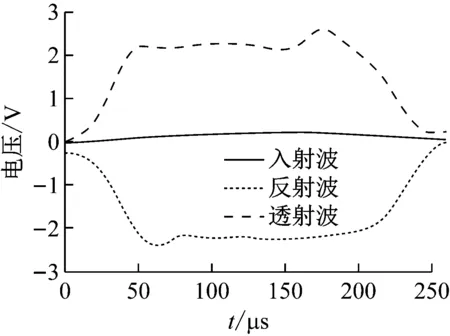
图3 典型波形曲线图

1.2 岩-煤-岩组合体试样制备

试验所用煤样取自淮南矿业集团张集煤矿13-1煤，所用岩石试样取自同一煤层的顶、底板岩石。煤层埋深约650 m，煤层结构简单，煤厚稳定，煤层平均厚度为4.4 m，煤质为气煤。13-1煤直接顶板岩石性质为砂质泥岩，老顶为中细砂岩；直接底板以泥岩为主，老底为砂质泥岩，采用了煤样和岩样1∶1的比例，与煤矿井下现场情况基本吻合，煤样工业分析参数如表1所示。试件制取在安徽理工大学能源与安全学院实验室内加工完成，所用煤、岩试件利用ZS-100型钻孔取样机分别从大块的煤、岩样中直接钻取，如图4所示；然后用DQ-4型切割机将煤样截取成高度相等的试件；再用SHM-200型双断面磨石机将每个试件断面都要认真仔细打磨，试件两端面的不平行度要小于规定值0.02 mm；岩-煤-岩组合体试件的两个端面应垂直于试件的轴线，最大误差不能超过规定值0.25°。试件的基本尺寸和加工精确度均应符合国家规定的岩石力学试验标准的要求，如图5所示。

表1 煤样工业分析参数表

图4 钻取岩芯

图5 试件制备

煤矿生产过程中，如图6所示为岩-煤-岩组合体的结构模型。根据SHPB试验的要求，为了使试件尽量减少惯性效应，满足试验均匀化假设，将组合体试件加工成直径50 mm，长径比在0.5～1之间的圆柱体[14]。因此煤岩组合体试件总高度设计为30 mm，其中每块煤和岩的厚度分别控制为10 mm，为了使煤岩组合体更接近现实情况，用环氧树脂胶将煤岩体进行黏结，保证其整个组合体试件的完整性、稳定性。对煤岩组合体进行编号,M代表煤样，Y代表岩样，YMY代表岩-煤-岩组合体，为了便于理解和更加形象，故称“三明治”结构，如图7所示。

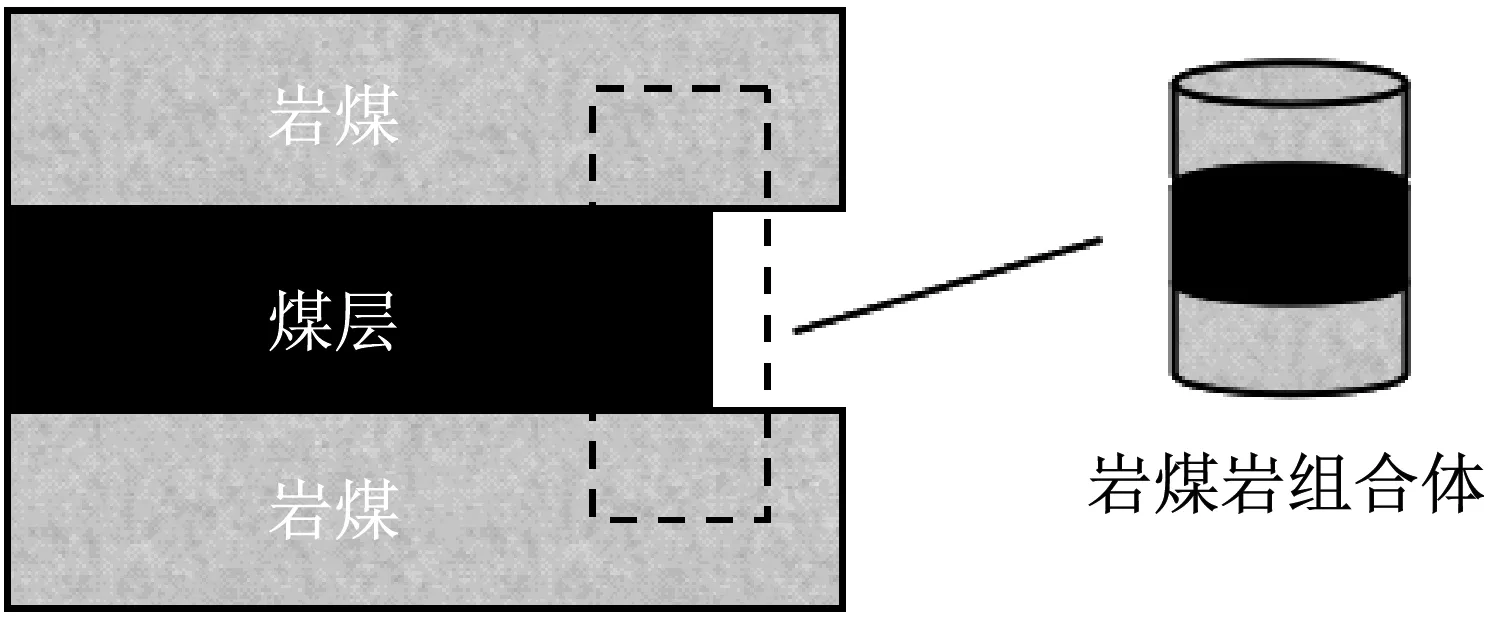
图6 岩-煤-岩组合体结构模型

图7 岩-煤-岩“三明治”结构

1.3 应变率的设定与分析

霍普金森压杆实验(SHPB)通过调节气缸压力，改变子弹撞击入射杆的速度来改变应变率的大小，从而得到不同应变率下组合体的动态力学特性。驱动压力越大，子弹速度就越快，撞击压力增大、加载的强度增强，试件的应变率也将升高。本次岩-煤-岩冲击实验，共分5种不同驱动压力进行试验，试件实验参数见表2。从表2中可以看出不同的气缸驱动压力下子弹的速度和应变率都会发生变化，随气缸压力的增大，子弹速度加快，应变率也相应增大。

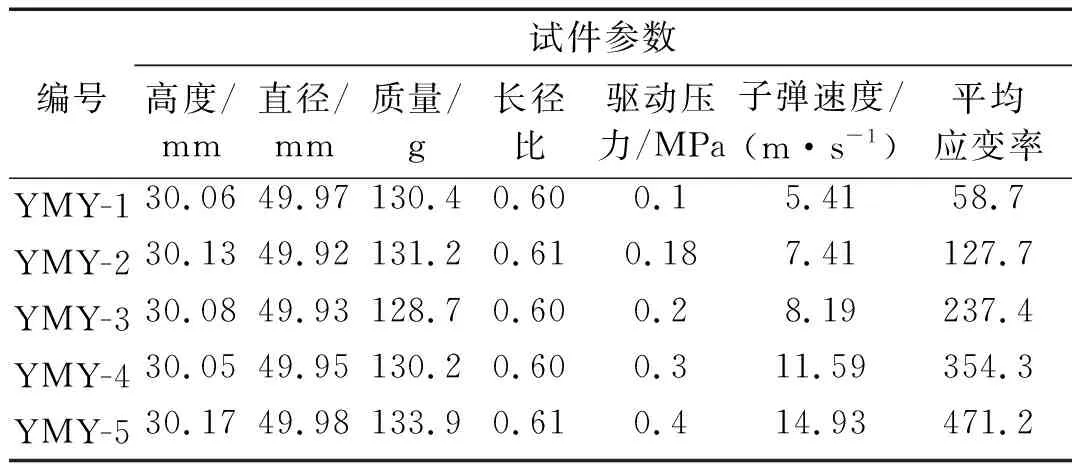
表2 试件试验参数

通过子弹对入射杆不同的冲击速度实现对岩-煤-岩在不同应变率的加载，岩-煤-岩试件在不同应变率情况下得到的应变率时程曲线，如图8所示，在子弹以不同冲击速度(v)下，岩-煤-岩试件均可以发现一平稳的应变率区间，取每条应变率曲线上升阶段的拐点到平稳阶段到下降阶段拐点这一区间的平均值作为平均应变率，即可以得到岩-煤-岩试件的近似平均恒应变率，计算结果见表2。

图8 应变率时程曲线

从图8中的应变率-时间的时程曲线可以发现，试件受到的子弹冲击加载速度越大，其应变变化的加速度就越快，平均应变率的峰值就越高，应变率到达峰值的时间就越短。应变率到达峰值后先有所下降然后再以较小加速度上升，这个阶段试件内应变开始应变强化，出现一段较为平稳的变化区间，最后出现跳崖式下降到0的现象，冲击速度越快，此阶段现象越明显。当试件受冲击后，25 μs内其应变率变化加速度较小，之后加速度迅速增加，恒应变率时长也也随着冲击速度的增加而增长，最后都以跳崖式的下降到0，不管应变率如何变化，最后都在约250 μs处交汇。从以上现象可以得出，岩-煤-岩组合体应变率峰值大小、应变率增加速度、试件内部应变强化高低、应变率达到峰值时间都与试件收到冲击加载速度有关系，说明岩-煤-岩组合体试具有很强的应变率相关性。

2 岩-煤-岩组合体动态力学性能分析

2.1 应力平衡分析

为了判断“岩-煤-岩”试样的真正受力状态达到了应力均匀化，现将对应变率为58.7 s-1试验工况下霍普金森杆试验进行平衡分析，如图所示9，图中包含入射波、反射波、透射波与比较波，其中比较波为入射波与反射波之和，从图9中可以发现应力平衡特性较好，可以判断试件受力达到均匀化，试验结果将有较高的可信度和准确度。

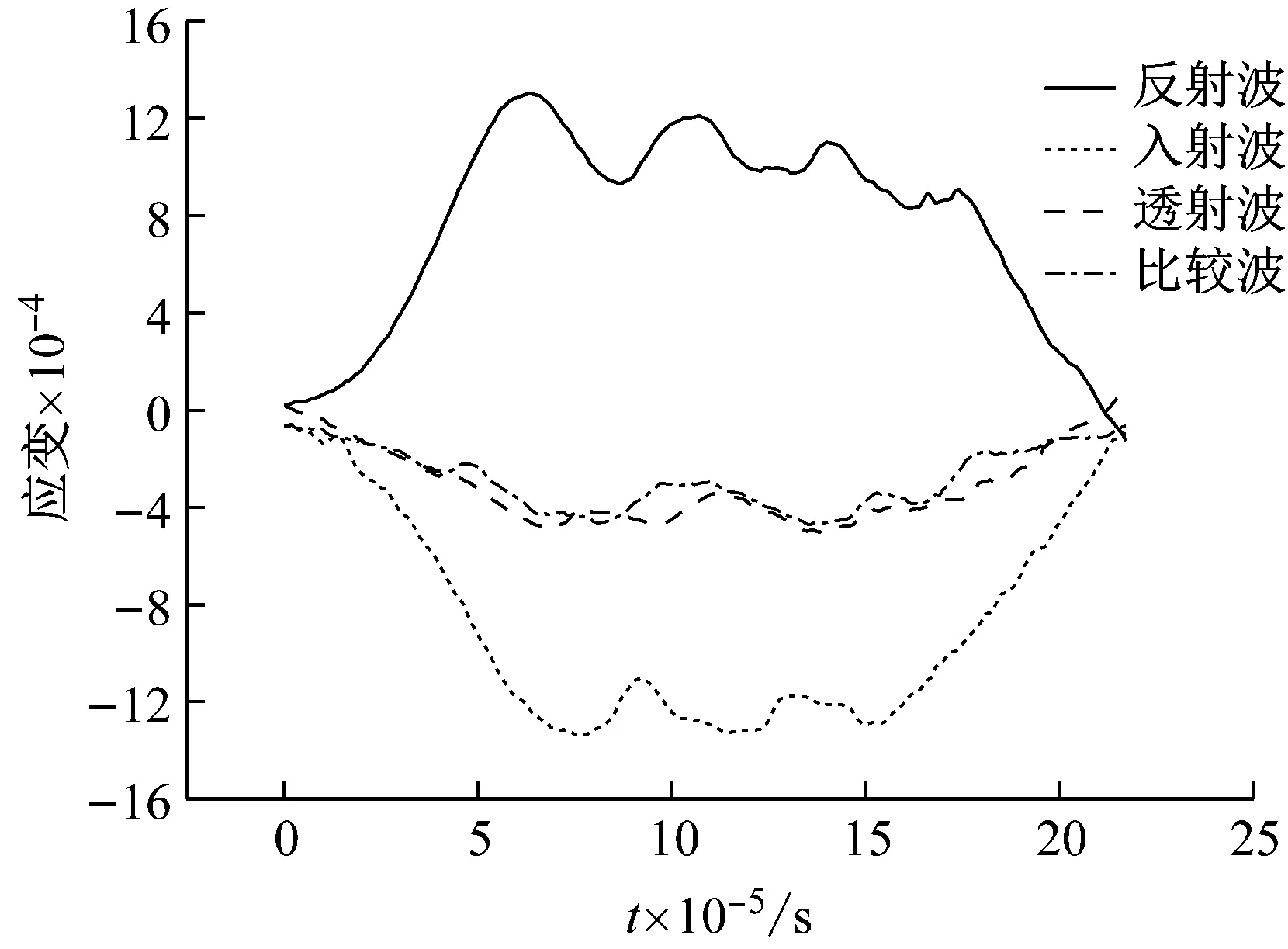
图9 入射波、反射波、透射波与比较波图像

2.2 不同应变率下应变时程曲线

从图10中可以发现，不同应变率下的应变时程曲线，在前20 μs之内，应变的变化差异性不大，变化较为缓慢，即使子弹的冲击速度变化很大，应变的变化也不明显。但在20 μs以后，随着子弹的冲击速度越快，应变率越大，应变变化的越明显，即应力波对应变有较明显的影响，应变率越高，曲线上升越迅速。现象表明岩-煤-岩组合体在受到外部冲击荷载时，开始初期阶段的变形具有弹性后效特性，但此现象会随着应变率的升高而加速减弱。

图10 不同应变率下应变时程曲线

2.3 不同应变率下应力时程曲线

从图11可知，岩-煤-岩组合体在不同应变率下的应力时程曲线具有一定的规律性，即应力跳跃式上升，和应变的变化趋势具有明显的差异性。应力到达峰值的速度，随着应变率的增加而加快。当应力到达峰值后，在高应力位置会持续约10 μs左右的时间，在煤岩组合体破碎失去承载能力后，应力迅速下降，其下降的幅度随应变率的增加而增大，其断崖式的下降现象趋于一致。

图11 不同应变率下的应力时程曲线

2.4 不同应变率下应力-应变曲线

从图12中可发现，随着应变率的变化，岩-煤-岩组合体的动态弹性模量也随之变化，动态弹性模量随着应变率的加大而不断增加；在应力-应变曲初始上升阶段具有一定的重合性。从微观结构来分析，由于煤岩本身存在的微小裂隙以及煤岩间的交界面，在初始受压后其应力-应变曲线先有一段向上弯曲，然后以直线式快速上升，当曲线上升到峰值应力的75%左右时，随着应力的增加，曲线斜率逐渐降低，试件的破裂程度逐渐发展，直至达到应力峰值。从整体来看，不同应变率下的σ-ε曲线达到最高值后，都会快速的下降，其下降的幅度与试件的破碎程度和应变率的大小都存在密切关系，但存在形态上的差异性。

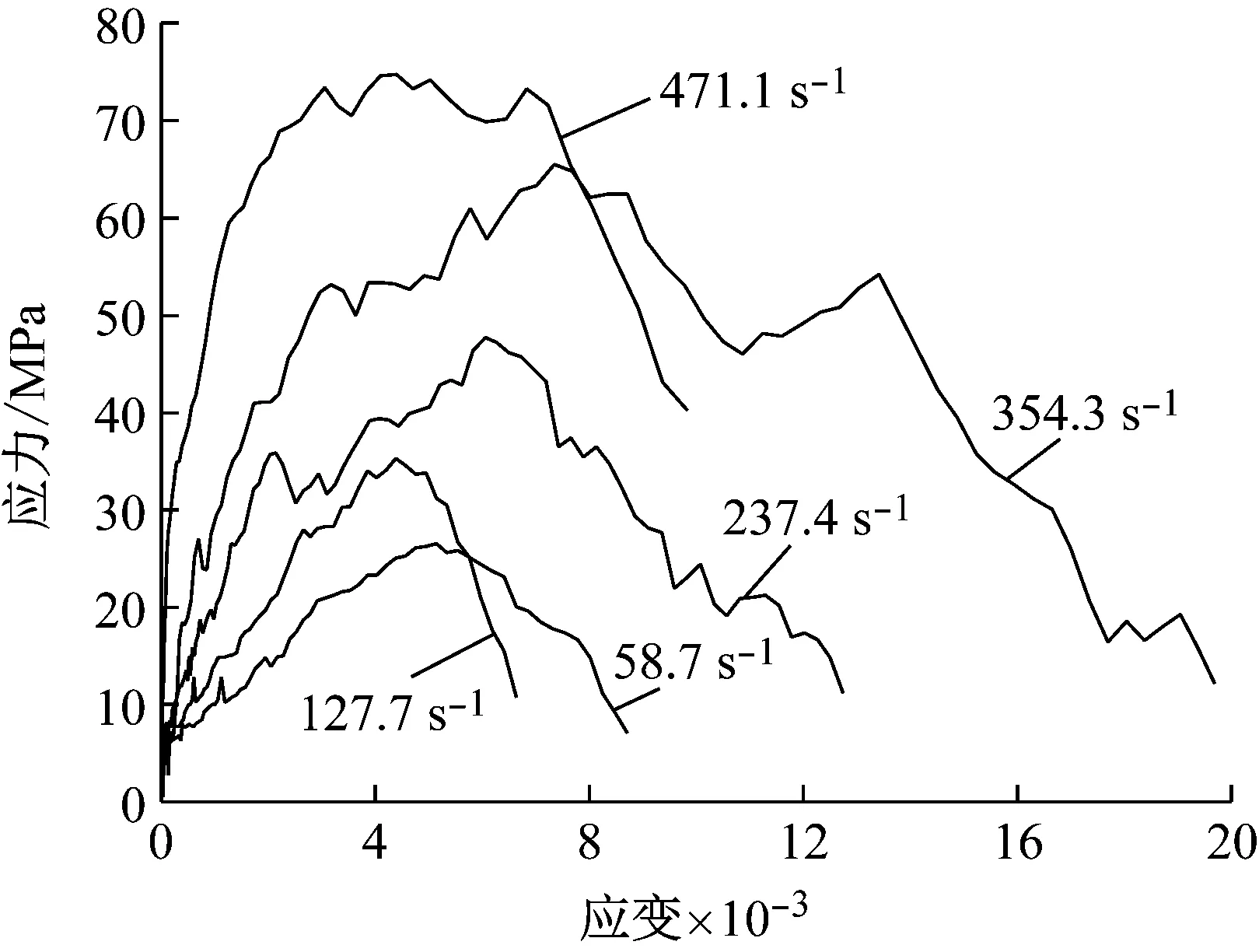
图12 不同应变率下的σ-ε曲线

3 不同应变率下的煤岩组合体动态破碎特性

3.1 应变率与破坏形态

岩-煤岩组合体本身内部具有微裂隙和交界面，组合体的破碎是冲击作用下裂隙发展的结果，煤岩组合体的受力状态可以通过其破坏的模式呈现出来，因此对岩-煤-岩组合体的破坏规律和模式分析研究是一重要环节。通过对岩-煤-岩组合体在冲击状态下的破坏形态进行观察，如图12所示，从组合体破碎形态来看，试件碎块的尺度随着应变率的增加而显著变小，碎块的数量增加明显，显现出了组合体破碎与应变率有很强的动态相关性。当冲击速度较小时，较低应变率下，如图12(a)所示，试件的破碎沿着加载方向轴向劈裂破坏，且具有明显的特征。当冲击速度较大时，岩-煤-岩组合体试件呈现压碎性破坏，且随着冲击速度的加快，破碎越严重，如图12(b)～(e)所示。

3.2 应变率与分维数

岩石破碎分形特性已被人们所接受，并在岩石爆破等领域块度分形理论中得到广泛应用[15]。利用碎块数量来估算分形比较困难，但是利用破碎后的各尺寸质量关系来计算更准确，岩石碎块质量——频率分布关系如式4所示[16-18]

(4)

将式(4)按级数展开，舍去高阶导数项，可得到M(R)/M=(R/R0)b，求导得dM∝Rb-1dR，由于碎块数目的增加必然会导致质量的增加，即dM∝R3dN，于是可以得到

Rb-1dR∝R3·R-D-1dR，

D=3-b

(5)

式中：M(R)为碎块直径小于R的质量，kg；M为碎块总质量，kg；R0为碎块平均粒径，mm；R为碎块粒径，mm；D为碎块的分维数。

(a)子弹冲击速度为5.41 m/s(平均应变率58.7 s-1)

(b) 子弹冲击速度为8.192 m/s(平均应变率127.7 s-1)

(c) 子弹冲击速度为14.931 m/s(平均应变率354.3 s-1)

图14为块度分布曲线，从图中可以发现岩-煤-岩组合体试件破裂后块度分布具有很好的自相似性。随着应变率的加大，冲击强度的增加，粒径小的碎块质量所占的比例不断增高，双对数坐标斜率也越来越小。

图14 不同应变率下岩-煤-岩冲击破碎块度分布曲线

根据分布曲线，得出岩-煤-岩组合体块度分维数，绘制出不同应变率下岩-煤-岩冲击破碎块度分维曲线，如图15所示。对比图13，图15得到伴随应变率的不断变大，组合体试件的破碎程度也在不断增强，破碎的块度体积变小，破碎块的数量显著变多，分维数值也不断增加。

图15 不同应变率下岩-煤-岩组合体分维数曲线

4 结 论

本文通过霍普金森压杆装置研究了岩-煤-岩组合体的动态压缩性能，得到动态冲击压缩下的应力-应变曲线，主要结论有：

(1) 岩-煤-岩组合体动态试验中，子弹冲击速度和应变率之间以及与组合体动态抗压强度都存在较好的线性关系，随着应变率的不断升高，组合体的动态弹性模量也不断增大。

(2) 组合体试件的变形具有弹性后效特性，但此现象会随着应变率的升高而加速减弱；试件所受应力到达峰值后，会在高应力位置持续约10 μs左右的时间，在煤岩组合体破碎失去承载能力后，应力迅速下降，其断崖式的下降现象趋于一致。

(3) 在试件受载初始阶段，σ-ε曲线以直线式快速上升，当曲线上升到峰值应力的75%左右时，随着应力的增加，曲线斜率逐渐降低，试件的破裂程度逐渐发展，直至达到应力峰值，持续短暂时间后迅速下降。

(4) 岩-煤-岩组合体在低应变率时呈现的是轴向劈裂破坏，当应变率较高时，岩-煤-岩组合体呈现是破碎性破坏，且随着应变率的变大，组合体破碎程度增强，块度体积变小，块度分维数值呈线性升高。