基于内表面特征的碗状碎块匹配方法

孙 进，丁 煜，习俊通，朱兴龙

（1.扬州大学机械工程学院，江苏 扬州 225100；2.上海交通大学机械系统与振动国家重点实验室，上海 200240）

1 引言

人类灿烂的文明和悠久的历史使得河流、湖泊、海洋下隐藏着众多的文化遗迹，其中以碗、瓶、罐、壶、盘等为器型的瓷器在水下文物研究中占有重要地位。备受瞩目的宋代沉船“南海Ⅰ号”近期结束清理工作，出水的十八多万件文物中以碗状器型存在的瓷器为多数[1]。这些水下文物在水底经过长时间的侵蚀和颠簸，大多数变得破碎残缺。随着信息技术的不断发展，利用计算机的虚拟复原技术来辅助文物碎块的实体拼合逐渐成为可能。为便于文物数字化表征，基于厚度值大致将破损物体分为两类：厚度小于1mm的如纸币、油画和地图等，称为碎片；厚度大于1mm的如碗、壁画和兵马俑等，称为碎块。考虑到水下文物中大部分是以碗状器型存在的物件，故以碗状碎块为研究对象。

传统的碎块匹配方法主要围绕断裂曲面展开研究。研究方向上大体可分为三类：第一类是基于碎块断裂曲面特征的重组匹配。文献[2]提出利用碎块表面的积分不变量刻画断裂曲面的弯曲能量，并采用向前搜索算法以及表面一致性约束完成碎块断裂曲面的匹配。文献[3]直接根据断裂曲面上所有顶点的三维坐标和曲率信息，采用基于随机采样算法和分级二叉树进行碎块的配对。目前，文献[4]提出了确定碎块匹配对的四个准则，即两个匹配碎块的间隙体积、碎块在匹配位置上的重叠性、两个接触面的平均曲率和接触弧的长度，该准则也得到了广泛应用。在此基础上，文献[5]先是根据断裂曲面的显著性区域实现碎块的粗匹配，然后通过加入高斯概率模型、角度约束和动态迭代系数的方式来改进ICP算法完成精匹配，提高了碎块匹配的正确率和对齐精度。但是断裂曲面的面特征信息过多，直接运算会造成算法的效率低下。一些专家学者受到碎片拼接方法[6-7]的启发，提出基于碎块轮廓曲线特征的重组匹配。文献[8]引进一种新的描述子表示碎块轮廓曲线上的特征点和曲线，然后使用快速傅里叶变换完成碎块的两两匹配，其中特征点的描述子是由曲率计算得到的，曲线的描述子用傅里叶级数表示。文献[9]针对碎块表面的特征轮廓线，提出了一种使用曲线矩的不变量和创建在碎块边界区域的锚点来实现碎块匹配和对齐的方法，并通过距离误差度量来估算特征轮廓线对齐的准确性。文献[10]识别出砂粒碎块特征曲线网络中所有简单的无弦周期，然后采用Hausdorff距离法和四点同余集算法对潜在的无弦周期进行匹配，从而完成对断裂砂粒碎块的重组匹配。又由于基于轮廓曲线的拼合方案被限定在碎块形状互补的理想条件下，任何几何外形上微小的缺失都会对算法产生很大的影响，基于自适应交互式的匹配方法应运而生。文献[11]提出一种基于自适应邻域的多特征融合文物碎块自动拼接方法，该方法基于自适应邻域机制融合碎块断裂面及原曲面上的多种特征，将断裂部位轮廓线的匹配转化为轮廓带的匹配，通过自适应邻域的匹配反馈碎块的匹配关系。

上述的碎块匹配算法比较单一，仅围绕断裂曲面的几何特征进行。倘若碎块的断裂曲面有部分几何特征遗失，那么容易在重组过程中产生错误的匹配；而且在曲面分割过程中，断裂曲面的“过分割”现象严重，需要研究者在提取断裂曲面特征前进行曲面合并，增加了重组算法的运行时间。相较于断裂曲面可能存在的问题，碗状碎块的内表面不仅具有和断裂曲面一样的几何信息，还拥有比断裂曲面更丰富的颜色信息和纹理信息，同时内表面的识别方法不需要对断裂曲面分割后产生的众多曲面进行合并，只需要正确区分出内表面即可，可以巧妙地避开过分割带来的问题。另外，当现有文献在讨论碎块匹配算法时，往往默认待匹配的一对碎块是可以拼接的，并没有展开碎块筛选方法的研究，而从碎块集中筛选出最佳匹配的一对碎块是计算机实现自动重组的必经之路。受碎片拼接算法[12]的启发，考虑到碎块的表面都是由复杂的曲面构成的，不同的曲面都具有自身的特殊性，这里将这些曲面的几何特征和颜色特征通过高斯映射在扩展高斯球[13]中表现出来。鉴于此，提出一种基于内表面特征的碗状碎块匹配方法，用于协助计算机自动筛选出两个最相似的待匹配碎块。

2 方法

2.1 碗状碎块的内表面提取

在一般的碎块模型中，主要存在两种类型的曲面：断裂曲面和非断裂曲面，通常可以根据曲面的粗糙程度[5]来识别断裂曲面。相比于非断裂曲面，断裂曲面上空间点的法向量变化程度更大，表面更凹凸不平。而对于碗状碎块的点云数据模型，采用区域生长算法[14]经过曲面分割后，如图1所示。可以将非断裂曲面细分为底面、原始表面、外表面和内表面四种类型，其中原始表面指的是区域生长算法在外表面和内表面交界处过度分割的曲面，这部分曲面表面积较小，仅存在外表面和内表面相邻的部分碗状碎块中。

图1 碗状碎块的曲面分类Fig.1 Surface Classification of Bowl-Shaped Broken Pieces

这里采用点云占比定性分析碗状碎块各分割曲面的性质，这主要是源于工程实践中的发现：相比于其他类型的碎块，碗状碎块的厚度较薄，导致其外表面和内表面的表面积要大于其他曲面，也造成外表面和内表面的点云占比明显大于其他曲面。点云占比可以描述碎块中各分割曲面的大小，一般采用曲面的空间点个数在碎块点云中所占的百分比来表示某一曲面的点云占比数值。通常根据各个曲面的点云占比，可以从碗状碎块的众多分割曲面中识别出外表面和内表面。

考虑到碗状物体在平时生活中的实际应用，外表面常用于抓取接触，内表面要便于清洗使用，而且一般情况下外表面还会设计一些凸出的纹饰特征，因此内表面一般比外表面更加光滑平整。数学表征为：相比于外表面，内表面上某一空间点的法向量与其周围点的法向量变化程度较小。为了便于定量表征，这里引入平滑度的概念。假设曲面S由n个点构成，即S={p1,p2,…,pn}，其中第i个点pi(1 ≤i≤n)的邻域点为pj(1 ≤j≤k)，那么曲面S的平滑度ε可以表示为：

式中：φi,j—pi的法向量与其邻域点pj的法向量的夹角。

ε的大小可以定量地反映曲面S的平滑度，曲面中相邻点之间的法向量变化愈小，则说明曲面的平滑度愈大，因此碗状碎块内表面的平滑度数值要大于外表面的平滑度数值，这样基于点云占比和平滑度能从碗状碎块的众多分割曲面中识别出内表面。接着采用KD树[15]建立内表面上各空间点的位置关系，然后进行K邻域搜索并求出各点的法向量和曲率，最后依据这些信息进行内表面边缘点的检测和提取。

2.2 碗状碎块内表面的特征提取

2.2.1 内表面边缘点的特征圆曲率计算

内表面边缘点所构成的轮廓线可以被看成是由一系列凹凸的平滑曲线组成，这些曲线凹凸部分的形状类似抛物线。对于一段类抛物线，采用弧长、短边与特征圆半径之比、长边与特征圆半径之比和弦长与特征圆半径之比来进行描述。P1、P2和P3均为碎块内表面的边缘点，P1P3的弧长用s表示，O是由P1、P2和P3确定的特征圆的圆心，该特征圆的半径用r表示，如图2所示。类抛物线的几何描述符可以表示为(s，a，b，c)，其中a表示长边与特征圆半径之比即a=| |P2P1/r，b表示短边与特征圆半径之比即b=|P2P3|/r，c表示弦长与特征圆半径之比即c=|P1P3|/r。

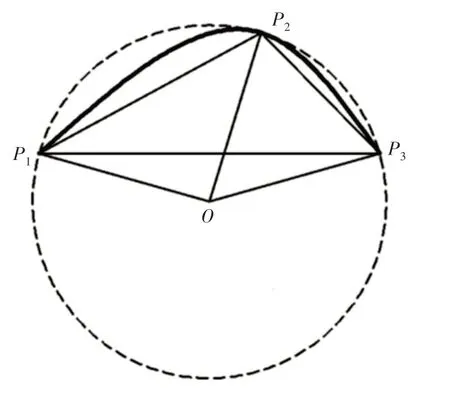
图2 类抛物线模型Fig.2 Likeness Parabolic Model

在类抛物线模型中，根据圆周角定理、扇形弧长公式和余弦定理可以计算出特征圆半径r，又因为特征圆曲率在数值上等于r的倒数，则内表面上第n个边缘点的特征圆曲率gn可以表示为：

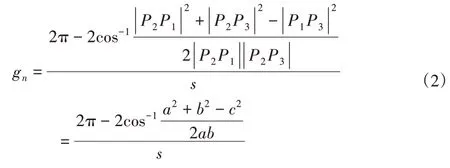
2.2.2 改进后的扩展高斯球

曲线和曲面的几何特征可通过高斯映射[16]来表示。高斯映射是将曲线或曲面上所有点的法矢先进行单位化，并将法矢的起点平移至同一个端点上，则曲线的各法矢端点落在半径为1 的单位圆上，曲面的各法矢端点落在单位球面上。法矢端点在圆上的投影点所构成的图像即为高斯图，在球上的投影点所构成的图像即为高斯球。传统扩展高斯球[17]的建立依赖于法向量和曲率，只能表征曲面的几何特征，这里为同时表征碗状碎块内表面的颜色特征和几何特征，改进扩展高斯球的建立方法。

首先单位化内表面边缘点的颜色矢量。为了让内表面边缘点的颜色矢量能均匀分布在各个卦限内，将RGB颜色空间模型的重心平移至坐标系的原点，如图3所示。那么单位化后的边缘点颜色矢量γn可表示为：

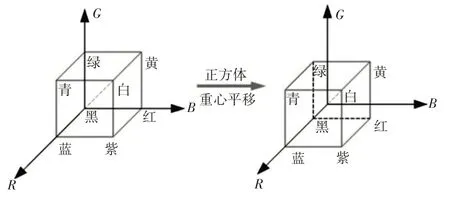
图3 RGB颜色空间模型Fig.3 RGB Color Space Model

式中：x=r-255/2，y=g-255/2，z=b-255/2，且(r，g，b)—内表面边缘点的RGB 颜色值；ε，μ和φ—x轴，y轴和z轴上的单位向量。

然后附加特征圆曲率信息。将单位化后的颜色矢量起点平移至原点，则其端点落在高斯球的球面上，再将特征圆曲率信息附加至高斯球的端点便形成扩展高斯球。改进后的扩展高斯球，边缘点颜色矢量的起点落在扩展高斯球的球心上，端点落在球面上，每个颜色矢量都带有该点的特征圆曲率。

2.3 基于相似度的碗状碎块筛选

建立扩展高斯球的目的是为了寻找两块相似的待匹配碎块之间的对应点，由于碎块内表面轮廓曲线的扩展高斯球都是在球坐标系下，所以使寻找对应点成为可能。相似的两块待匹配碎块之间由于RGB颜色特征和特征圆曲率的计算方法相同，其扩展高斯球上必有一部分形状相似。在球坐标系下，计算碎块内表面边缘点的颜色矢量与平面XOY的夹角，并按照夹角的大小沿着球半径将扩展高斯球平均分割成q个空间区域，令gM()为碎块内表面轮廓曲线M在第x个空间区域qx内第i个边缘点的特征圆曲率，其中i=1，2，…，m，同样令gN()为碎块内表面轮廓曲线N在第x个空间区域qx内第j个边缘点的特征圆曲率，其中j=1，2，…，n，若将M和N在空间区域qx内具有相同特征圆曲率的边缘点个数记为f(qx)，则f(qx)可用如下公式表示：

式中：gM(qx)，gN(qx)—M和N在第x个空间区域qx内的边缘点个数；q—沿着球半径将扩展高斯球分割得到的空间区域数量。相似度的数值越大，则代表两块待匹配的碗状碎块越相似。

2.4 匹配策略

结合基于内表面轮廓特征的粗匹配方法和基于ICP算法的精匹配方法[5]，提出一种基于内表面特征的碗状碎块重组策略，如图4所示。

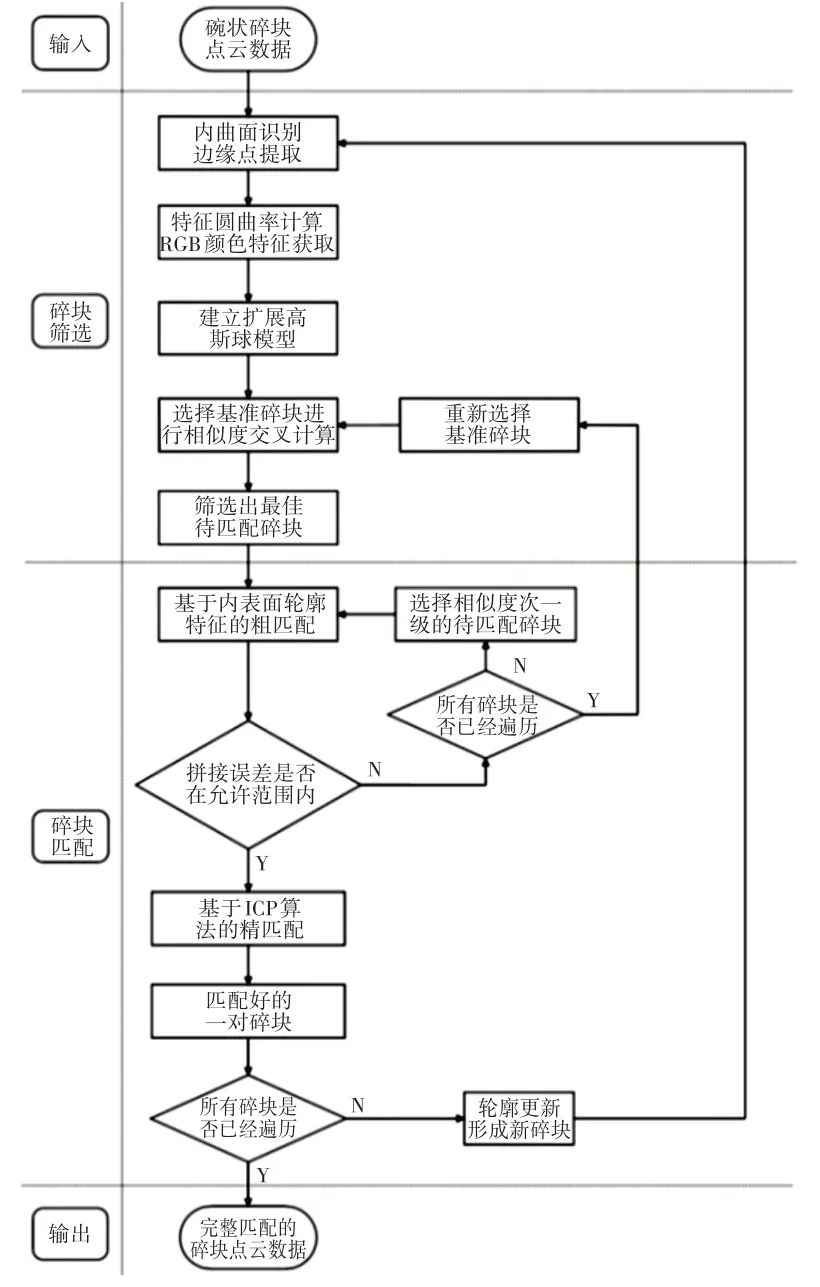
图4 碗状碎块的整体匹配策略Fig.4 Whole Reassembly Strategy of Bowl-Shaped Broken Pieces

具体方法步骤如下：

（1）将待匹配的碎块分别标记为block1,block2,…,blockn，状态设置为未访问，然后提取这些未访问碎块的内表面及其轮廓曲线，以碎块blocki(1 ≤i≤n)为基准模型，计算其他碎块内表面轮廓曲线与碎块blocki内表面轮廓曲线的相似度；

（3）若拼接误差在允许范围内，则选择ICP算法完成精匹配，并将碎块blocki的状态设置为已访问，然后将更新轮廓后的碎块设置为基准，回到（1）继续计算相似度；若拼接误差不在允许范围内，则回到（2），选择s值第二大的碎块与基准碎块进行拼接，直至拼接误差在允许范围内；若拼接误差始终不在允许范围内，则将碎块blocki剔除出待匹配的碎块集合，重新选择基准碎块进行拼接；

（4）每次精匹配结束后更新碎块的轮廓，直至完成碎块的整体拼合，待所有碎块均标记为已访问状态时，拼接结束。

3 实验

3.1 实验结果

实验的软件架构为Visual Studio 2010，VTK 5.8.0（Visualization Toolkit，视觉化工具函式库）和PCL1.7.2（Point Cloud Library，点云库），实验在Intel Core i3-4160 CPU@3.60Hz 处理器，4.0GB内存的PC上运行。碗状碎块的三维点云数据由Einscan-S三维激光扫描仪采集，首先建立碗状碎块的扩展高斯球模型，如图5所示。高斯球上点的矢量方向代表了边缘点的颜色特征，扩展高斯球上点的向量模代表了边缘点的特征圆曲率，此时扩展高斯球能完整地表征出碗状碎块内表面的几何特征和颜色特征。

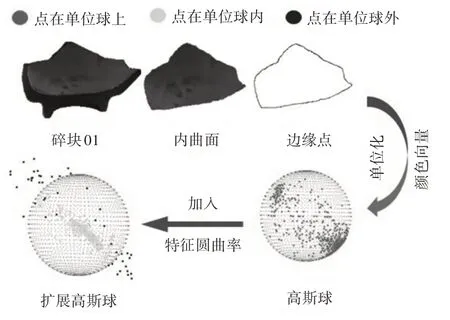
图5 扩展高斯球的建立过程Fig.5 Establishment Process of the Extended Gauss Sphere

接着本实验将碎块01作为基准碎块，剩余的碎块作为待匹配碎块，进行相似度的交叉计算，如图6所示。相似度计算结果表明与碎块01最相似的是碎块10。根据2.4节中所提出的匹配策略，对筛选出碎块01和碎块10进行拼接匹配。在一对碎块的重组完成后进行轮廓更新，筛选出下一个最佳待匹配碎块，然后进行下一步的拼接匹配，最后直至完成碎块集中所有碗状碎块的整体拼合。

3.2 实验讨论

传统的扩展高斯球模型建立方法依赖于点云的法向量和曲率值[16-18]，对于几何特征明显的碗状碎块可以很好地筛选出最佳待匹配碎块。但是对于区域相对平坦的碗状碎块，单纯依靠几何特征的方法容易产生错误筛选。如图7所示，传统的扩展高斯球建立方法在最佳待匹配模型的筛选过程中存在明显的错误。碗状碎块集B中碎块01的最佳待匹配碎块应为碎块02，而相似度计算结果却表明碎块01的最佳待匹配碎块是碎块06。在同样的情况下，如图8所示。基于RGB颜色特征和特征圆曲率的扩展高斯球模型建立方法，可以正确地完成碎块01的最佳待匹配碎块的筛选。

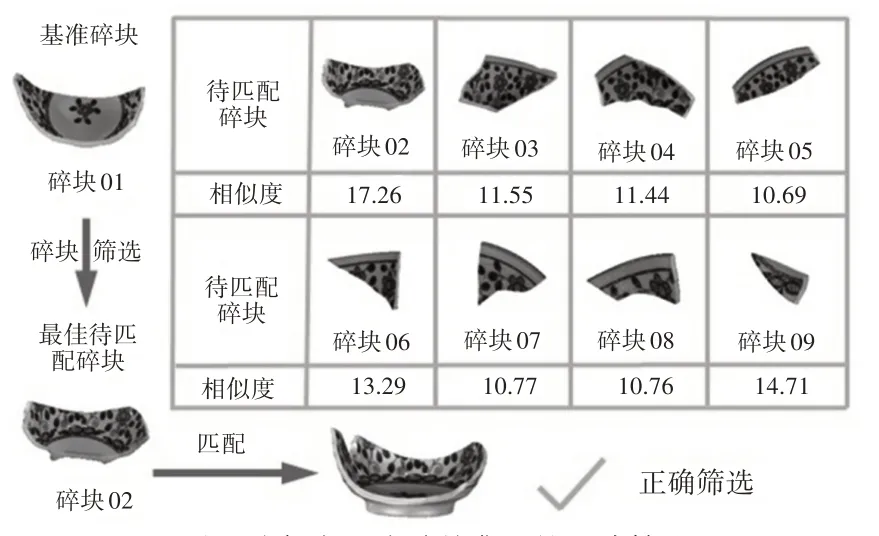
图8 我们方法在碎块集B的正确筛选Fig.8 Correct Screening Result in Broken Pieces Set B with Our Method

为了进一步验证以RGB颜色特征与特征圆曲率为基础建立的扩展高斯球模型更适合于最佳待匹配碎块的筛选，分别使用我们方法（即RGB颜色特征与特征圆曲率相结合的方法），初始方法（即HSV颜色特征与曲率相结合的方法）和传统方法（即法向量与曲率相结合的方法[16-18]）对碎块集A（图6所示的碎块）和碎块集B（图7和图8所示的碎块）进行重组匹配。如表1所示，相似度计算结果包括筛选准确率和算法运行时间。计算结果表明结合RGB颜色特征与特征圆曲率建立扩展高斯球模型来进行最佳待匹配碎块的筛选，碎块筛选的平均准确率可达到93.87%。与初始方法相比，我们方法的计算准确率比其高5.78%，平均运算速度提高了20.64%；与传统方法相比，我们方法的计算准确率比其高6.60%，平均运算速度提高了16.08%。因此基于RGB 颜色特征与特征圆曲率建立扩展高斯球模型的方法更适合于碗状碎块最佳待匹配碎块的筛选，在不同碗状碎块数据上的实验表明，该方法相比于其他扩展高斯球模型的建立方法更加优越。

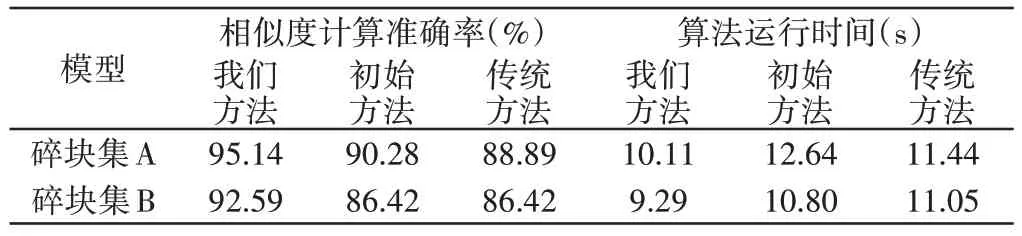
表1 相似度交叉计算结果的比较Tab.1 Comparison of Similarity Calculation Result

4 结束语

传统的碎块匹配方法通过研究断裂曲面的几何性质来达到目的，容易在曲面分割时产生过分割现象，从而增加了拼接过程的时间，为了避免这一情况，这里结合点云占比和平滑度提取碗状碎块的内表面，并将碗状碎块的内表面作为研究对象。此外，为了帮助计算机自动识别两个最相似的待匹配碎块，建立扩展高斯球模型将碎块内表面边缘点的几何特征和颜色特征融合起来，并通过构造类抛物线模型描述内表面边缘点的几何特征，然后定义相似度度量函数来描述扩展高斯球模型的全局特征，最后选择相似度最大的一对碎块进行碎块匹配，从而完成对碗状碎块的整体拼合。

实验表明结合RGB颜色特征与特征圆曲率建立扩展高斯球模型来进行相似度计算，相似度的平均计算准确率可达到93.87%，相比于传统的扩展高斯球模型建立方法，结合RGB颜色特征与特征圆曲率的方法在相似度计算准确率和平均运算速度上分别提高了6.60%和16.08%。在接下来的工作中，研究者不会仅仅局限于提高碗状碎块的匹配准确率和拼接效率，将进一步展开对不同形状碎块的相似度计算方法和匹配策略的研究，从而为建立水下文物虚拟拼接复原的工程化体系框架作铺垫。