基于粒子群优化算法的软土场地Davidenkov模型参数拟合与应用

王沿朝， 陈清军

(同济大学 土木工程防灾国家重点实验室，上海 200092)

土的动力非线性本构模型是土动力学研究的重要课题之一，也是土层及土-地下结构相互作用非线性地震反应分析中必须要考虑的内容。土体是一种非线性很强的材料，在循环荷载作用下，其应力-应变关系主要表现出非线性、滞后性和变形累积的特性。研究表明，在地震动的作用下，土体几乎不存在线弹性阶段，且随着地震动强度的增大，其非线性程度亦越强[1]。因此，如何对土体在动荷载作用下的应力-应变关系进行正确描述一直是研究者们所关注的问题。

目前，对于土体动力非线性本构模的研究主要集中在以下三个方面[2-7]：①等效线性化方法；②真非线性动力本构模型；③时域滞回非线性分析方法。在这三种方法中，等效线性化方法形式简单直观，计算量少，但由于不能计算永久变形，在强震动时的计算结果误差大，且容易产生“虚共振”现象等缺点，因而也制约了其进一步的发展。真非线性动力本构模型虽然能够准确的对土体的动应力-应变关系进行描述，然而由于其模型参数较多，实现起来较为复杂，且通常很难通过常规试验获得，因此其应用范围也不是很广。时域滞回非线性分析方法兼有上述二者的优点[8]，比如Davidenkov模型，既能较好的对土体的非线性行为进行描述，同时其表达形式相对于真非线性动力本构模型更为简单，便于推广应用。

为探究Davidenkov模型在软土场地地震反应分析中的应用，本文将推导Davidenkov模型的非线性动力本构模型在初始加载、卸载和再加载阶段的增量剪切模量表达式，并将土体动应力-应变关系推广到三维。基于粒子群优化算法对Davidenkov模型的参数进行拟合，利用MATLAB编制拟合程序，通过典型砂土和黏土验证拟合效果。在此基础上，将利用ABAQUS软件提供的二次开发平台UMAT，编制基于Davidenkov模型的土体非线性动力本构模型计算子程序，利用复杂加载路径验证该子程序的正确性，实现在ABAQUS软件中软土非线性动力本构模型的二次开发，并通过对某典型上海软土场地的地震反应计算，对比分析上海软土场地基于非线性动力本构模型的计算结果和等效线性化结果间的差异。

1 Davidenkov模型表达式及其参数拟合

1.1 Davidenkov骨架曲线理论公式

Hardin等[9]提出，土体的应力-应变关系可以通过一种双曲线形式来描述，其动剪切模量比的表达式如下

G/Gmax=1-H(γ)

(1)

(2)

式中：G为剪切模量；Gmax为最大剪切模量；γ为剪应变幅；γref为参考剪应变，一般可取动剪切模量比为0.5时所对应的剪应变幅。

Martin等[10]采用Davidenkov骨架曲线来描述上述关系，将式(2)改写如下

(3)

式中：A，B和γ0均为和土性有关的拟合参数。此时，γ0已不再是具有明确物理意义的参考剪应变，而仅为一个拟合参数。由式(3)可知，当A=1.0，B=0.5，γ0=γref时，Davidenkov模型即退化成Mashing双曲线模型。

因此，Davidenkov模型的应力-应变关系的骨架曲线可用下式表示

τ(γ)=Gγ=Gmaxγ[1-H(γ)]

(4)

将式(3)代入到式(4)中，即可得到

(5)

由式(5)可以发现，当B<0.5时，若γ→ ∞，则τ(γ) → ∞，而这与土体实际的应力应变关系是不相符的。为此，参考文献[11]的研究方法，通过分段函数的形式来对Davidenkov模型的骨架曲线进行改进，即引入一个剪应变上限值γult，当土的剪应变γ超过γult时，便可认为该土体处于破坏状态，此时若γ继续增加，土体的剪应力τ也不再增加，甚至可能会减小。若不考虑软化效应，则骨架曲线可表示为

(6)

τult=Gmaxγult[1-H(γult)]

(7)

而根据曼辛准则，以Davidenkov骨架曲线为基础的土体应力-应变滞回曲线可表示为

(8)

式中：τc和γc分别表示的是应力-应变滞回曲线中加卸载转折点处的剪应力与剪应变幅值。

1.2 剪切模量的增量表达式

由于土体在外荷载作用下几乎不存在弹性阶段，因此可以将土体假定为理想的黏弹性体，进而，可以从一般的模量衰减曲线得到归一化的剪应力

(9)

对上式求γ的导数，即可得到

(10)

式中：Ms为归一化的割线模量，γ为剪应变，Mt为归一化的切线模量。则增量剪切模量G可以表示为

G=GmaxMt

(11)

对式(6)进行求导，即可得到Davidenkov骨架曲线中的增量剪切模量如下式

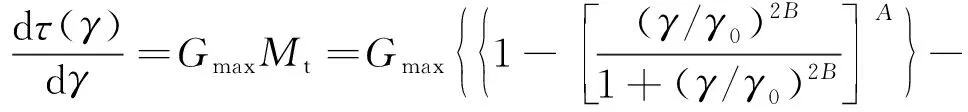
(|τ|≤τult)

(12)

对式(8)进行求导并令R=|γ-γc|/(2γ0)，则可得到卸载及再加载阶段的增量剪切模量如下式

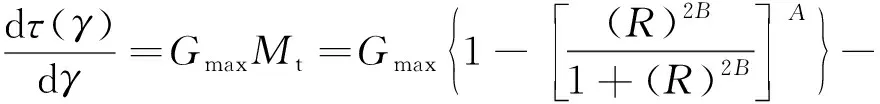
(|τ|≤τult)

(13)

而当|τ|>τult时，G=0。

由此，得到了基于Davidenkov骨架曲线及滞回曲线的完整的加载、卸载及再加载的增量剪切模量的表达形式。

1.3 基于粒子群优化算法的土体参数的拟合

当采用基于Davidenkov骨架曲线的非线性动力本构模型时，必须根据土体的动剪切模量与动剪应变试验曲线来对式(3)中的三个参数A、B、γ0进行拟合。参数拟合问题的本质是函数优化，目前已有一些解决方法，如牛顿法、遗传算法等。然而，当函数是超高维、多局部极值的复杂函数时，这些算法的效果并不理想。研究发现，对大多数的非线性函数，粒子群优化算法在精度和优化速度上均优于上述算法[12]。本节基于粒子群优化算法编写了相应的优化程序对Davidenkov模型的参数进行拟合。

粒子群优化算法是一种群体智能算法，由Eberhart等[13-14]发明，在标准粒子群优化算法中，每个优化问题的解被看成是搜索空间的一个“粒子”，假设在一个D维目标搜索空间中，有M个粒子组成一个群体，其中在第t次迭代时，粒子pi的位置矢量为xi(t)=(xi1,…xiD)，速度矢量vi(t)=(vi1,…,viD)。在每次迭代中，粒子都通过追踪两个极值来对自己的速度和位置进行更新。一个是个体极值点(粒子自身找到的最好解)，表示为pbesti=(pbesti1,…,pbestiD)；一个是全局极值点(整个种群当前找到的最优解)，表示为gbesti=(gbesti1,…,gbestiD)。在第t+1次迭代时，粒子pi根据式(14)和(15)来更新自己的速度和位置。

(14)

xid(t+1)=xid(t)+c3×vid(t+1)

(15)

式中:w为惯性权值；c1，c2为学习因子；c3为另一个惯性权值；rand1，rand2为两个[0，1]之间的随机数。

目前，常用来构建目标函数的方法包括互相关法、最小二乘法及基于信息熵的互信息法等。在本文中，目标函数衡量的是预测值与实际值差异的大小，目标值越大则拟合效果越好。因此，本文引入图像配准[15]中经常使用的归一化互相关法来构建目标函数，该方法通过计算互相关度量值NCC来确定试验数据与拟合结果的相似程度，其表达式如下

(16)

本文中粒子群优化算法具体的计算流程如图1所示。

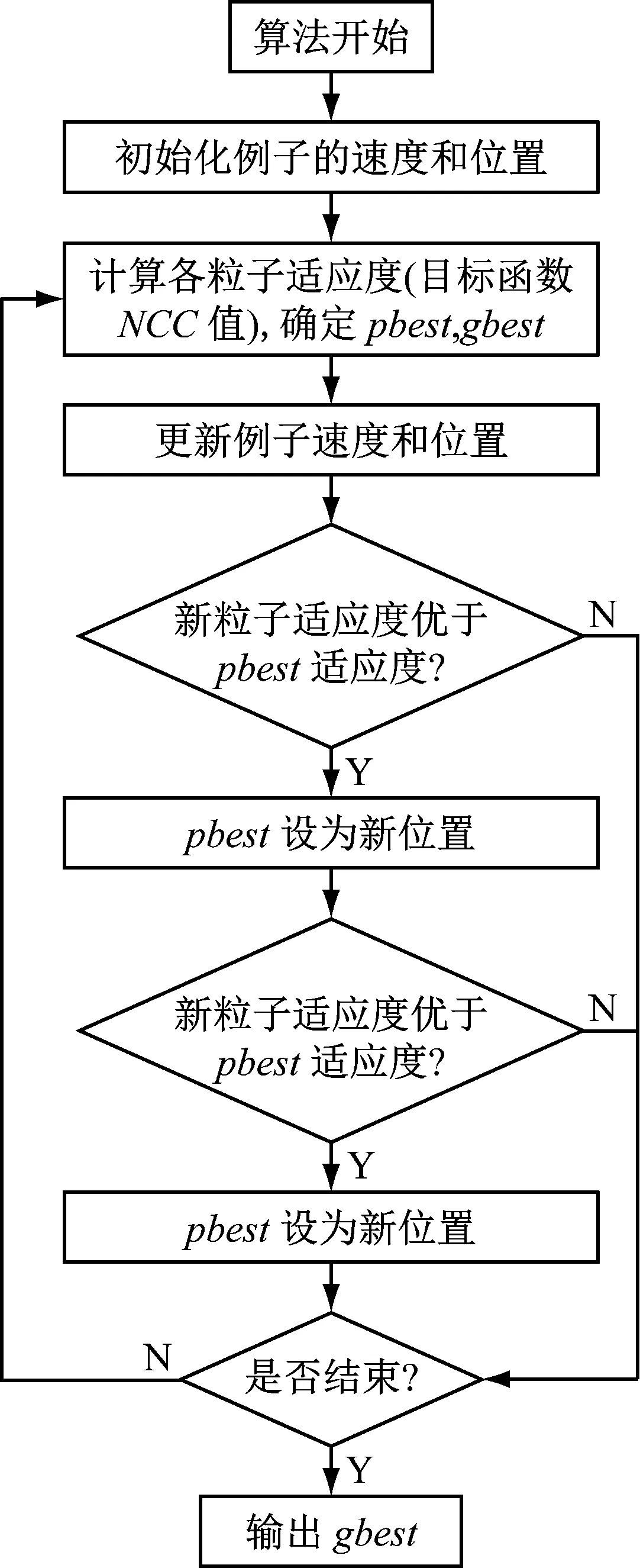
图1 粒子群优化算法流程图

基于以上理论，本文利用MATLAB编写了拟合程序。为了验证程序的可行性和正确性，首先对典型的砂土和黏土参数进行拟合，拟合中主要的参数变量为惯性权值w，加速因子c1，c2，种群数N，迭代次数M和粒子维数D。

(1) 种群规模。种群规模不能太大也不能太小，综合考虑算法的精度及效率，本次拟合选择种群规模为20。

(2) 最大迭代次数。迭代次数与解的收敛性成正比，但过大会影响运算速度，本文中选1 000次。

(3) 惯性权值。惯性权值w表征了粒子保留原来的速度的程度。w较大，全局收敛能力强；w较小，局部收敛能力强。本文选0.6。

(4) 加速因子。加速因子c1，c2分别用于控制粒子朝自身或邻域最佳位置运动。文献[16]建议φ=c1+c2≤4.0，并通常取c1=c2=2.0。本文也取c1=c2=2.0。

(5) 粒子维数。粒子维数即待优化函数的维数。

下面，通过粒子群优化算法对典型的砂土和黏土进行Davidenkov模型参数拟合，表1给出了Seed等[17]所给出的典型砂土和黏土的剪应变与剪切模量及阻尼比与剪应变幅的试验数据。在对模型参数进行拟合时，其他拟合参数不变，粒子维数取为3(3个参数需要拟合)。

表1 典型砂土和黏土剪切模量比和阻尼比试验数据

Tab.1 Shear modulus ratio and damping ratio of sand and clay

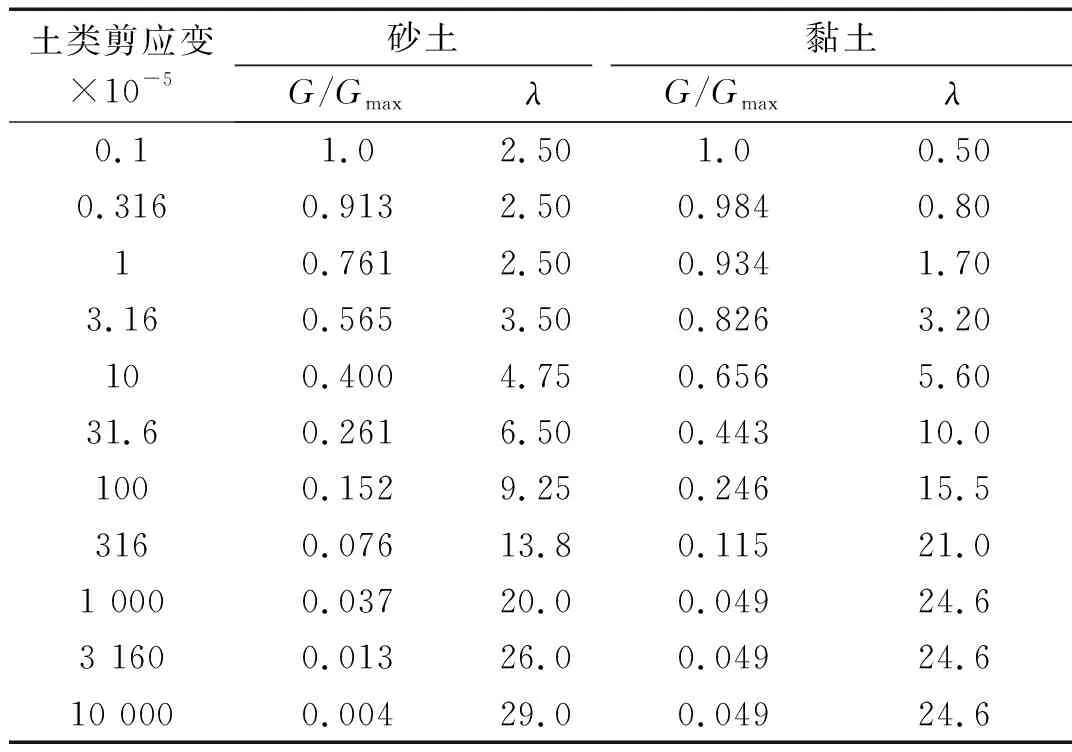
土类剪应变×10-5砂土黏土G/GmaxλG/Gmaxλ0.11.02.501.00.500.3160.9132.500.9840.8010.7612.500.9341.703.160.5653.500.8263.20100.4004.750.6565.6031.60.2616.500.44310.01000.1529.250.24615.53160.07613.80.11521.01 0000.03720.00.04924.63 1600.01326.00.04924.610 0000.00429.00.04924.6

典型砂土和黏土的拟合曲线如图2和图3所示，从图中可以看出，对试验数据拟合的曲线走势很好，Davidenkov模型参数拟合的结果及NCC值见表2所示，可以看出，两种土体拟合结果的NCC值均十分接近于1，说明了拟合效果很好。

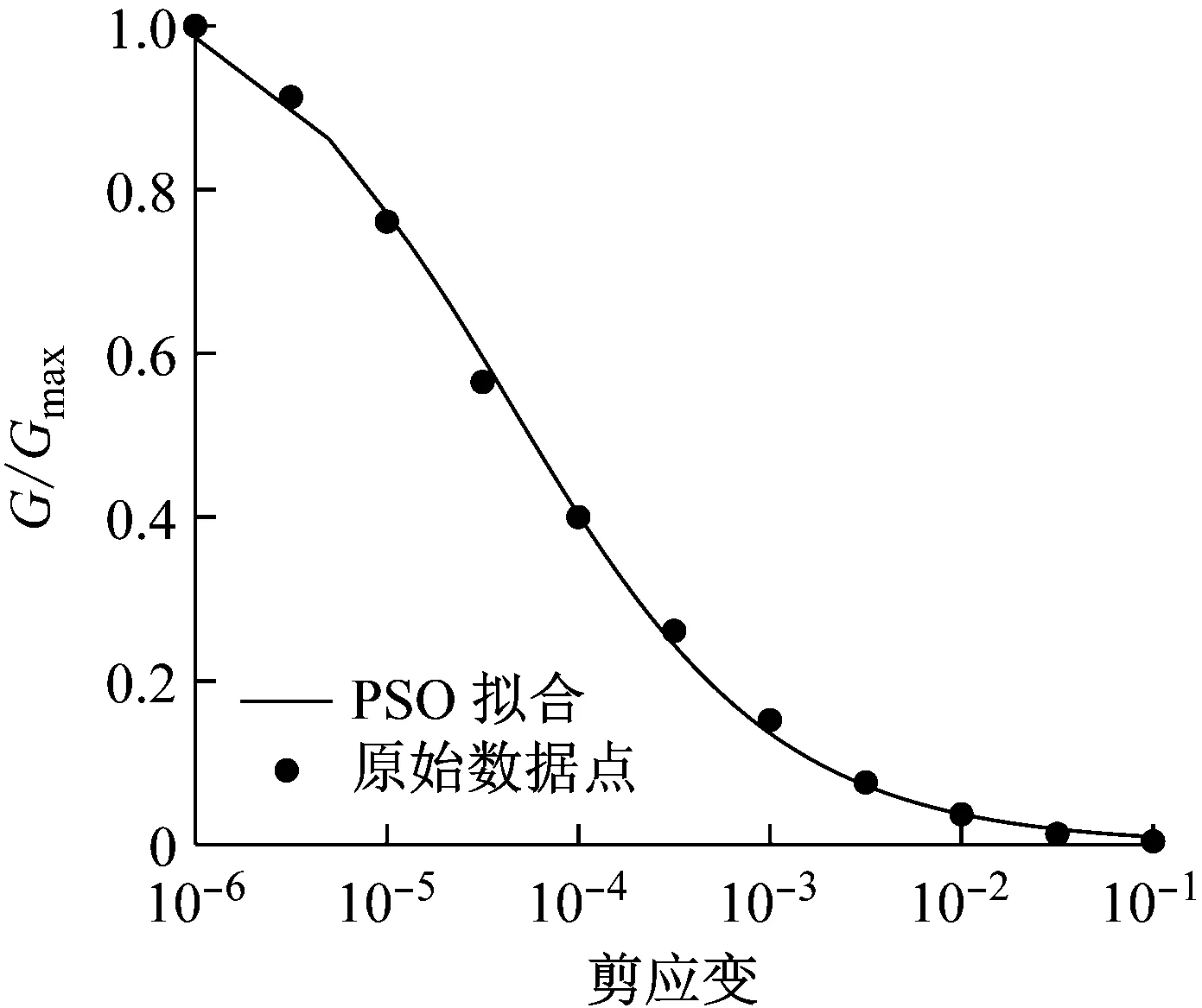
图2 砂土拟合曲线

图3 黏土拟合曲线

土类ABγ×10-4NCC砂土1.100.403.250.999 6黏土1.010.812.000.999 7

在此基础上，本文通过粒子群优化算法对典型上海软土进行Davidenkov模型参数拟合，表3给出了典型上海软土各层土的剪切模量比及阻尼比与剪应变幅的试验数据。对模型参数进行拟合时，其他拟合参数不变，粒子维数取为3。典型上海软土各层土的拟合曲线如图4所示，Davidenkov模型参数拟合的结果及NCC值如表4所示。

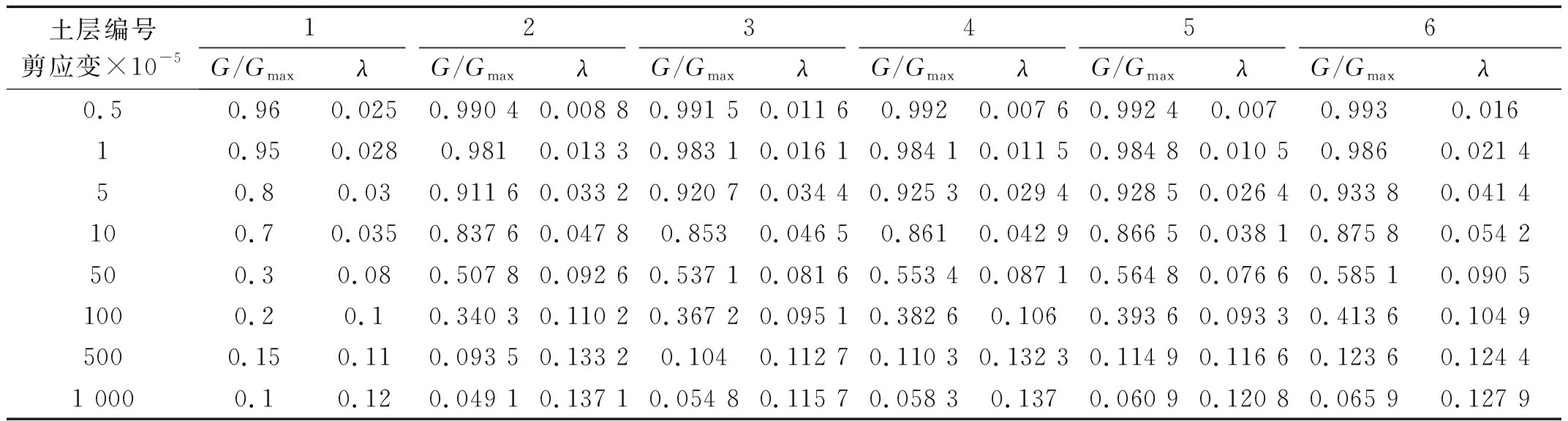
表3 典型上海软土各土层剪切模量比和阻尼比

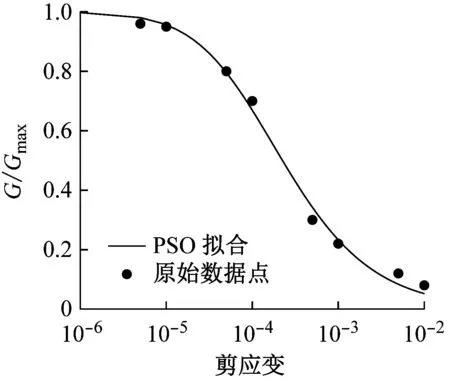
(a) 土1

(b) 土2

(c) 土3

(d) 土4

(e) 土5

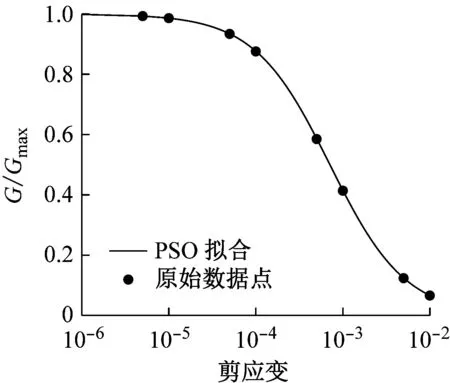
(f) 土6

图4 典型上海软土各层土拟合曲线

Fig.4 Fitting curves of typical Shanghai soft soils

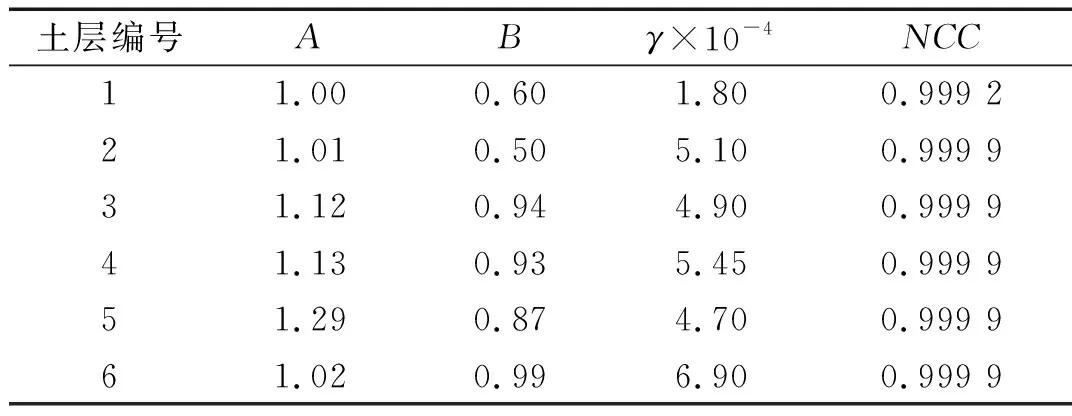
表4 典型上海软土拟合结果

2 Davidenkov模型在ABAQUS中的实现

2.1 实现过程

ABAQUS为用户提供了功能强大的用户子程序接口，以帮助用户开发基于ABAQUS内核的程序，而这其中应用最为广泛的子程序即为UMAT[18]，它主要用于用户开发自己的本构模型，以弥补ABAQUS自带材料模型的不足。ABAQUS子程序通过FORTRAN语言开发。按照FORTRAN的语法，用户可以自由的编辑代码，并形成一个独立的程序单元，该单元能被独立的编译和存储，也可以被其他单元引用，利用UMAT能够将大量的数据带回供引用程序使用。

UMAT的主要任务是根据ABAQUS主程序传入的应变增量更新应力增量和状态变量(如有必要)，并给出雅克比矩阵供ABAQUS求解使用，主程序结合当前荷载增量求解位移增量，继而进行平衡校核，如果不满足指定的误差，ABAQUS将进行迭代直到认为收敛，然后进行下一增量步的求解。因此，UMAT文件主要包含以下几个部分：

(1) 子程序定义语句；

(2) ABAQUS定义的参数说明；

(3) 用户定义的局部变量说明；

(4) 用户编制的程序主体；

(5) 子程序返回和结束语句。

对于本文来讲，ABAQUS的本构模型开发工作主要是修改用户定义的局部变量及程序主体的编制，通过定义材料参数数组来实现初始参数的输入，通过定义状态变量数组来存储与本构模型有关的参变量。对于程序主体，则按照骨架曲线和滞回曲线的加载、卸载及再加载的路径模式进行编制，来体现土体剪切模量的变化。

2.2 加卸载转折点的实现思路

对类似于岩土体的颗粒破碎材料，其一维与三维条件下的力学行为的差别是很大的。因此，在进行地下结构三维的非线性动力分析时，应当将前述的应力-应变关系从一维扩展至三维。

在程序编制过程中，如何确定加卸载转折点是一个关键的问题，对于三维问题，至少存在6个应变率张量分量[19]，即：

(17)

式中：Δeij为应变增量张量。

(18)

(19)

式中，vi表示各分量上的应变增量，下标i表示1～6个分量。

(20)

因此，可以判断，当d小于0时，应变发生转向。

在实际情况中，当土体单元的广义剪应力的绝对值大于土体的剪应力上限值τult时，土体的抗剪强度并不会完全丧失，其仍然具有一定的残余强度，因此，编程时可假定各类土破坏时的剪切模量Gmin=0.05Gmax。

按照弹性力学理论，应力-应变关系为

(21)

式中，λ是拉密常数，可通过下式求得

(22)

式中：ν为泊松比。

为了对土体的黏性效应加以考虑，本文按Rayleigh阻尼的概念定义黏性阻尼矩阵为

[C]=α0[M]+α1[K]

(23)

式中：α0，α1分别为与质量矩阵和刚度矩阵有关的Rayleigh阻尼系数。

由于振型对Rayleigh阻尼矩阵是正交的，因此可得

(24)

式中：ξi为第i振型阻尼比，对于典型上海软土，通常可取8%～10%；ωi为第i振型的自振频率。

本文参考文献[11]的研究成果，取第一振型作为计算Rayleigh尼系数的振型并假设阻尼矩阵只与刚度矩阵有关，则：

α0=0,α1=2ξi/ω1

(25)

因此，总应变速率产生的阻尼力为

(26)

式中：Del为初始弹性矩阵。

综上所述，最终的应力-应变关系为

(k=1,2,3)

(27)

反应在雅克比矩阵∂Δσ/∂Δε中即为

(28)

式中：dt为积分时间步长，[I]为6×6的单位矩阵。

2.3 模型算法与程序编制

在ABAQUS软件中编辑UMAT子程序来实现Davidenkov模型，其具体的算法步骤如下

(1) 在ABAQUS中输入Davidenkov模型所需的土体初始的动力参数，包括初始剪切模量Gmax，泊松比ν，拟合参数A，B，γ0，剪应变上限γult，Rayleigh阻尼系数α1；

(2) 调用主程序，读取当前步的应力、应变及应变增量；

(4) 计算d值，若d值小于0，则荷载转向，此时记忆新的广义剪应变γc；

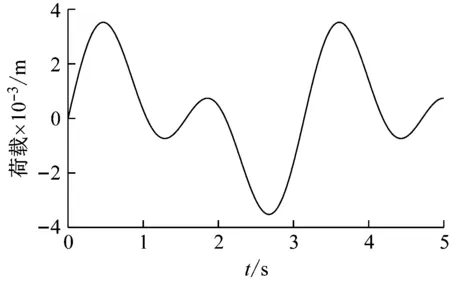
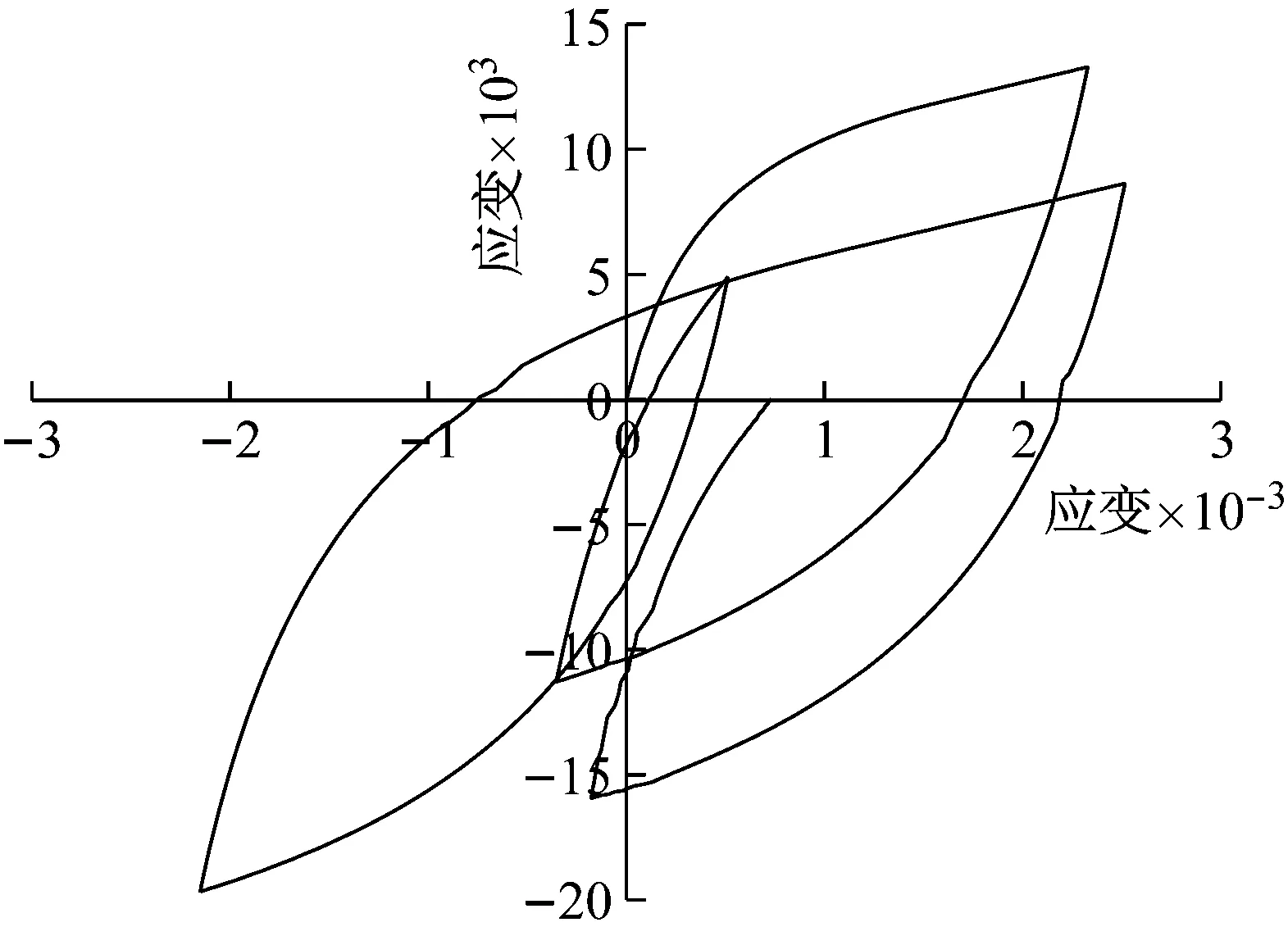
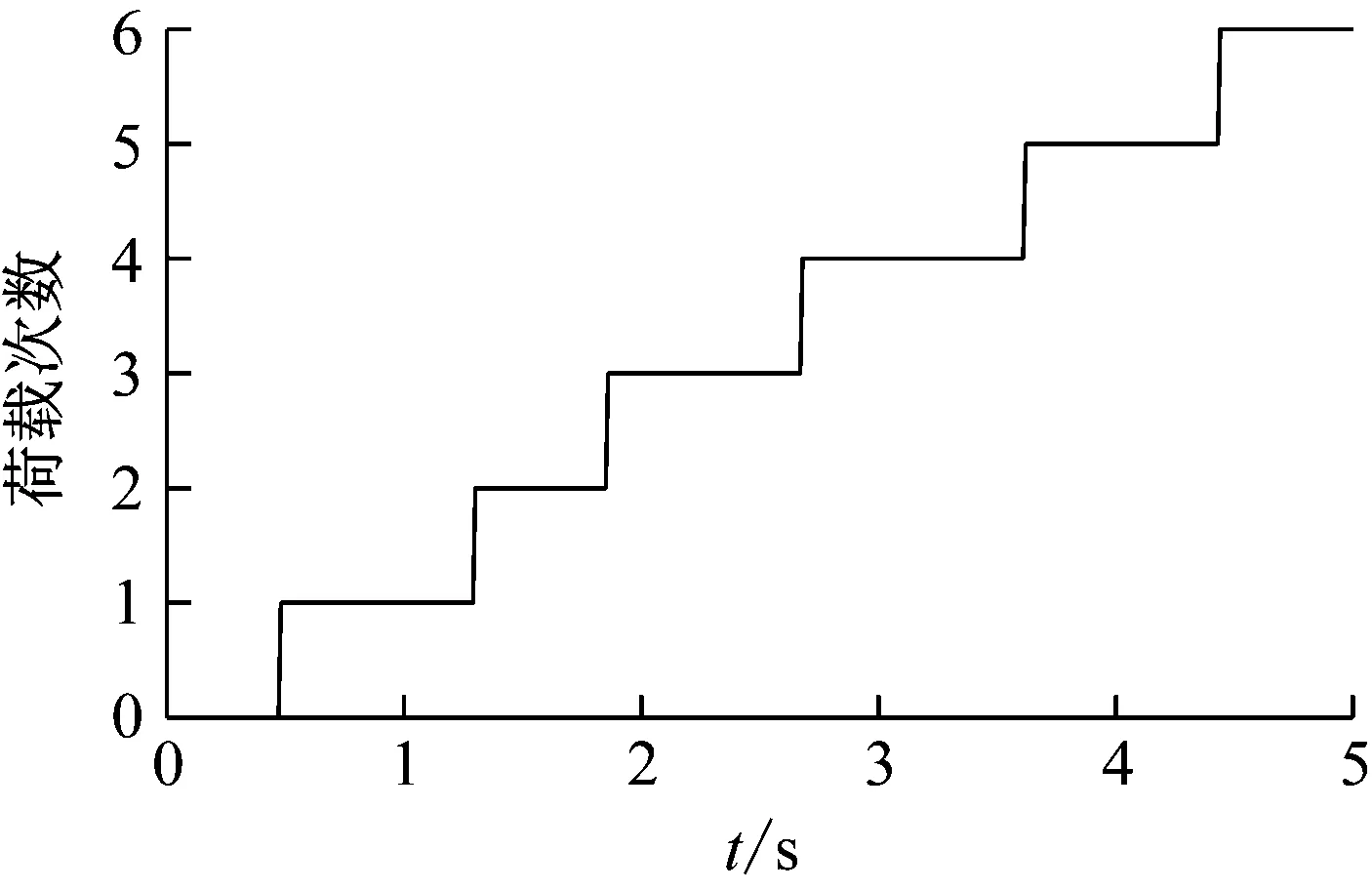
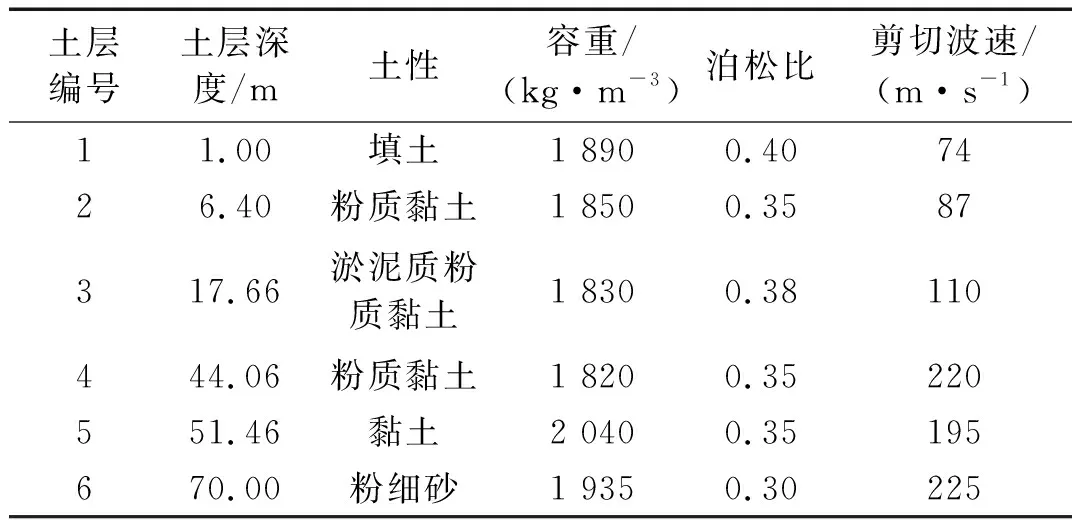
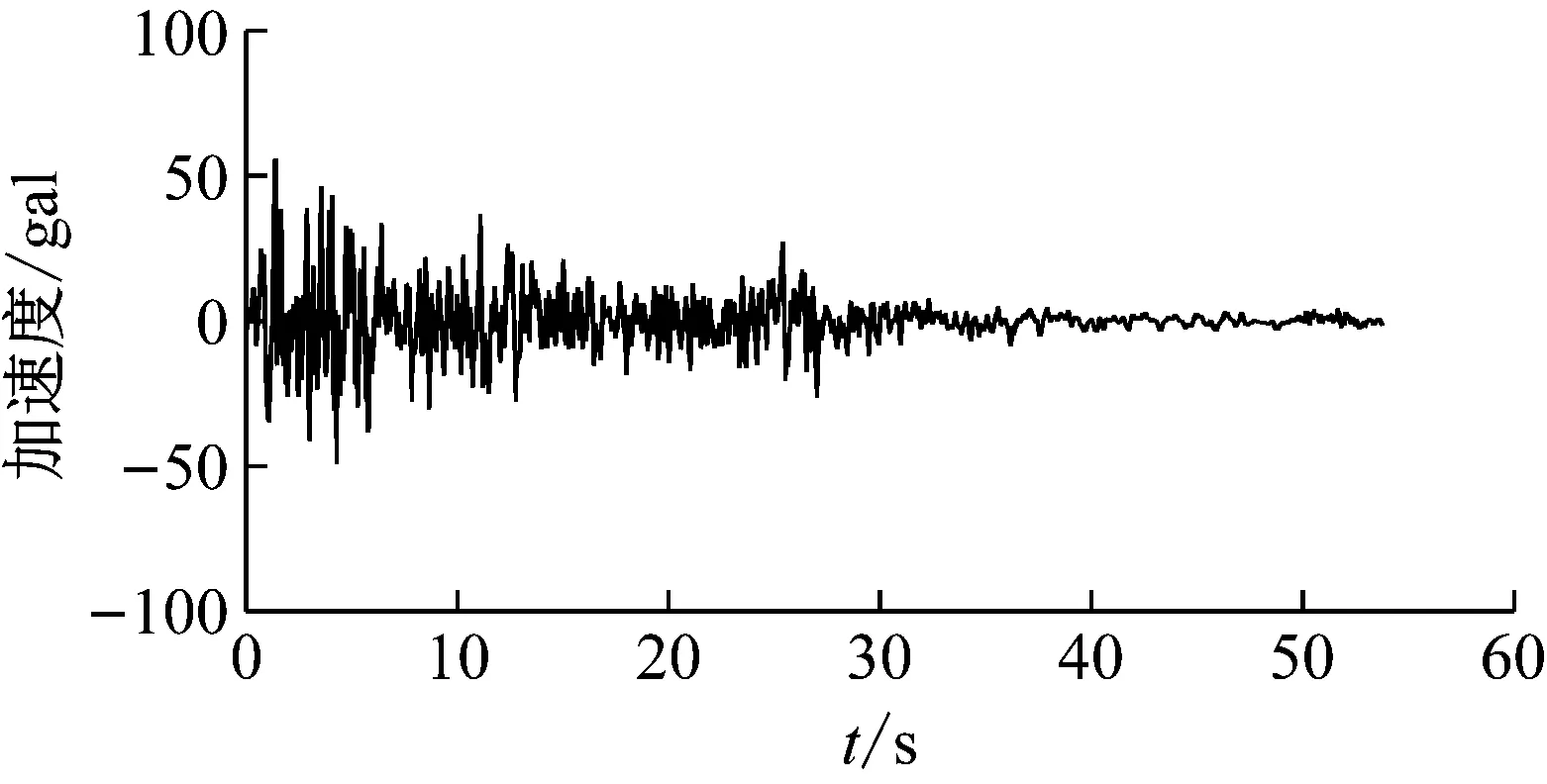
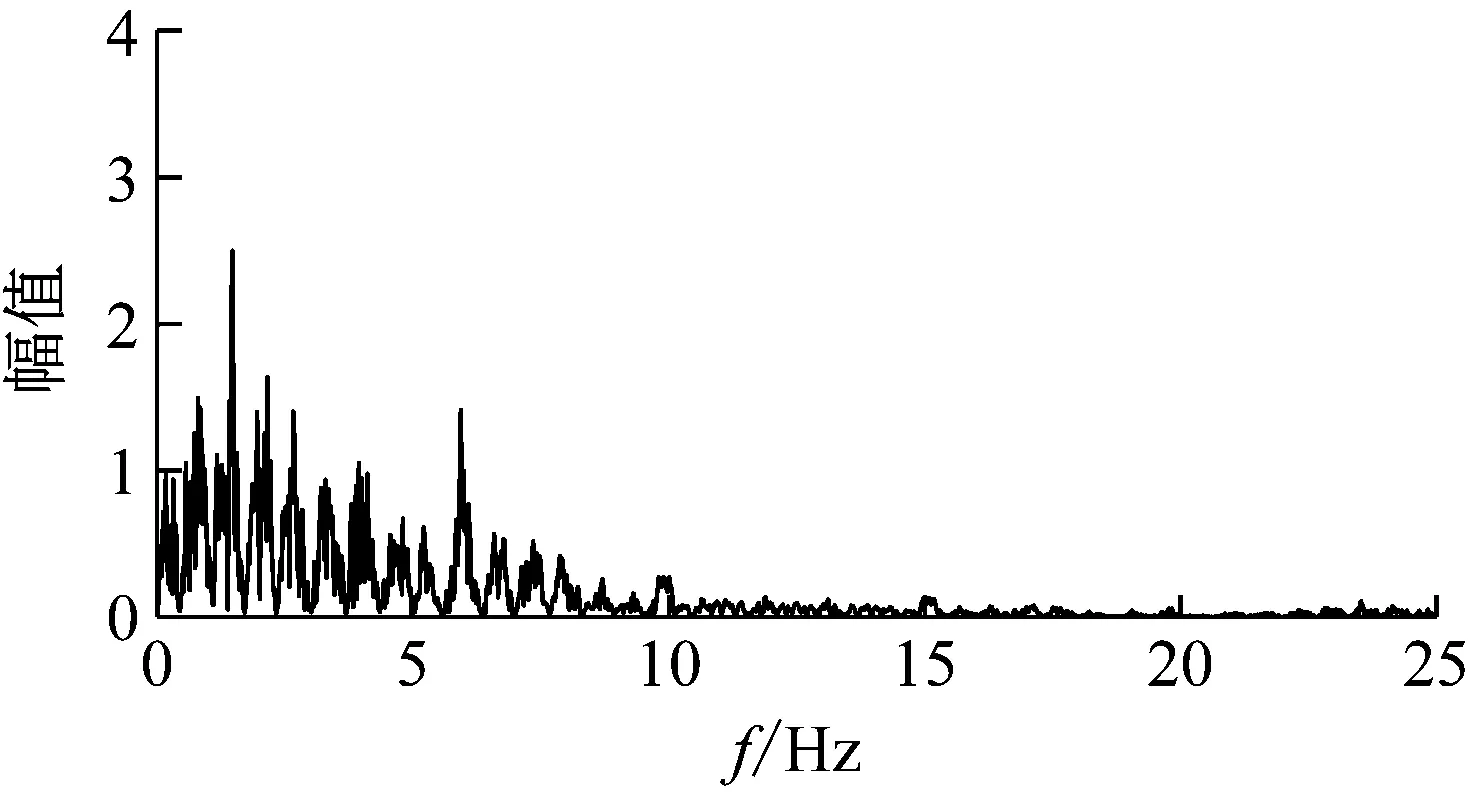
(5) 计算土体在初始加载、卸载和再加载条件下的剪切模量G，为了保证计算的稳定性，可取一剪切模量小值Gmin，如果G

(6) 计算拉密常数，更新雅克比矩阵；

(7) 更新内能及状态变量。

该模型的计算流程图如图5所示，在Davidenkov本构模型子程序的编辑中，会用到大量的状态变量数组，这些状态变量数组可以用来存储与求解过程有关的参变量，这些参变量会随着求解过程而更新，如在判断是否荷载转向时，应变增量及新的γc即可用状态变量保存调用，并可在结果文件中输出，用户可以清楚的知道荷载在何时发生转向，极大的方便了用户的编辑及查错过程。

图5 子程序计算流程图

2.4 程序验证

为验证子程序的可靠性，本文首先利用一个单元进行验证计算，因为一个单元的应力应变状态简单，能够更直观的反应子程序是否能够实现刚度折减及荷载转向等功能。在ABAQUS中建立一个1 m×1 m×1 m的单元，通过施加位移荷载的形式来研究复杂加载条件下的应力-应变变化情况，荷载路径采用如下形式，路径图如图6所示。

y=2e-3×(sin(2x)+sin(4x))

(29)

图6 荷载路径图

图7是单元在荷载作用下刚度折减情况，可以看到，随着荷载的增加，土体单元的刚度会随之衰减，当荷载转向时，土体的刚度也随之发生变化，当土体刚度小于初始刚度的5%时，土体刚度为一定值(Gmin)不再降低。

图7 刚度折减曲线

图8是单元的应力-应变关系曲线，可以看到，土体单元的应力-应变关系存在明显的滞回现象，滞回圈饱满。图9是通过状态变量记录到的荷载转向的次数，将其与输入荷载对比，可以看出，本文的子程序能正确对土体单元的加卸载情况进行判断。

图8 应力-应变关系曲线

图9 荷载转向次数

3 软土计算结果对比

本文选取了典型上海软土场地进行二维地震反应有限元分析，并将分析结果与等效线性化结果对比。典型上海软土场地各层土的物理力学参数见表5所示，各层土的基于Davidenkov模型的参数拟合结果详见表4。

表5 典型上海软土场地物理力学参数

本文利用作者文献[20]中得到的基岩地震波作为输入，进行二维软土场地地震反应分析，并将非线性动力本构模型的计算结果和等效线性化结果进行对比。选用基岩地震波的加速度时程曲线及傅里叶谱分别如图10和图11所示。

图10 基岩地震波时程曲线

图11 基岩地震波傅里叶谱

图12和图13分别是经过等效线性化算法和本文子程序计算得到的地表的加速度时程响应曲线和地表相对位移时程响应曲线。二者的响应峰值及相对差别列于表6中。

图12 加速度响应对比

图13 相对位移响应对比

Tab.6 Comparison between equivalent linearization results and subroutine results

对比类别地表加速度响应/gal地表相对位移响应/m等效线性化结果94.460.044本文子程序结果83.340.039相对差13.34%12.82%

由表6可知，采用等效线性化和本文子程序计算的地表加速度响应峰值分别是94.46 gal和81.34 gal，二者相对差为13.34%；采用等效线性化和本文子程序计算的地表相对位移响应峰值分别是0.044 m和0.039 m，二者相对差为12.82%。这主要是由于等效线性化方法会产生“虚(拟)共振效应”,过高地估计地震反应。

4 结 论

通过本文的研究，可以得到以下结论：

(1) 本文推导了Davidenkov模型的非线性动力本构模型在初始加载、卸载和再加载阶段的增量剪切模量表达式，并将土体动应力-应变关系推广到三维。基于粒子群优化算法对Davidenkov模型的参数进行拟合，并通过典型砂土和黏土验证了拟合效果。结果表明，两种土体拟合结果的互相关度量值NCC均接近于1，粒子群优化算法对Davidenkov模型参数具有很好的拟合效果。

(2) 利用ABAQUS软件提供的二次开发平台UMAT，本文编制了基于Davidenkov模型的土体非线性动力本构模型计算子程序，并通过复杂加载路径验证了该子程序的正确性，实现了在ABAQUS软件中软土非线性动力本构模型的二次开发。

(3) 以某典型上海软土场地为例，文中对比分析了上海软土场地基于非线性动力本构模型的计算结果和等效线性化的结果。结果表明，上海软土场地基于非线性动力本构模型的加速度响应值和相对位移响应值要小于等效线性化的结果。