两种计算程序对弱非线性硬场地地震响应的计算比较*

于啸波，孙 锐，袁晓铭，陈龙伟

(中国地震局工程力学研究所地震工程与工程振动重点实验室，黑龙江哈尔滨150080)

0 引言

土层地震动计算在地震工程中具有重要意义。常用的地震反应分析方法是一维等效线性化方法(齐文浩，2004)，LSSRLI-1与SHAKE2000是这种方法的代表程序 (廖振鹏，1989):前者代表了20世纪90年代的国际水平，是我国目前工程地震安全性评价工作规定使用的分析程序;后者最初由Schnable等 (1972)编写，并陆续推出了91、2000等改进版本，代表着目前国际上的先进水平，这两个程序都能在一定工况下得到可信的结果。按照我国抗震规范美国La Cienega台阵场地属于Ⅱ类场地，该台阵记录到了1999年M7.1地震从地下252 m处到地表的地震动，地下记录输入到SHAKE91中，计算得到的地表地震动与实际记录较吻合 (Haddadi，Shakal，2006)。将位于Ⅱ类场地响嘡台阵3号测井的地震记录输入到LSSRLI-1与SHAKE91中，地表反应都与记录相近，这表明输入地震动强度较低时，LSSRLI-1与SHAKE91可以基本满足工程需要 (齐文浩，2004)。以上结果都是基于计算与实测的对比，从一个侧面证明了两程序的可靠性，但存在实测记录少、工况数量不足的局限。

鉴于我国井下台阵较少，一些学者在没有强震记录的情况下，也进行了一些两程序间的对比分析，李亚东 (2011)对LSSRLI-1与SHAKE91进行比较发现，LSSRLI-1结果偏大，特别是在土层刚度小强震作用下更明显。另外，LSSRLI-1在计算中还可能出现计算不收敛情况 (齐文浩，2008)。但是，目前对于SHAKE与LSSRLI-1的对比分析，还缺乏系统性，没有进行深入的对比及分析差异原因。

场地条件对于等效线性化计算分析会有较大的影响 (景立平等，2005)。实际场地有不同分类方式，除去软、硬夹层等特殊情况 (李恒等，2014)，大致可分为软硬两种类型 (岩土工程勘察规范，GB50021—2001)。在我国抗震规范中，场地分类与岩土勘察规范的意义有所不同，不仅考虑岩土体的剪切波速，还考虑了覆盖层的厚度。Ⅰ、Ⅱ类场地土层具有相对高的剪切波速，覆盖层厚度相对小，是抗震有利的场地。以往的研究结果显示，在较硬场地上，等效线性化方法往往能够有较好的表现 (齐文浩，2004;Haddadi，Shakal，2006)，但由于对比的工况较少，仍需进一步研究。理论上来讲，等效线性化方法更适用于土的动力非线性较弱时，即土的模量衰减与阻尼比的增长曲线相对平缓，而硬场地往往具有这样的动力特性。本文选择较硬的Ⅰ、Ⅱ类场地为研究对象，并将这些工况简称为弱非线性硬场地。

本文以构造的2个Ⅰ类和4个Ⅱ类场地土层剖面为研究对象，输入3种不同频率类型的地震波，采用两种等效线性化分析程序 LSSRLI-1与SHAKE计算土层地震动，以期掌握两种典型土层地震反应分析方法的异同性。

1 计算理论与计算模型

1.1 水平成层土中波动方程的解

LSSRLI-1与SHAKE2000都是一维土层反应分析程序，以一维剪切波在水平成层介质中的地震反应稳态解为基础编制的。

首先，底层输入频域地震位移为ENexp(ikNz)的地震波时，第n层地震波位移的频域稳态一般解为

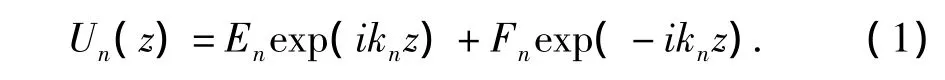
式中，kn=(1-idn)·ω/cn，dn为第n层的阻尼比;cn=(1+idn)，μn为第 n层剪切模量。En、Fn为波幅系数，需要用传递矩阵进行求解:

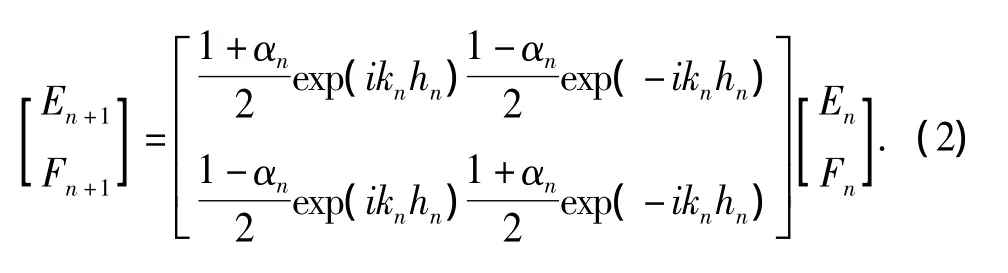
式中，αn=ρncn/ρn+1cn+1，为相邻两层的复波阻抗比值。(2)式右边左乘的矩阵可以根据每一层的土层信息计算出来。根据 (2)式由E1、F1推出各层的En、Fn。但E1、F1开始是未知的，需要根据已知的波幅系数EN来得到，关系如下

式中，EN为已知的输入地震波波幅系数;eN通过(2)式中的传递矩阵得到。由 (2)、(3)式可递推出从1层到N层的波幅系数E、F。这样可以通过 (1)式得到各层的位移，再进行傅式逆变换就得到了时域位移，进而可得速度、加速度。但是因为实际的土层是非线性系统，因此叠加原理失效，不能进行傅式变换，所以需要引入等效线性化的假设，让系统成为可以使用傅式变换的线性系统 (廖振鹏，2003)。

1.2 计算模型

根据建筑抗震设计规范 (GB50011—2010)中场地分类的条款，构造了2个Ⅰ类、4个Ⅱ类场地的土层剖面。Ⅰ类场地模型因为比较薄，所以在程序中仅分为4个计算层，前3层为土层，第4层为基岩，土的物理力学特征见表1。Ⅱ类场地模型的计算层厚度一般为每层2～3 m，土层物理力学特征见表2。

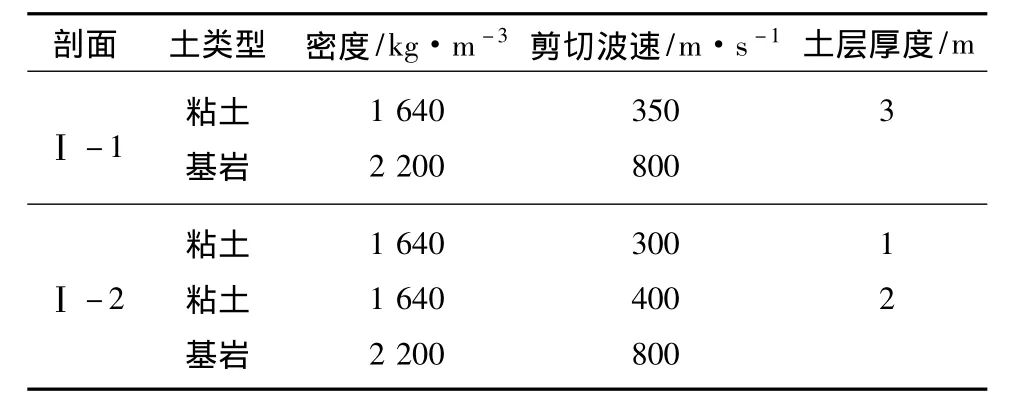
表1 Ⅰ类场地土层的物理力学性质Tab.1 Physical and mechanical properties of class-I sites

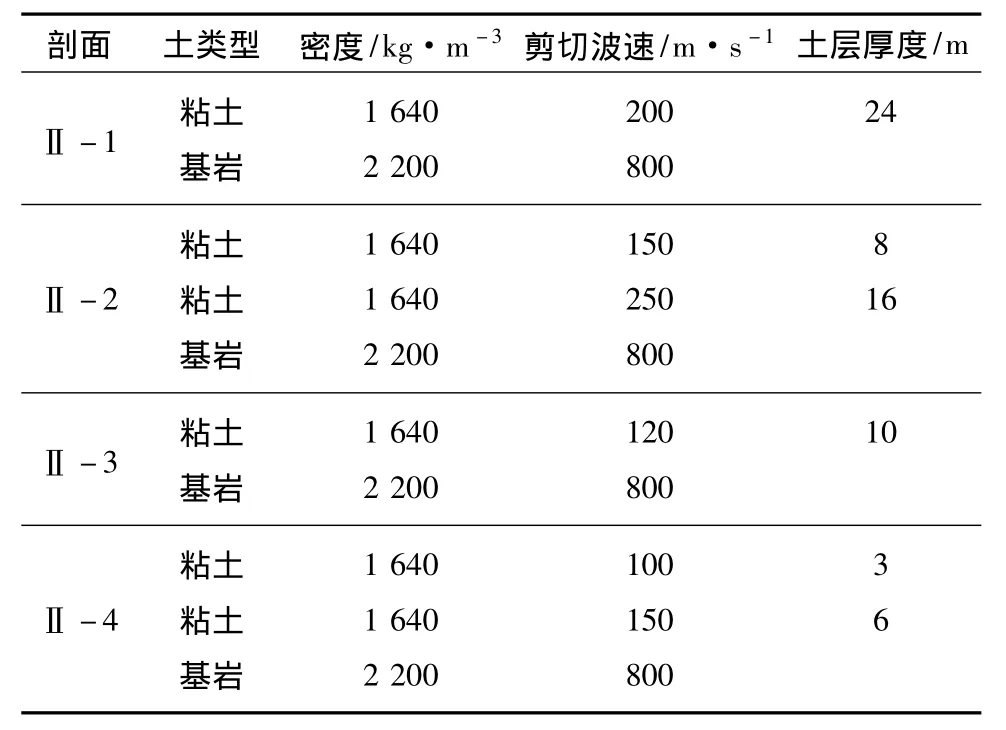
表2 Ⅱ类场地土的物理力学性质Tab.2 Physical and mechanical properties of class-II sites

考虑到输入地震波对两程序计算结果 (PGA、反应谱和剪应变)差异程度有影响，输入的地震波需要具有一定的代表性。本文选择5%阻尼比反应谱中长周期成分占优、短周期成分占优以及成分比较均匀的地震波，确定输入地震波为El-Centro地震波、AKTH19地震波和KSRH地震波(图1)。AKTH19与KSRH均为日本Kik-net台站代码，输入地震波信息见表3。从反应谱来看 (图2)，KSRH地震波短周期成分丰富，AKTH19地震波长周期成分丰富，El-Centro地震波介于之间，以此代表频率成分不均匀的地震波。将地震波都调幅至0.1 g、0.2 g与0.4 g进行输入，分别代表Ⅶ、Ⅷ和Ⅸ度区。这样，Ⅰ类场地的两个剖面、3条地震波和3个幅值，共有18个组合工况，同样Ⅱ类场地共有36个组合工况。

本文使用的非线性曲线是陈红娟 (2009)提出的粘土的模量衰减曲线上限与阻尼比增长曲线的下限的组合，代表着土为弱非线性的情况，数值如表4所示。

表3 输入地震波基本信息Tab.3 Basic information of the inputting waves

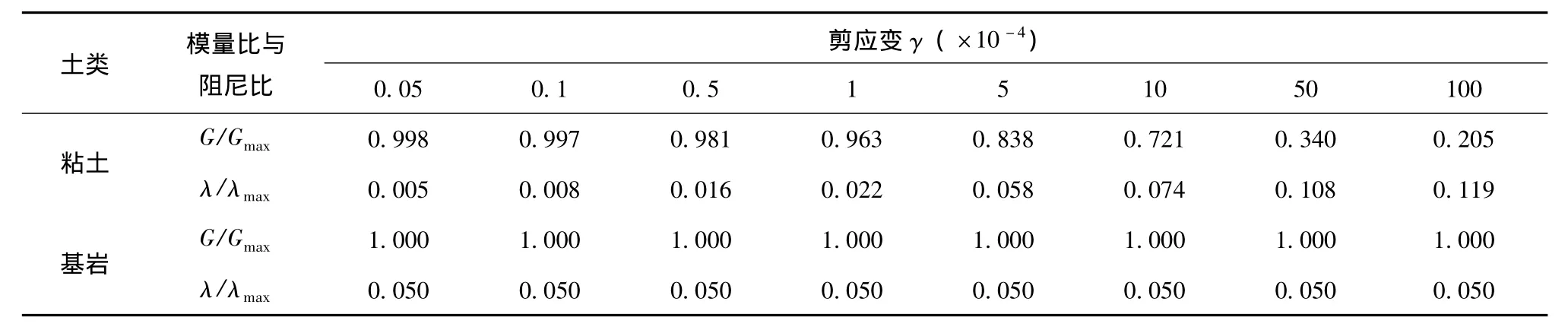
表4 土层非线性曲线Tab.4 Non-linear curves of profiles

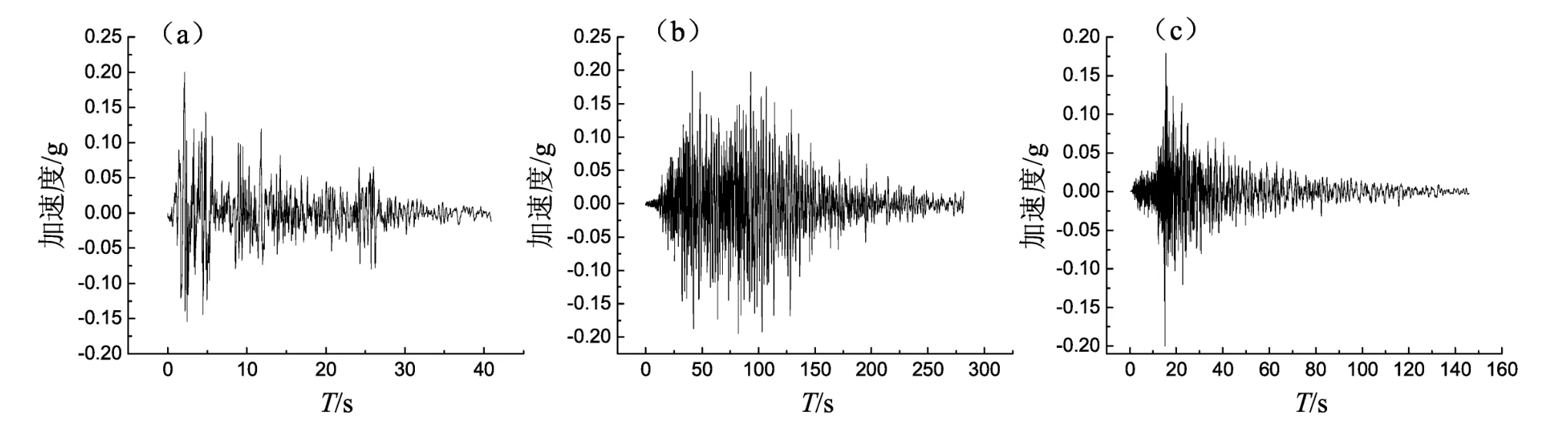
图1 输入El Centro(a)、AKTH19(b)和KSRH(c)不同地震波时的波形Fig.1 Waveform of the inputting El Centro(a)，AKTH19(b)and KSRH(c)earthquakes

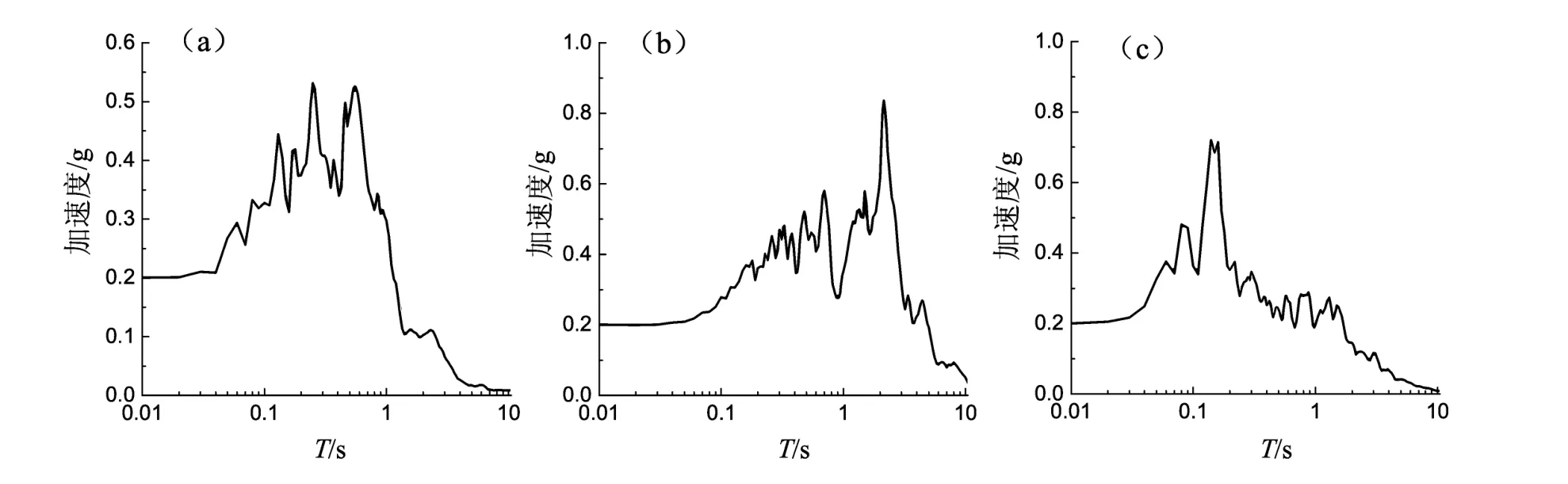
图2 输入El Centro(a)、AKTH19(b)和KSRH(c)不同地震波时的加速度反应谱 (5%阻尼比)Fig.2 Acceleration response spectrum of the inputting El Centro(a)，AKTH19(b)and KSRH(c)earthquakes(5%damping ratio)

2 结果比较

本文主要比较LSSRLI-1与SHAKE两个程序计算出的地表加速度峰值、加速度反应谱和最大剪应变。相对差以SHAKE2000结果作为基准进行计算。

2.1 加速度峰值

结果表明，两个程序计算出的Ⅰ类场地的地表加速度峰值PGA的相对差变化范围是 (0～1.4)%，平均值为0.6%，差异很小。从图3可见，加速度峰值的相对差随埋深变化，而且靠近地表的时候相对差较大;剖面Ⅰ-2的相对差都比较小，沿深度变化不大。

两个程序计算出的Ⅱ类场地的地表加速度峰值PGA的相对差变化范围是 (0.03～30.7)%，平均值为6.6%，可以看出，与Ⅰ类场地相比，差异程度的变化范围变大。由图4可见，不同深度相对差有所不同，而且最大的相对差并不一定出现在地表处。

不同输入地震波对PGA结果的影响见图5。由图可见，输入3种地震波的计算结果具有很相近的分布，相对差都集中在10%以内。这表明，在弱非线性硬场地条件下，对于不同地震波，LSSRLI-1与SHAKE2000的大部分PGA计算结果是相近的。

2.2 反应谱

为了对比反应谱间的差异，得到两个程序计算的地表加速度反应谱的谱值比为

其中，SS是SHAKE2000的反应谱结果 (g)，SL是LSSRLI-1的反应谱结果 (g)。

图3 Ⅰ类场地加速度峰值相对差随埋深的变化Fig.3 Relative difference of acceleration peak value varies with depth in class-I sites

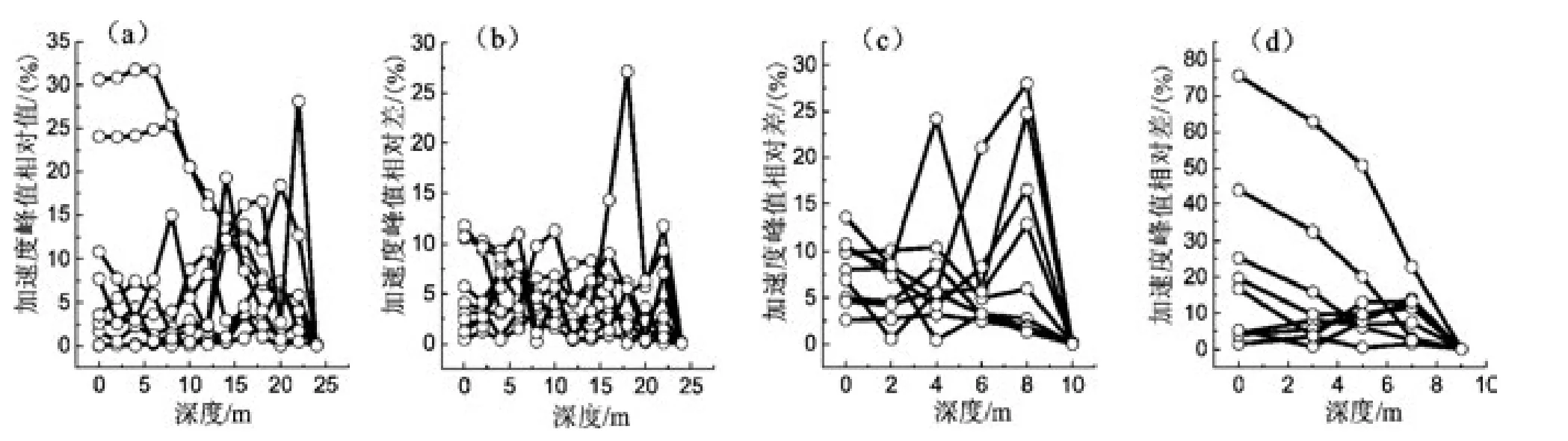
图4 Ⅱ类场地加速度峰值相对差随埋深的变化Fig.4 Relative deviation of acceleration peak value varies with depth in class-II sites

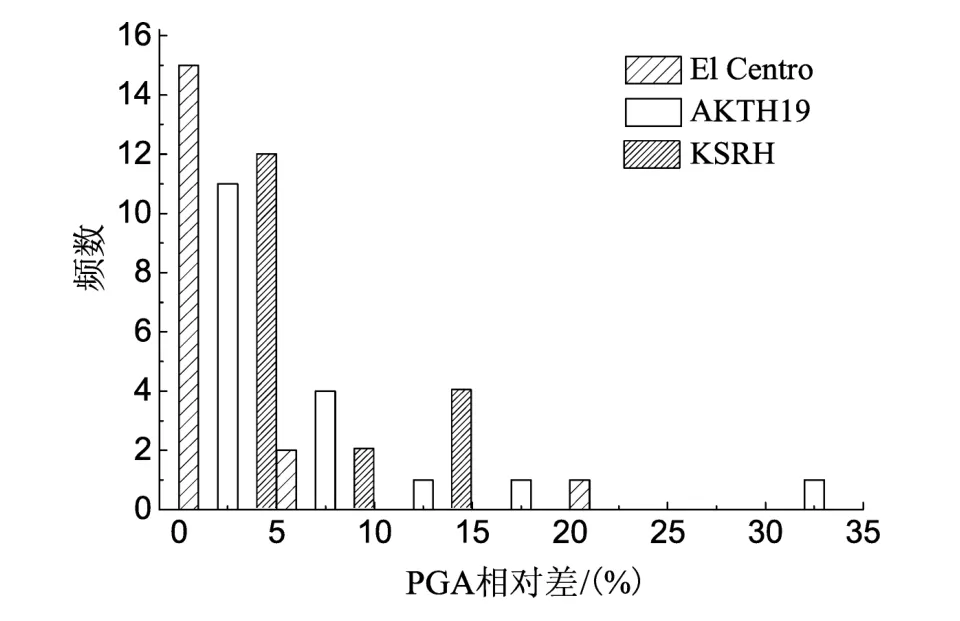
图5 不同输入地震波下Ⅰ、Ⅱ类场地加速度峰值相对差统计直方图Fig.5 Relative deviation histogram of acceleration peak in class-Ⅰ and class-Ⅱsites under different inputting waves

本文进一步采用平均谱值比来表示两种程序计算的加速度反应谱的平均差异，按下式计算:

计算表明，Ⅰ类场地平均谱值比均值是0.3%，变化范围是 (0.1～0.6)%;Ⅱ类场地的平均谱值比均值是2.3%，变化范围是 (0.2～12.3)%。

图6a是Ⅰ类场地计算结果。从各工况结果可见，在周期T=0.03 s附近，RS=0.6(相当于相对差为45.1%)，两程序在这个周期附近的反应谱结果差异较大;0.1 s之后，反应谱结果差异很小。

图6b是Ⅱ类场地计算结果。从各工况结果的曲线看，反应谱结果的相对差在3 s以前存在较大的波动，与Ⅰ类场地相比，反应谱的较大差异从短周期段发展到了长周期段。

谱比值反映的是反应谱间的相对差，不同输入地震波下Ⅰ、Ⅱ类场地反应谱相对差统计结果见图7。由图可见，输入3种地震波计算的结果具有相近的分布，而且不超过20%。这表明，在弱非线性硬场地条件下，两个程序在输入不同地震波时，反应谱计算结果是相近的。

2.3 最大剪应变

LSSRLI-1与SHAKE2000给出了每一计算层内的剪应变峰值，在不同埋深处，剪应变峰值也不同，笔者对剪应变峰值随埋深变化曲线上的最大值进行比较。结果表明，Ⅰ类场地剪应变相对差变化范围是 (0.7～9.0)%，均值为4.4%;Ⅱ类场地的剪应变相对差变化范围是 (0.7～303.0)%，均值为46.4%。

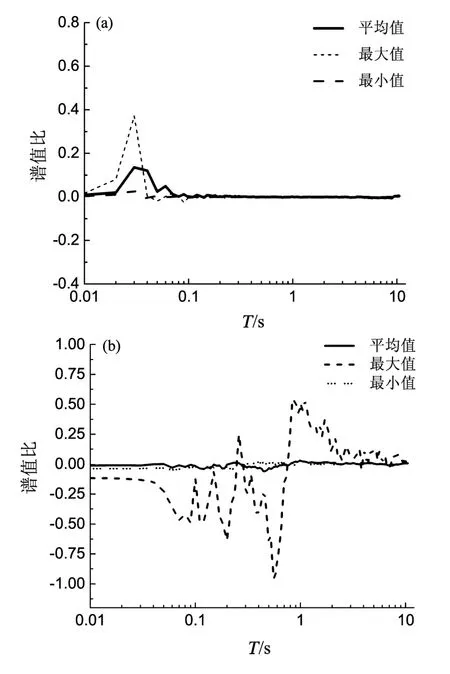
图6 Ⅰ类 (a)、Ⅱ类 (b)场地反应谱谱值比汇总Fig.6 Spectral ratio of response spectrum of class-Ⅰ(a)and class-Ⅱsites(b)

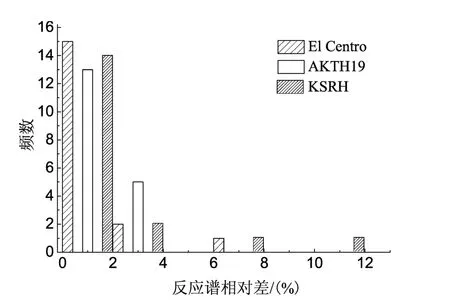
图7 不同输入地震波下Ⅰ、Ⅱ类场地反应谱相对差统计直方图Fig.7 Relative deviation histogram of response spectrum in class-Ⅰ and class-Ⅱsites under different inputting waves

图8为最大剪应变相对差的频率分布直方图，从图中可以看出两个程序计算出的最大剪应变在Ⅰ类场地上比较相近，相对差在10%内波动 (图8a);而Ⅱ类场地的相对差变化范围则较大，主要集中在50%以内，但最大可达300%(图8b)。

按照不同的输入地震波，将剪应变峰值相对差进行统计，结果见图9。由图可见，3种地震波造成的剪应变峰值差异程度具有相近的分布，但剪应变峰值相对差大于100%的情况均来自于KSRH地震波输入。

2.4 剪应变相对差与PGA、反应谱相对差的相关性

经过对比分析发现，剪应变、反应谱和PGA相对差间有一定的关联，其中一个较大时，其余两个也较大。图10a、b给出了一工况中剪应变差异与相应的反应谱差异，从图中可以看出，SHAKE2000计算得到的最大剪应变为17.7×10-4，而LSSRLI-1为17.6×10-4，相对差为0.5%。SHAKE2000计算的PGA为0.28 g，LSSRLI-1也为0.28 g，结果相同。反应谱最大相对差为16%。图10c、d为另一工况的计算结果，由图可知，SHAKE2000计算得到的最大剪应变为83.1×10-4，而LSSRLI-1的为144×10-4，相对差为72.6%;SHAKE2000计算的PGA为0.81 g，而LSSRLI-1的为0.61 g，两者之间的相对差为24%。反应谱最大相对差为59%。由此可见，当剪应变差异越大，则PGA和反应谱的差异越大，三者之间存在一定的关联性。

2.5 差异原因初步分析

两个程序的基本原理相同，输入的参数相同，计算结果的差异极有可能是程序内部某些参数的计算方法或算法不同造成的。在迭代过程中，会变化的参数是根据等效剪应变来取值的土层模量比、阻尼比。等效剪应变计算都是剪应变峰值乘以折减系数，计算中该系数均为0.65，即等效剪应变计算方法相同。但从前文第2.3节可以看出，两程序的剪应变峰值是不同的，所以两程序迭代计算得到的等效剪应变也是不同的。因此，迭代中剪应变的不同计算方法是导致不同计算结果的原因。此外，迭代中模量比、阻尼比的插值方法也可能不同。有研究表明，土层地震反应结果对模量比与阻尼比很敏感(刘红帅等，2005;孙锐等，2009)，这也能导致两程序的计算结果有差异。

图8 Ⅰ类 (a)、Ⅱ类 (b)场地最大剪应变相对差频率分布直方图Fig.8 Frequency distribution histogram of maximum shear strain deviation in class-Ⅰsite(a)and class-Ⅱsite(b)

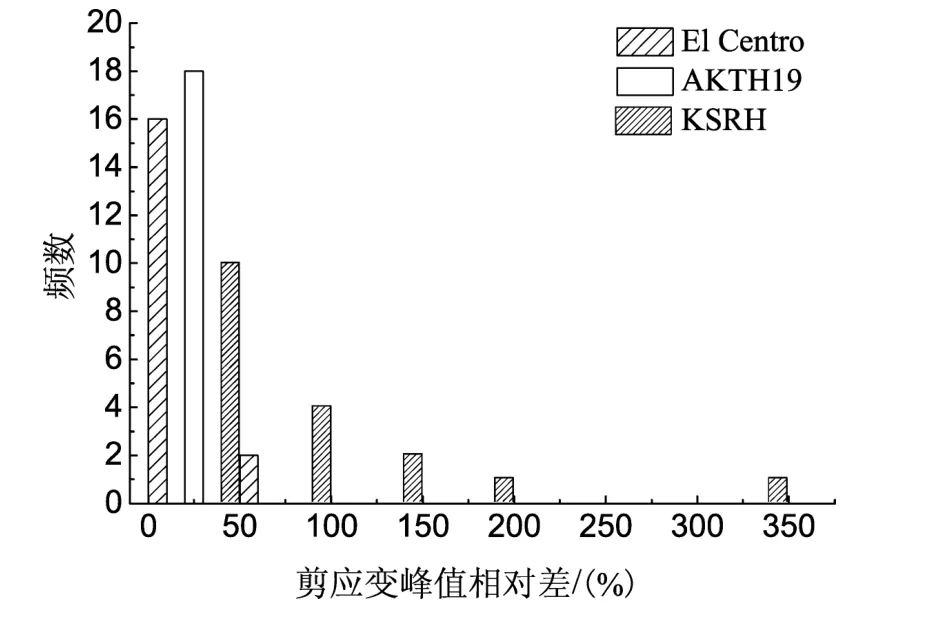
图9 不同输入地震波下Ⅰ、Ⅱ类场地剪应变峰值相对差统计直方图Fig.9 Relative deviation histogram of shear strain peak in class-Ⅰ and class-Ⅱsites under different inputting waves

为了表明两程序的计算结果差异来自内部计算方法不同，笔者给出一个算例。采用图10c、d的工况，即在剖面Ⅱ-1输入0.4 g的El-Centro地震波。在这个工况中，SHAKE2000与LSSRLI-1的计算结果经过若干次迭代已经收敛，现称图10c、d中的结果为“收敛结果”。在两程序已经收敛的结果上，用SHAKE2000再将其各自迭代一次，称这次结果为“再迭代结果”。如果SHAKE2000与LSSRLI-1内部计算方法相同，那么LSSRLI-1的再迭代结果应该与LSSRLI-1的收敛结果相同或相近。实施这次“额外”迭代的具体做法如下:将图10c中SHAKE2000与LSSRLI-1的各层剪应变计算结果提取出来，结合前文给出的土非线性曲线 (等效剪应变系数取0.65)，可以插值获得对应两个程序中各土层的剪切模量与阻尼比，见表5。将这些模量与阻尼比当作初始参数都输入到SHAKE2000中进行1次迭代计算，LSSRLI-1的再迭代计算流程见图11。因为只有1次迭代，所以剪应变计算结果只由各程序的剪应变计算方法决定，排除了多次迭代带来的其他差异累积，同样的还有反应谱的计算结果。剪应变、反应谱收敛、再迭代结果见图12。

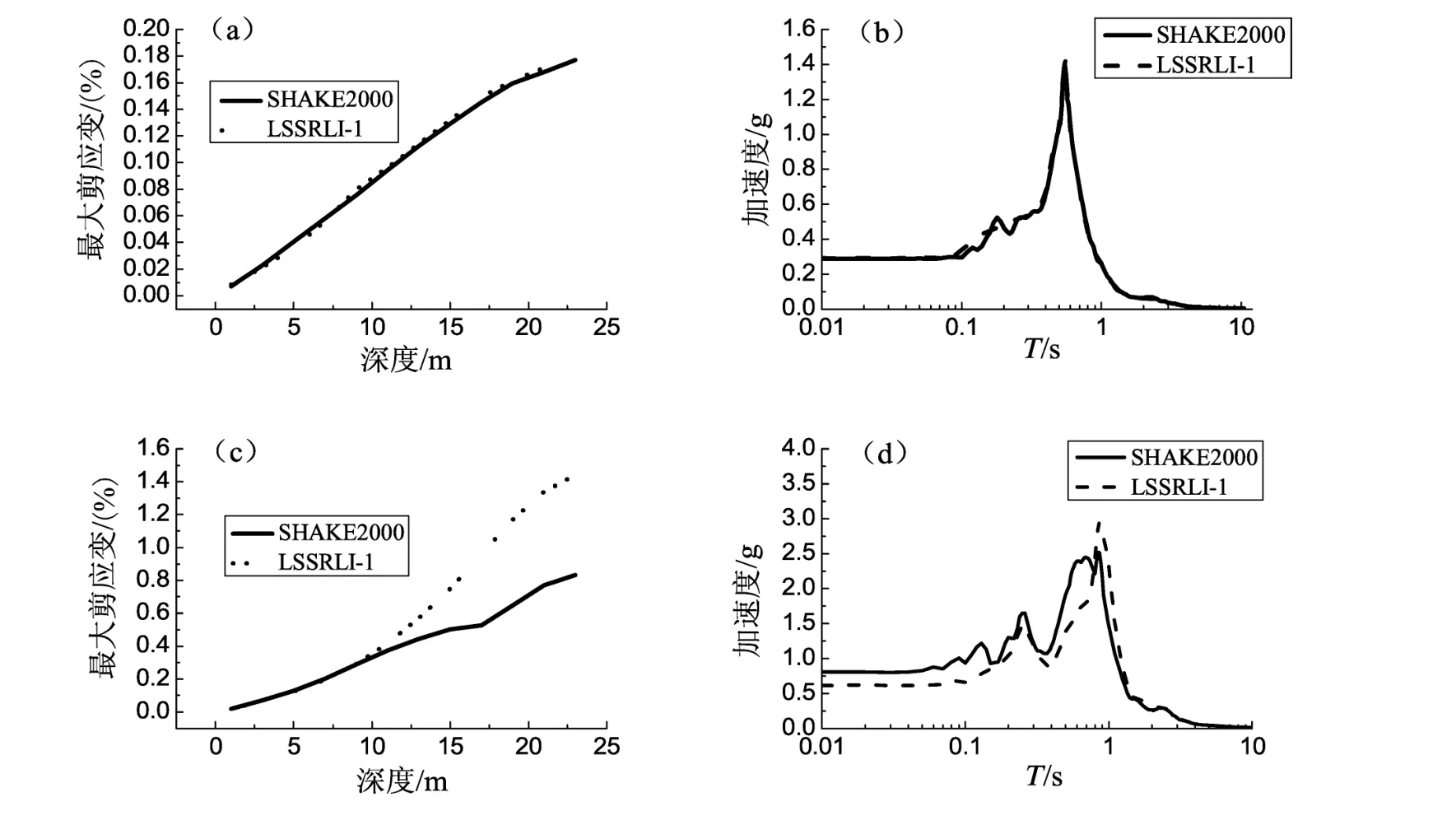
图10 剖面Ⅱ-1输入El-Centro地震波的剪应变及反应谱Fig.10 Shear strain and response spectrum of inputting El-Centro wave in profileⅡ-1

图11 对LSSRLI-1收敛结果实施再迭代流程图Fig.11 Flow chart for re-iterate on convergence results of LSSRLI-1

图12 中的LS代表输入表5中LSSRLI-1收敛结果的G、D列，再用SHAKE2000进行1次计算的再迭代结果，第一个L代表使用LSSRLI-1的收敛结果，第二个S代表用SHAKE2000进行计算;L代表图10c、d中LSSRLI-1收敛结果;SS、S具有相似的意义，代表SHAKE2000相关结果。dS与dS1代表剪应变与反应谱中 SS与 S的差距，即SHAKE2000再迭代结果与其收敛结果的差距;dL与dL1代表各图中LS与L的差距，即LSSRLI-1再迭代结果与其收敛结果的差距;dLS与dLS1代表各图中L与S的差距，即图10c、d中SHAKE2000与LSSRLI-1收敛结果的差距。

表5 从各层的剪应变计算对应的剪切模量G、阻尼比DTab.5 Shear modulus G and damping ratio D calculated by shear strain in every layers

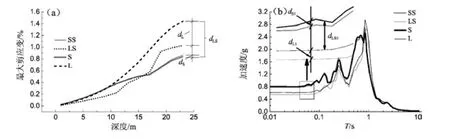
图12 不同迭代次数下剪应变结果 (a)和反应谱结果 (b)(剖面Ⅱ-1输入El Centro地震波)Fig.12 Shear strain(a)and response spectrum results(b)under different iteration number(inputting El Centro wave in profileⅡ-1)

在图12a中SS与S很接近，即dS很小，这说明SS仅仅是在S本已收敛的结果基础上又迭代了一次;而LS与L有大的偏差，与dS相比，dL很大，这说明SHAKE2000程序与LSSRLI-1程序具有不同的剪应变计算方法。而从图12b中可以看到，SS与S的反应谱很接近，dS1很小，而LS与L之间的距离则略大，dL1＞dS1。SS与S的反应谱也仅仅是多迭代一次而已，所以很接近;而LS与L反应谱有较小的差异，可能是由输入参数上存在的误差导致，也可能是反应谱计算方法存在不同，这些需要进一步研究。

从以上的对比可知，当剪应变不参与计算，即不依据剪应变来插值求得下一次计算所需各层土的剪切模量和阻尼比时，两程序计算结果并无太大差异，如图12b中L与LS两条线已非常相近。但剪应变参与到计算当中时，两方法所得到的地表反应就相差较大，如图12b中S与L两条反应谱。因而，可以初步推断，造成两程序间差异的主要原因是剪应变计算方法不同，当然，算法等方面也会有一些差异，但所带来的影响并不大。

3 结论

本文讨论了土为具有弱非线性的硬场地 (Ⅰ类、Ⅱ类场地)下采用LSSRLI-1与SHAKE2000计算土层地震动的异同性，主要结论为:

(1)Ⅰ类场地两个程序计算出的PGA十分接近，相对差变化范围不超过1.4%，平均值为0.6%;Ⅱ类场地两程序间平均相对差为6.6%，可以忽略，但在某些情况下较大，达到30%。

(2)Ⅰ类场地两个程序计算出的反应谱差别很小，谱值比均值是0.3%，变化范围不超过0.6%;Ⅱ类场地的反应谱存在差异，平均谱值比均值是2.3%，变化范围是0.2%～12.3%。

(3)两个程序计算出的Ⅰ类场地反应谱中，差异出现在0.1 s前，0.1 s后差异很小;Ⅱ类场地反应谱的差异则从小于0.1 s延伸到0.5 s之后，且差异程度增大。

(4)就两个程序计算出的最大剪应变而言，Ⅰ类场地相对差变化范围是 (0.7～9.0)%，均值为4.4%;而Ⅱ类场地的相对差则有明显增长，相对差变化范围为 (0.7～300)%，均值为46%。

(5)PGA相对差和反应谱相对差与剪应变相对差之间存在一定相关性。

(6)LSSRLI-1与 SHAKE2000计算结果不同，一个主要原因在于剪应变计算方法的不同，其他的原因需要进一步对程序研究。

陈红娟.2009.土动力非线性的变异性及其对地震动影响的概率分析［D］.哈尔滨:中国地震局工程力学研究所.

景立平，卓旭炀，王祥建.2005.复杂介质对地震波传播的影响［J］.岩土工程学报，27(4):393-397.

李恒，张静波，吴建超.2014.软夹层和硬夹层对地表地震动特性的影响［J］.地震工程学报，36(3):441-444.

李亚东.2011.区域性土的动力特性及对地下结构抗震分析的影响［D］.广州:广州大学.

廖振鹏.2003.工程波动理论导论(第二版)［M］.北京:科学出版社.

廖振鹏.1989.地震小区划理论与实践［M］.北京:地震出版社.

刘红帅，薄景山，吴兆营，等.2005.土体参数对地表加速度峰值和反应谱的影响［J］.地震研究，28(2):167-171.

齐文浩.2004.土层地震反应分析方法的比较研究［D］.哈尔滨:中国地震局工程力学研究所.

齐文浩.2008.土层非线性地震反应分析方法研究［D］.哈尔滨:中国地震局工程力学研究所.

孙锐，袁晓铭，刘晓键.2009.动剪切模量比与剪切波速对地震动影响及等量关系研究［J］.岩土工程学报，31(8):1267-1274.

Haddadi H.，Shakal A..2006.Analysis of some strong ground motion records obtained at CSMIP downhole arrays［C］//France:Third International Symposium on the effect of Surface Geology on Seismic Motion，Grenoble.

Schnabel P.B.，Lysmer J.，Seed H.B..1972.SHAKE:A computer program for earthquake response analysis of horizontally layered sites［R］//Report NO.EERC 72-12.Berkely:College of Engineering，University of California.

GB50011—2010，建筑抗震设计规范［S］.

GB50021—2001，岩土工程勘察规范［S］.