高速铁路水泥改良黄土路基长期动力稳定性评价

张沛云， 马学宁， 李善珍， 王 旭

(兰州交通大学 土木工程学院，兰州 730070)

高速铁路必须以舒适、可靠、安全及少维护性为前提条件，而路基作为轨道结构的基础，其性能直接影响线路的平顺性及轨道状态。我国黄土分布范围广，在黄土地区修建高速铁路所遇到的相关问题也越来越多，突出表现为沿线缺乏优良的A、B 组填料，而依靠外运合格填料既不经济也不合理，因此水泥改良土的应用得到迅速发展，基床底层填料改良已成为高速铁路路基设计的重要内容。

高速铁路无砟轨道路基设计需要充分考虑其动态响应，以确保交通荷载作用下的长期动力稳定。过去我国对铁路有砟轨道基床设计采用动强度作为控制指标，认为当路基动应力小于路基土临界动应力时，累积永久(塑性)变形会得到有效控制，路基长期动力稳定能得到保障，这种路基长期动力稳定性评价方法称为临界动应力法。杨广庆[1]对水泥改良土在列车重复荷载作用下的临界动应力、累计塑性变形、弹性变形和回弹模量的变化规律及影响因素进行了研究。冷伍明等[2]利用动三轴试验研究了振动荷载作用下重载铁路路基粗颗粒土填料不同含水率条件下的临界动应力。

而高速铁路无砟轨道路基对沉降的要求更为严格，在路基基床动应力满足临界动应力的要求，未达到强度破坏前，变形可能已经超过了无砟轨道允许沉降值。因此，在高铁无砟轨道基床设计中，除满足动强度要求外，还应同时满足动变形条件。而研究表明，当剪应变幅值超过某一临界值时，土结构或骨架将发生永久性(塑性)变形，根据剪切波传播理论，动剪应变幅可表示为振动速度与剪切波波速的比值，作为一个无量纲的参数，动剪应变幅同时反映振动荷载的大小和土的动力刚度的影响，是变形验算的最佳参数。

Vucetic[3]在分析、统计大量不同类型的土在动力循环荷载作用下室内试验结果的基础上，将土的反映用两个剪应变门槛参数即体积剪应变门槛γtv和线性剪应变门槛γtl来分类。胡一峰等[4-6]提出的土质路基动力稳定性评判准则，采用了疲劳动剪应变门槛作为评判条件。该准则认为，当路基动剪应变小于路基土疲劳动剪应变门槛时，基床是长期动力稳定的。刘晓红等[7]采用动剪应变法评价了武广高铁无砟轨道红黏土路堑基床的动力稳定性，并给出了不同物理状态下红黏土基床最小换填厚度的建议值。陈湘亮等[8]采用动剪应变法对武广高铁中弱-强风化泥质粉砂岩物理改良土进行综合评价。

目前关于水泥改良黄土的研究虽然很多，且已经在实际工程中得到一定程度的应用，但有关水泥改良黄土作为路基基床底层填料时的长期动力稳定性问题，目前几乎未见相关的文献报道，而要进行长期动力稳定性分析则需要相应的动力参数，故通过应力控制式疲劳动三轴试验对不同水泥掺量的改良黄土疲劳特性进行了研究，并分别基于临界动应力法和动剪应变法对高速铁路水泥改良黄土路基长期动力稳定性进行了综合评价，论证了水泥改良黄土作为高速铁路路基基床底层填料的可行性，为黄土地区路基填料的选择及路基设计提供了技术参考。

1 水泥改良黄土疲劳动三轴试验

1.1 基本物理指标

以兰州九州台黄土为研究对象，通过室内试验测得其基本物性指标，如表1所示。

表1 黄土基本物性指标

采用甘肃祁连山42.5#普通硅酸盐水泥按照3种配合比(3%、5%、7%)对黄土进行改良，通过击实试验得到不同水泥掺量的改良黄土最大干密度及最优含水率，如表2所示。

表2 水泥改良黄土基本指标

1.2 试验方案

试验主要研究围压及固结比对土样疲劳特性的影响。为模拟路基基床底层不同深度处土体的实际受力状态，使试验更具工程指导意义，文献[9]所述方法考虑轨道结构的重量以确定基床底层土体的围压及固结比范围，且据实测资料[10]表明，路基基床底层范围内土的侧向应力一般较小，以往相关学者对于该方面的研究大多针对大围压情况，与实际偏差较大，为更接近实际情况，经综合考虑，本次试验选取围压σ3为10 kPa、35 kPa和60 kPa，固结比KC(KC=σ1/σ3)为1、1.75、2.5。

采用压样器制备直径39.1 mm高80 mm的试样，标准养护28 d后进行试验，如图1所示。水泥掺量(下文以η表示)分别为3%、5%、7%；文献[11]中对列车荷载作用频率的描述，综合考虑设备条件及国内外研究经验，本次试验取加载频率为5 Hz。由于列车行驶时，不会在路基中产生拉应力，所以采用仅有压半周的半正弦波模拟动应力。通过GDS动三轴仪进行疲劳动三轴试验，如图2所示。获得水泥改良黄土疲劳动剪应变门槛以及临界动应力。

图1 试验所用土样

图2 GDS动三轴系统

1.3 试验步骤

安装试样，选择标准三轴试验下的CU模块，进行反压饱和；通过控制最大压力达到试验所需固结比的要求，等压固结的稳定标准为1 h内固结排水量变化不大于0.1 cm3，非等压固结标准为5 min内轴向变形大于0.005 mm；关闭排水阀，施加第一级轴向动应力σd1，频率取为5 Hz，振次取10 000次以上，仪器自动测记轴向动应变幅值εd1；振动完成后，卸除第一级轴向动应力σd1，打开排水阀，在固结应力作用下静置一段时间，使土样结构得到充分恢复；关闭排水阀，施加下一级轴向动应力(动应力的大小随试验的进行逐步调整)，如此循环直至试样破坏。

试验中试样所受应力随时间的变化曲线，如图3所示。竖向总应变随时间的变化曲线，如图4所示。图中OA为施加围压σ3阶段，BC为继续施加偏压(σ1-σ3)阶段，DE段为施加动应力σd阶段。εa为偏压固结

图3 应力随时间的变化曲线

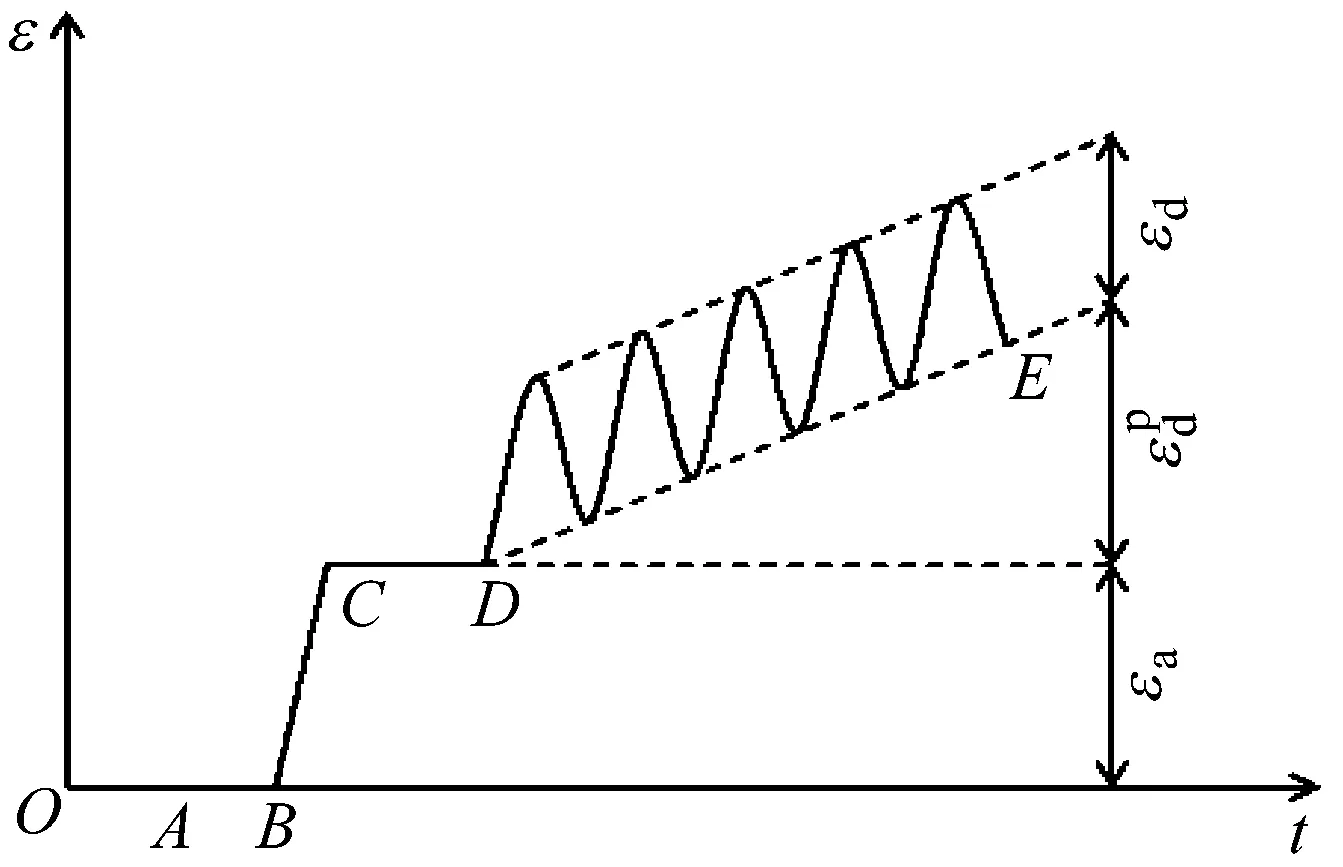
图4 应变随时间的变化曲线

2 试验结果分析

2.1 疲劳动剪应变门槛

疲劳动剪应变门槛是在反复循环荷载作用下，土体动刚度开始明显减小时所对应的动剪应变幅值，以此反映土体的长期动力稳定性。

2.1.1 疲劳动剪应变门槛的确定

为确定疲劳动剪应变门槛，结合水泥改良黄土疲劳动三轴试验结果，计算动模量Ed=σd/εd，采用Ed-σd曲线来确定疲劳门槛动模量EdL，进一步计算疲劳动剪应变门槛γtvL。通过Ed-σd曲线确定疲劳动剪应变门槛的具体方法如下：

(1) 每振动1 000次计算一个动弹性模量，每级荷载取10个数据点，将动弹性模量的平均值作为此级应力水平σd下的动弹性模量Ed，绘制如图5所示的Ed-σd曲线；

(a) 固结比KC=1

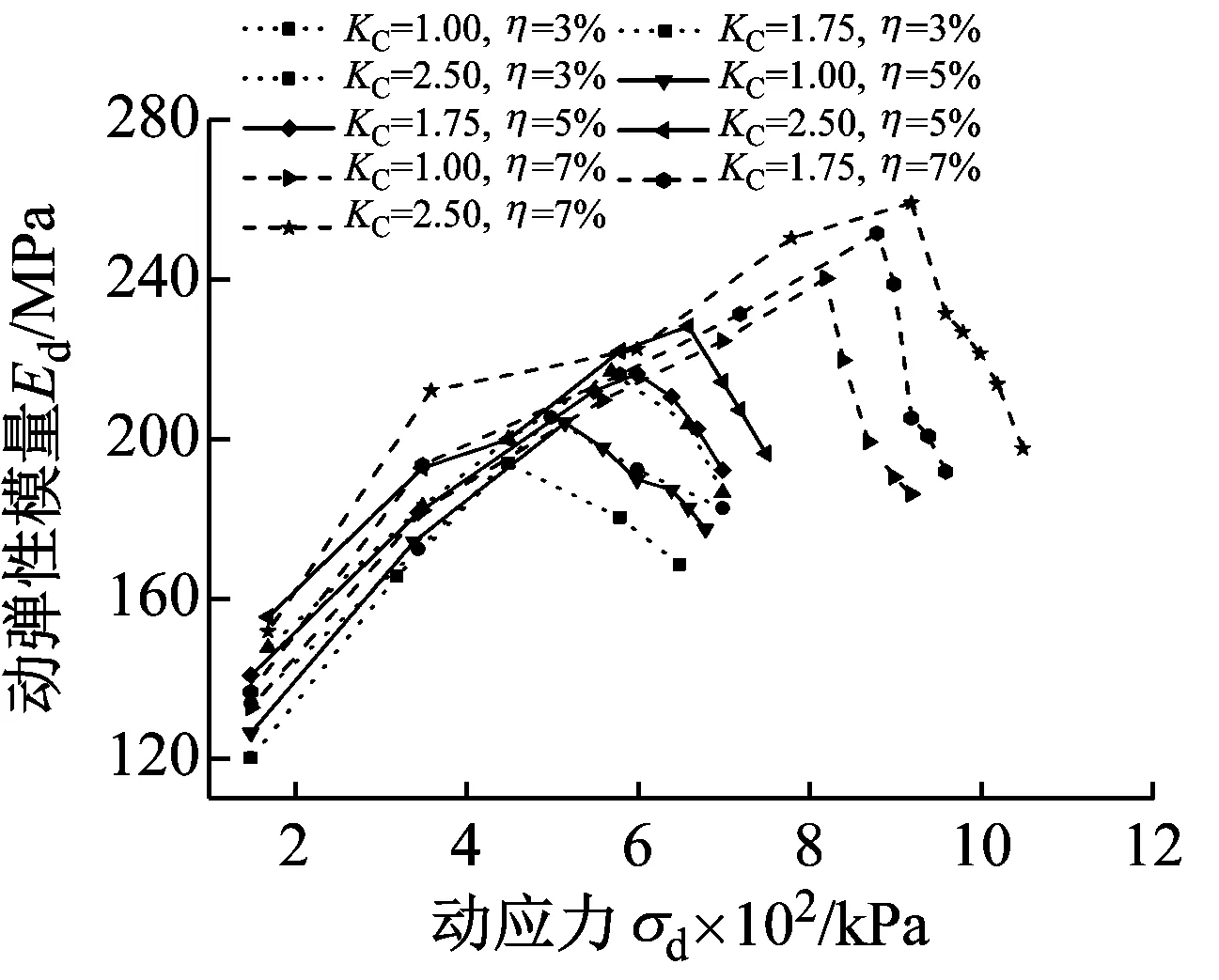
(b) 围压σ3=10 kPa

(2) 由图5可知，各试验工况下随动应力σd的增加，动弹性模量Ed均呈先增加后减小的趋势。动弹性模量Ed增加，表明试样逐渐被压密，其抗压性能逐渐增强；当动弹性模量Ed达到最大值后，动应力σd继续增加，动弹性模量Ed呈减小的趋势，表明试样结构已受到较大的扰动，甚至破坏；

(3) 将峰值动弹性模量定义为疲劳门槛动模量EdL，相应的竖向动应力定义为疲劳门槛动应力σdL。按公式EdL=σdL/εdL，反算疲劳门槛动应变εdL；

(4) 设试样大主应变εd1=εdL，小主应变εd3=-0.5εdL，以[(εd1+εd3)/2,0]为圆心，以(εd1-εd3)/2为半径绘制应变莫尔圆，该莫尔圆的半径R=(εd1-εd3)/2即为最大剪应变，也就是疲劳动剪应变门槛γtvL。

以水泥掺量η=5%，围压σ3=10 kPa，KC=1时为例，由图5可得，其疲劳门槛动模量EdL=204.3 MPa，疲劳门槛动应力σdL=516 kPa，经计算可得其疲劳动剪应变门槛γtvL=1.90×10-3，在同一动应力水平下，动弹性模量Ed随围压和固结比的增大而增加。以水泥掺量为5%为例，当固结比为1，围压从10 kPa增加到60 kPa时，EdL从204.3 MPa增加到243.1 MPa，σdL从516 kPa增加到800 kPa，相应的疲劳动剪应变门槛由1.90×10-3增加到2.47×10-3。当围压为10 kPa，固结比从1增加到2.5时，EdL从204.3 MPa增加到228.5 MPa，σdL从516 kPa增大到660 kPa，疲劳动剪应变门槛从1.90×10-3增加到2.17×10-3。由于7%的水泥掺量改良土水泥含量的增加，土体更加密实，其动弹性模量整体上较5%时更大，相应的疲劳动应力门槛值也较大，相反，水泥掺量为3%时动弹性模量及疲劳动剪应变门槛整体较5%时小。

2.1.2 疲劳动剪应变门槛影响因素分析

由前述确定疲劳动剪应变门槛的方法，通过计算得到每种实验工况下的动剪应变门槛值；其随水泥掺量、围压及固结比的变化情况，如图6所示。

由图6可知，水泥改良土疲劳动剪应变门槛受水泥掺量、围压及固结比的影响较大，随着水泥掺量、围压及固结比的增大，疲劳动剪应变门槛呈近似线性增大；且由图6(a)、图6(b)、图6(c)中曲线整体斜率的大小可见，相比围压及固结比的影响，水泥掺量对疲劳动剪应变门槛的提高最为显著，围压的影响次之，固结比的影响最小；考虑三种因素对疲劳动剪应变门槛的影响，在进行路基填料的选择时，首先应合理选择水泥掺量，其次在路基设计及动力稳定性评价时，疲劳动剪应变门槛的取值一定要具体考虑各路段的工程地质条件，如基床土物理状态、基床的实际受力状况等，以达到安全经济的双重目的。

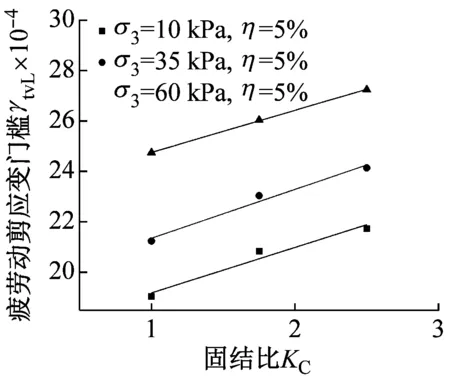
(a) γtvL随固结比KC的变化

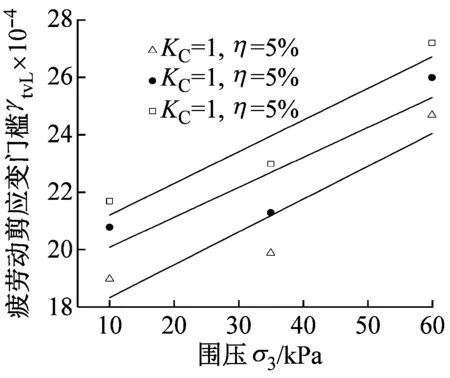
(b) γtvL随围压σ3的变化

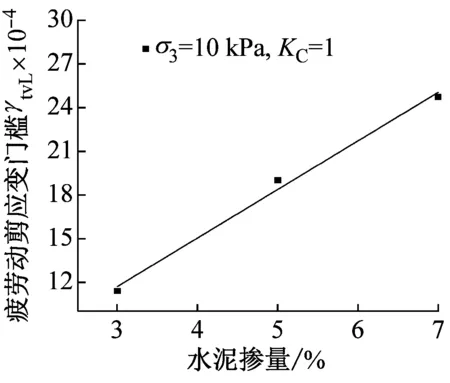
(c) γtvL随水泥掺量η的变化

图6 水泥掺量、围压及固结比对疲劳动剪应变门槛的影响

Fig.6 Influence of cement content, confining pressure and consolidation ratio on dynamic shear strain threshold of fatigue

2.2 临界动应力

2.2.1 临界动应力的确定及εp-lgN线型分析

临界动应力的确定通过εp-lgN曲线实现，将疲劳动三轴试验数据进行处理得到水泥改良黄土累积塑性应变εp随lgN的变化曲线，如图7所示，以水泥掺量为5%，σ3=10 kPa，KC=1为例对其εp-lgN曲线线型进行分析，以确定其临界动应力值。

由图7可知，随动荷载水平的增加水泥改良土的累积塑性应变逐渐增大，不同动应力水平下的εp-lgN曲线大致可以分为稳定型、临界型和破坏型三种。当动应力小于600 kPa时，曲线呈稳定型，即累积塑性变形在加载初期增加较明显，但随着试验的进行，土体呈现压密状态，试样基本处于弹性应变阶段，累积塑性变形趋于稳定；随着动荷载水平的增加，当动应力达到处于600～630 kPa时，其累积塑性变形随振次呈非线性增加的趋势，并不趋于稳定，称为临界型曲线；临界型介于稳定型与破坏型之间，将临界型所对应的轴向动应力作为临界动应力σdcr，理论上讲，特定试验工况下土的临界动应力为一固定值，但对于室内试验，临界动应力在某一个范围内变化，即这种实验工况下对应的临界动应力位于600～630 kPa。考虑工程实际及安全储备，暂取其下限值作为该工况下的临界动应力值以进行动力稳定性评价；当动应力超过630 kPa时，εp-lgN曲线转为破坏型，其特点是，随加载次数的增加，累积塑性变形急剧增大，试样发生脆性破坏；

图7 水泥改良黄土εp-lg N曲线

2.2.2 临界动应力影响因素分析

利用上述确定临界动应力的方法，得到不同水泥掺量、围压及固结比对临界动应力的影响如图8所示。

由图8可知，水泥改良黄土临界动应力值受水泥掺量、围压及固结比的影响明显；由图8(a)可知，随着固结比的增大，临界动应力呈近似线性增大，且增大幅度较小；由图8(b)可知，临界动应力随着围压的增大也逐渐增大，增加幅度较大，且围压越大，增加梯度越大；同样水泥掺量对临界动应力的影响最大，围压次之，固结比的影响最小；考虑围压对临界动应力的影响，在实际工程中应注意对基床部分的加固，因为基床部分土体围压较小，由上述研究成果可知，对应的的临界动应力也较小，而由动应力在路基中的衰减规律可知，列车在基床中产生的动应力却较大，故易产生较大变形。

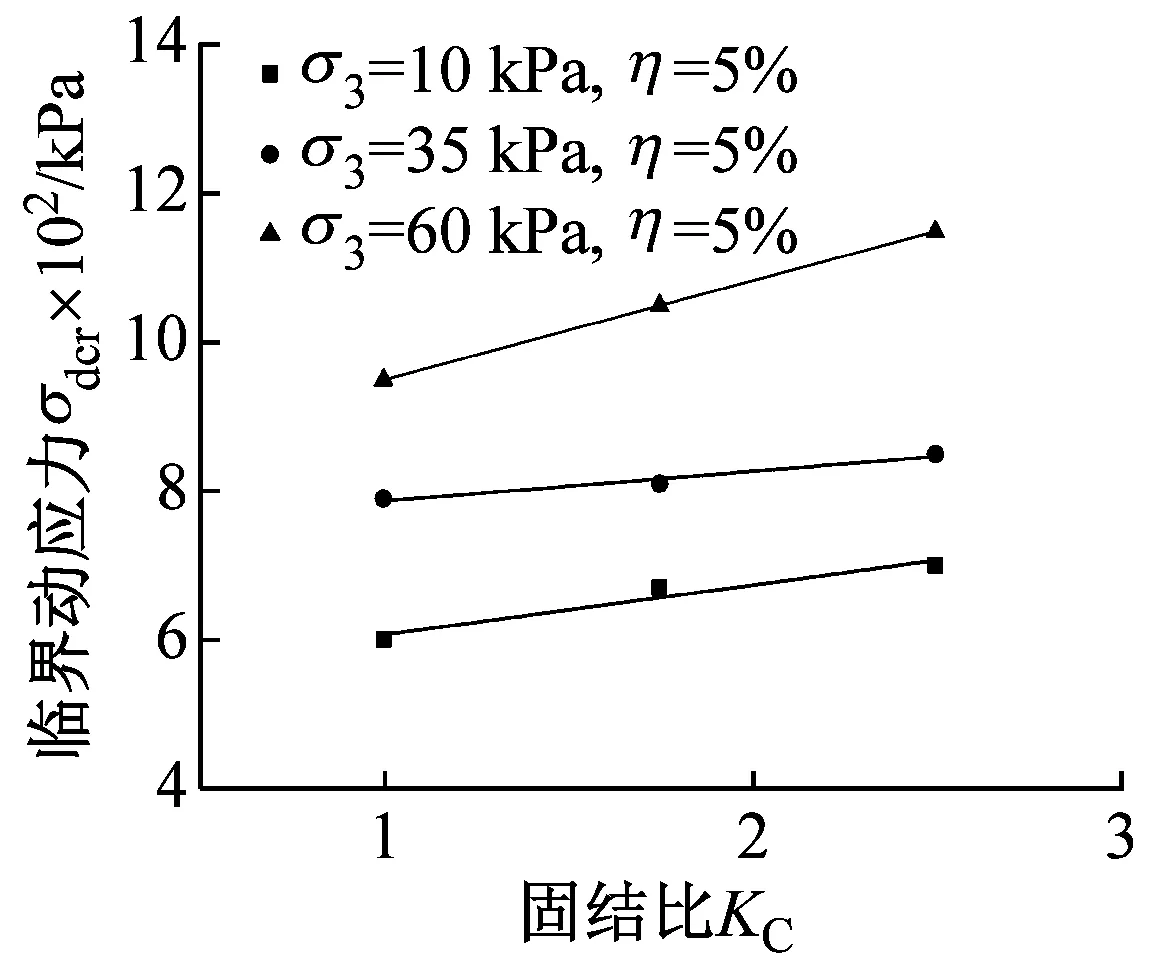
(a) σdcr随固结比KC的变化

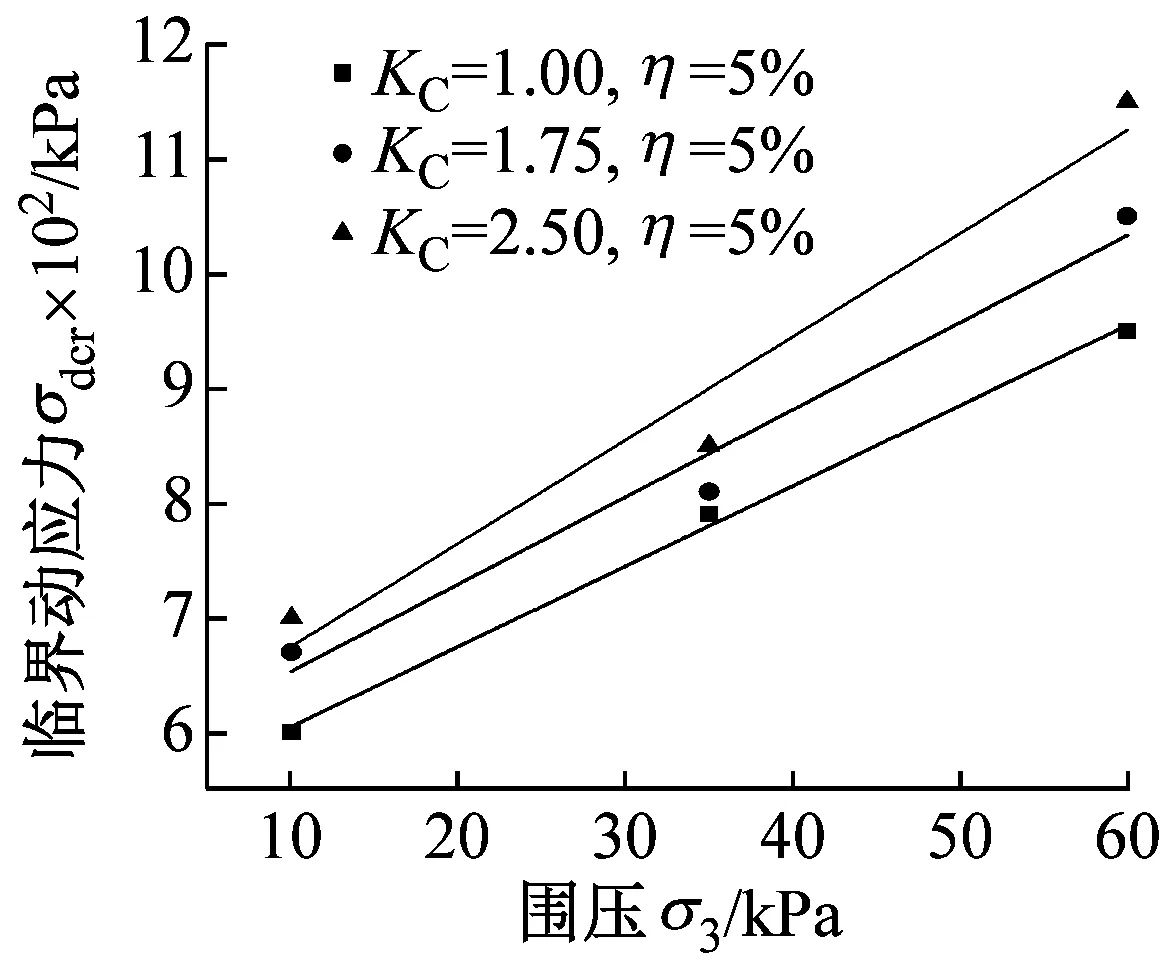
(b) σdcr随围压σ3的变化

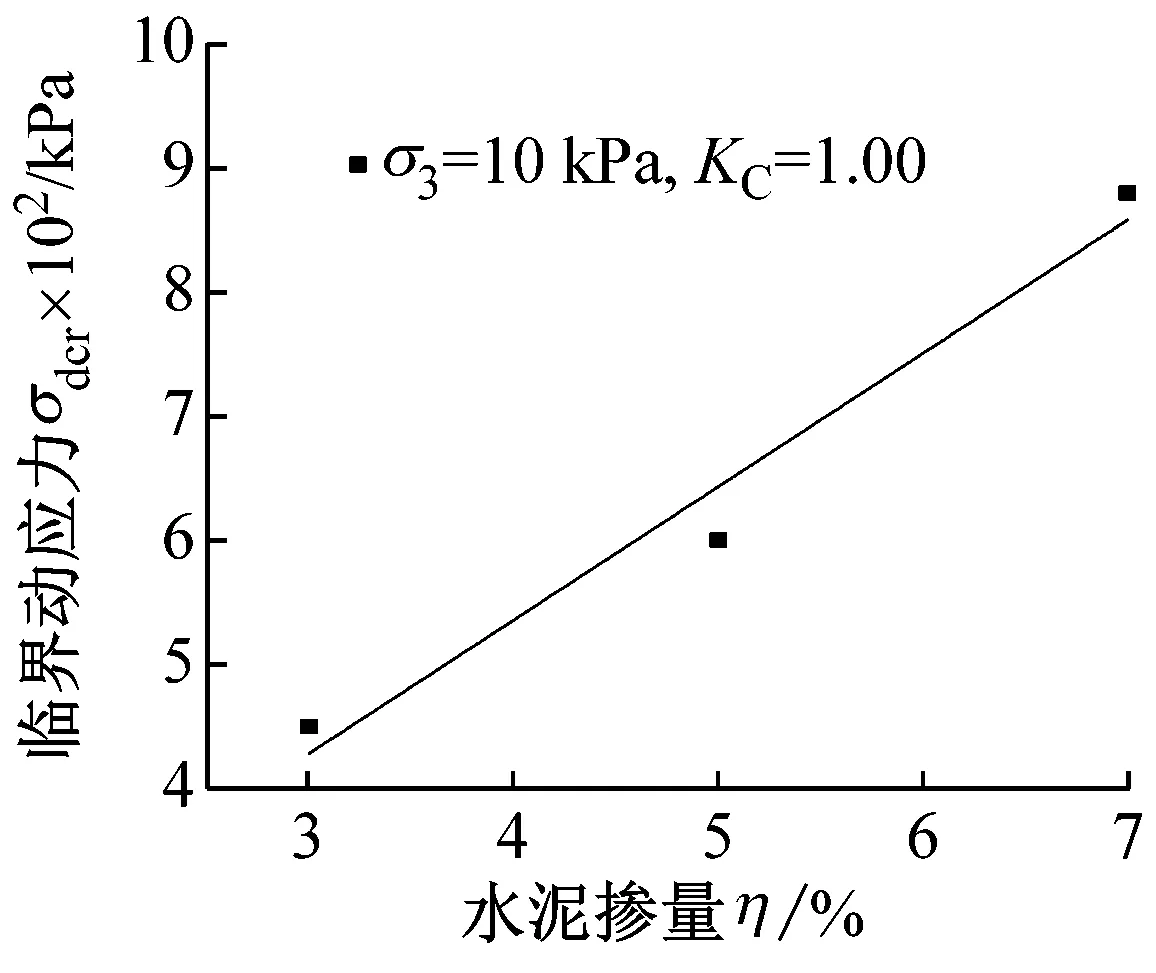
(c) σdcr随水泥掺量η的变化

图8 水泥掺量、围压及固结比对临界动应力的影响

Fig.8 Influence of cement content, confining pressure and consolidation ratio on critical dynamic stress

2.3 实验结果回归分析

各实验工况下水泥改良土疲劳动剪应变门槛及临界动应力下限详值，如表3所示。

考虑到采用疲劳动三轴试验确定疲劳动剪应变门槛及临界动应力较为繁杂，工作量大，为便于工程应用，基于不同试验条件下水泥改良黄土疲劳动剪应变门槛及临界动应力试验值，考虑不同水泥掺量，围压及固结比的影响，进行三元线性回归，获得了水泥改良黄土的动剪应变门槛值及临界动应力的经验估算公式如下所示。

γtvL=(3 177.78η+0.847σ3+18.07KC-1.82)×10-5R=0.984 4

(1)

σdcr=8 222.2η+6.622σ3+85.185KC+64.704

R=0.975 6

(2)

式中：η为水泥掺量，取3%、5%、7%；σ3为围压，单位 kPa；KC为固结比。

上式形式简单，参数易于获得，相关系数较高，就上述实验工况而言，计算值与表3所得试验值吻合较好，可为高速铁路水泥改良黄土路基设计及长期动力稳定性研究提供一定的参考。原则上该结果只在一定范围内适用(3%≤η≤7%，10≤σ3≤60，1≤KC≤2.5)，但其可为类似问题提供一定参考。

3 路基长期动力稳定性评价

分别选取基床底层表面、中部、底部三个具有代表性部位来对比分析，参照文献[9]的计算方法，将基床不同深度土体的应力状态等效于本次实验各参数取值范围内，即不同深度处土体对应的围压及固结比，如表4所示，进而利用经验估算式(1)和式(2)计算不同围压及固结比所对应的深度处土体的疲劳动剪应变门槛及临界动应力，与实际动剪应变及动应力进行对比分析。

3.1 动剪应变法

动剪应变法评判条件[12]为：当基床某深度Z处动剪应变γdz小于疲劳动剪应变门槛γtvL即满足γdz<γtvL时，基床是长期稳定的。

根据剪切波传播理论，不同深度处动剪应变γdz[13]可由式(3)、式(4)、式(5)计算得到。

γdz=Vres,eff,z/Cs

(3)

Vres,eff,z=Vres,eff,SUe-0.2Z

(4)

Vres,eff,SU=0.2e0.011Vzug

(5)

式中：Vres,eff,z为有效振速；Vres,eff,SU为路基面处有效振速；Z为土体深度；Cs为土体的剪切波速；Vzug为列车行驶速度。

表3 水泥改良黄土疲劳动剪应变门槛及临界动应力

Tab.3 Fatigue dynamic shear strain threshold and critical dynamic stress of cement-improved loess

实验序号水泥掺量/%围压/kPa固结比疲劳动剪应变门槛×10-3临界动应力/kPa12345678910111213141516171819202122232425262735710356010356010356011.144101.751.315002.51.4760011.306801.751.457102.51.6073011.548201.751.718802.51.8597011.906001.752.086702.52.1770012.127901.752.308102.52.4185012.479501.752.6010502.52.72115012.478801.752.629202.52.6699012.659701.752.7810102.52.89106012.7810401.752.9211202.53.041210

表4 稳定性评价选取参数

路基面处总有效振速Vres,eff,su可按两种方法综合确定：①按式(5)计算，列车行驶速度取Vzug=350 km/h，Vres,eff,SU=0.2e0.011×350=9.4 mm/s；②根据规范推荐值[14]确定。按最不利因素考虑，取Vres,eff,su=15 mm/s。综合考虑按最不利情况，取Vres,eff,su=15 mm/s。

根据文献[15]，黄土剪切波速范围为130～300 m/s，考虑土层结构在动载作用下被扰动，其剪切波速将随土体结构的扰动而减小，因此取值时将实测剪切波速适当降低，故该处剪切波速取100～250 m/s，由于水泥改良土其密实程度较高，剪切波速较素黄土大，故取黄土的剪切波速计算是偏于安全的。

考虑最不利情况，取剪切波速下限即100 m/s，故不同深度处动剪应变

γdz=Vres,eff,z/Cs=15×10-3×e-0.2Z/100

将不同水泥掺量时不同深度土体的动剪应变门槛值与实际动剪应变值进行对比分析，结果如表5所示。

表5 基床不同深度动剪应变法对比结果

Tab.5 Contrast results with dynamic shear strain method at different depths of subgrade bed

水泥掺量/%深度/m动剪应变γdz×10-5动剪应变门槛γtvl×10-33570.413.851.381.5511.01.452.78.741.540.413.852.021.5511.02.092.78.742.180.413.852.651.5511.02.722.78.742.82

由表5可知，基床底层动剪应变值随深度的增加逐渐衰减，顶面处的动剪应变值最大，为1.385×10-4，而与此处对应的3%的水泥改良土疲劳动剪应变门槛γtvL为1.38×10-3，为该处动剪应变的10倍。根据文献[12]，当γd<γtvL时，路基土体处于线弹性工作状态，满足长期动力稳定性的要求，且不需要验证附加沉降是否满足要求；则由对比分析结果可知，不同水泥掺量的改良黄土不同深度的动剪应变值均小于疲劳动剪应变门槛，且距动剪应变门槛存在较大距离，均能满足路基长期动力稳定性要求，鉴于工程实际中通常采用水泥掺量为5%，并考虑到足够的安全储备、高标准的优质路基的实现以及经济效应，建议水泥掺量控制在约5%。

3.2 临界动应力法

当路基填料的临界动应力小于列车动荷载产生的动响应时，在列车动荷载往复作用下，会导致土体结构破坏失稳，强度降低，变形迅速增大，直至破坏。当临界动应力大于列车动荷载传递到水泥改良土时的动应力时，在动荷载作用下，土体被逐渐压密，应变增量逐渐减少，当加载到一定次数时，土体密度达到一定程度。因此，实际动应力小于临界动应力，基床是长期动力稳定的。

对于高速铁路无砟轨道路基中列车荷载作用下的动应力沿深度的分布特性，相关学者曾通过现场实测及数值计算的方法开展了很多的研究，部分研究成果[16-20]如图9所示。由图9可知，无砟轨道不同轨道结构形式、路基结构形式、综合检测列车类型及重车类型情况下基床动应力最大值小于20 kPa，而由式(2)计算可得，5%水泥掺量的基床表层土体临界动应力为713 kPa，远大于路基中实际最大动应力，故以水泥改良黄土作为路基基床底层填料，从动强度角度来说，满足长期动力稳定性要求，且安全性得到很大保障。

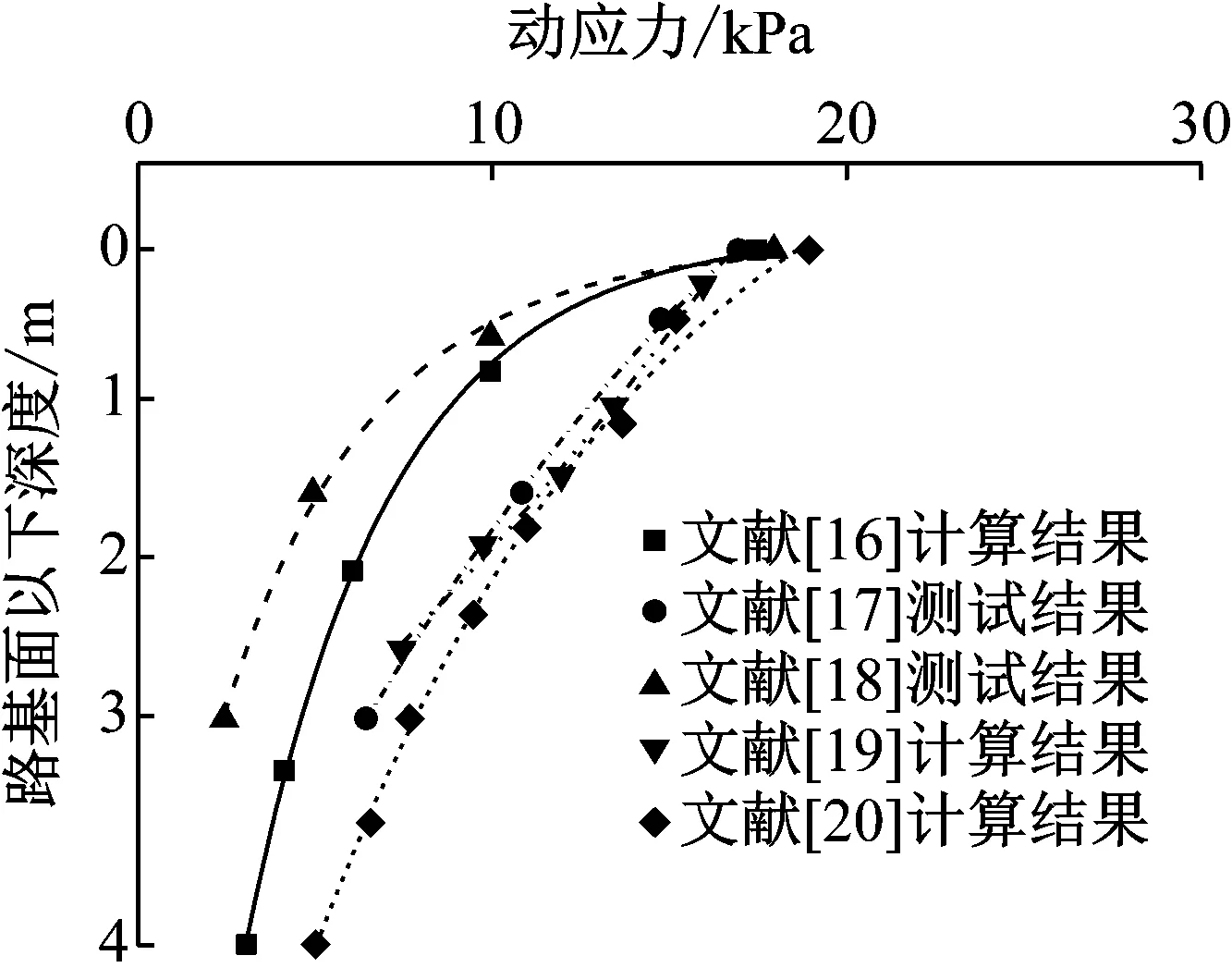
图9 无砟轨道路基动应力沿深度衰减曲线

从上述两种评价方法的对比结果来看，三种水泥掺量改良土均可满足高速铁路路基长期动力稳定性要求，动剪应变法评价结果显示，3%基床底层表面处土体的疲劳动剪应变门槛是该处动剪应变的10倍，而采用临界动应力法时，此处土样的临界动应力与现场实际动应力相差甚远，故只采用动应力来对路基长期动力稳定性进行评价时路基长期动力稳定性难以保证，临界动应力法只是从动强度角度对长期稳定性进行评价，未考虑到动变形的影响，鉴于高速铁路对变形的严格要求，故其评价结果值得商榷；另一方面，从土样受到循环荷载以后性状改变的过程来看，必然是刚度的降低引起变形的增长，从疲劳门槛动应力与临界动应力的大小亦可得出，即土体在满足临界动应力的要求，未达到强度破坏前，可能变形要求已不满足，故采用动剪应变法较临界动应力法要求更高，结果更加准确，即评价效果更佳。

4 结 论

通过疲劳动三轴试验对水泥改良黄土的疲劳特性进行了研究，探讨了不同水泥掺量、围压及固结比对疲劳动剪应变门槛及临界动应力的影响，并对水泥改良黄土作为基床底层填料时路基的长期动力稳定性进行了评价。主要得到以下结论。

(1) 水泥改良黄土动弹性模量随动应力的增加呈现出先增大后减小的趋势；可通过Ed-σd曲线来确定其动剪应变门槛；而εp-lgN曲线按走势可分为稳定性、破坏形以及临界型。

(2) 随水泥掺量、围压及固结比的增加，水泥改良黄土疲劳动剪应变门槛及临界动应力显著增大，且水泥掺量对其影响最大，围压次之，固结比的影响最小。

(3) 考虑水泥掺量、围压及固结比对其疲劳特性的影响，在进行路基填料的选择时，应合理选择水泥掺量，且动剪应变门槛及临界动应力的取值一定要具体考虑各路段的工程地质条件，如基床土物理状态、基床的实际受力状况等，以达到安全经济的双重目的。

(4) 当以三种水泥掺量的改良黄土作为路基基床底层填料时，均能满足路基长期动力稳定性要求。综合考虑建议水泥掺量控制在约5%。

(5) 对路基长期动力稳定性进行评价时，相比临界动应力法，动剪应变法是一种更加系统，更加全面的评价方法。