对一道中考试题的深度思考

(岭南中学，上海 200435)

笔者拜读了文献[1]后受益匪浅，特别敬佩黄老师对“一线三等角”模型的深度挖掘能力与得心应手的应用技巧．透过现象看本质，笔者有几点不同的拙见，现不揣浅陋略作分享，以求抛砖引玉．

1 题目及其解法的新解读

题目如图1，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，联结AC，若AC=6，则四边形ABCD的面积为______．

(2017年陕西省数学中考试题第14题)

图1 图2

这是一道普通的求不规则四边形的面积问题.基本思路就是通过割补转化成三角形或规则四边形求解，而联结对角线把不规则四边形分成两个三角形求其面积是最常见的转化策略．由AC=6自然想到分别过点B，D作BE⊥AC于点E，DF⊥AC于点F(如图2)，则

从而问题就转化成求BE与DF的长了．求BE的长主要有两种方法：1)解直角三角形；2)利用与已知线段间的数量关系.但无论是在Rt△ABE还是在Rt△CBE中，都无法通过解直角三角形直接求出BE的长，于是解题思路就转向寻求所求线段BE与已知线段AC间的数量关系．虽然易证△ABE≌△DAF，得BE=AF，但并不能找到两者间确切的数量关系，转而想到整体求BE+DF的值．又易猜想BE+DF=AC，因此问题最终定位在如何证明DF=CF．注意到∠DFC=90°，自然想到证明∠DCF=45°．可是，图2中与∠DCF相等的45°角又在哪里呢？由AB=AD和∠BAD=90°想到联结BD，由∠BAD+∠BCD=180°可知点A，B，C，D共圆，从而∠DCF=∠ABD=45°，问题迎刃而解．由此可见,图2的辅助线生成是基于如何求三角形的面积(运用面积公式处理)，而非源于所谓的“一线三等角”模型．

当然也可考虑分别以BC，CD为底边构造高，即分别过点A作AM⊥BC于点M，AN⊥CD于点N(如图3).可知

∠ACD=∠ACB=45°，

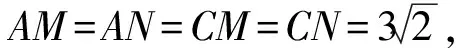
于是S四边形ABCD=S△ABC+S△ACD=

易证△ABM≌△AND，得BM=DN，则

可求得四边形ABCD的面积为18．

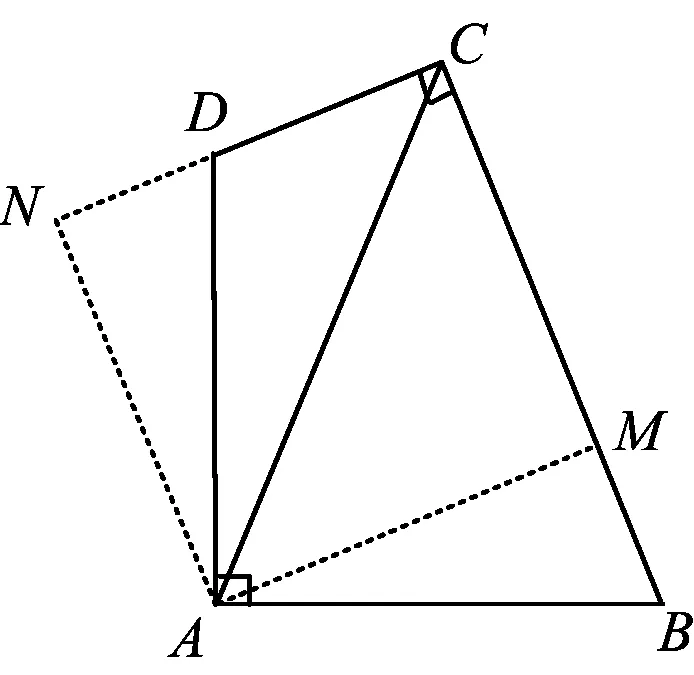
图3

在图3中，既然△ABM与△AND始终全等，那么在确保∠BCD为直角且长为6的AC平分∠BCD的前提下，把直角∠BAD绕着点A旋转任意角度后，所得的四边形均符合题意，即AB=AD．也就是说点B可以在射线CM上任意运动(点D也就随之在射线CN上运动)，所得四边形虽形状不同但面积始终不变．既然CB的长短可随意变化，那么图2中BE与DF的大小也就不为定值，故欲求四边形ABCD的面积也只能着眼于整体，求BE与DF之和了．

另外，若分别以AB，AD为底边构造高又如何呢？如图4，分别过点C作CP⊥AB于点P，CQ⊥AD于点Q，则

图4

由前面的分析可知AB，AP与CP的大小也是在不断变化的，不是确定的值，因此如何引入一个适当的参数并表示出这3条线段，再消参数求面积便是解题的思考方向了．由AC=6和∠ACB=45°想到设∠ACP=α，则

AP=6sinα，CP=6cosα，

BP=6cosαtan(45°-α)，

于是AB=6sinα+6cosαtan(45°-α)=

化简过程要用到两角差的正切公式与“切割化弦”，代入可得四边形ABCD的面积为18．

既然点B的位置可以在射线CM上不断变化，那么由图3可知，当点B运动到点M位置时四边形ABCD就成为以AC为对角线的正方形，求其面积自然也就轻而易举了．由此可得一个新的解题思路，直接把△ABM割补到△ADN的位置(即把△ABM绕点A逆时针旋转90°)，由∠ADC+∠B=180°可证点C，D，N共线，从而把四边形ABCD的面积转化为正方形AMCN的面积，进而得到四边形ABCD的面积为18．

顺延运动的思路，显然当点B运动到点C处时，四边形ABCD的面积就变成了等腰Rt△ACM的面积(如图5).而从割补角度来看，图5就是把△ABC绕点A逆时针旋转90°到△ADM的位置(即把△ABC割补到△ADM的位置)，由于∠ADM+∠ADC=∠B+∠ADC=180°，因此点A,D,M共线，从而

S四边形ABCD=S△ADC+S△ADM=S△ACM=18.

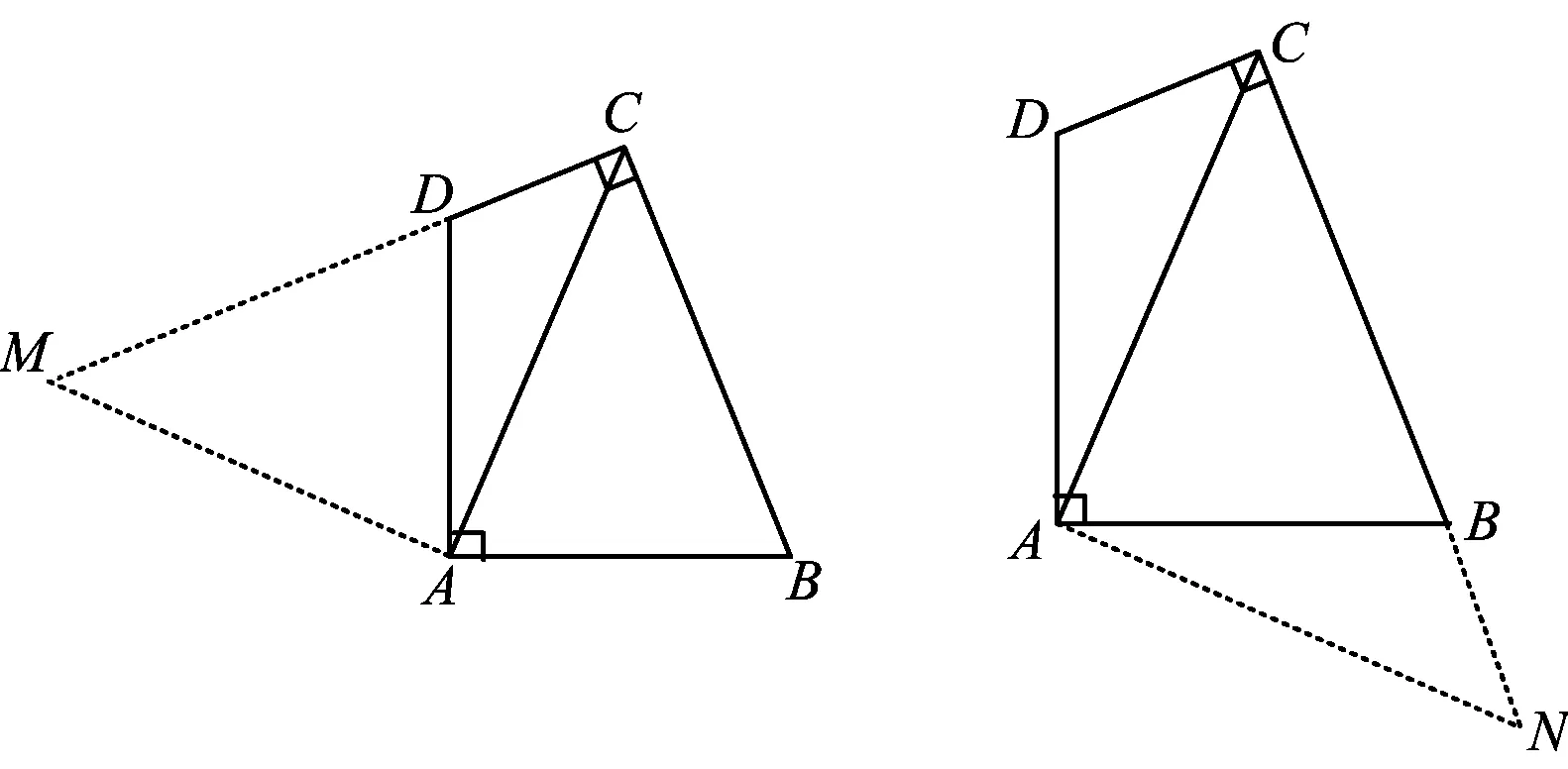
图5 图6

当然也可把△ACD绕点A顺时针旋转90°到△ABN位置(如图6)，同样可求得四边形ABCD的面积为18．

文献[1]从构造“一线三等角”模型入手提供了如图7所示的辅助线添法，即过点C作EF⊥AC，分别交AD,AB的延长线于点E,F，由∠BCD=90°想到再分别过点B,D作BH⊥EF,DG⊥EF，垂足为点H,G，从而构造出“一线三等角”模型，并引入∠CAB=α(参数)求出四边形ABCD的面积(具体过程请参考文献[1]思路5)．对图7的辅助线生成，笔者认为是基于“补形”，即把不规则的四边形补成三角形(之所以作AC的垂线是因为构造直角三角形计算方便)，从而把四边形ABCD的面积转化成△AEF与△CDE,△CBF的面积之差．对于求两个非直角三角形(△CDE与△CBF)的面积，理所当然要作高，而CE,CF又易用参数α表示，故以其为底边构造高就是必然之举了．由此可见，所构造出的“一线三等角”模型纯属巧合，并非刻意而为，更不是辅助线的生长点．

图7 图8

既然“补形”，而∠BAD又为直角，不妨直接延长AD,BC交于点T，构造Rt△ABT(如图8)，则四边形ABCD的面积就转化为△ABT与△CDT的面积之差．由条件AC=6和∠ACB=45°想到过点A作AS⊥BC于点S，则

显然△ABT与△CDT的面积也不是定值，因此需引入参数表示．注意到∠TDC=∠TAS=∠B，故可设其大小为β，则

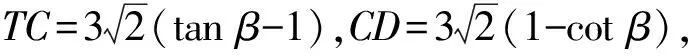
S四边形ABCD=S△ABT-S△CDT=

当然，也可补成如图9所示的Rt△BCK求解(略)．

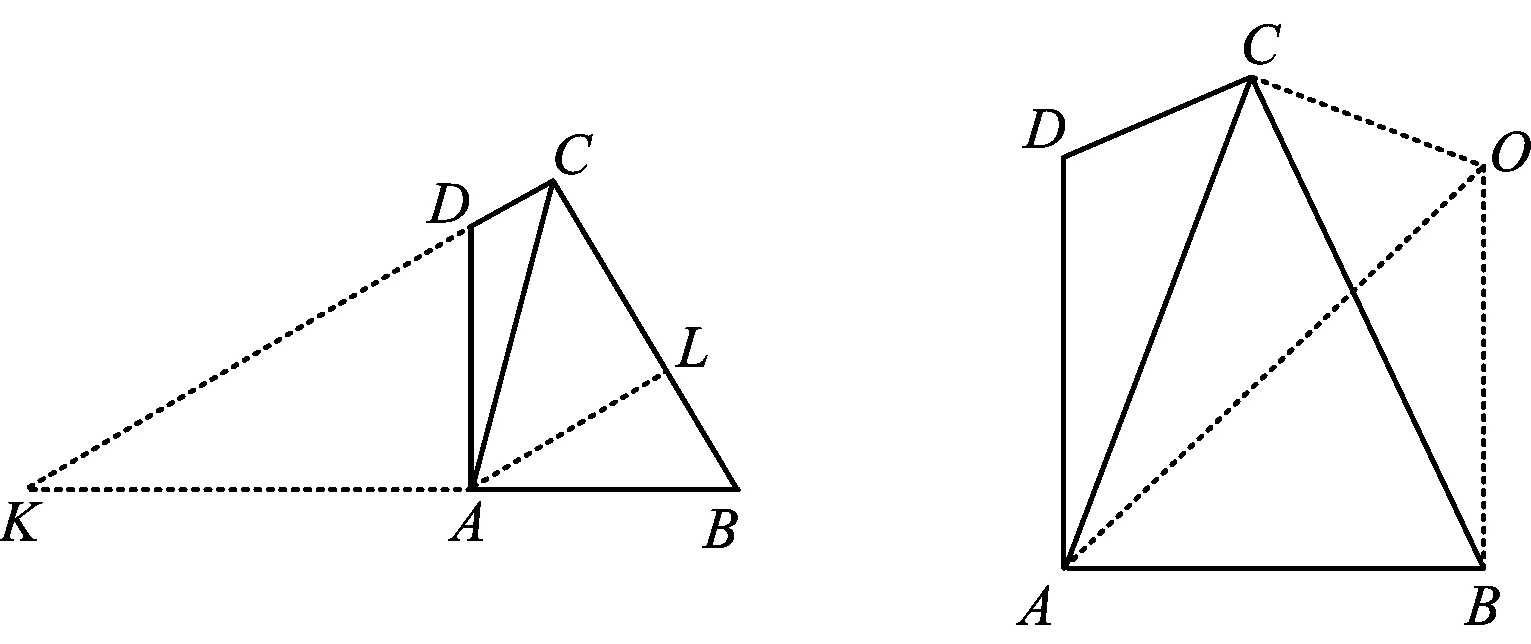
图9 图10

有趣的是，把四边形ABCD分成△ABC和△ACD后，用三角形的正弦面积公式求解还有别有洞天之感．不妨设∠BAC=θ，则

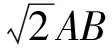
由∠ACB=∠AOB=45°，知点A,B,C,O共圆，则

∠ACO+∠ABO=180°，

进而得∠ACO=90°，问题迎刃而解．

通过以上分析不难看出，各辅助线的生成主要源于运用“割补法”的转化策略和求三角形面积的基本方法，与构造“一线三等角”模型几乎没有关联．

2 两点思考

2.1 通性通法应源于问题的本质

正如文献[1]所言:通性通法是解决某类问题最合理的想法、最基本的思路、最普遍的操作程序．但就求不规则的四边形面积而言，利用“分”“割”“补”把四边形转化为规则图形求解才是处理此类问题的通性通法，也是辅助线生成的本源．纵然构图中出现了“一线三等角”模型，那也是无心插柳之举，绝非添辅助线的突破口，若刻意为之，则可能会弄巧成拙．如文献[1]为了突出所谓的“一线三等角”模型，选择了图形最复杂、计算最繁琐的补形方法(见文献[1]中的图10)，与本文中的图8、图9相比，似乎有捡了芝麻丢了西瓜之嫌．对比两篇文章的思路剖析也不难看出，文献[1]从构造“一线三等角”模型入手解读辅助线的生成只抓住了表象，并未切入问题的本质，甚至束缚了思维，错过本文中不少简捷而又不失精彩的证法，难免有进了宝山却空手而归之憾．总之，本中考题思维的着力点应放在如何求不规则的图形面积上，而非苦思冥想去构造所谓的“一线三等角”模型．

2.2 “模型化”解题教学应把握好度

毋庸讳言，最近比较流行的“模型化”教学确实丰富了学生的解题技巧，为解决问题开辟了一条快捷通道，甚至在一定程度上打开了解题思维的又一扇窗，但过于夸大“模型”的功能，甚至教学生“死套”就值得商榷了．对此笔者有3个建议：首先，构建“模型”要理清来龙去脉．建模时一定要突出过程化教学，引导学生发现“模型”，深入挖掘“模型”背后所折射的本质．如“一线三等角”模型实际上就是依据“三角形的外角等于两个不相邻的内角和(或两个相邻小角组成的大角等于另外两个不同位置的角之和)”得到两个三角形相似(含全等)，进而利用相似三角形的性质解决问题．掌握这一本质方能不为其表象所惑，具体运用时也能更加得心应手．其次，运用“模型”要讲究水到渠成．运用“一线三等角”模型解题时切忌过于执著，而要顺势而为，否则就会弄巧成拙．若一直线的同侧恰有3个等角，运用模型就是信手拈来之事；若一直线的同侧已有两个等角，则再构造第3个等角也许能恰到好处，甚至柳暗花明．最后,收集“模型”要善于去伪存真．最近流行的模型比较多，除了文献[1]中所提的“一线三等角”模型外，还有“将军饮马”“共线短路(平面内一点与圆上各点连线中，当动点、定点与圆心这3个点共线时最短)”“旋半角(大角中含有共顶点的半角可通过旋转转化)”“手拉手(两个共一顶点的相似三角形，本质是放缩旋转)”等模型，令人目不暇接．但其中难免鱼龙混杂，甚至顾其名都难思其义，只不过是为一些基本图形冠以一个哗众取宠的名字而已，不值得细细推敲．收集时切忌来者不拒，甚至全力向学生“倾销”，以致捡了芝麻丢了西瓜，犯教学之大忌也！

总之，“模型化”解题只是一种技巧，有其一定的积极意义，但绝非“通性通法”，与六大核心素养之“数学建模”也有天壤之别．实际运用中切不可过分推崇，否则就可能会因一叶障目而舍本逐末了．